无定向附合导线测量方法探讨
2023-02-05胡海斌余广勤郭新慧
胡海斌,余广勤,郭新慧
(1.山西工程科技职业大学,山西晋中 030619;2. 山西四建集团有限公司,山西太原 030012;3.山西省测绘地理信息院,山西太原 030001)
0 引言
在城市工程建设中,在一些特殊的场景中利用全站仪进行导线点坐标测量仍被广泛应用。通常导线测量要求具有高精度且满足通视条件的起算数据,但在实际测量工作中常遇到导线点被人为破坏或已知导线点由于工程建设通视条件被破坏,导致无法按照常规的作业方法进行坐标测量。无定向附合导线是导线两端点为已知坐标起算点而没有起算方位角的导线[1]。通常已知点间不能直接通视时布测无定向导线是非常有利的。在边长不太长时(如1 km 以内),采取一定措施,可以获得较高的精度[2]。因此,在施测区域内,如果仅有两个互不通视的埋设完好的高精度导线点,可以利用这两个已知导线点建立一条无定向附合导线,以解决导线起算数据不足的问题,重建更多导线点,满足地形图修补测图和施工放样的需要。文献[1]对无定向边附合导线法的施测计算、精度分析和适用条件等方面进行了探讨;文献[3]对无定向附合导向的计算原理和程序设计进行了研究;文献[4]对无定向附合导线的应用、两种平差计算的方法及精度进行了分析。目前无定向附合导线测量方法虽然精度上可以满足工程建设的需求,但还存在测量效率不高的问题。针对此问题,本文对无定向附合导线常规测量方法进行了简化处理,并结合实例进行验证分析,简化方法在保证精度的前提下可体现效率提升的优越性。
1 无定向坐标附合导线测量方法
1.1 常规测量方法
A、B为已知点,1、2、…、n为未知点,S1、S2、…、Sn+1为观测边长,β1、β2、…βn为观测转折角。无定向附合导线的观测角比观测边长少一个,已知量也少两个起、闭方位角,因此在坐标计算中,必须采取假定起始方位角,即假定坐标系的方法[3]。如图1 所示。

图1 无定向附合导线
1.1.1 基本思路
假设某无定向附合导线为A-1-2-B,其中已知导线点A和B互不通视,点1 和2 为未知导线点。如图2 所示。

图2 无定向附合导线:A-1-2-B
为了测定1 点和2 点的坐标,一般采取以下思路:
1)建立假定坐标系统。
由于无定向附合导线在获取未知点坐标时缺乏起始边方位角,无定向附合导线无法直接测定原有的XOY测量坐标系下的1 点和2 点的精确坐标,首先需要假定一个M O′N坐标系统。
2)利用外业测角测距确定假定坐标系下的各点坐标。
3)将各点假定坐标通过旋转、平移、缩放等过程转换成测量坐标下的坐标。
1.1.2 具体实施步骤
假定A点(O′点)为原点,A1 边方向为纵轴方向,以A1 边垂直方向为横轴方向,建立M O′N假定坐标系统。在M O′N假定坐标系统中,A点(O′点)的坐标为(0 m,0 m),A1 边的坐标方位角αA1为0°00′00″,如图3 所示。
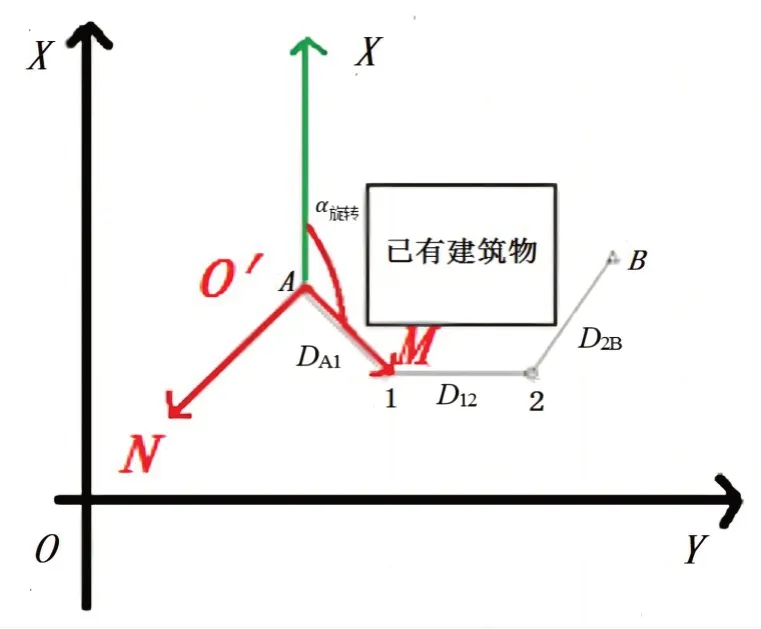
图3 测量坐标系统和假定坐标系统
全站仪导线测量一般需要观测转折角和每条折线的水平距离。
1)用全站仪依次观测导线左角∠A12、∠12B各两个测回并取平均值。
2)用全站仪依次往测相邻两点之间的水平距离DA1、D12、D2B各两个测回并取平均值。
3)利用方位角左角公式计算12 边、2B边的坐标方位角α12、α2B。
4)利用坐标正算公式,计算假定坐标系下的1点、2 点、B点坐标。
5)旋转处理和假定坐标方位角。
①计算旋转方位角α旋转
旋转方位角是指原有测量坐标系指北方向顺时针转至假定坐标系指北方向的方位角。
经过外业施测得到假定坐标系下各点坐标后,由于A点、B点既有原来测量坐标系下的已知坐标,又有假定坐标系下的假定坐标。因此可以通过坐标反算公式计算AB边的已知坐标方位角α已知和假定坐标方位角α假定,计算旋转方位角,如式(1)所示:
需要注意的是,若α旋转>360°,则需自动减去360°;若α旋转<0°,则需自动加上360°。
②依次计算测量坐标系下的各边坐标方位角αA1、α12、α2B,比如αA1公式如式(2)所示:
需要注意的是,各边坐标方位角旋转计算后,需注意是否与测量坐标系下实际所在象限一致,若不一致,需进行一致性处理。
6)平移处理。
利用计算出的测量坐标系下的各边坐标方位角以及实测的各边水平距离,计算1、2、B点平移后的坐标,比如1 点平移后坐标公式为:
若XB平移与XB已知不一致,YB平移与YB已知不一致,则说明经过平移计算后,还存在坐标闭合差。
X轴方向上的坐标增量闭合差为:δx=XB平移-XB已知,Y轴方向上的坐标增量闭合差为:δy=YB平移-YB已知。
根据精度要求,还需计算坐标增量闭合差v△xi、v△yi,对1、2、B点平移后的坐标进行改正,比如1点平移后的坐标改正数以及改正后坐标公式如式(4)、(5)所示:
7)缩放处理。
若经过平移处理后,若XB改与XB已知仍然不一致,YB改与YB已知仍然不一致,则说明经过平移处理后,还需要缩放处理。
X轴方向上的缩放系数计算公式如式(6)所示:
Y轴方向上的缩放系数计算公式如式(7)所示:
计算经缩放处理后和2 点的坐标,比如1 点公式如式(8)所示:
经过旋转、平移和缩放处理后,各点假定坐标系下坐标可以精确转换至原来测量坐标系下坐标。
1.2 简化方法
上述常规方法不管是外业施测还是内业数据处理,均需要花费较长时间。由于全站仪还可以直接观测坐标,为了发挥全站仪自身优势,还可以尝试直接观测未知点坐标两个测回取平均值的方法,同时借鉴施工坐标系与测图坐标系坐标转换公式直接转换坐标,从而提高观测效率。
1.2.1 基本思路
仍然以如图2 所示的无定向附合导线A-1-2-B为例,简化方法思路如下:
1)建立假定坐标系统
由于无定向附合导线在获取未知点坐标时缺乏起始边方位角,无定向附合导线无法直接测定原有的XOY测量坐标系下的1 点和2 点的精确坐标,首先需要假定一个M O′N坐标系统。
2)利用外业直接观测坐标确定假定坐标系下的各点坐标。
3)将各点假定坐标直接通过坐标转换公式转换成测量坐标下的坐标。
1.2.2 具体实施步骤
假定A点(O′点)为原点,A1 边方向为M轴方向,以A1 边垂直方向为N轴方向,建立M O′N假定坐标系统。在MO′N假定坐标系统中,A点(O′点)的坐标为(0 m,0 m),A1 边的坐标方位角αA1为0°00′00″。
1)以A(O′)点为测站点,用方位角定向测定1点在假定坐标系下的坐标两个测回取平均值,得到点
2)以1 点为测站点,以A点为后视点,直接测定2 点在假定坐标系下的坐标两个测回取平均值,得到点
3)以2 点为测站点,以1 点为后视点,直接测定B点在假定坐标系下的坐标两个测回取平均值,得到点
4)计算旋转方位角α旋转。
此处旋转方位角仍然是指原有测量坐标系指北方向顺时针转至假定坐标系指北方向的方位角。
经过外业施测得到假定坐标系下各点坐标后,由于A点、B点既有原来测量坐标系下的已知坐标,又有假定坐标系下的假定坐标。因此可以通过坐标反算公式计算AB边的已知坐标方位角α已知和假定坐标方位角α假定,从而计算旋转方位角:
需要注意的是,若α旋转>360°,则需自动减去360°;若α旋转<0°,则需自动加上360°。
(5)利用坐标转换公式直接转换坐标[5]。
在设计和施工部门,为了工作上的方便,常采用一种独立坐标系统,称为施工坐标系或建筑坐标系。施工坐标系的原点通常用O′表示,纵轴通常用A表示,横轴用B表示,如图4 所示,O′点在测量坐标系XOY下的坐标为(a,b)。
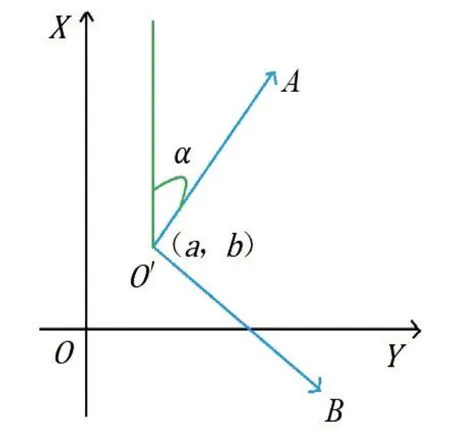
图4 施工坐标系统和测量坐标系
施工坐标系与测量坐标系往往不一致,因此,施工测量前常常需要进行施工坐标系与测量坐标系的坐标换算。施工坐标系AO′B转换到测量坐标系XOY的基本公式如式(9)所示:
参考施工坐标系与测量坐标系的坐标换算公式,可以得到如图3 所示的将假定坐标系下1 点、2点、B点坐标直接转换成测量坐标系下坐标的公式,比如1 点转换公式如式(10)所示:
若经过以上坐标转换后,若XB转与XB已知仍然不一致,YB转与YB已知仍然不一致,则还可以进一步参照一般方法进行缩放处理。
2 实例验证
2.1 试验场地概况
为了验证本文所探讨简化方法的可行性,以某省建筑行业技能竞赛实操为例。试验场地如图5所示:某施工现场原有个别控制点由于室外施工及场地硬化、绿化,遭到破坏,现留存的两个控制点A点、B点(CGCS 2000 坐标系统基准,中央子午线选择6 度带)互不通视,拟通过全站仪一级导线联测两个新布设的控制点1 点、2 点,得到CGCS 2000 坐标系统下的1 点、2 点坐标,从而为施工现场后续施工测量提供CGCS 2000 坐标系统基准。

图5 试验场地示意图
由于已知的A点、B点不通视,无法直接获取AB边的坐标方位角,只能绕过障碍物,依次布设1点和2 点,形成无定向附合导线A-1-2-B。
2.2 实测及计算分析
2.2.1 常规方法
1)已知数据如表1 所示。
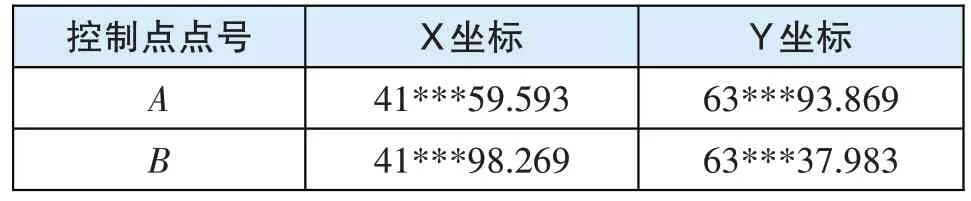
表1 常规方法已知数据单位:m
2)实测数据如表2 所示。
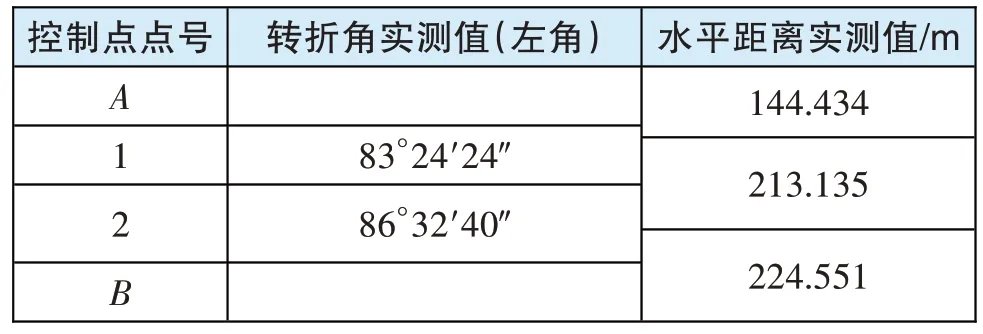
表2 常规方法实测数据单位:m
3)经过旋转、平移后计算结果如表3 所示。
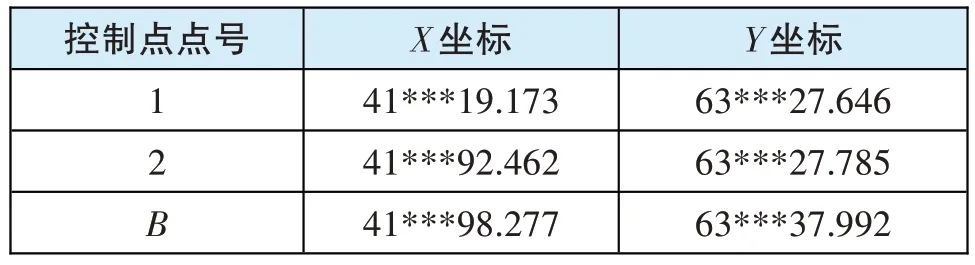
表3 常规方法旋转、平移计算结果 单位:m
4)经过旋转、平移、缩放后计算结果如表4 所示。
2.2.2 简化方法
1)已知数据如表1 所示。
2)简化方法实测数据如表5 所示。
3)计算结果如表6 所示。
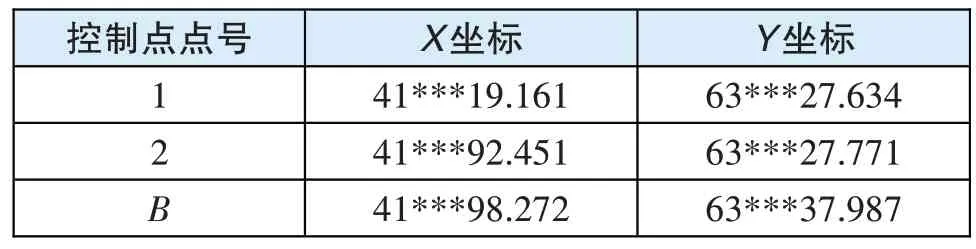
表6 简化方法计算结果单位:m
2.2.3 两种方法测量精度分析
为了比较两种方法测量的精度水平,对点A、点1、点2、点B应用GNSS 静态观测方法对4 个点位进行了同步观测,点A、点B作为已知点(CGCS 2000坐标系统基准,中央子午线选择6 度带),经约束平差后得到点1、点2 的精确坐标值分别为(41***19.163 m,63***27.635 m)、(41***92.453 m,63***27.774 m)。将该值作为点位精度检核的真值,分别与常规方法和简化方法比较,计算结果如表7,从表中可以看出两种方法的计算精度相当,最大不超过0.004 m。工程测量标准规定:对于建筑物施工控制网,控制网轴线定位误差不应大于20 mm,以上两种方法的计算精度完全满足实际工作要求。
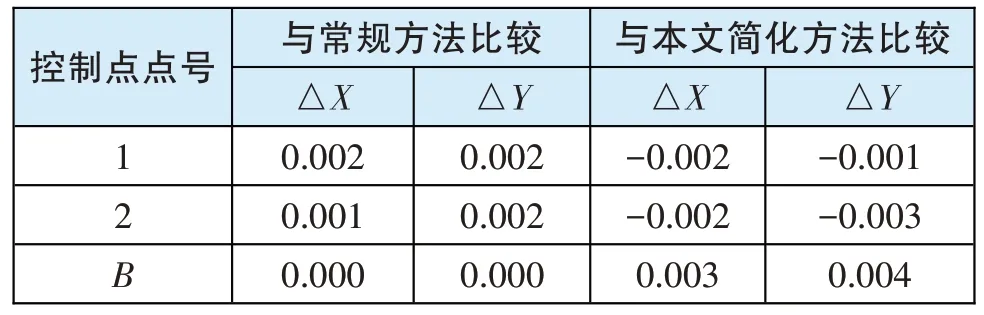
表7 精度检核计算结果单位:m
2.2.4 两种方法实施时间对比
经操作较熟练的测量员团队外业施测和内业数据处理,采用两种方法的实际用时如表8 所示。
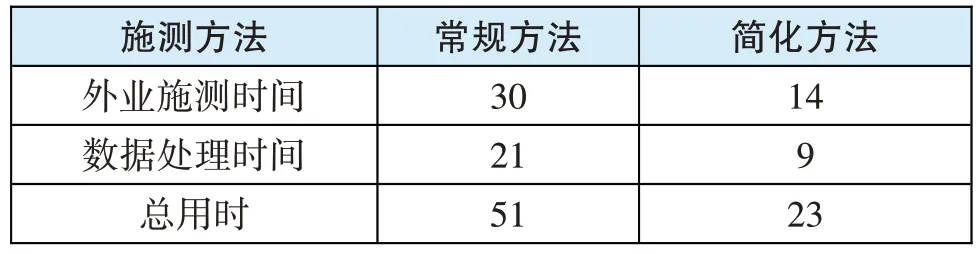
表8 两种方法实施时间单位:min
由表8 可知:简化方法的工作效率要比常规方法节约一半以上实施时间。
3 结语
本文结合实例对无定向附合导线点的常规方法和简化方法进行探析,得出以下结论:
1)采用无定向附合导线是一种可靠、实用、合理的控制方法,它简便、灵活、高效,在实际测量工作中具有可操作性和广泛的适用性。
2)通过验证,两种方法的计算精度相当,最大不超过0.004 m,完全满足实际工作要求。
3)从工作效率看,简化方法工作量更少,可以节约大约一半时间以上,简化方法可以在必须利用全站仪进行无定向附合导线测量的工作中推广使用。
