珠江河口磨刀门枯水期盐度统计模型

王 彪，朱建荣，吕爱琴

(1.上海市环境科学研究院，上海 200233； 2.上海水环境模拟与水生态修复工程技术研究中心，上海 200233；3.长三角区域生态环境联合研究中心，上海 200233； 4.华东师范大学河口海岸学国家重点实验室，上海 200062； 5.广东省水文局佛山分局，广东 佛山 528000)

珠江是我国第二大河，磨刀门为珠江河口八大入海口门之一，是主要的径流和泥沙出口，也是珠海和澳门主要水源地。20世纪90年代以来，珠江三角洲地区咸潮活动越来越频繁，持续时间增加，上溯影响范围越来越大，强度趋于严重，发展态势不容乐观[1]，严重影响了珠海和澳门的供水安全。

盐水入侵是河口地区普遍存在的一种径流、潮汐和风力等动力因子综合作用形成的一种自然现象。以往对珠江河口盐水入侵的大量研究表明，潮汐和径流是影响珠江河口盐水入侵的主要因子[2-6]。杨干然[2]根据海、河两大动力体系的强弱程度将磨刀门划分为径流型河口，认为盐度分布在洪季呈弱混合型，而枯季为缓混合型。李素琼等[3]则指出磨刀门无论枯、汛期咸淡水高度分层，盐水楔活动明显。乐灿等[4]基于珠江河口2016 年枯季同步观测盐度资料，总结了枯季八大口门同步盐度垂向分布和盐淡水混合特征，指出一般潮汐动力越强，盐度垂向分布的拐点位置越高。徐俊峰等[7]对珠江三角洲网河区一维水沙、含氯度输移数学模型和河口区二维水沙、含氯度输移数学模型进行联解，建立了珠江三角洲及河口区整体数学模型。为了更深入研究珠江河口的水流运动和盐度输移的三维特征，不少学者基于动力学过程的三维数学模型开展了大量研究[8-13]。Wong等[8]基于POM(Princeton ocean model)分析了珠江河口盐度梯度形成的羽状锋面的动力机制以及与冬季枯水期羽状锋面相关的小尺度环流。林若兰等[11]采用MIKE3 构建珠江东四口门三维水动力数值模型，对枯水期各风向下珠江口的水动力进行模拟，分析北风、东北风和东风对河口涨落潮流速、盐度分布、潮通量的影响。吕紫君等[12]基于SCHISM (semi-implicit cross-scale hydroscience integrated system model)建立了磨刀门三维盐度数值模型，利用该模型并结合盐通量分解方法，研究了磨刀门水道盐淡水混合特征及各驱动力对盐度通量变化的贡献作用。此外，陈水森等[14]基于经验模型分析了磨刀门水道含氯度及咸潮入侵最大距离与上游径流、河口盐度的关系；路剑飞等[15]利用引入滞后因子的径向基函数神经网络模型，以珠江口磨刀门水道为例,研究建立了盐度多步预测模型；周凡涵等[16]基于小波-神经网络构建了珠江口门区磨刀门水道的盐水入侵预报模型，对磨刀门盐水入侵进行了预见期1～3 d 的预测应用。总体上采用统计学经验模型对珠江河口盐水入侵的研究相对较少，原因是统计学模型主要针对特定站点、特定指标(如日均盐度、入侵距离等)进行统计学意义上的反演和预测，而基于动力方程的数学模型则能深入反演和预测河口盐度的时空变化。但统计学经验模型对基础数据要求较少，易于快速实现，在实际管理应用中仍有较强实用性。本文针对潮汐和径流两个主要动力因子，采用最小二乘拟合方法研究构建枯水期磨刀门盐度统计模型。

1 研究数据和方法

珠江河口磨刀门地理位置如图1所示，影响磨刀门水道盐水入侵最主要的两个动力因子是潮汐和径流。本文基于该动力机制，应用平岗泵站2005年1月1日至3月31日(时段1)和2005年10月1日至2006年2月23日(时段2)两个时段的盐度和潮位资料，以及同期的磨刀门上游西江的高要水文站和北江的石角水文站的合计径流量，建立盐度与潮汐和径流的统计关系模型。

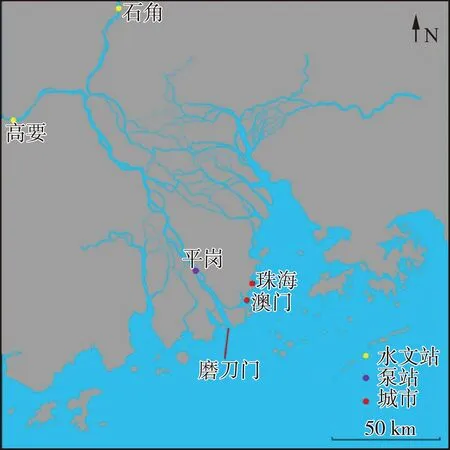
图1 珠江河口磨刀门地理位置Fig.1 Location of Modaomen in Pearl River Estuary

基于统计学方法构建盐水入侵统计模型，主要针对盐度的特征值，如盐度日平均值、日最大值和日最小值，挖掘其与相关动力因子之间的量化响应关系。本文主要构建日平均盐度与潮汐、径流动力因子之间的量化响应关系，日平均盐度通过对平岗泵站日内逐时盐度进行算术平均得到。潮汐动力因子以潮差进行表征，珠江河口潮汐为不规则潮，大潮期间为不规则半日潮，小潮期间为不规则全日潮，本文取日内最大的潮差作为当日潮汐动力强度。由于径流对盐度的影响不仅与近期的径流量大小有关，其前期的径流量大小对河口盐度也存在累积影响，因而分析径流动力因子对盐度的影响时，应考虑其前期的径流量情况，考虑潮汐的半月周期，本文取前15 d的平均径流量作为径流动力因子强度。处理前后的盐度、潮汐、径流如图2所示，原始盐度、潮位数据时间分辨率为1 h，径流量数据时间分辨率为1 d。原始数据表明，平岗泵站盐度和水位除了有日内变化特征外，具有显著的半月变化特征；径流量与盐度之间总体上呈现径流量大、盐水入侵弱和径流量小、盐水入侵强的特征。

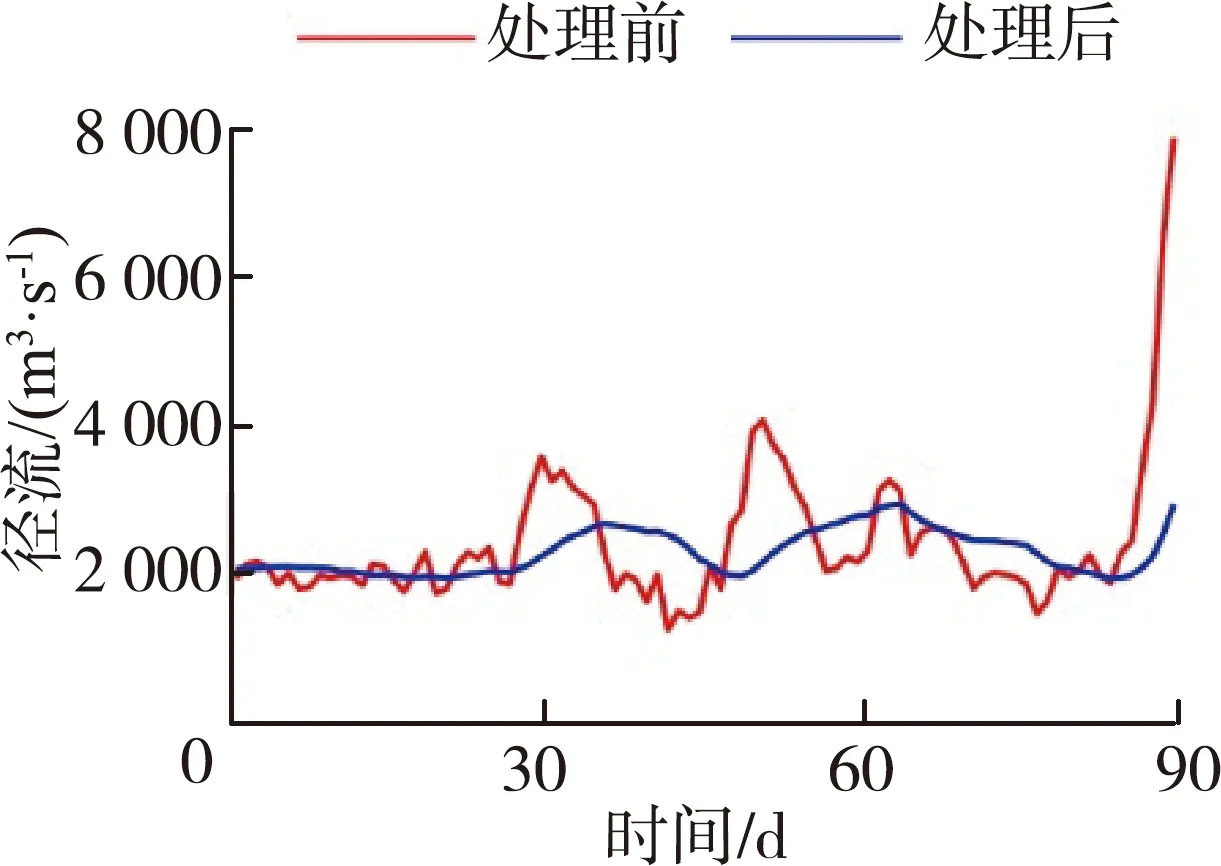
(a) 时段1流量

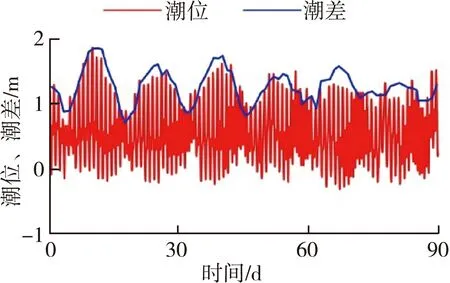
(b) 时段1潮位潮差

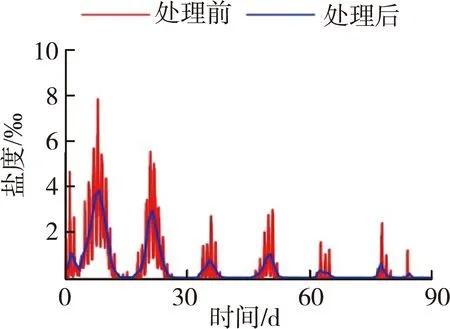
(c) 时段1盐度

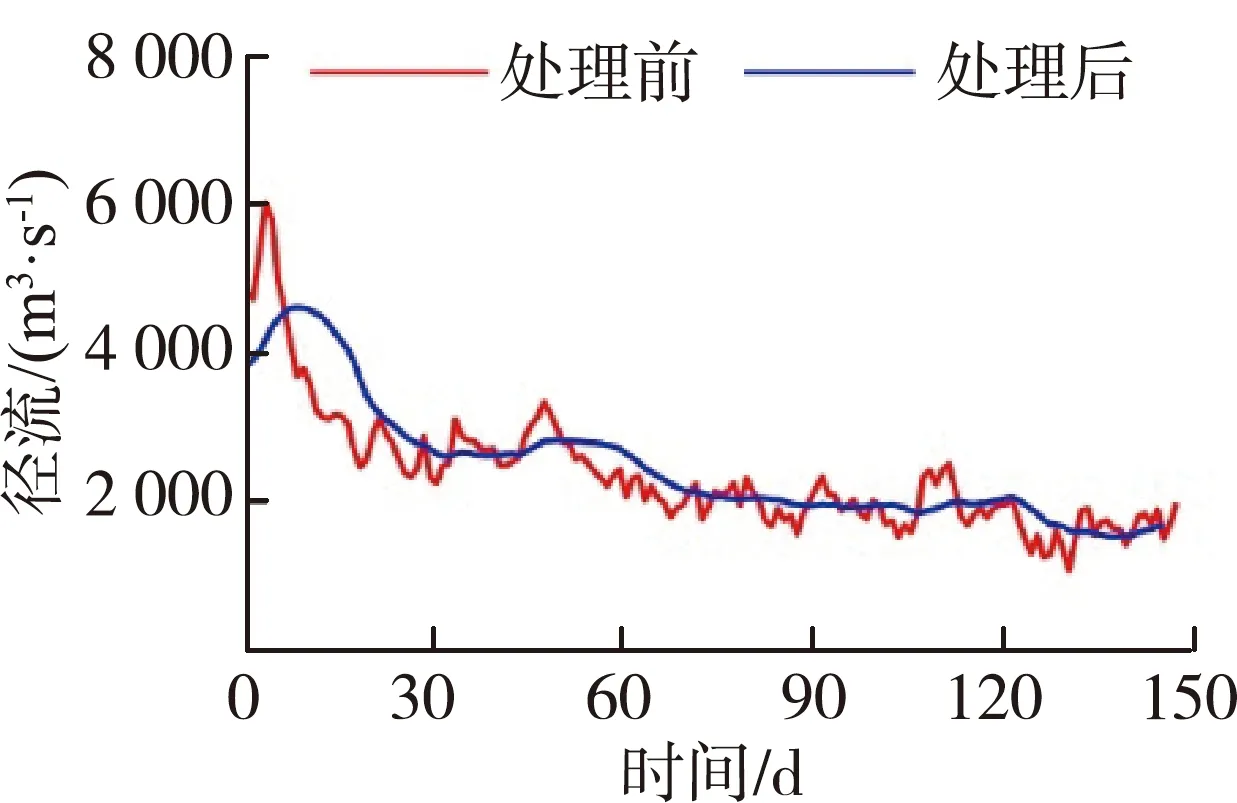
(d) 时段2流量

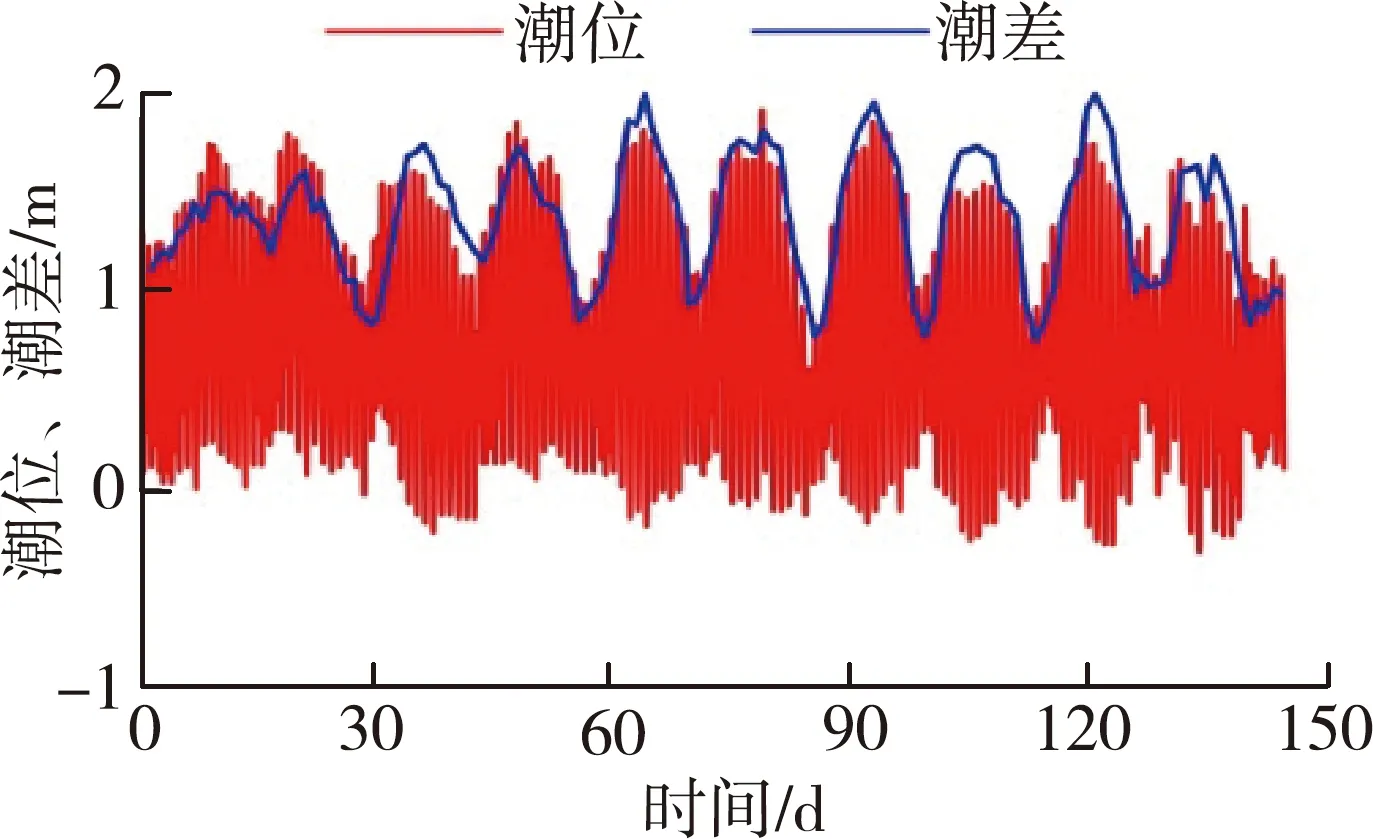
(e) 时段1潮位、潮差

(f) 时段2盐度图2 径流、潮汐和盐度随时间变化Fig.2 Temporal variations of runoff, tide, and salinity

由于外海高盐水入侵河口是一个复杂的动力过程，潮汐强度峰值与盐度峰值往往不会同步出现，而是存在一定的相位差。图2表明，日均盐度和潮差虽然都有明显的半月周期变化，但二者峰值确实存在明显的相位差。尹小玲等[17]参考珠江河口磨刀门宏观几何条件，建立了概化河口数值模型，分析指出由于混合过程时间效应，咸水运动调整过程呈现非线性特征，盐分向陆输运量在小潮后2～3 d达到最大。Wang等[18]通过珠江河口三维盐水入侵数值模型得出，该相位差动力成因主要是由于下游河口处洪湾水道汊道(图1中通向澳门的水道)的特殊地形与风和潮汐动力相互作用形成的。为使构建的盐度统计模型具有更好的适用性，需要对盐度和潮差进行相位校正处理。通过潮差和盐度的相关分析，发现将潮差进行3.5 d的相位校正处理后，二者相关系数达到最大。因此，下文统计建模中当日盐度对应的潮差为当日后第3和第4天的潮差均值。基于日平均盐度、第3和第4天的平均潮差和前15 d平均径流量数据(下文分别简称为盐度、潮差和径流)，本文采用统计学方法构建珠江河口磨刀门盐度统计模型。

2 模型构建

珠江河口盐水入侵主要受潮汐和径流的作用，且潮汐引起的半月时间尺度变化更为明显，故采用最小二乘法先拟合出盐度和潮差之间的关系式，据此预估出潮差对盐度影响；在此基础上，观测盐度去除潮差影响贡献，可得到一个盐度差，这个差值可认为是径流变化引起，通过拟合方法可找出盐度差与径流的关系式。将潮差-盐度拟合关系式叠加径流-盐度差拟合关系式，最终可得到一个综合关系式，此即本文构建盐度统计模型的基本思路。

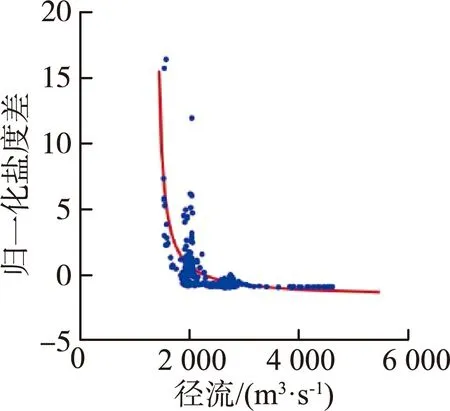
图3(a)给出了平岗泵站的盐度-潮差散点分布情况，可见二者为非线性关系，总体可认为是指数关系。因此采用指数关系对盐度和潮差进行拟合，通过最小二乘法得出拟合关系为

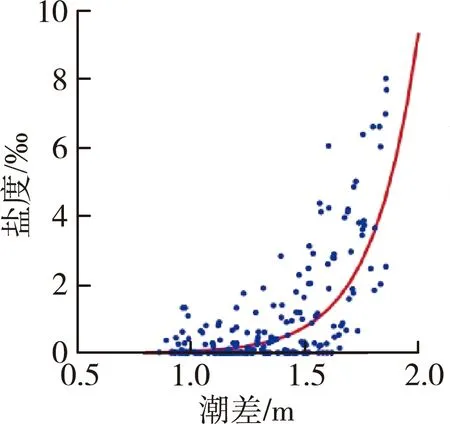
(a) 盐度与潮差

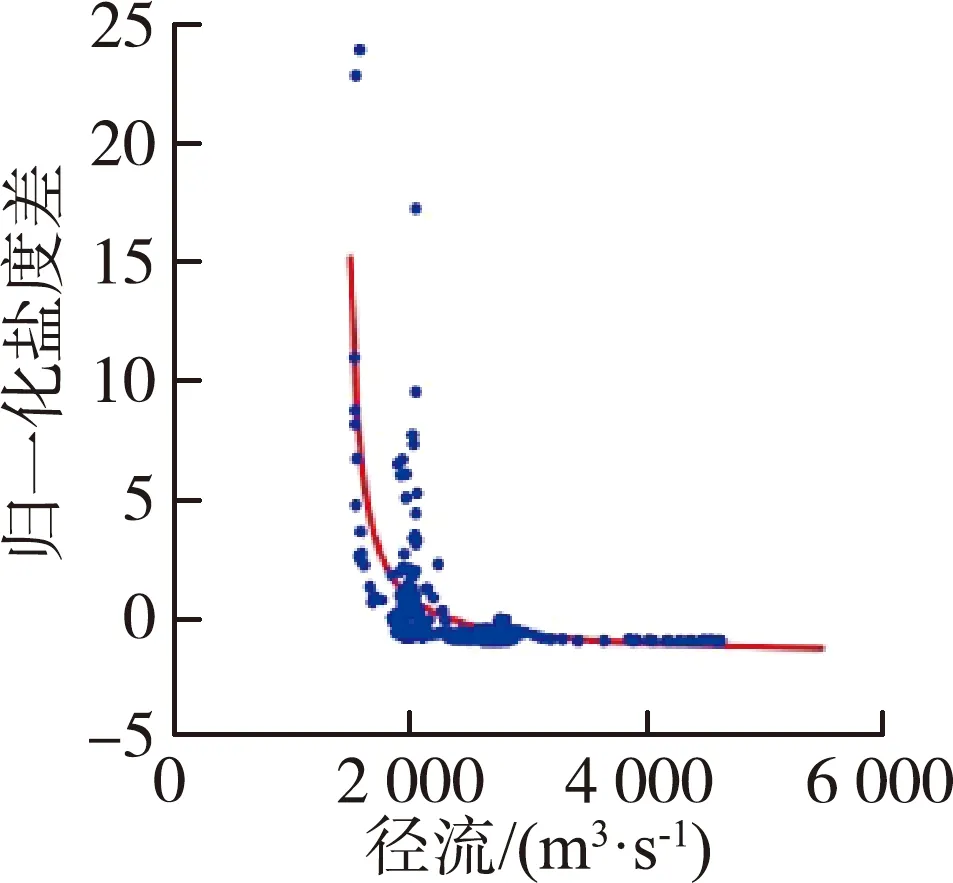
(b) 归一化盐度差与径流图3 盐度与潮差及归一化盐度差与径流的最小二乘拟合Fig.3 Least square fitting curves of salinity and tidal range as well as normalized salinity difference and runoff

SFT0=0.000 429 4e4.996HTR

(1)

式中：SFT0为盐度受到潮差影响的潮差拟合盐度；HTR为潮差。图3(a)中的曲线即为拟合曲线，潮差-盐度的拟合优度R2为0.90。基于此潮差-盐度拟合关系式，可计算出潮差随时间变化对应的潮差拟合盐度变化，其与实测盐度对比见图4。

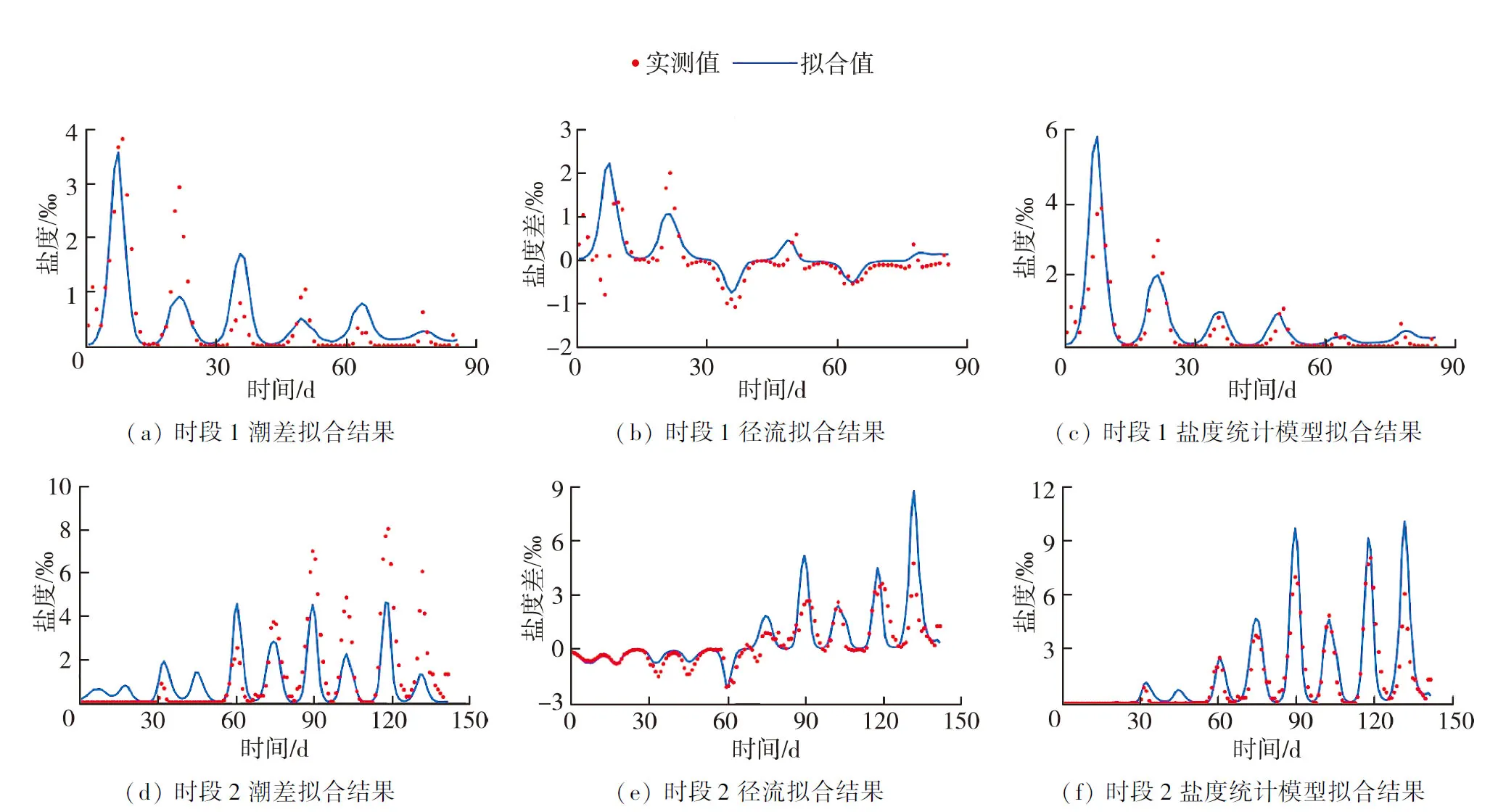
图4 实测盐度、盐度差与拟合结果对比Fig.4 Comparison of measured and fitting results of salinity and salinity difference

实测盐度中包含了潮差和径流的共同作用，在得到式(1)后，实测盐度减去潮差拟合盐度得到的盐度差可认为是径流的作用。若对此盐度差与径流直接进行拟合建模，会发现拟合效果不理想。分析其原因发现，此盐度差还受到潮形的影响，相同径流下大潮期间由于河口总体盐度大，对应的盐度差也相对较大；小潮期间对应的河口盐度总体较低，盐度差也相对较小。为了去除潮形不同引起的径流对应的盐度差差异，本文通过对盐度差进行潮形归一化处理，得到归一化盐度差：

SSD=SD/SFT0

(2)

其中

SD=S-SFT0

式中：SSD为归一化实测盐度差；SD为径流作用对应盐度差；S为盐度实测值。

通过分析归一化实测盐度差与径流之间的关系，发现二者具有反比例函数关系。因此，采用反比例函数进行归一化实测盐度差与径流拟合，得到径流-盐度差拟合函数：

(3)

式中：SQSD0为径流作用对应的归一化拟合盐度差；Q为径流。拟合曲线如图3(b)所示，径流-归一化实测盐度差的拟合优度R2为0.71。在此基础上，去归一化便可得到径流拟合盐度差：

SFQ0=SQSD0SFT0

(4)

实测径流作用对应盐度差SD与径流拟合盐度差SFQ0对比如图4所示。综合潮差-盐度拟合关系(式(1))和径流-盐度差之间关系(式(3)和(4))，可得到河口盐度统计模型表达式为

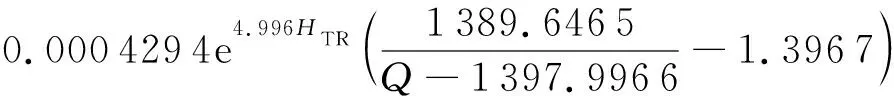
(5)

式中SiniF为盐度统计模型计算的盐度，其与实测盐度对比情况见图4。

3 修正盐度统计模型

盐度统计模型中进行潮差-盐度关系拟合时，实测盐度资料中包含了径流的贡献。通过式(3)和(4)可以计算出径流对盐度的贡献，将实测盐度S减去径流对盐度的贡献SFQ0，得到滤去径流影响的实测盐度SRFQ0，这个盐度与潮差关系更为紧密。基于SRFQ0重新与潮差进行拟合，能进一步提高模型精度。因此基于指数关系式用最小二乘法进行重新拟合，可得到潮差-盐度修正拟合关系式：

SFT1=0.001 127e4.372HTR

(6)

式中SFT1为修正潮差拟合盐度。

拟合曲线如图5(a)所示，两者拟合优度R2为0.92。滤去径流影响的实测盐度与修正潮差拟合盐度的时间序列对比见图6。由于时段2第130天附近径流拟合盐度偏高，因此滤去该径流影响的实测盐度出现负值，导致该时段拟合效果不好，但整体上修正潮差拟合盐度与实测盐度更为一致。

(a) 盐度与潮差

(b) 归一化盐度差与径流图5 盐度与潮差及归一化盐度差与径流的修正拟合Fig.5 Revised fitting curves of salinity and tidal range as well as normalized salinity difference and runoff

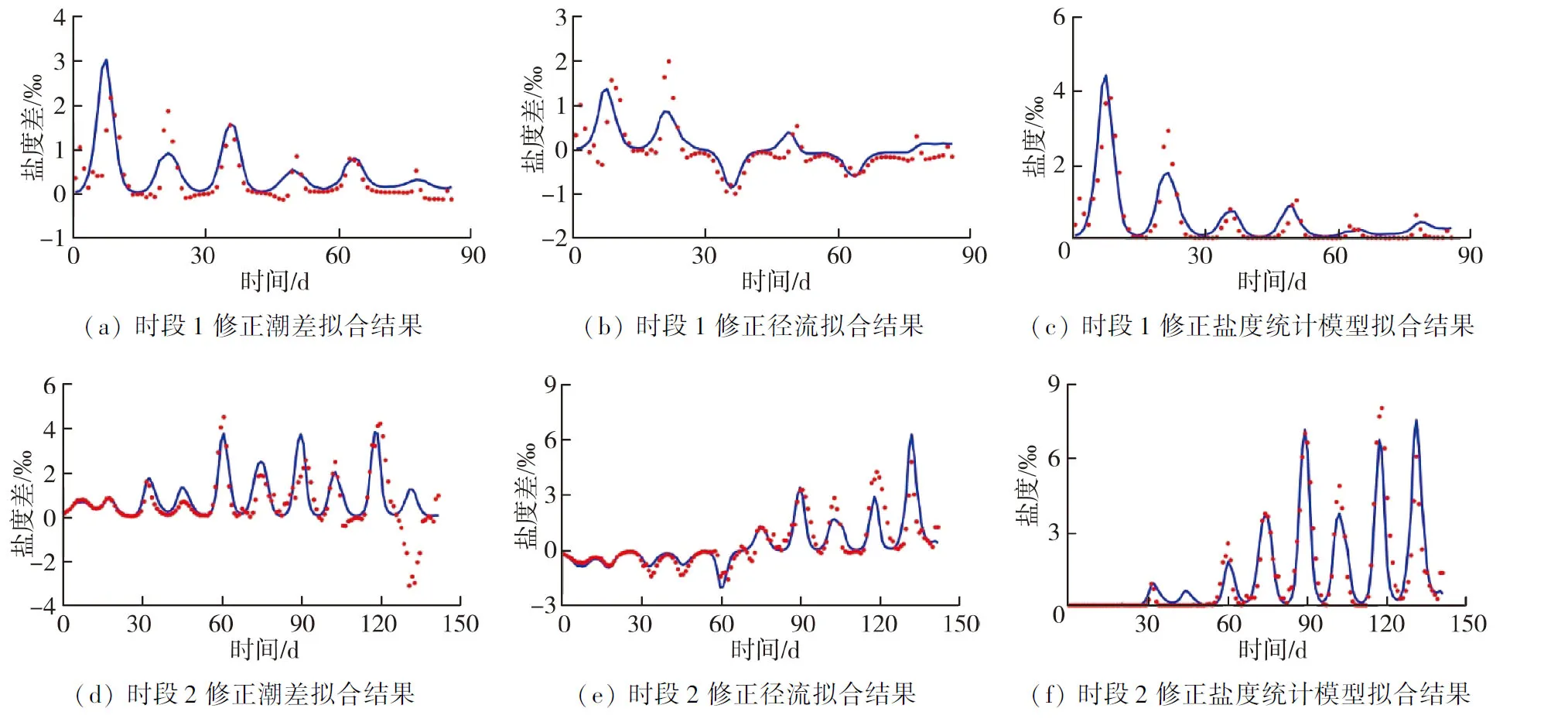
图6 实测盐度、盐度差与修正拟合结果对比Fig.6 Comparison of measured and revised fitting results of salinity and salinity difference

由于对潮差-盐度拟合关系进行了修正，相应的径流-盐度差拟合关系式也需要重新修正。采用与上文同样的方法，可得到修正归一化盐度差SQSD1与径流Q的拟合关系，进而去归一化便可得到修正径流拟合盐度差SFQ1：

(7)

SFQ1=SQSD1SFT1

(8)

修正归一化盐度差SQSD1与径流Q拟合曲线如图5(b)所示，两者的拟合优度R2为0.71。实测径流作用对应盐度差与修正的径流拟合盐度差的时间序列对比见图6。

通过潮差-盐度修正拟合关系(式(6))以及径流-盐度差的修正关系(式(7)和(8))，便可得到修正盐度统计模型：

(9)

式中SrevF为修正盐度统计模型计算的盐度，其与实测盐度对比情况见图6。

比较图6与图4，可以看出修正盐度统计模型比盐度统计模型更好地再现了盐度的实际变化。理论上，修正方法可以反复进行以提高模型精度，但实际应用中，第一次修正效果较为明显，此后修正效果的提高相对有限，建议采用一次修正为宜。

4 误差分析和讨论

本文实测盐度数据序列的均值为0.94‰。盐度统计模型计算的盐度序列均值为1.16‰，均值偏差为0.22‰，相对误差23.4%；修正模型计算的盐度序列均值为0.96‰，均值偏差约0.02‰，均值相对误差为2.1%。需要指出的是，虽然均值偏差、相对误差结果较好，但对于具体某天的盐度，尤其是实际盐度很低的情况，模型误差比较大。这主要是因为盐度很低，几乎为0时，河口不受盐水入侵影响，导致期间盐度与潮汐、径流量的相关性差，因而统计模型对此期间数据识别能力相应较差。即便统计模型计算出的盐度较小，由于实测盐度几乎为0，其相对误差也可能极大，没有代表性。实际管理应用中，往往关心盐水入侵较强导致的高盐度情况。

实际河口盐水入侵动力机制非常复杂，其影响因素除径流和潮汐外，还受河口地形变化、海平面上升以及风力等因素影响[19]。有研究指出，珠江磨刀门口门拦门沙的蚀退、口门向“河-波型”类型转化以及磨刀门水道受采砂形成河床下切均会加剧磨刀门水道盐水入侵[19]；不同风向对珠江河口盐水入侵影响不一，北风、东北风促进虎门盐水的入侵，东风则相反[11]。此外，短期特殊气象过程也会对河口盐水入侵过程造成影响，如台风“纳沙”期间，由于台风增水效应使得磨刀门盐度分布呈现出“双峰”特征。本文主要关注对河口影响较大的径流和潮汐两个动力因子，基于对径流和潮汐影响机理的认识和统计学方法提出了枯水期磨刀门盐水入侵统计模型构建方法。本文提出的盐水入侵统计模型与建模采用的数据样本紧密相关，若样本数据代表性不足则可能影响模型精度；考虑到河口地区水文地貌情况往往容易发生变化，进行模型预测应用时，还应注意建模数据的时效性。建议在数据积累较为丰富的区域应用本文提出的方法时，尽量采用代表性较好的近期数据进行建模，并采用不同批次的数据进行应用验证，以确保模型的可靠性。

5 结 语

基于日均盐度、日最大潮差、半月平均径流量等统计数据，分别采用指数函数和反比例函数进行最小二乘拟合得到潮差-盐度拟合关系式和径流-盐度差拟合关系式，并综合得到基于对潮差和径流拟合的珠江河口磨刀门盐度统计模型。针对盐度统计模型中潮差拟合的径流影响问题，通过滤去径流影响后对潮差拟合的方式进行了修正，得到修正盐度统计模型。构建的盐度统计模型和修正盐度统计模型能反映珠江河口磨刀门枯水期日特征盐度的变化过程。误差分析表明，盐度统计模型和修正盐度统计模型总体均值偏差分别约为0.22‰和0.02‰，相对误差分别为23.4%和2.1%，修正盐度统计模型比盐度统计模型具有更高的精度。河口地区盐度、径流和潮位资料较容易获取，基于本文提出的分离短时间尺度潮差影响和长时间尺度径流影响的盐度统计拟合方法，可快速建立河口盐度与潮差、径流的统计学模型，并预测河口盐水入侵程度，具有较好的实用性。