具有导流板直线翼垂直轴风力机气动特性分析

2023-02-04苏振鸾李岩佟国强冯放

排灌机械工程学报 2023年1期

苏振鸾，李岩,2*，佟国强，冯放

(1. 东北农业大学工程学院，黑龙江哈尔滨150030； 2. 东北农业大学寒地农业可再生资源利用技术与装备黑龙江省重点实验室，黑龙江哈尔滨150030； 3. 东北农业大学文理学院，黑龙江哈尔滨150030)

风力机根据其转轴与地面的相对位置，可将其分为垂直轴风力机和水平轴风力机[1].近年来，作为垂直轴风力机的经典类型——直线翼垂直轴风力机，凭借其结构简单、无需对风、噪声低以及适用于中小型离网式发电的优势受到了广泛关注[2].

目前，较低的启动性能和输出功率是直线翼垂直轴风力机面临的主要问题[3].为了解决这2个问题，国内外专家学者进行了大量研究.LI等[4]设计并研究了1种聚风装置，可以有效改善低风速条件下风力机的气动特性.王国付等[5]对仿生凹凸翼型的气动性能进行研究,发现凸前缘延缓了流动分离,而凹前缘提前了流动分离.RAHMAN等[6]对V型叶片进行研究,发现V型叶片的风力机在静态和动态研究中都表现出较高性能.LIU等[7]设计并研究了新型Gurney襟翼，结果表明与普通风力机相比，叶片带襟翼的风力机功率系数提升了20%以上.JIN等[8]研究了上游导流装置对直线翼垂直轴风力机性能的影响，发现导流装置可以减少负扭矩，同时可以显著提升风力机的气动性能.QASEMI等[9]研究了导流装置对风力机性能的影响，发现导流装置的安装使得风力机的效率提高了16.42%.这些研究都有效地改善风力机性能，但仍有不足，如装置成本过高、结构复杂，部分研究仅将辅助装置安装在同一个方向，这使得直线翼垂直轴风力机丧失了无需对风的优势.

为了改善风力机的气动性能，文中针对在直线翼垂直轴风力机周向布置的平板型导流板进行研究.利用二次正交旋转设计方法，以风力机的平均静态力矩为指标，对导流板的安装角度、宽度和导流板到风力机的距离进行研究，并得到效果最佳的导流板结构参数组合.通过风洞试验对安装和不安装导流板风力机的静态力矩特性、动态功率特性以及转速特性进行研究，并结合流场对试验结果进行分析.

1 风力机模型

采用额定功率为100 W的小型直线翼垂直轴风力机，风力机主要由4个采用NACA0018翼型的叶片组成，叶片弦长、高度分别为0.125和0.500 m，风力机旋转直径为0.6 m.为了保持风力机无需对风的优势以及导流板的效果，本研究采用的导流板个数是6个，导流板的安装角度θ、厚度I、宽度B以及导流板与风力机之间的距离l分别为-9°，0.003 m，0.18 m和0.092 m.安装导流板的风力机模型示意图如图1所示.另外，在图1a中对风力机的方位角α进行定义，选取逆时针方向为正方向.

图1 模型示意图Fig.1 Model diagram

2 研究方法

2.1 性能参数

风力机的性能参数包括尖速比λ、力矩系数CM以及功率系数CP.其中尖速比是风力机外径线速度与来流风速的比值，表示风力机的旋转状态，计算式为

(1)

式中：v为风力机外径线速度，m/s；U为来流风速，m/s；ω为风力机旋转角速度，rad/s；R为风力机半径，m.

力矩系数为风力机在气流中吸收能量与气流总能量的比值，计算式为

(2)

式中：M为风力机力矩，N·m；ρ为空气密度，kg/m3；A为风力机扫掠面积，m2.

功率系数为风力机在气流中吸收能量而产生的功率与气流总功率的比值，是评价风力机性能重要参数，计算式为

(3)

式中:P为风力机功率，W.

2.2 数值模拟

2.2.1 模型及设置

采用商业软件ANSYS Fluent进行数值模拟，由于文中使用的直线翼垂直轴风力机和导流板在展向具有一致性，因此采用二维数值模拟[10-11].为简化建模，在模拟过程中忽略了如转轴、横梁和法兰等连接部件.

数值模拟中的计算域示意图如图2所示.由图可知，计算域由矩形静止域和圆形旋转域组成，静止域的尺寸为10.0D×15.0D,旋转域的半径为1.1D(D为风力机旋转直径).静止域和旋转域通过interface边界结合，以保证数据的传输，静止域左侧设定为速度入口，入口速度为恒定的10 m/s.右侧为压力出口，出口压力设定与大气压相同.叶片和静止域上下边界设定为壁面.

图2 计算域及边界设定Fig.2 Computational domain and boundary setting

在数值模拟过程中，采用SSTk-ω湍流模型以及SIMPLE算法，动量、湍动量、比耗散率均采用二阶迎风格式，收敛误差设定为10-5.

2.2.2 网格无关性验证

网格对模拟结果有很大影响，过少的网格数量会使得到的结果准确性下降，而过多的网格数量将会带来更高的计算成本[12].为了准确且快速的得到计算结果，文中进行了网格无关性验证.以安装导流板的风力机在0°方位角时的静态力矩系数为指标，分别采用数量N为3.3万、10.7万、18.4万、30.7万、51.6万和99.9万的网格进行数值模拟，计算结果如图3所示.由图3可知，当网格数在10.0万～30.3万时，计算结果随着网格数的增加而增大.当网格数大于30.7万时，计算结果几乎不随网格数变化.为了兼顾计算的准确性以及计算成本，数值模拟部分网格采用30.7万，未安装导流板的风力机网格数为25.6万.

图3 网格无关性验证Fig.3 Grid independence verification

在网格划分过程中，全局网格最大尺寸小于叶片弦长，静止域与旋转域交界处采用相同的网格尺寸，以保证静止域与旋转域数据准确且稳定的传输.在叶片和导流板附近对网格进行加密设置，以捕捉叶片和导流板表面的流动分离.计算域网格如图4所示.

图4 计算域网格Fig.4 Grids in computational domain

2.2.3 数值模拟验证

为了验证数值模拟方法的准确性，通过数值模拟和风洞试验对风速为6 m/s时无导流板风力机模型的静态力矩系数进行对比，结果如图5所示.由图可知，2条曲线在趋势上基本一致，但数值模拟结果稍高于试验结果.这主要是因为在数值模拟过程中忽略了试验过程中存在的转轴和法兰等部件，且数值模拟过程中的环境过于理想.在二维数值模拟过程中并未考虑叶尖损失，这也是造成数值模拟结果高于试验结果的原因.

图5 计算方法验证Fig.5 Calculation method validation

2.3 风洞试验

采用开口射流低速风洞进行风洞试验，试验模型和风洞如图6所示.风洞长宽分别为9.1和2.3 m，风洞出口面积为1 m×1 m.风速可调为1～20 m/s.在试验过程中，风力机放置在距风洞出口1 m处，且风力机中心高度与风洞出口中心高度相同.通过风洞出口处的风速仪测量风速，静态与动态力矩均使用扭矩传感器测量，试验设备详细介绍见参考文献[12].

图6 风洞试验Fig.6 Wind tunnel test

3 导流板设计

3.1 因素水平选取

根据导流板及其与风力机位置尺寸关系，设定了3个参数的上下限，因素水平编码表见表1.安装不同结构参数的导流板时，风力机的平均静态力矩Mavg如表2所示.当导流板的宽度、安装角度以及距离分别为180 mm,-9°,92 mm时，风力机的平均静态力矩最大，达到1.415 N·m.当导流板的宽度、安装角度以及距离分别为120 mm,9°,68 mm时，风力机的平均静态力矩最小，为0.788 N·m.

表1 编码表Tab.1 Coding table

表2 数值模拟计算结果Tab.2 Numerical simulation results

3.2 方差分析

对计算结果进行方差分析，结果如表3所示.F值的大小代表着该因素的显著性，因素的F值越大则说明该因素显著性越高.P值则是衡量控制组和试验组之间差异大小的指标.由表可知，模型的F值较大，即表示模型差异具有统计学意义，而失拟误差不具有统计学意义，说明该模型是合适的.

表3 方差分析Tab.3 Analysis of variance

剔除不具有统计学意义项，得到平均静态力矩T和各因素的回归方程，计算式为

T=1.17+0.11x1+0.16x2-0.10x3+

(4)

综上，得到本研究条件下导流板最佳参数组合，即导流板的宽度、安装角度、距离分别为180 mm,-9°,92 mm.

3.3 交互项分析

在安装角为0°时，平均静态力矩随导流板宽度和距离的变化如图7所示.由图可知，当导流板到风力机的距离一定时，导流板宽度的增加，会使得风力机的平均静态力矩增大，但当导流板的宽度进一步增大时，风力机的平均静态力矩将下降.导流板到风力机距离对风力机平均静态力矩的影响也显示了类似的现象.

图7 响应面分析Fig.7 Response surface analysis

4 试验结果与分析

4.1 静态启动特性

在10 m/s风速下，对有无导流板的风力机进行风洞试验，静态力矩系数如图8所示.由图可知，导流板的安装有效地提升了风力机在各个方位角的力矩系数，其中0°,10°,30°和50°提升最为明显，分别提升了49.3%,59.9%,50.6%和150.0%.有无导流板风力机的最大力矩系数均在70°方位角时出现，与无导流板的风力机相比，有导流板风力机的最大力矩系数提升了15.2%.在1个旋转周期内，无导流板风力机的平均力矩系数为0.073，安装导流板后风力机的平均力矩系数增长到0.099，提升了35.6%.

图8 静态力矩系数Fig.8 Static torque coefficient

4.2 静态流场

为了进一步分析导流板对直线翼垂直轴风力机周围流场的影响，以70°方位角为例，对有无导流板风力机的压力和速度分布进行分析，如图9,10所示.

图9 压力和流线图Fig.9 Pressure cloud and streamline

由图9可知，在方位角70°时，安装导流板后，流场整体变化较大.导流型风力机上游叶片处的压差明显增大，且低压区由叶片前缘向叶片尾缘移动，从而增大叶片产生的扭矩，使得风力机的启动性能有了明显改善.

由图10可知，导流板的安装增大了流入风力机的气流速度，且在风力机迎风侧加速效果更加明显，与相同来流风速下无导流板风力机相比，有导流板风力机产生了更大的气动力，从而使其气动性能得到改善.

图10 速度云图Fig.10 Velocity cloud

4.3 功率特性

图11为10 m/s风速条件下，有无导流板风力机的功率系数随尖速比变化曲线.由图可知，有无导流板的风力机均在尖速比为1.0时达到最大功率系数，无导流板风力机最大功率系数为0.081，安装导流板后风力机的最大功率系数增长到0.113，提升了39.5%.

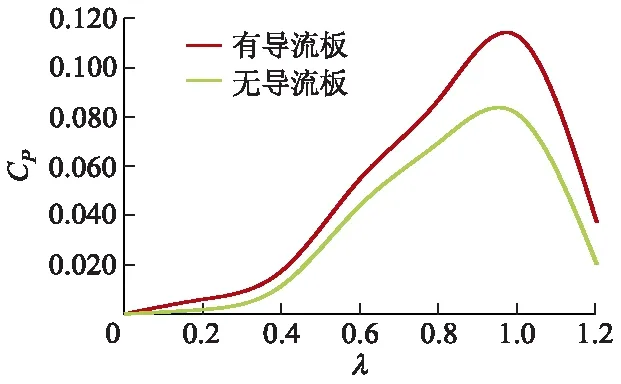
图11 有无导流板风力机功率系数Fig.11 Power coefficient of rotors with and without guide vane

4.4 转速特性

图12为风速在6和10 m/s时，有无导流板风力机的转速n随时间变化的曲线.

图12 有无导流板的转速Fig.12 Rotational revolutions of rotors with and without guide vane

由图12可知，导流板的安装使得风力机转速有了明显提升.当风速为6 m/s时，无导流板风力机约在330 s达到最高转速并稳定，最高转速为12.85 r/min.有导流板的风力机约在260 s达到最高转速并稳定，最高转速为17.05 r/min，与无导流板的风力机相比，有导流板风力机的转速提升了32.68%.当风速为10 m/s时，有导流板风力机的转速更快的达到稳定，约为200 s，而无导流板的风力机则需要约370 s才能使转速稳定.有导流板的风力机最高转速达到385 r/min，与无导流板风力机的351 r/min相比提升了9.68%.