江苏地区不同参考作物蒸发蒸腾量估算模型
2023-02-04王婷刘春伟张佩王让会邱让建周丽敏王蒙
王婷, 刘春伟, 张佩, 王让会,邱让建, 周丽敏, 王蒙
(1. 江苏省农业气象重点实验室/南京信息工程大学应用气象学院, 江苏 南京 210044; 2. 新疆维吾尔自治区气候中心,新疆 乌鲁木齐 830002; 3. 江苏省气候中心, 江苏 南京 210008)
1998年联合国粮农组织提出以FAO-56 Penman-Pontieth(PM)模型作为标准的参考作物蒸发蒸腾量ET0计算公式.但是PM公式所需气象参数多,在气象资料缺乏的情况下,对准确计算ET0有很大的难度,因此需要一系列简化的ET0计算公式估算参考作物蒸散量.
近年来,国内外有不少学者对不同区域的参考作物蒸散量的计算方法以及适用性进行了研究.BOURLETSIKAS等[1]和SHIRI[2]发现基于辐射的模型优于其他模型. VALLE JNIOR等[3]对基于动量传输、辐射、温度气象要素和综合法共21种ET0估算方法以及遗传算法(GA)计算的ET0进行比较研究,结果发现基于辐射的Priestly-Taylor方法更精确.刘晓英等[4]研究发现,基于温度的1985 Hargreaves在华北地区的适用性很好;研究表明Thornthwaite法在丹麦哥本哈根与实测值较符合;MC-Cloud法在国内研究较少. VALIPOUR[5]发现基于不同气候条件下的Valiantzas 1和Valiantzas 2模拟结果都较好. BOURLETSIKAS等[1]研究表明Copais法的结果比较好,但是这些方法在国内缺乏研究.
随着现代计算机学习技术的发展,一系列机器学习模型也被用于预测ET0.毛亚萍等[6]研究发现在新疆地区,SVM模型在日尺度和月尺度上可以代替PM法进行计算ET0.刘小华等[7]发现SVM模型能在江西省参考作物蒸散量的模拟中取得很好的精度.张皓杰等[8]研究发现ELM模型可以作为中国西北地区ET0计算的推荐模型.吴立峰等[9]利用蝙蝠算法优化ELM模型提高了ET0的计算精度.
XGBoost模型对数据波动较大、受外界影响较大、特征因子较多的数据集有很好的适用性,但是在国内ET0估算方面研究较少. FAN等[10]研究表明XGBoost模型在与SVM和ELM输入相同参数的情况下,XGBoost模型的计算结果更稳定、更精确,并且计算时间大大减少.
这些研究成果表明在不同的区域,ET0估算方法的适用性不尽相同,ET0的结果受到地理位置、温度、湿度、气压、风速、日照时数等的影响,影响因素复杂.然而,对于江苏省参考作物蒸散量计算方法的应用缺乏研究.文中旨在利用几种常用参考作物蒸散量的简化模型以及机器学习模型,计算江苏省的参考作物蒸散量,找到除了Penman-Monteith模型之外更简便的计算方法,以对实现江苏省水资源的合理配置、农业用水灌溉及科学管理具有一定的指导而做出贡献.
1 材料与方法
1.1 研究区域概况
江苏省位于中国东部沿海的中部及长江、淮河的下游地区,属于东亚季风区,又属亚热带和暖温带的过渡区.长江以南是苏南,长江以北、淮河以南是江淮,淮河以北是淮北.徐州位于淮北地区,属暖温带季风气候区;高邮位于江淮地区,属亚热带湿润气候区;昆山位于江苏南部,属北亚热带南部季风气候区.表1为站点信息,表中LAT为纬度,LON为经度,H为海拔,P为多年平均降雨量,Ta为平均空气温度,u2为风速.

表1 站点信息Tab.1 Site station information
1.2 数据来源
数据来自江苏省徐州、高邮、昆山3个气象站点的1957年1月至2019年12月逐日气象数据,包括最高气温Tmax、最低气温Tmin、平均气温Ta、气压p、相对湿度RH、风速u2、日照时数n、测站海拔高度H、测站经纬度等.
机器学习模型训练集为1957—2009年各站逐日数据,测试集为2010—2019年各站点逐日数据.经验模型采用的数据集也是2010—2019年各站点逐日气象数据.
1.3 XGBoost模型
XGBoost模型[11]是一种新颖的基于树增强的算法. 在时间步t可以给出表达式为
fi(t)=fi(t-1)+ft(xi),
(1)
式中:ft(xi)为时间步t的学习者;fi(t),fi(t-1)为时间步t和t-1的预测值;xi为输入数据.
XGBoost模型为了防止过度拟合采用的最终优化目标函数的解析表达式为
(2)

(3)
式中:γa为最小损失率;T为叶子节点数;λa为正则化系数;ω为叶子结点的得分值.
1.4 支持向量SVM
SVM[12]是一种二分类模型,公式为
(4)
式中:xj,yi为输入向量的纵坐标;k(xi,xj)为由输入向量xi转换而来的高维特征向量;αi为输入向量的权重;b为经验系数.
1.5 不同估算模型输入参数
表2为不同ET0估算方法的输入参数.XGB表示XGBoost模型;XGB,XGB1,XGB2,XGB3和SVM,SVM1,SVM2,SVM3分别代表2种模型不同输入参数下的预测结果;输入参数为Tmax,Tmin,RH,u2,n.公式中所包含的参数见所引参考文献.
1.6 数据评价方法
误差统计指标包括平均偏差MBE、均方根误差RMSE、绝对误差PE、一致性指数IOA和纳什效率系数NSE.其中MBE,PE和RMSE越接近于0,误差越小;IOA和NSE越接近1,误差越小.GPI为综合评价指数,GPI越大,模型精度越好.各统计变量计算公式为
(5)
(6)

(7)
(8)
(9)
(10)

2 估算结果及分析
2.1 月蒸散量变化
为了研究不同计算方法在月尺度上的差异,对徐州、高邮、昆山3个站点的月ET0进行分析;不同计算方法按表1所列的4种估算法划分:辐射法、温度法、综合法、机器学习模型.图1为月蒸散量的变化情况.
从图1可以看出,在徐州站,辐射法计算的ET0除模型JH外,其他方法与模型PM的月变化趋势一致.模型PM的最高值出现在6月,为5.18 mm/d,而最低值出现在1月,为1.68 mm/d; 模型PT的最高值为6.18 mm/d,最低值为1.63 mm/d,在1,2月和11,12月与模型PM基本重合,在其他月份偏大;模型Mak和Han的计算结果小于模型PM,模型Mak的最高值为3.80 mm/d,最低值为0.91 mm/d;模型Han的最高值为4.50 mm/d,最低值为1.18 mm/d;模型JH在1—4月和10—12月小于模型PM,在5—9月份大于模型PM,最高值出现在7月,为6.38 mm/d,而最低值出现在1月,为0.59 mm/d.温度法中,模型Har与PM的月变化趋势一致,最高值出现在6月,为12.61 mm/d,而最低值出现在1月,为2.72 mm/d,模型Har的明显偏高; 模型MC和Th与模型PM的趋势不一致,最高值出现在7月,分别为8.58和5.92 mm/d, 而最低值出现在1月,分别为0.39和0.14 mm/d; 模型MC在6—9月份明显高于模型PM,在其他月份明显低于模型PM; 模型Th在6月份与模型PM几乎重合,7和8月份偏高,其他月份明显偏低.综合法中,模型Co和V2与模型PM的变化趋势一致,最高值出现在6月,最低值出现在1月; 模型Co明显高于模型PM,最高值为7.62 mm/d,最低值为3.04 mm/d; 模型V2明显低于模型PM,最高值为3.27 mm/d,最低值为-0.04 mm/d; 模型V1与模型PM变化趋势不一致,最高值出现在7月,为6.01 mm/d,而最低值出现在1月,为1.50 mm/d,模型V1在4月份几乎与模型PM重合,而12,1,2和3月略小于模型PM,5—11月明显高于模型PM.
高邮站辐射法计算的ET0与模型PM的月变化趋势一致.模型PM最高值出现在7月,为4.66 mm/d,而最低值出现在1月,为1.67 m/d; 模型PT在1和2月、11和12月与模型PM基本重合,在其他月份偏大,最高值为5.86 mm/d,最低值为1.86 mm/d; 模型Mak和Han的计算结果小于模型PM,最高值分别为3.59和4.26 mm/d,最低值分别为1.05和1.34 mm/d; 模型JH在1—3月、11和12月小于模型PM,4月和10月几乎与模型PM重合,在5—9月份大于模型PM,最高值为6.39 mm/d,最低值为0.74 mm/d.温度法中,模型MC和Th与模型PM的月变化趋势一致,最高值出现在7月,最低值出现在1月; 模型Har明显偏高,最高值为11.19 mm/d出现在7月,最低值为2.69 mm/d出现在12月; 模型MC在6—9月份明显高于模型PM,在其他月份明显低于模型PM,最高值为9.03 mm/d,最低值为0.44 mm/d; 模型Th在6月份与模型PM几乎重合,7和8月份偏高,其他月份明显偏低,最高值为5.97 mm/d,最低值为0.22 mm/d.综合法与模型PM的变化趋势一致,最高值出现在6月,最低值出现在1月; 模型Co明显高于模型PM,最高值为7.12 mm/d,最低值为3.35 mm/d; 模型V2的明显低于模型PM,最高值为3.09 mm/d,最低值为0.02 mm/d; 模型V1在1—4月份和12月份几乎与模型PM重合,5—11月明显高于模型PM,最高值为6.02 mm/d,最低值为1.65 mm/d.
昆山站辐射法计算的ET0与模型PM的月变化趋势一致, 模型PM最高值出现在7月,为4.67 mm/d,而最低值出现在1月,为1.58 mm/d; 模型PT在1和2月、11和12月与模型PM基本重合,在其他月份偏大,最高值为5.83 mm/d,最低值为1.77 mm/d; 模型Mak和Han的计算结果小于模型PM,最高值分别为3.58和4.24 mm/d,最低值分别为0.99和1.28 mm/d; 模型JH在1—3月、11和12月小于模型PM,4和10月几乎与模型PM重合,在5—9月份大于模型PM,最高值为6.45 mm/d,最低值为0.79 mm/d.温度法中,模型MC和Th与模型PM的月变化趋势一致,最高值出现在7月,最低值出现在1月; 模型Har明显偏高,最高值为11.62 mm/d,出现在7月,而最低值为2.96 mm/d;出现在12月; 模型MC在6—9月份明显高于模型PM,在其他月份明显低于PM,最高值为9.81 mm/d,最低值为0.53 mm/d; 模型Th在5和10月份与模型PM几乎重合,6—8月份偏高,其他月份明显偏低,最高值为6.18 mm/d,最低值为0.33 mm/d.综合法与模型PM的变化趋势一致,最高值出现在7月,最低值出现在1月; 模型Co明显高于模型PM,最高值为7.07 mm/d,最低值为3.13 mm/d;V2明显低于PM,最高值为3.13 mm/d,最低值为0.05 mm/d; 模型V1在1—3月和12月几乎与模型PM重合,4—11月明显高于PM,最高值为6.08 mm/d,最低值为1.77 mm/d.
在3个站点,模型XGB和SVM均随着其输入参数变小,与模型PM模拟值的差距也越来越大.
2.2 相关分析
图2为徐州站不同ET0估算方法与模型PM日均ET0相关分析.
为了研究其他模型与模型PM在日尺度上的差异,利用相关分析,根据R2和斜率(k)判断各方法与模型PM的拟合程度和接近程度.R2越大,拟合程度越高;k值越接近1,表明该方法的计算结果越接近模型PM;k值小于1,表明该方法整体结果小于模型PM;k值大于1,表明该方法整体结果大于模型PM.从图2可以看出,在徐州站,根据拟合程度排序从高到低依次为R2(SVM)=R2(XGB)(0.98)>R2(XGB2)=R2(SVM2)(0.97)>R2(PT)=R2(Han)=R2(Mak)(0.96)>R2(Co)(0.95)>R2(SVM1)(0.93)>R2(V2)=R2(XGB1)(0.92)>R2(JH)(0.89)>R2(V1)(0.82)>R2(Har)(0.75)>R2(XGB3)=R2(SVM3)(0.72)>R2(Th)(0.51)>R2(MC)(0.46);根据斜率从高到低依次为k(Har)(1.99)>k(JH)(1.44)>k(Co)(1.37)>k(MC)(1.27)>k(PT)(1.24)>k(SVM)=k(XGB)=k(SVM2)=k(XGB2)(0.98)>k(V1)(0.97)>k(Han)(0.92)>k(SVM1)=k(XGB1)=k(Th)(0.90)>k(V2)(0.85)>k(Mak)(0.79)>k(SVM3)(0.74)>k(XGB3)(0.72).

图2 徐州站不同ET0估算方法与模型PM日均ET0相关分析Fig.2 Correlation analysis of daily average ET0 between each method and PM at Xuzhou station
图3为高邮站不同ET0估算方法与模型PM日均ET0相关分析.

图3 高邮站不同ET0估算方法与模型PM日均ET0相关分析Fig.3 Correlation analysis of daily average ET0 between each method and PM at Gaoyou station
从图3可以看出,在高邮站,根据拟合程度排序从高到低依次为R2(PT)=R2(Han)=R2(Mak)(0.98)>R2(SVM)=R2(SVM2)=R2(XGB)=R2(XGB2)=R2(Co)(0.97)>R2(XGB1)=R2(SVM1)(0.95)>R2(V2)(0.94)>R2(JH)(0.91)>R2(V1)(0.83)>R2(XGB3)=R2(SVM3)(0.76)>R2(Har)(0.75)>R2(Th)(0.50)>R2(MC)(0.47);根据斜率从高到低依次为k(Har)(1.87)>k(JH)(1.45)>k(Co)(1.38)=k(MC)>k(PT)(1.25)>k(SVM)=k(XGB)=k(XGB2)=k(SVM2)=k(V1)(0.97)>k(Han)=k(SVM1)(0.91)>k(XGB1)(0.90)>k(Th)(0.89)>k(V2)(0.84)>k(SVM3)(0.81)>k(Mak)(0.79)>k(XGB3)(0.77).
图4为昆山站不同ET0估算方法与模型PM日均ET0相关分析.
从图4可见,在昆山站,根据拟合程度排序从高到低依次为R2(PT)=R2(Han)=R2(Mak)(0.98)>R2(SVM)=R2(XGB)=R2(XGB2)=R2(SVM2)=R2(Co)(0.97)>R2(XGB1)=R2(SVM1)(0.94)>R2(V2)(0.93)>R2(JH)(0.91)>R2(V1)(0.82)>R2(XGB3)(0.72)>R2(SVM3)=R2(Har)(0.71)>R2(Th)(0.47)=R2(MC);根据斜率从高到低依次为k(Har)(1.85)>k(MC)(1.51)>k(JH)(1.45)>k(Co)(1.39)>k(PT)(1.25)>k(SVM)(0.98)>k(XGB)=k(XGB2)=k(SVM2)>k(V1)(0.95)>k(Han)=k(XGB1)=k(SVM1)(0.91)>k(Th)(0.90)>k(SVM3)(0.84)>k(V2)(0.82)>k(XGB3)(0.80)>k(Mak)(0.79).

图4 昆山站不同ET0估算方法与模型PM日均ET0相关分析Fig.4 Correlation analysis of daily average ET0 between each method and PM at Kunshan station
2.3 日蒸散量评价
表3为不同地区不同日蒸散量估算方法评价.表中Rank表示GPI值的排序.在徐州站,由表2和3可以看出,当输入参数为Tmax,Tmin,u2,RH和n时,SVM和XGB的GPI分别为0.52和0.51,模拟精度最好;当输入参数同为Tmax,Tmin,RH,n时,机器学习方法的精度高于综合法,XGB2和SVM2的GPI为0.42,而综合法中GPI值最高的模型V1为-0.36;当输入参数同为Tmax,Tmin和n时,机器学习模型的精度高于辐射法,XGB1和SVM1的GPI为0.21和0.23,而辐射法中模拟精度最高的模型JH的GPI为0.15;当输入参数同为Tmax和Tmin时,机器学习模型精度优于温度法.
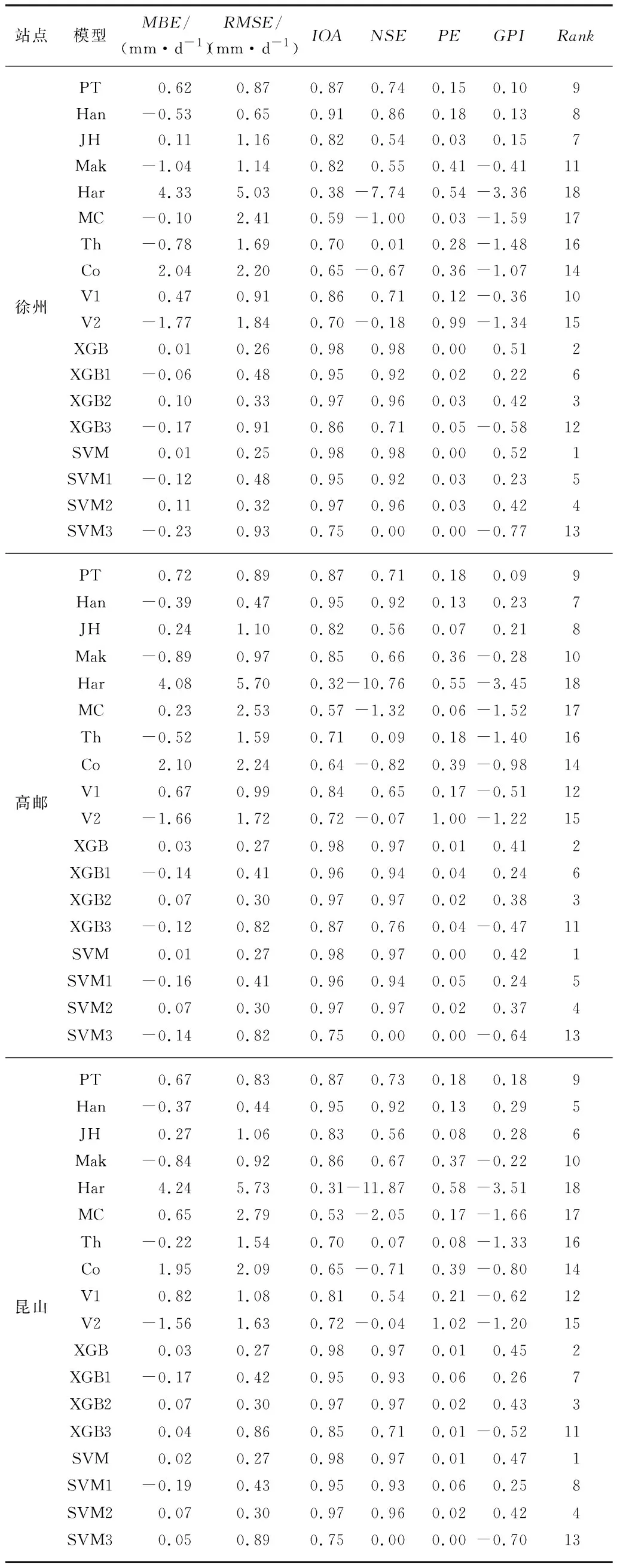
表3 不同地区不同日蒸散量估算方法评价Tab.3 Evaluation of daily average ET0 estimation methods in different regions
在高邮站,由表2和3可以看出,当输入参数为Tmax,Tmin,u2,RH和n时,SVM和XGB的GPI分别为0.42和0.41,模拟精度最好;当输入参数同为Tmax,Tmin,RH和n时,机器学习模型的精度高于综合法,SVM2和XGB2的GPI为0.37和0.38,而综合法中GPI值最高的模型V1为-0.51;当输入参数同为Tmax,Tmin和n时,机器学习模型的精度高于辐射法,XGB1和SVM1的GPI同为0.24,而辐射法中模拟精度最高的模型Han的GPI为0.23;当输入参数同为Tmax和Tmin时,机器学习模型模拟精度优于温度法.
在昆山站,由表2和3可以看出,当输入参数为Tmax,Tmin,u2,RH和n时,SVM和XGB的GPI分别为0.47和0.45,模拟精度最好;当输入参数同为Tmax,Tmin,RH和n时,机器学习方法的精度高于综合法,XGB2和SVM2的GPI为0.43和0.42,而综合法中GPI值最高的模型V1才为-0.62;当输入参数同为Tmax,Tmin和n时,辐射法中的模型Han和JH的模拟精度高于机器学习模型,其他的模拟精度低于机器学习模型;当输入参数同为Tmax和Tmin时,机器学习模型模拟精度优于温度法.
此外,根据表3可以看出,机器学习模型中GPI排序从高到低依次为GPI(XGB)>GPI(XGB2)>GPI(XGB1)>GPI(XGB3),GPI(SVM)>GPI(SVM2)>GPI(SVM1)>GPI(SVM3).机器学习模型随着其输入参数的减少,模拟精度依次降低.
3 讨 论
基于气象数据建立的基于辐射法、综合法、温度法等各种简化的ET0模型,虽然也能够较好地解决气象资料缺乏测量下的ET0计算问题,但是从图1可以看出,机器学习模型模拟值更接近模型PM;从表3可以看出,大多数经验模型的模拟精度不高.并且研究[23-24]表明,经验模型一般需要修正才能投入使用.机器学习模型模拟速度快,能处理复杂因子之间的非线性关系,对于ET0研究意义重大.
研究结果表明,在江苏省的这3个站点,在风速数据缺失条件下(只有Tmax,Tmin,RH,n),机器学习模型模拟精度优于经验模型;在只有Tmax,Tmin,n数据时,3个站点机器学习模型模拟精度优于常用的模型Mak和PT.在只有Tmax,Tmin数据时,机器学习模型模拟精度高于经验模型,这些结果都与已有研究结果[25]一致.但是,在只有Tmax,Tmin和n数据时,昆山站辐射法中模型JH和Han的模拟精度高于机器学习模型,在以往的文献中没有提到机器学习模型跟这2种模型对比,结果有待商讨.
文中将相同参数输入条件下的经验模型与2种机器模型对比,并没有考虑不同参数组合下的多种机器学习模型模拟精度.在以后的研究中,应该继续探讨不同参数组合下的更多的机器学习模型模拟精度.
4 结 论
1) 徐州站各方法月ET0中模型MC和Th的变化趋势与模型PM不一致,最高值出现在7月,最低值出现在1月;其他模型都与PM一致,最高值出现6月,最低值出现在1月.高邮站和昆山站各方法月ET0的变化趋势一致,最高值出现在7月,最低值出现1月.在月尺度上,3个站点中,机器学习模型预测值随着输入参数变少,与模型PM的差距越来越大.
2) 从决定系数可以看出,辐射法的拟合程度较好,R2大于0.85;温度法中模型Har的拟合程度较好,R2大于0.70,而模型MC和Th的拟合程度差,R2在0.50左右;综合法的拟合程度较好,R2大于0.80;机器学习方法拟合程度随输入参数变少,拟合程度依次降低,各方法在3个站点的差异不大.
3) 日尺度上,在相同输入参数情况下,徐州站和高邮站的机器学习模型模拟精度优于经验模型;昆山站辐射法中的模型Han和JH模拟精度优于相同输入参数下的机器学习模型,其他相同输入参数下的经验模型模拟精度低于机器学习模型.
