数控机床关键几何误差元素溯源研究*

李晓晓，孙付春，吴昊荣

(成都大学a.机械工程学院；b.电子信息与电气工程学院，成都 610106)

0 引言

数控机床在现代工业中起着不可取代的作用，多轴数控机床因其加工复杂曲面的高度柔性被广泛应用于机械制造行业[1]。目前，基于机床几何误差建模与辨识为基础，再进行机床几何误差补偿是提高机床精度的有效途径。几何误差产生于机床的设计、制造和装配阶段，属于先天性的静态误差，决定了机床的加工精度[2]。机床几何误差元素溯源作为机床几何误差建模与辨识的基础，近年来已经得到了广泛关注，学者们利用全局灵敏度分析法和局部灵敏度分析法开展机床几何误差元素溯源研究[3-4]。局部灵敏度分析法以机床静态常量的误差建模为基础，以几何误差元素作为分析变量，以空间误差模型作为敏感度计算模型，分别对空间误差模型中的X、Y、Z方向误差分量作偏微分运算，得到灵敏度系数，进而溯源机床关键几何误差源[5]。LASEMI等[6]利用直接矩阵微分法对数控机床的空间误差模型进行局部灵敏度分析，依据灵敏度系数将几何误差源划分为重要与非重要误差源。WANG等[7]根据局部灵敏度系数去除了非关键和线性相关的几何误差元素，简化了基于球杆仪测量的几何误差元素辨识过程；武剑等[8]在局部灵敏度分析的基础上，结合误差贡献度判定准则实现了机床关键几何误差元素溯源，为机床关键部件精度控制提供了新思路。全局灵敏度分析法的分析变量是机床几何误差元素，敏感度模型是空间误差模型，采用统计方法确定几何误差在空间中的分布，利用几何误差元素对误差模型的影响程度，从而来溯源机床关键几何误差源[9]。但全局灵敏度分析法的局限性在于：①机床误差源的分布特征无法准确获得；②概率分布要求大批量样本，对于具体某台机床误差情况则不准确[10-11]。

目前，绝大部分学者只利用局部灵敏度分析法或全局灵敏度分析法对机床空间误差元素溯源展开研究[3,5-7,12]，但是针对同一机床同时采用两种灵敏度分析法将会获得何种结果缺少研究；同时，两种灵敏度分析法同时溯源出的几何误差元素能为精确找出机床关键几何误差元素提供理论支持。基于此，针对局部灵敏度分析法和全局灵敏度分析法，以某卧式加工中心为例，分别溯源机床关键几何误差元素，验证两种方法的适用性，准确溯源出机床的关键几何误差元素。

1 利用旋量理论建立3轴数控机床空间模型

3轴数控机床包含了21项几何误差元素(GEs)，其中18项位置相关几何误差元素(PDGEs)和3项位置无关几何误差元素(PIGEs)[3]。如表1所示，δ、ε分别表示线性误差和转角误差。

表1 3轴数控机床几何误差元素

1.1 基于螺旋理论的多轴数控机床空间误差建模方法

机床运动链划分为刀具运动链和工件运动链，常被用于研究机床空间误差[13]。机床坐标系下，将刀尖点的实际运动位置相对工件被切削点的实际运动位置的矢量差定义为机床空间误差。利用螺旋理论分析运动链拓扑结构，推导各运动链运动学正解，构建基于全局坐标系下的空间误差模型[14]。

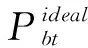
图1 机床工件运动连和刀具运动链

(1)

(2)

结合式(1)、式(2)，得理想状态下的刀具坐标系相对于工件坐标系的齐次变化矩阵：

(3)

实际运动过程中，因PDGEs和PIGEs的综合影响，切削点和刀尖点相对基坐标系原点将会发生偏移，对于单个运动轴而言，在运动过程中会产生6项PDGEs，将产生的运动误差同样用运动螺旋表示，那么理想运动螺旋到实际运动螺旋的变化便可看作是误差运动的结果[15]。与齐次变换理论类似，将6项PDGEs对应的误差运动矩阵相乘即可得到第i轴的最终PDGEs变换矩阵[15]，同理可得PIGEs变换矩阵，如式(6)和式(7)所示。

(4)

(5)

(6)

(7)

式中，Sji为第i轴相对于第j轴的垂直度。

故实际状态下的刀具坐标系相对于工件坐标系的齐次变化矩阵可表示为：

(8)

机床空间误差包括位置误差和姿态误差[3]，设刀尖点相对于刀具坐标系的位置和方向向量分别为Rpt和Rot，将实际状态与理想状态基坐标系下刀尖点相对切削点的偏差定义为机床空间误差ΔV，有：

(9)

式中，Perror为机床空间位置误差；Oerror为机床空间姿态误差。

1.2 卧式加工中心空间误差建模

图2为某型号的卧式加工中心结构及运动拓扑链，机床运动链包括工件运动链(床身-Z轴-工件)和刀具运动链(床身-X轴-Y轴-刀具)。在床身和工件上分别建立机床坐标系MCS和工件坐标系WCS。

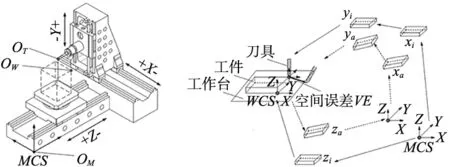
(a) 加工中心结构 (b) 运动拓扑链图2 卧式加工中心结构及运动拓扑链

根据基于螺旋理论的3轴数控机床空间误差建模过程，可推导出如图2所示卧式加工中心的空间误差模型：

(10)

式中，Perror为刀尖点在工件坐标系的实际位置向量(3轴机床中通常仅考虑位置向量)；Oerror为刀尖点在工件坐标系的实际姿态向量。

(11)

(12)

(13)

(14)

最终可得图2所示卧式加工中心的空间误差模型：

(15)

1.3 几何误差元素辨识

基于“十二线法”测量原理[16]，使用雷尼绍XL系列激光干涉仪，进行机床几何误差辨识测量实验，如图3所示。机床工作行程为800 mm×600 mm×600 mm，实验恒温环境温度为20±0.5 ℃。各运动轴的PDGEs辨识结果如图4～图6所示，PIGEs辨识结果如表2所示。

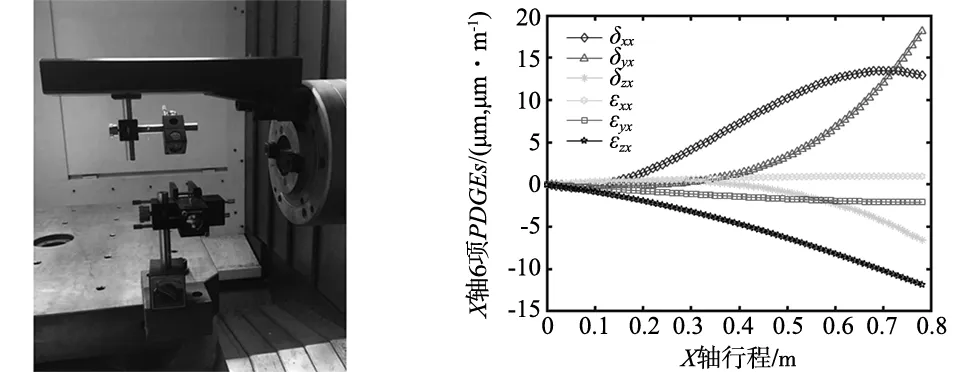
图3 机床几何误差辨识测量实验 图4 X轴PDGEs辨识结果

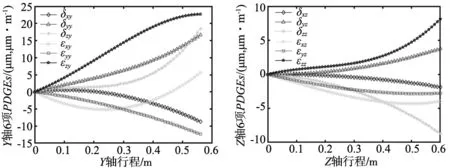
图5 Y轴PDGEs辨识结果 图6 Z轴PDGEs辨识结果

表2 PIGEs辨识结果 (μm·m-1)

2 局部灵敏度分析法溯源机床关键几何误差元素

由卧式加工中心空间误差模型可知，机床空间位置误差与几何误差元素和运动轴运动位置相关，可将其表示为[8]：

ΔP=f(G,M)

(16)

式中，ΔP=(ΔPxΔPyΔPz)为机床空间位置误差；G=(δxxδyxδzxεxxεyxεzxδxyδyyδzyεxyεyyεzyδxzδyzδzzεxzεyzεzzSxySyzSxz)为机床的21项几何误差元素；M=(x,y,z)为机床的运动位置。

由卧式加工中心空间误差模型可知，F是变量G和M的连续可导函数，将其按一级泰勒级数展开后，可得：

(17)

式中，S=∂f/∂M为机床空间位置误差对于21项几何误差元素的灵敏度系数矩阵，如式(18)所示。

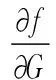
(18)

式(18)为卧式加工中心的误差灵敏度矩阵，反映出当运动轴运动位置和几何误差元素产生变化时，对X、Y、Z方向空间位置误差的影响程度。另外可从误差灵敏度矩阵中方便得到各几何误差元素的灵敏度系数Smi(m=x,y,z;i=1,2,3,…,21)。

2.1 关键几何误差元素辨识评定

误差灵敏度矩阵是溯源机床关键几何误差元素的基础。考虑到机床运动轴运动位置对各方向空间误差的灵敏度系数的影响，对Smi针对运动位置进行积分，实现灵敏度系数全局化，以统一量纲、便于对比分析。在实际加工中，机床空间误差直接影响机床加工精度，因此在溯源机床关键几何误差元素时，不仅需考虑运动轴运动位置，还需引入各几何误差元素的值。另外，统一机床关键几何误差元素的长度量与角度量，并将其无量纲化处理，会使溯源效果更佳。将各几何误差元素对机床实际加工精度的影响因子定义为误差贡献度，提出一则误差溯源评定准则，其具体可写作：

(19)

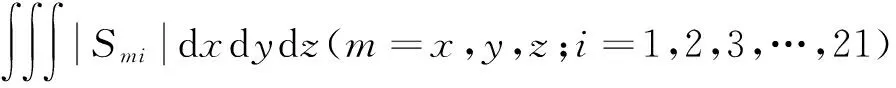
2.2 机床几何误差元素贡献度分析

在分析图2所示的卧式加工中心几何误差元素的误差贡献度时，需给出机床工作空间范围(600 mm×600 mm×480 mm)和几何误差元素的辨识结果，如表2所示。卧式加工中心的21项几何误差元素的数值，可参考机床工作运动极限位置处的几何误差值，即将X/Y/Z轴的工作运动极限值代入表2中的各几何误差元素辨识结果中，即可得到各运动轴几何误差元素的估值，计算结果如表3所示。

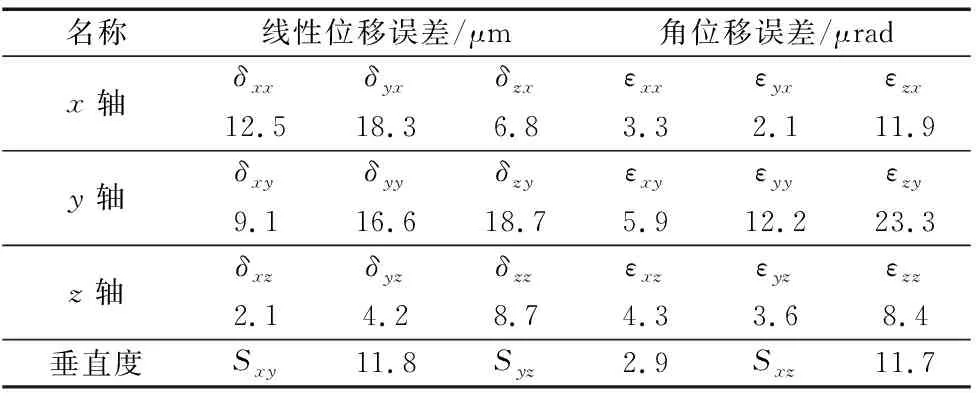
表3 机床运动轴几何误差元素评估值

将表3中的机床运动轴几何误差元素评估值与灵敏度系数代入式(19)，可计算出如图7所示的各部件误差在卧式加工中心空间位置误差上的贡献度。

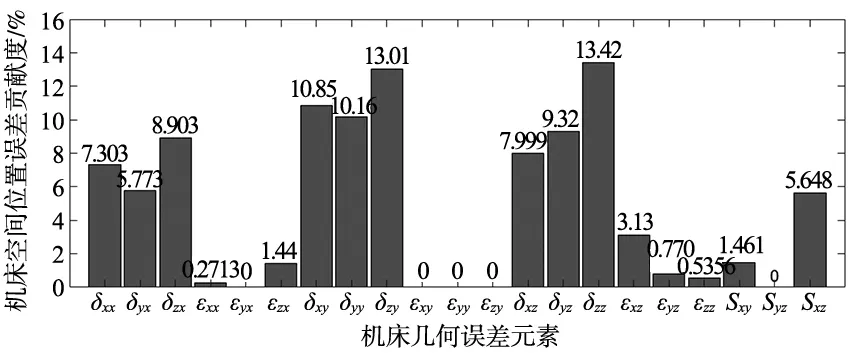
图7 卧式加工中心空间位置误差贡献度

图7的卧式加工中心空间位置误差贡献度分析结果显示：21项几何误差元素对机床空间位置误差的影响程度明显不同；δzz的误差贡献度值最大，达13.42%，δzy次之，为13.01%；δxx、δyx、δzx、δxy、δyy、δyz、δxz、δyz、Sxy这9项几何误差元素的误差贡献度值相对较高；且上述11项几何误差元素的误差贡献度值总和占全部21项几何误差元素误差贡献度的92.386%，说明表明这些几何误差元素是机床关键几何误差元素。

3 全局灵敏度分析法溯源机床关键几何误差元素

基于机床空间误差模型的全局灵敏度分析，本质是求解机床各项几何误差元素对机床精度的固有影响程度。综合考虑几何误差元素运动特性，借鉴正交试验设计思想在卧式加工中心的工作空间中选取25个试验点，设计多因素正交试验和单因素参数试验，对比试验结果，以快速、准确溯源机床关键几何误差元素。通过正交试验结果，分析试验因素对结果的影响程度[2]。在卧式加工中心21项几何误差元素的正交试验中，计算模型为机床位置误差模型，可表示为：

(20)

正交试验方差分析过程为：计算各因素对试验误差的离差平方和、自由度、平均离差平方和及F值；F检验。对于给定的显著性水平α，根据F分布表，查找α水平下的临界值Fα；通过比较Fj与Fα的大小，若Fj值大于Fα，则j因素对试验结果有显著影响，且偏差越大影响越显著，反之无显著影响。

借鉴正交试验思想，综合考虑几何误差元素与运动位置的关系以及试验点的空间均布性，以X、Y、Z轴运动坐标选择测点位置，选取5水平3因素，按照L25(56)正交表优选25个试验点，如表4所示。

表4 机床工作空间中试验位置选取 (mm)

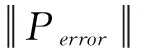
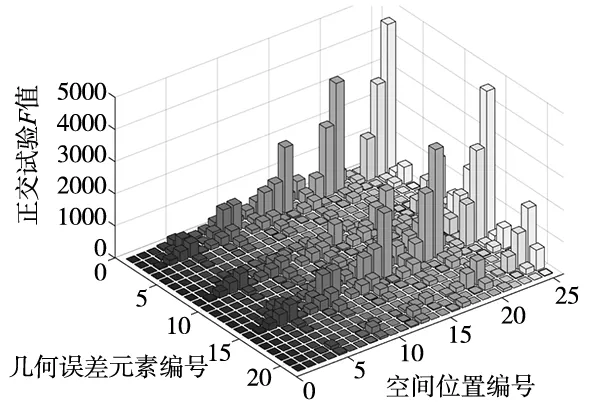
图8 位置误差正交试验F值

为溯源机床关键几何误差元素，选取α=0.01/0.05，查询F分布表得到等水平α下的临界值Fα=4.37/2.84。若F值大于Fα，则几何误差元素对试验结果有显著影响，且偏差越大影响越显著，反之无显著影响。综合位置误差和姿态误差正交试验结果，得到各试验点符合显著性检验的几何误差元素。

图8的位置误差正交试验结果显示：不同试验点的几何误差元素对位置误差的影响程度明显不同。试验点1为机床原点，F值均很小，为全局最小F值点；试验点25接近工作空间的极限位置，δyx、δyz的F值达到4 603.02和4 777.31，为全局最大F值点；试验点13位于工作台中心与Z轴极限的交点位置，δyx、δyz的F值为1 078.81、1 092.04，虽小于全局最大F值，但大于其他几何误差元素的F值。根据F分布表得到等水平α下的临界值Fα=4.37/2.84，可以看出：机床不同工作位置处的关键几何误差元素溯源结果相同，符合显著性检验的几何误差源所包含的几何误差元素项数也不同。因此需要计算各项几何误差元素在工作空间中各位置的F均值，以评估其对机床空间精度的影响程度，计算结果如图9所示。CHENG等[11]指出单个误差元素的灵敏度系数越高，对模型的影响越大，并且多个几何误差元素的灵敏度系数之和灵敏度系数之和的80%以上，表明这些几何误差元素是关键的几何误差元素。因此通过将25个位置点出的全部21项几何误差元素取均值后，发现：δxx、δyx、δzx、δyy、δzy、εzy、δxz、δyz、δzz、εxz、Sxy和Syz，这几项几何误差元素的正交试验F值总和超过全部几何误差元素F值总和的80%，故将其作为卧式加工中心的关键几何误差元素，在机床设计和安装调试时应予以重点关注。

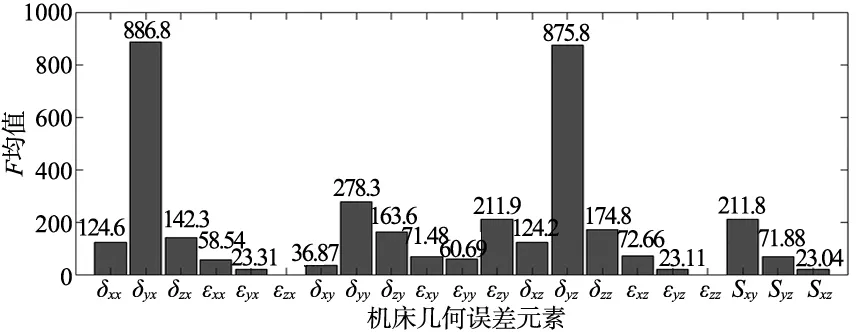
图9 位置误差正交试验F均值图

由此得出，卧式加工中心的关键几何误差元素为：δxx、δyx、δzx、δyy、δzy、εzy、δxz、δyz、δzz、εxz、Sxy和Syz，包含3项定位误差、5项直线度误差、2项转角误差和2项垂直度误差，共12项几何误差元素。

4 结论

通过对多轴数控机床关键几何误差元素溯源方法进行了深入研究，以某卧式加工中心机床为例，分别采用局部灵敏度分析法和全局灵敏度分析法溯源卧式加工中心关键几何误差元素。两种方法中的误差灵敏度系数的定义不同，机床的21项几何误差元素对卧式加工中心空间位置误差的影响程度也不同；采用局部灵敏度分析法溯源出机床11项关键几何误差元素，采用全局灵敏度分析法溯源出机床12项几何误差元素。尽管两种溯源方法得到的机床关键几何误差元素不同，但各运动轴的线性误差均为机床关键误差源，且对机床空间位置误差具有显著影响；另外，各运动轴的转角误差的灵敏度系数均较小，而垂直度误差的溯源结果并不相同，有待进一步的分析研究。