GA辅助NLS的GNSS-IR土壤湿度反演方法

王式太 姜新伟 殷 敏 王文贯 兰小艳 杨可心

1 桂林理工大学测绘地理信息学院，桂林市雁山街319号，541006 2 广西空间信息与测绘重点实验室，桂林市雁山街319号，541006 3 广西建设职业技术学院土木工程学院，南宁市罗文大道33号，530007

土壤湿度又称土壤含水率，是全球碳水循环中的重要环节，对于水文和气象研究、农业发展具有重要价值[1]。传统的土壤湿度测量方法(如中子仪法、烘干称重法、频域反射仪法、时域反射仪法等)操作过程较为复杂、探测范围小、时空分辨率较低[2]。而全球导航卫星系统反射(GNSS-R)技术可利用GNSS反射信号估计反射面相关参数[3]。Martin-Neira[4]通过GPS反射信号首次实现海洋高度测量；Larson等[5]根据海水潮汐变化率提出动态改正方法，可提高海洋高度变化情况下的测量精度。在土壤湿度方面，Larson等[6]认为土壤湿度与GNSS接收机记录的信噪比(SNR)震荡幅度有关，并表明该特征是由卫星直射信号与反射信号干涉形成。在此基础上，孙波等[7]考虑信噪比序列的相位、频率和振幅，通过GA-SVM构建该特征与土壤湿度的非线性回归模型；荆丽丽等[8]提出使用熵值法对2个频点的数据进行融合，从而提高土壤湿度的反演精度；文献[9-10]通过小波变换方法去除信噪比序列中的趋势项和高频误差，从而提高反演精度。

以上对于土壤湿度的反演研究均采用标准余弦函数拟合信噪比序列求解特征参数，未考虑信噪比振幅随时间和高度角的变化情况。因此，本文选择顾及阻尼因子的信噪比干涉模型，考虑信噪比振幅随时间和卫星仰角的变化，并通过遗传算法(GA)辅助非线性最小二乘方法(NLS)求解干涉模型中的反射信号参数，提高特征参数的求解精度。通过仿真实验分析该方法的有效性，并基于60 d的实验数据对2种不同计算方案进行对比分析。

1 GNSS-IR基本原理

信噪比(SNR)通常用于衡量信号的质量，定义为信号接收功率Pr与噪声功率N0之比，即

(1)

由于接收机实际接收到的为干涉信号，因此可将信噪比公式近似表达为：

(2)

式中，Ad为直射信号振幅；Am为反射信号振幅；ψ为直射信号与反射信号的相位差，由直射信号与反射信号传播路程存在差异(光程差)所致，可表示为：

(3)

式中，λ为卫星载波波长，θ为天线处卫星高度角[11]。将ψ代入式(2)，则SNR可表示为：

(4)

式中，φ为相对延迟相位。

接收机天线增益会随卫星高度角的增大而增大，接收的直射信号强度会随卫星高度角的增大而提高，而反射信号强度会随卫星高度角的增大而下降，导致整个信噪比序列呈现二次曲线变化趋势。通常使用低阶多项式拟合来表示该趋势，通过将原始信噪比序列减去趋势项来构建多路径信噪比SNRMP。低高度角范围下多路径信噪比可表示为余弦函数形式：

(5)

式中，AMP和φMP分别为多路径信噪比序列的振幅和延迟相位。若将sinθ视作变量，则：

(6)

由于sinθ非均匀变化，因此使用L-S谱(Lomb-Scargle periodogram, LSP)分析法求取频率f[12]。但AMP会随卫星高度角的增大而逐渐减小，仅使用余弦函数拟合会遗漏振幅衰减因素，进而影响特征参数的求解。振幅衰减主要与接收机天线增益和地面反射粗糙程度有关，因此Strandberg等[13]提出具有阻尼因子的多路径信噪比模型：

SNRMP=

(7)

式中，Λ为阻尼因子。

2 GA辅助NLS的原理与仿真

2.1 方案原理

遗传算法(GA)是基于模拟生物遗传进化的优化算法，主要包括编码、适应度函数、遗传算子(包括种群选择、交叉、变异)、运行参数4部分。相比于传统优化算法，GA具有2个特点：1)可全局最优解搜索，避免陷入局部最优解；2)适应度函数适用范围广，约束条件小。

信赖域算法的原理是首先确定一个信赖域半径，在该半径内计算目标函数的二阶近似极小值，该近似函数可表示为：

(8)

式中，q(k)(s)为目标函数f(x)的二次逼近式，s=x-xk；gk为目标函数在xk处的梯度；Bk为xk处Hesse阵。通过二次逼近式与目标函数的比值rk来确定下次迭代的信赖半径，rk可表示为：

(9)

rk越接近1说明二次逼近式越接近目标函数，则下一次迭代可考虑增大信赖域半径；当‖gk‖≤ε时，迭代停止。

在进行多路径信噪比延迟相位求解时，可以通过最小二乘法构建参数方程，其中待定参数分别为AMP、h、φMP、Λ。其参数方程可表示如下。

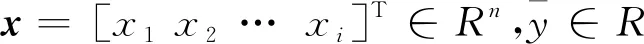
(10)

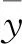
由于误差方程为非线性方程组，非线性最小二乘法在对误差平方和求其最小值对应的特征参数时，使用传统的信赖域算法容易因初值设置不当而陷入局部最优(极小值点而非最小值点)，从而影响求解结果，而仅使用GA时求解精度不高。因此本文提出采用GA辅助NLS求解最优参数，具体方案为：1)使用二阶多项式拟合信噪比趋势项，将原始信噪比减去趋势项计算SNRMP；2)将SNRMP和sinθ输入到具有阻尼因子的函数模型构建误差方程中；3)使用GA求解误差方程，计算初始参数AMP、h、φMP、Λ；4)将初始参数赋值给信赖域算法进行迭代，获得最终相位参数φMP。

2.2 实验仿真

由于多路径信噪比延迟相位无法获得真值，本文利用MATLAB人为设置参数来进行仿真实验，对比2种算法的求解能力。其中，AMP设置为2，h设置为190.5 cm，φMP设置为2.452 5，Λ设置为46，高度角设置为5°～20°，均匀生成100组数据，然后加入标准差为0.2的随机误差。设置2种方案：1)方案1，采用传统余弦函数模型，利用L-S谱分析方法求解SNRMP和sinθ存在的频率关系，赋值初始参数h，统计多路径信噪比最大值并赋值初始参数AMP，解算相位参数；2)方案2，采用顾及阻尼因子的信噪比干涉模型，通过GA辅助NLS进行求解。

由图1可见，方案2可以较好地拟合SNRMP曲线，而方案1在高度角过高或过低情况下均无法很好地拟合SNRMP曲线。表1(单位cm)为2种方案100次仿真实验的相位求解结果。

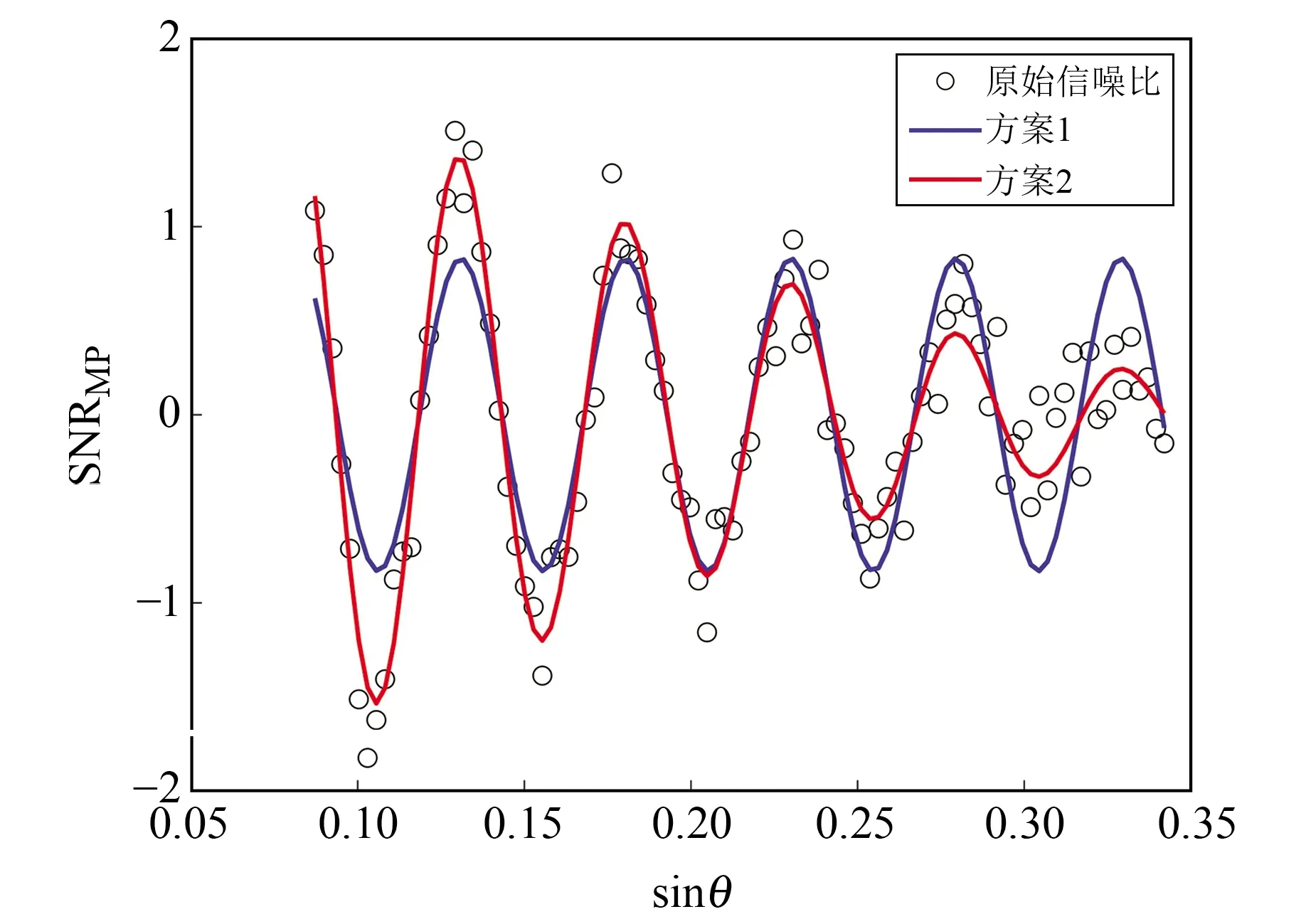
图1 2种方案仿真结果Fig.1 Simulation result of the two schemes

表1 方案1与方案2误差统计

由表1可见，方案2均方根误差、最大误差、最小误差均优于方案1，其中RMSE减小32.5%。

3 实验与分析

3.1 实验概况

本文实验数据来自PBO网站提供的P043测站2015年doy182～241观测数据(共60 d)，所使用的接收机型号为Trimble NERT9，同时使用钢制三脚架安置，天线罩为SCIT，天线型号为TRM59800.80。该测站用于土壤湿度分析的年份较早，具有一定代表性。测站地势平坦、地形无明显起伏，有利于进行土壤湿度实验。土壤湿度参考值来自https:∥cires1.colorado.edu/portal/index.php，采样间隔为1 d。

3.2 实验数据处理

通过RTKLIB软件解算各个卫星的高度角和方位角，并提取L1波段(λ=19.05cm)信噪比。选取观测时间较长且运动轨迹较好的卫星数据(高度角最高可达70°)，由于测站周边地形无明显差异，故对不同方位角数据不作要求。通过低阶多项式拟合去除SNR中的趋势项构建SNRMP，完成数据预处理。通常情况下，当卫星高度角设置为5°～30°时，土壤湿度反演效果较好[12]，但对P043测站各个卫星进行去趋势项处理后，卫星高度角在25°以上时基本无明显干涉特征。由于本文所选数据月份为7～9月，该期间植被生长茂盛，过低的高度角数据容易受到植被遮挡影响，最终选取5°～25°高度角范围进行实验。同时为探究不同高度角范围的反演结果，本文设置3个高度角取值范围(5°～15°、5°～20°、5°～25°)进行实验。

图2为采用2种方案对G28卫星2015年doy241的SNR数据进行拟合，从图中可以看出，在处理真实卫星观测文件时，方案2的拟合效果优于方案1。

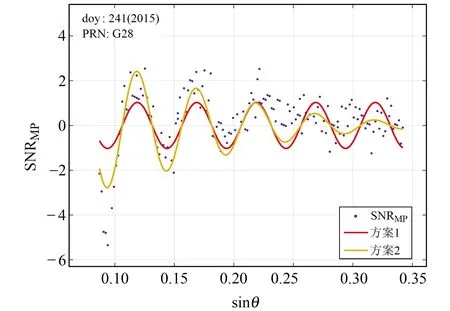
图2 2种方案拟合结果Fig.2 Fitting result of the two schemes

由于篇幅限制，3种不同高度角的计算结果中，仅给出G14卫星5°～15°、G23卫星5°～20°高度角范围内2种方案的建模结果(图3～4)。由图可见，G23卫星方案1和方案2精度基本相当，G14卫星方案2精度有较为明显的提升。在对G14卫星进行实验时，使用方案1余弦函数解算时出现部分异常相位(图3红圈)。

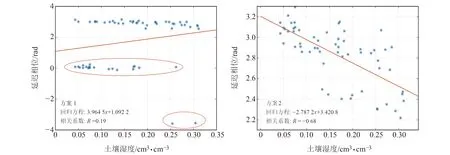
图3 5°～15°高度角范围下 G14卫星2种方案的回归模型Fig.3 Regression model of the two schemes of G14 satellite at 5° to 15° elevation angle

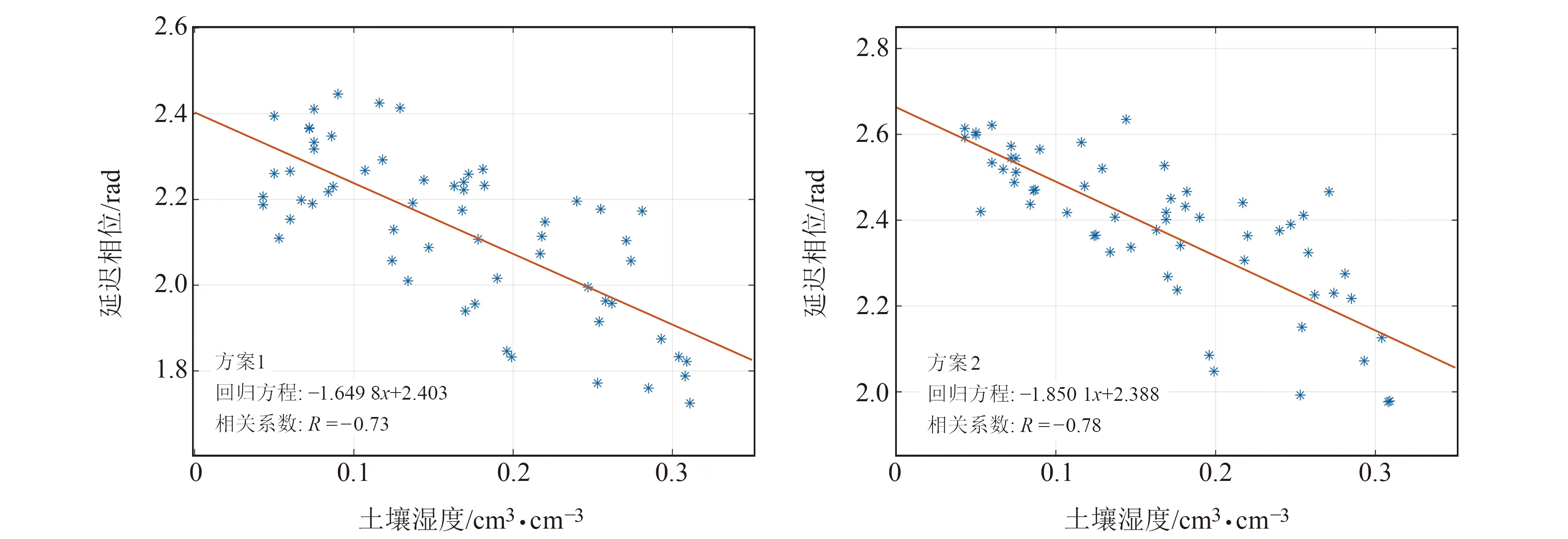
图4 5°～20° 高度角范围下G23卫星2种方案的回归模型Fig.4 Regression model of the two schemes of G23 satellite at 5° to 20° elevation angle

本文统计不同高度角范围下2种方案对G14、G22、G23、G28、G30五颗卫星的线性回归结果，包括相位和土壤湿度的相关系数R、决定系数R2、均方根误差RMSE、平均绝对误差MAE等，结果如表2～4所示。

由表2～4可见，5颗卫星在3种高度角范围内的15种情况中，5种情况下方案1和方案2精度相当，10种情况下方案2较方案1精度有显著提高，占比66.7%。由此可知，相较于方案1，方案2可有效提高反演精度，而方案1由于延迟相位求解会出现部分异常值而导致整体结果变差。对于G14、G22等信号状况较差的卫星，方案2在3种高度角范围内均能减小φMP的粗差值，显著提升反演精度。对于G23这种信号较好的卫星，2种方案在3种高度角范围内精度相当；对于G28和G30卫星，方案2相较于方案1有不同程度提高。相较于方案1，G28卫星方案2相关性提高1.22%～38.33%(由于G28在5°～15°高度角下存在异常值，故不统计该数据)，R2提高3.44%～94.10%，RMSE减小2.13%～30.3%，MAE减小5.13%～33.93%。相较于方案1，G30卫星方案2相关性提高3.75%～33.33%，R2提高5.72%～76.06%，RMSE减小6.12%～24.24%，MAE减小2.7%～28.3%。

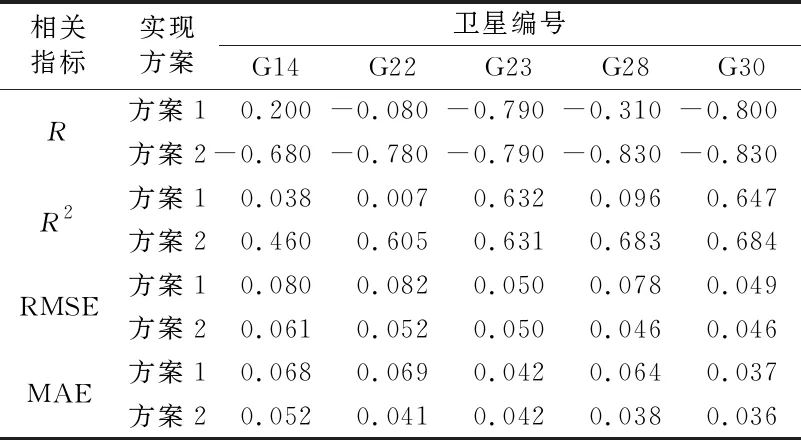
表2 5°～15°高度角下各方案相关系数及拟合精度统计

表3 5°～20° 高度角下各方案相关系数及拟合精度统计

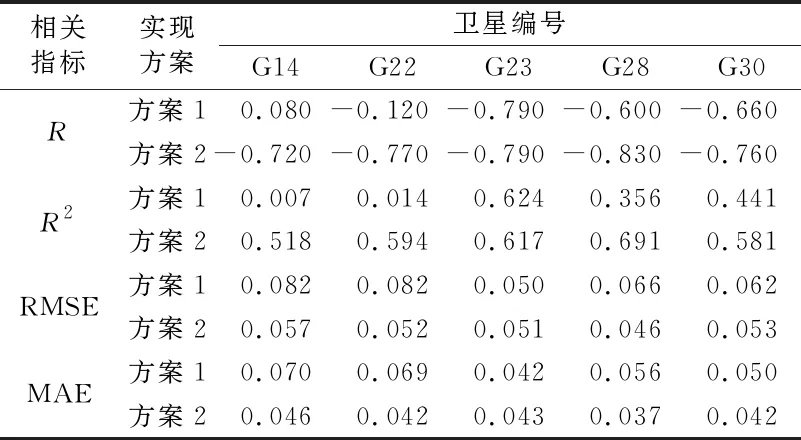
表4 5°～25° 高度角下各方案相关系数及拟合精度统计

图5 各卫星不同高度角的相关性Fig.5 Correlation of different elevation angles of each satellite

本文统计2种方案5颗卫星在不同高度角范围下求解相位和土壤湿度的相关系数(图5)，由图可见，相较于方案1，方案2受高度角的影响较小，结果更加稳定。表5为3个高度角范围内的平均相关系数以及最大差值，由表可见，相较于方案1，方案2在3种高度角范围内的整体相关系数更高，且整体反演结果更加稳定，受高度角范围变化的影响较小。

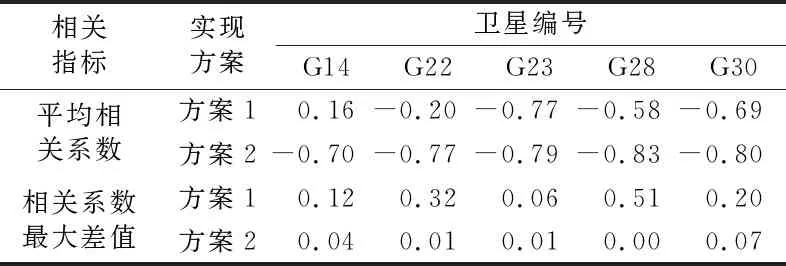
表5 各高度角范围的平均相关系数

3.3 多星线性回归测试

文献[14]表明，多星线性回归可以有效提高反演精度和改善单星反演的跳变现象。本文利用§3.2两种方案所求的延迟相位进行多星线性回归，以此验证输入数据的优劣。由于5°～15°高度角下G14、G22、G28卫星的方案1结果出现一定的延迟相位跳变，从而影响多元线性回归模型的精度，因此本文仅使用5°～20°和5°～25°高度角下G23-G28、G23-G30、G28-G30、G23-G28-G30四种卫星组合方式进行验证，结果见表6。

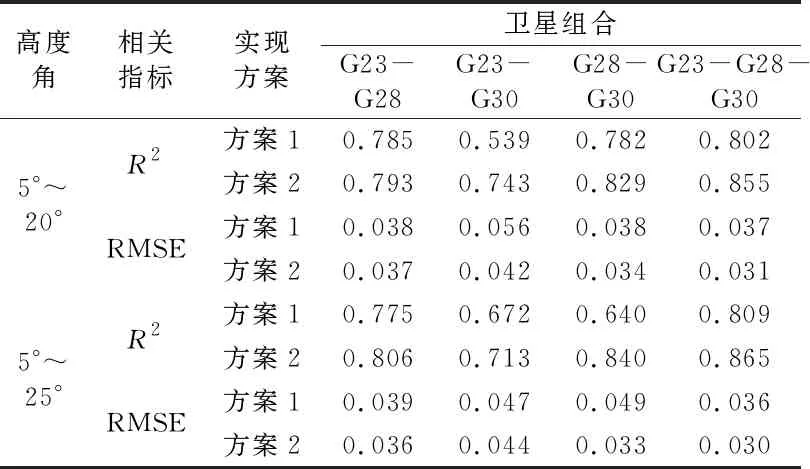
表6 多星组合线性回归测试

由表6可知，相较于单星线性回归，多星线性回归反演精度有较为明显的提高，同时不同方案输入的数据对多星线性回归也具有较为明显的影响。相较于方案1，5°～20°高度角范围内方案2延迟相位R2提高1.02%～37.85%，RMSE减小2.63%～25%；5°～25°高度角范围内方案2延迟相位R2提高4%～31.25%，RMSE减小6.38%～32.65%。

4 结 语

1)本文使用GA辅助NLS方法对顾及阻尼因子的多路径信噪比模型进行延迟相位求解，结果表明，除G23卫星精度与传统方法差别较小外，其他卫星均有不同程度的提升。忽略传统方法反演产生的部分异常数据后，GA辅助NLS方法比传统方法R2提高5.72%～76.06%，RMSE减小6.12%～24.24%，MAE减小2.7%～28.3%。

2)计算3个高度角范围内的相位数据可知，GA辅助NLS受高度角范围影响较小，高度角变化对相关性的影响不大，相关系数最大差值为0.07，余弦函数方法最大差值为0.51。

3)GA辅助NLS所求的延迟相位用于多星线性回归时精度也有较为明显的提升，相较于余弦函数方法，5°～20°高度角范围内RMSE平均减小13.60%，5°～25°范围内RMSE平均减小15.85%。