大规模GNSS网多进程并行解算研究

王建伟 程传录 赵 辉 冯在梅 刘晓云 田 婕 马润霞

1 自然资源部大地测量数据处理中心，西安市友谊东路334号，710054 2 自然资源部第一航测遥感院，西安市友谊东路334号，710054

大规模GNSS网作为实现高精度位置服务的重要基础设施，在国家和地区坐标参考框架建立与维持、实时定位、灾害防御、板块运动分析等多个领域得到广泛应用。参考站数量的不断增加使得大规模GNSS网运算量剧增，传统串行解算方式时效性较差，难以满足当前需要。由于GNSS数据处理技术难度高、专业性强、软件开发周期长，因此利用并行计算技术对已有的通用高精度GNSS软件进行并行化改造成为一种高效化、实用化的选择。

目前，国内学者在大规模GNSS网快速解算方面已取得一些研究成果[1-5]。在云计算方面，李林阳[6]针对未来云化和微服务等应用场景，采用云计算技术对大规模全球GNSS网数据进行高效处理。在多节点分布式计算方面，陈正生等[7]利用Bernese软件分布式处理引擎BPE及已有的并行计算函数库等，实现大规模GNSS网数据的快速处理；白帆等[8]分别利用Spark大数据集群和Hadoop平台技术，基于GAMIT软件实现大规模GNSS网子网级分布式处理。在单节点并行计算方面，崔阳等[9]基于共享内存多核系统优势，从数据并行和任务并行两方面实现大规模GNSS网抗差估计的并行化，从而提高解算的时效性。

相较于共享内存模型，分布式内存模型具有各节点数据传输高延迟、进程通信开销大等缺点，使得上述基于GAMIT软件的子网级粗粒度并行解算时效性的提升十分有限。目前，GAMIT软件官方尚未提供并行处理引擎，针对该软件的并行化研究进展相对迟缓。因此，本文基于GAMIT/GLOBK软件及共享内存模型，从时间和空间两个维度研究大规模GNSS网基线的并行解算方法。

1 概 述

1.1 并行

根据费林分类法，计算机体系结构共有4种类型，即单指令流单数据流(SISD)、单指令流多数据流(SIMD)、多指令流单数据流(MISD)和多指令流多数据流(MIMD)。上述4种类型分别对应串行、数据并行、任务并行、任务和数据并行(图1)。

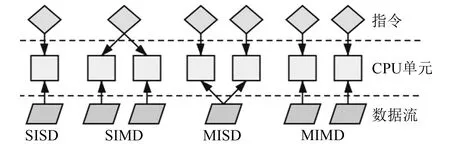
图1 费林分类法Fig.1 Flynn’s Taxonomy

并行计算是时间资源最大化的一种尝试，具体可通过多线程(multi-thread)或多进程(multi-process)方式来实现。利用进程池(process pool)技术来优化和管理进程活动，可实现进程的重用以减少创建进程的额外开销，从而提高并行系统的性能。

1.2 并行计算模型

并行计算模型是硬件和内存体系结构的一个抽象。根据阿姆达尔定律，针对一个并行计算问题，假设程序串行部分所占百分比为α，则n个处理器的加速比S(n)为：

(1)

从式(1)可以看出，加速比S(n)与处理器个数n呈正相关，即加速比会随处理器个数的增加而增大，但最大值不会超过1/α。由古斯塔夫森定律可知：

S(n)=n-α(n-1)

(2)

古斯塔夫森定律表明，对于一个并行计算问题，首先设置并行解决一个问题所允许的时间，再根据时间来确定问题的规模。

目前使用最广泛的并行计算模型主要包括共享内存、分布式内存/消息传递、大规模并行处理(massively parallel processing，MPP)、工作站集群等。不同于分布式内存，共享内存具有虚拟内存数量较多、所有处理器可以同等地访问该内存中的数据和指令、不存在消息交换、无需花费较长时间来进行消息传递等优点，因此该模型下的并行计算加速比及资源利用率最高。

2 大规模GNSS网并行解算设计

本文基于共享内存体系结构和GAMIT/GLOBK软件，首先利用进程池技术分别设计大规模GNSS网在时间(多时段)和空间(多子网)两个维度下的数据并行(SIMD)算法，然后将二者融合，设计时空一体化的双层并行解算策略。并行算法设计的核心是任务的等价分解与解算结果的有机组合，具体包括任务分解、任务分配、映射和组合4个步骤。

2.1 GAMIT/GLOBK数据处理

GAMIT由多个功能不同的模块组成，主要包括数据准备和数据处理2大部分。数据处理部分包括生成参考轨道(ARC)、计算残差和偏导数(MODEL)、周跳探测与修复(AUTCLN)、最小二乘平差(SOLVE)等模块。这些模块既可以独立运行，也可以通过批处理命令联合在一起运行，共同完成高精度GNSS数据处理和分析全过程。GAMIT软件一次只能解算一个时段的同步观测站数据，单时段基线解算流程如图2所示。GLOBK是一个卡尔曼滤波器，可以对GAMIT的基线结果进行网平差处理。GLOBK主要由globk、glred和glorg三种模块组成，分别用于时间域和空间域的数据合并、重复性分析、求解最佳坐标等操作，GLOBK平差流程如图3所示。GAMIT/GLOBK按照特定的项目目录结构进行数据处理。

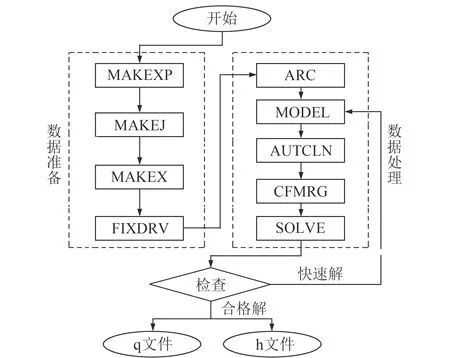
图2 GAMIT基线解算流程Fig.2 Flowchart of GAMIT baseline solution

图3 GLOBK网平差流程Fig.3 Flowchart of GLOBK adjustment

2.2 多时段并行解算设计

GAMIT/GLOBK软件以时段为基本计算单元，先依次进行基线解算，再将GAMIT基线解算结果h文件作为GLOBK的输入文件进行平差处理。将一个大规模GNSS网多时段串行解算任务分解为多个单时段并行的子任务同时进行解算，从而大幅提高基线解算效率。在并行计算过程中，所有子任务通过共享内存来访问公共数据(如tables文件)，通过进程池加锁机制来确保数据的安全性。待所有基线解算的子任务完成后，关闭主进程锁，统一进行GLOBK网平差。

设计算机核心数为C，大规模GNSS网时段数为N，进程池大小为P(最佳进程数)，则有：

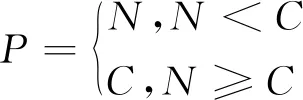
(3)

2.3 多子网并行解算设计

GAMIT/GLOBK软件是基于全基线网解的双差模型。双差网解法的计算时间会随站点数量的增加呈几何级数增大(n3)，普通计算机往往受限于性能瓶颈，难以在短时间内完成大量基线解算任务。因此，基于双差网解模型处理大规模GNSS网时，国际上比较通用的做法是首先进行分区、分子网计算，然后进行综合处理。子网划分时，选取较为稳定的一定数量站点作为子网公共基准点，以保证各子网间解算结果的连续性。后续处理流程与多时段并行解算设计类似，在此不作赘述。

同样，设计算机核心数为C，大规模GNSS网划分的子网数为M，进程池大小为P(最佳进程数)，则有：

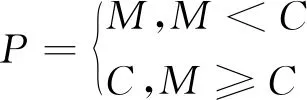
(4)

2.4 时空一体化双层并行解算

融合多时段与多子网并行2种算法，构建基于共享内存模型的时空一体化双层并行算法，实现大规模GNSS网同时在时间域(时段)和空间域(子网)两个维度上的并行化处理，使得数据处理任务完成前，任意时刻计算机所有CPU核心均被充分利用，大幅提升基线解算的时效性及CPU利用率。

设计算机逻辑核数为C，任务总数为N，最佳进程数为P，则有以下2种可能性。

1)不指定并行度。若本地计算机专门进行大规模GNSS网数据处理，为了最大限度地挖掘该计算机的算力、提高计算机的利用率，此时设计的最佳进程数P的计算公式同式(3)、(4)。

2)指定并行度S。由于本地计算机可能会处理大规模GNSS网数据工作外的其他任务，为了兼顾二者各自算力的需要，此时设计的最佳进程数P的计算公式为：

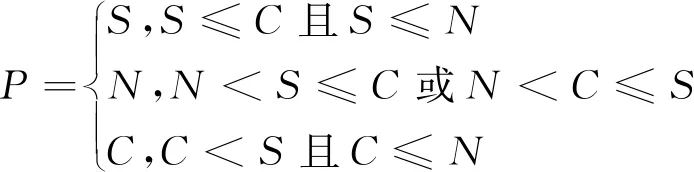
(5)

时空一体化双层并行解算设计架构如图4所示。

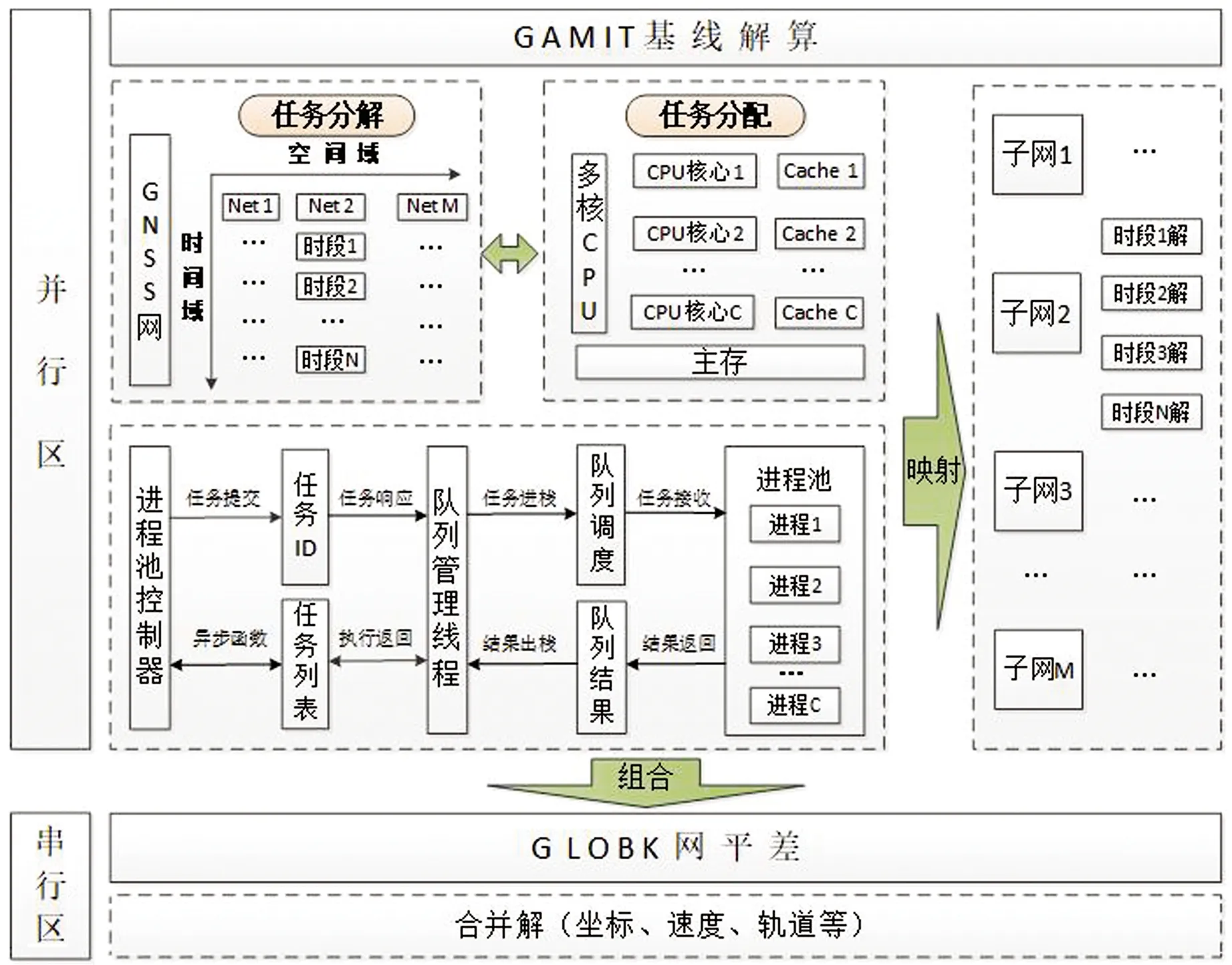
图4 时空一体化双层并行解算设计架构Fig.4 The designed architecture of spatio-temporal integration two-layer parallel solution

3 算例分析

3.1 加速比与效率测试

1)测试数据。本文收集区域内821个基准站(含IGS站)2021年doy60～90的观测数据，并将GNSS网划分为20个子网，编号为NT01～20，共组成620个时段的基线解算任务。

2)分析对比指标。本文拟采用加速比Sp和效率Ep分析对比指标。Sp可反映并行系统或并行程序的时效性和加速效果，Ep可用来衡量并行系统设备的利用率，即单位处理器的加速效果：

(6)

(7)

式中，T1为任务在单处理器下的运行时间，Tp为任务在p个处理器并行系统中的运行时间。

3)测试硬件情况。基于GAMIT/GLOBK软件，利用时空一体化双层并行算法对该大规模GNSS网进行数据处理时效性测试。测试使用的工作站硬件配置见表1。

表1 工作站硬件配置

3.2 结果分析

对测试结果进行正确性检验及统计分析。经测试，并行解算结果与传统串行模式结果一致。分别计算每个并行度(即进程数)下对应的加速比Sp、效率Ep、单时段等价串行平均用时以及单时段实际平均用时(表2、图5～7)。其中，单时段等价串行平均用时为每个并行度下实际总用时与总时段数的比值，单时段实际平均用时为每个并行度下所有时段实际总用时的平均值与总时段数的比值。每个并行度下各项指标分别独立测试3次，最终取3次测试结果的平均值。

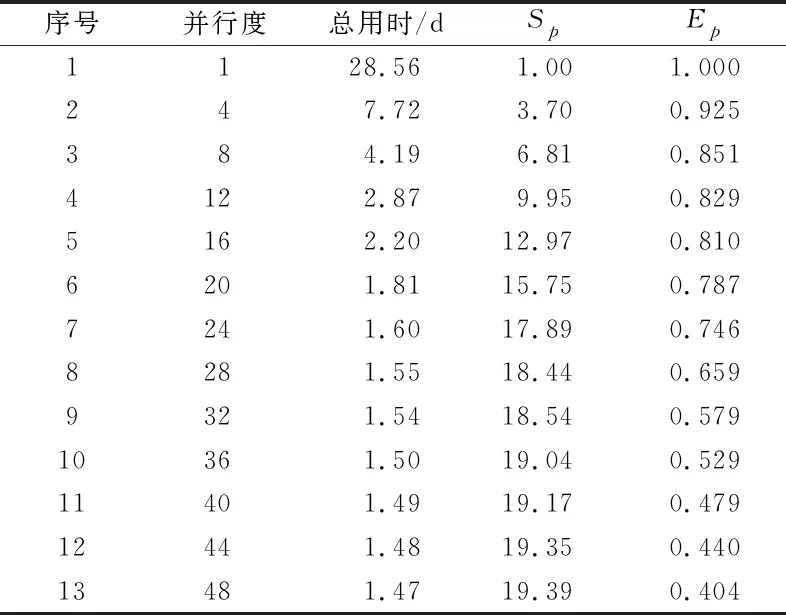
表2 不同并行度测试结果

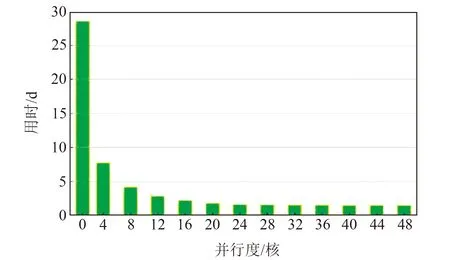
图5 不同并行度总用时Fig.5 The total time of different parallelisms

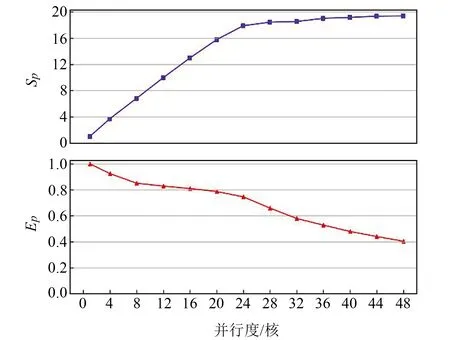
图6 不同并行度Sp与EpFig.6 The Sp and Ep of different parallelisms

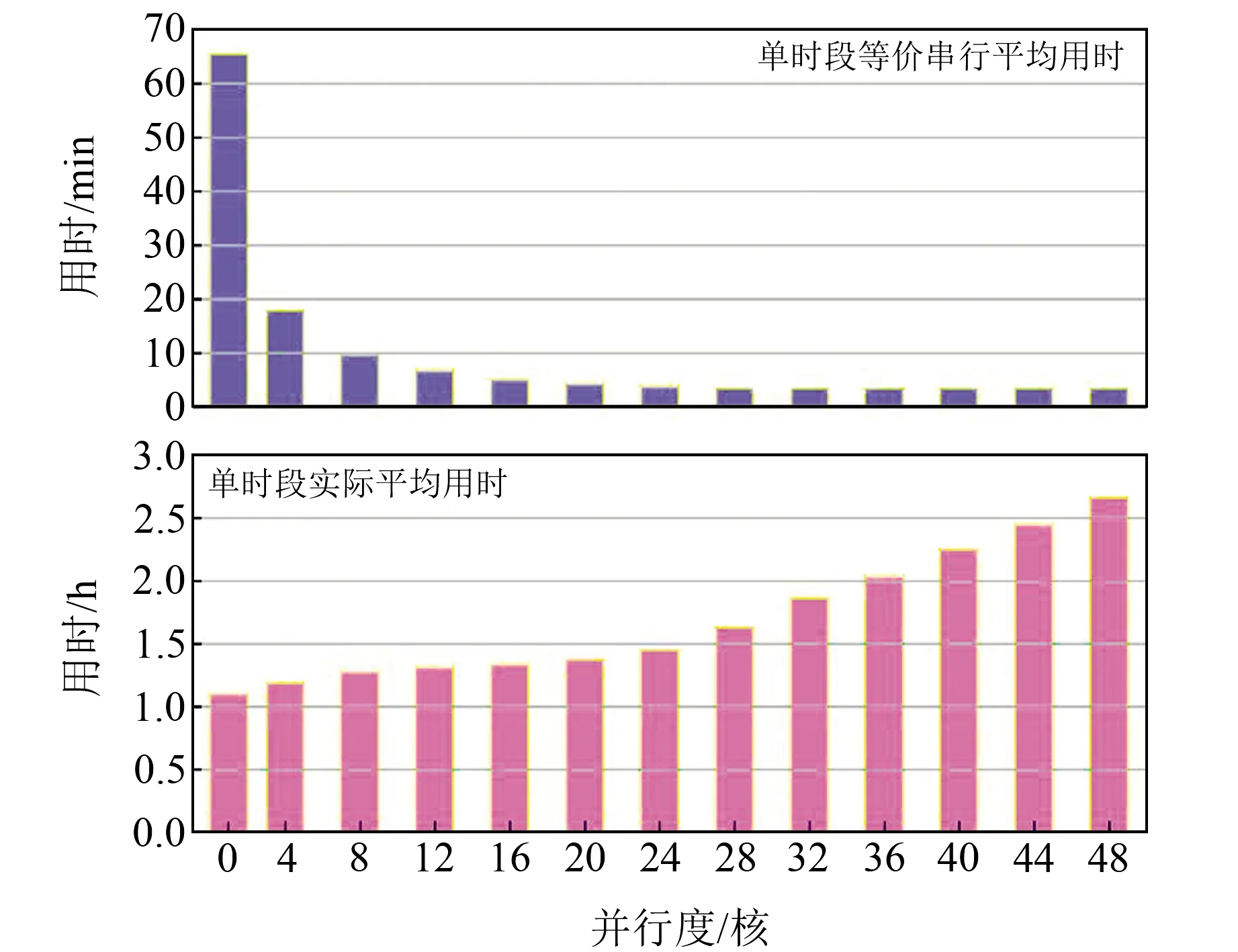
图7 单时段等价串行与单时段实际平均用时Fig.7 The equivalent serial average time and actual average time of single period

由表2和图5可知，时空一体化双层并行算法可大幅提升大规模GNSS网基线解算的时效性，基线解算总用时可从传统单进程(即单窗口)模式的28.56 d最大缩短至1～2 d。随着并行度的不断增加，基线解算总用时大幅减小，并最终趋于一个相对平稳的数值。其中，当并行度为24时，基线解算总用时达到拐点(即总用时变化率转折点)1.60 d，当并行度超过24后，总用时减少量不明显；当并行度达到测试工作站逻辑核数48时，基线解算总用时达到最小值1.47 d。由图6可知，基于时空一体化双层并行算法的加速比Sp与并行度总体呈正相关，当并行度为1～24时，Sp呈线性增加，加速效果十分显著；当并行度为24时，Sp达到拐点(即加速比增长率转折点)17.89，之后加速效果不再明显；当并行度为48时，Sp达到最大值19.39，充分验证了时空一体化并行算法的高时效性和先进性。

结合图6和图7可知，基于时空一体化双层并行算法的效率Ep与并行度呈负相关，即单位处理器的加速效果会随并行度的增加而减小。这是因为在共享内存模型下，随着并行度增大，创建进程的系统开销，如内存分配、I/O操作、任务调度等也随之增加，在一定程度上会抑制并行计算带来的性能优势，导致单位处理器整体利用率相对变小，从而使得大规模GNSS网单个时段的用时不断增加。由此可见，并行度并非越大越好，需同时考虑Sp与Ep两个因素。由于并行计算的拐点可兼顾Sp与Ep，因此在实际应用中宜选择拐点值作为时空一体化双层并行算法的最佳进程数，这样既能大幅提高基线解算的时效性，又能充分提升系统设备的利用率。

4 结 语

1)时空一体化双层并行算法可大幅提升大规模GNSS网的基线解算效率。在测试环境下，时空一体化双层并行算法的最大加速比高达19.39，相较于传统串行处理模式，其基线解算周期从28.56 d最大缩短至1～2 d，进一步验证了该并行算法的优越性和高时效性。

2)在并行系统算法设计时，应合理兼顾加速比与效率目标，并行系统的拐点可作为并行度设计的一项重要参考指标。

将本文研究成果作为算子部署在大数据环境中，利用云计算资源按需扩充、弹性配置、快速部署等优势，能更好地发挥其超算能力，优化资源配置，降低投入成本。本文设计的时空一体化双层并行算法主要针对大规模GNSS网在单节点多核环境下的基线解算场景，为充分发挥多节点集群协同作业的算力优势，基于分布式系统的多节点多核并行算法将成为下一步的研究重点。