基于双曲正切特征和双特征融合神经网络的调制方式识别

张 兆 军， 高 银 锐， 邱 天 爽， 李 芃 芃， 栾 声 扬*， 陈 薇

( 1.江苏师范大学 电气工程及自动化学院， 江苏 徐州 221116；2.大连理工大学 电子信息与电气工程学部， 辽宁 大连 116024；3.国家无线电监测中心 地面业务部， 北京 100037 )

0 引 言

调制方式识别是无线电信号检测和解调过程中不可或缺的步骤[1]，也是各类无线通信系统中至关重要的组成部分．伴随着无线通信技术的迅猛发展，调制方式识别也被广泛应用于民用以及军事领域；具体而言，其在频谱管理、电子侦察、通信对抗和认知无线电等都得到了广泛应用[2]．

调制方式识别方法大致可以归纳为两大类：第一类主要基于最大似然估计[3]，该类方法利用概率论、假设检验理论和决策准则等来解决调制方式识别问题，理论上可以获得最优结果，但是所涉及的计算量较大，计算复杂度也比较高[4]；第二类主要通过不同特征进行分类[5]，虽然该类方法理论上只能够获得次优结果[6]，但是由于其设计思路较为简单，而且计算量也较小，同时具有较多类别的特征可供选择，故而也受到学者们的广泛关注．

利用特征进行调制方式识别的方法通常以模式识别理论为基础，该类方法涉及两个重要步骤：一是无线电信号特征的选择，二是分类器的选取．将特征输入分类器就可以识别无线电信号的调制方式．通常情况下，此类方法所涉及的特征主要包括时域特征[7]、时频域特征[8]、二阶或者高阶统计量特征[9]、循环频率域特征[10]、星座图[11]以及极坐标图[12]等．

伴随着机器学习理论的迅猛发展，学者们提出了诸多分类器，主要包括决策树[2]、随机森林[13]、K最近邻[14]、支持向量机[5]以及各类神经网络[9]等．作为机器学习的一个重要分支，深度神经网络也获得了广泛关注，卷积神经网络(CNN)、循环神经网络(RNN)和生成对抗网络(GAN)逐渐成为主流的模式识别分类器；此外，变换网络(transformer)也引起了学者们的兴趣，故而上述各类深度神经网络也被用于解决调制方式识别的问题．

以卷积神经网络为例，文献[15]利用Choi-Williams分布获得二维时频分布矩阵，并将其作为深度残差收缩网络(DRSN)的输入进行分类．由于此类网络提取分类特征的能力较强，故而该方法能取得较高的识别准确率．以循环神经网络为例，文献[16]利用两层的长短期记忆网络(LSTM)对IQ信号的幅度和相位特征进行分类，也能取得较好的识别结果．以变换网络为例，文献[17]将自然语言处理(NLP)方向的自注意力机制引入神经网络，用来对调制方式进行识别，同样取得了较为准确的识别结果．

此外，还有学者基于不同类型的基础神经网络设计了复合神经网络，以期克服单一神经网络自身的缺陷．举例而言，文献[18]以串联方式组合了卷积神经网络和双向长短期记忆网络(BiLSTM)，并提出了CNN-BiLSTM网络作为分类器．文献[8]选取IQ信号和对应的时频矩阵作为特征，分别输入并联的循环神经网络和卷积神经网络，以实现调制方式识别．

上述基于深度神经网络的调制方式识别方法主要选取RML2016.10a或者RML2016.10b作为数据集[8，15-16，18]，而且此实验条件下，上述方法均取得了较高的识别准确率．在该数据集中，噪声被假设为高斯噪声，这是一类具有代表性的噪声；但是这种假设也有一定的局限性，因为在自然界以及人类社会中，海杂波、闪电和汽车点火等因素都会在噪声中引入较大的野点(outlier)，故而导致噪声具有脉冲性[19]．从幅度特性来看，该类噪声中存在尖锐的峰值；从统计特性来看，该类噪声的概率密度具有较厚的拖尾(heavy tails)，故而该类噪声是一类典型的非高斯噪声．由于高斯噪声和以脉冲性噪声为代表的非高斯噪声都是常见的噪声类型，故而混合噪声条件下的调制方式识别方法也应该得到重视．

而在混合噪声条件下，由于噪声模型不匹配，许多现存的调制方式识别方法都会产生性能退化的问题，甚至会出现完全失效的情况．为了解决此类问题，本文提出一种新的基于特征的调制方式识别方法．与传统方法不同，本方法首先利用双曲正切(hyperbolic tangent)函数对IQ信号进行预处理，进而提出两类新的特征，分别是双曲正切星座图(hyperbolic-tangent-based constellation，HT-COST)以及双曲正切IQ信号(hyperbolic-tangent-based IQ，HT-IQ)．然后，基于注意力机制和门控循环单元等，本方法设计一种双特征融合的深度神经网络作为分类器．将预处理后所提取的两类特征分别输入该分类器的两支，就可以获得调制方式的识别结果．

为了验证所提出特征的鲁棒性以及双特征融合分类器的性能，本文首先在两种不同的混合噪声条件下进行3组共6项实验，分别对比不同识别方法、不同特征组合以及不同网络的识别准确率；此外，本文还进行2组实验，分别比较不同网络结构的计算复杂度和不同方法的运行时间．

1 基础理论

1.1 系统模型

本文提出的调制方式识别方法的系统模型如图1所示．其中，信号模型为

y(t)=x(t)+v(t)

(1)

式中：x(t)和y(t)分别为发射和接收的信号，v(t)为服从高斯分布和Alpha稳定分布的混合噪声，t为连续时间变量．

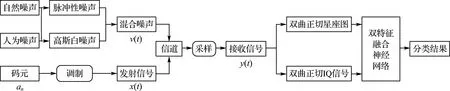
图1 系统模型

1.2 Alpha稳定分布噪声

本文采用Alpha稳定分布来描述脉冲性噪声这一类典型的非高斯噪声．若随机变量X服从Alpha稳定分布，则其特征函数的表达式为

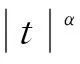
(2)

式中：α∈(0，2]表示特征指数，β∈(-1，1)表示对称参数，γ表示分散系数，μ表示位置参数．sgn(t)表示符号函数，ω(t，α)的表达式为

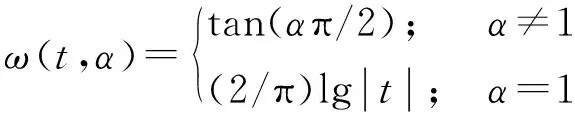
(3)

本文采用广义信噪比G来衡量信号和噪声的强度之比，其定义式为

(4)

其中Ps表示信号的功率．

2 调制方式识别方法

2.1 方法流程

本文所提出的调制方式识别方法可以概括为两个步骤：特征选择和分类器选取．首先使用双曲正切函数预处理IQ信号，再通过计算获得双曲正切星座图和双曲正切IQ信号，这两种特征分别为图像和序列．然后，将双曲正切星座图作为双特征融合神经网络一条支路的输入，将双曲正切IQ信号作为另一条支路的输入，对11种调制信号进行分类．调制方式识别方法流程如图2所示．

2.2 双曲正切星座图和双曲正切IQ信号

对接收到的信号y(t)进行采样，获得复序列y(n)，使用双曲正切函数对该复序列进行非线性映射．具体公式为

yHT(n)=tanh(y(n))=aHT(n)+jbHT(n)

(5)

式中：aHT(n)表示双曲正切I路信号，bHT(n)表示双曲正切Q路信号，再以(aHT(n)，bHT(n))为坐标进行标记，即可获得双曲正切星座图．根据RML2016.10a数据集[14]，本文所选取的11种调制信号的双曲正切星座图如图3所示．

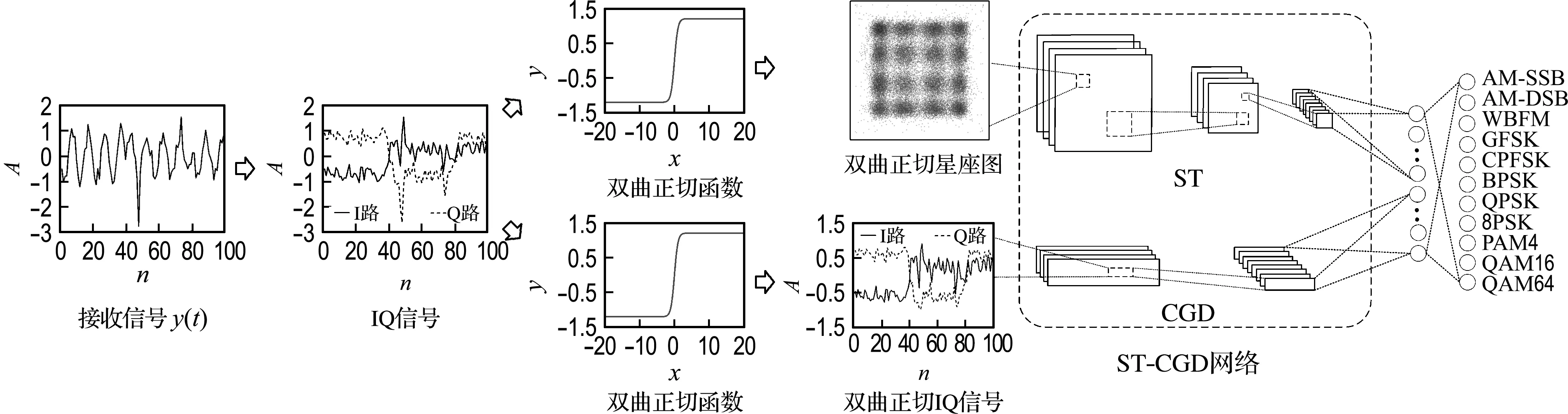
图2 调制方式识别方法流程

图3 RML2016.10a中11种调制信号的双曲正切星座图

2.3 双特征融合神经网络

在设计双特征融合神经网络时，需要同时考虑它的分类准确率和计算复杂度．首先，双特征融合网络的一条支路借助于混合单元(shuffle unit)[20]取得较低的计算复杂度，并通过变换网络(transformer)[21]引入注意力机制，故而简称为ST路．然后，另一条支路借助于卷积层(convolution layer)获得较强的特征提取能力，再利用门控循环单元(gated recurrent unit，GRU)引入注意力机制，最后经过稠密层(dense layer)进行分类，故而简称为CGD路．为了方便描述，在后续章节中，该双特征融合网络也被称为ST-CGD网络．ST-CGD 网络的具体结构设置参见图4．

如图4所示，ST路由卷积层、混合单元、多头注意力(multi-head attention)、多层感知机(multilayer perceptron，MLP)以及全连接层(fully connected layer，FC)构成．首先，由卷积层进行初步的特征提取并缩小特征尺寸，然后使用非线性激活函数引入非线性映射，增强模型的表达能力．其次，混合单元通过双分支结构对输入进行不同层次的特征提取，并使用通道混合操作来增强通道间的信息交流，进而将获得的特征图分割成块，并通过位置编码来形成序列式的特征，由多头注意力模块在不同子空间中计算注意力权重，再将权重信息进行合并，从而提升注意力机制的效果．最后，通过全连接层和激活函数构成的多层感知机进一步增强模型的表达能力．

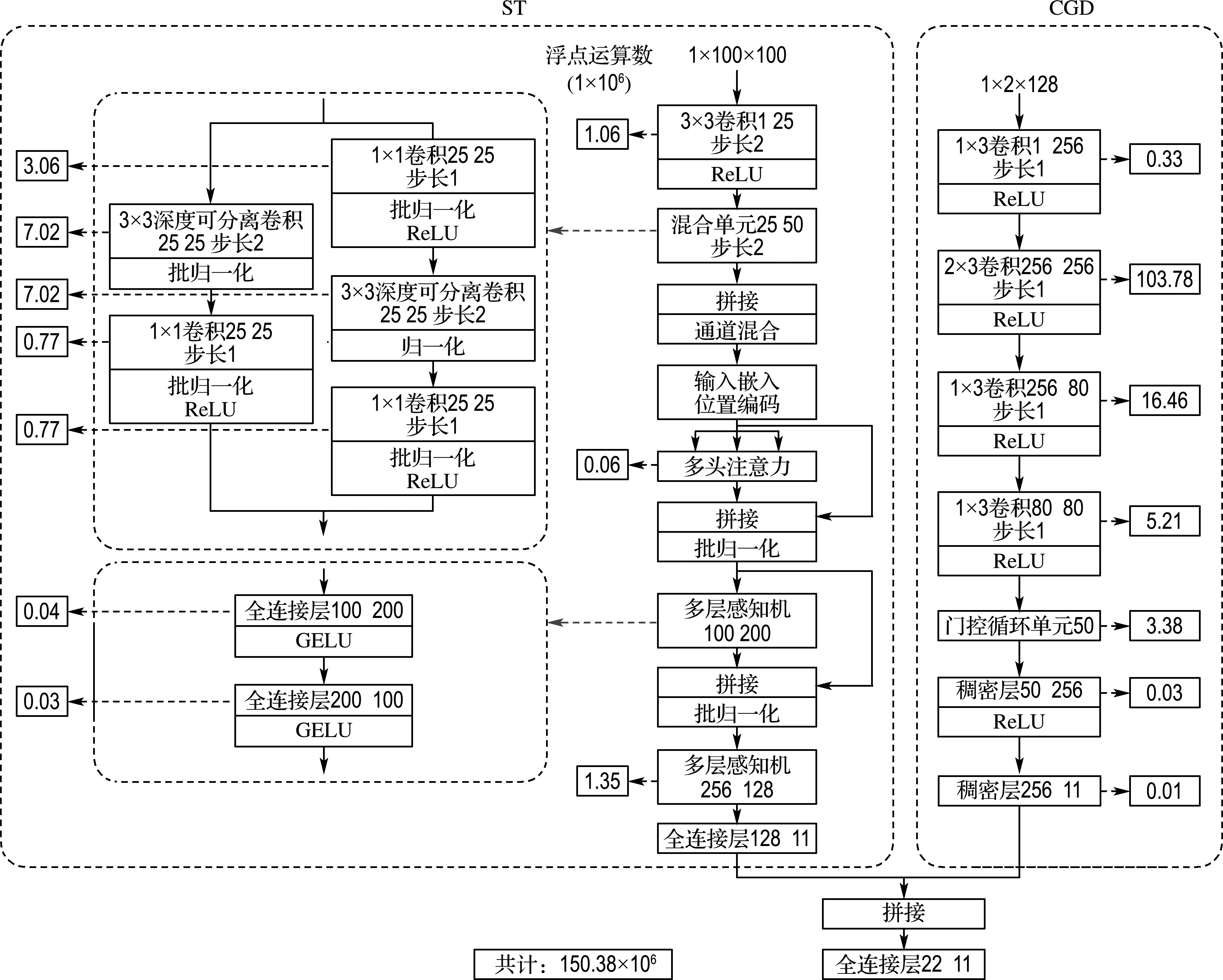
图4 双特征融合神经网络(ST-CGD)的结构以及计算复杂度

而CGD路由卷积层、门控循环单元和稠密层堆叠而成．首先，由1×3和2×3的非对称卷积对序列数据进行特征提取，进而通过门控循环单元获取输入特征中的关键信息以及相互的关联性．然后，使用稠密层进行分类．最终，在ST路和CGD路的末端进行特征融合，该位置的融合操作能够充分保留两个分支网络所提取的特征，同时进一步增强双特征融合神经网络的特征提取和泛化能力．

3 仿真实验和结果分析

3.1 实验平台

本文的硬件实验平台为英特尔酷睿i7-6700 3.4 GHz处理器、32 GB内存、1 TB固态硬盘和英伟达RTX 1070 8 GB显卡，软件实验平台为Windows 10操作系统以及Python、Pytorch、Pycharm．

3.2 信号、噪声和数据集

根据RML2016.10a数据集[14]，选取11种不同的调制信号，分别是AM-SSB、AM-DSB、WBFM、GFSK、CPFSK、BPSK、QPSK、8PSK、PAM4、QAM16和QAM64．然后分别添加高斯白噪声和脉冲性噪声，高斯白噪声的信噪比取值和脉冲性噪声的广义信噪比一致，混合噪声条件分别设置如下：当特征指数α为1.5时，广义信噪比G的取值范围为[-20，20] dB；当广义信噪比为5 dB时，特征指数α的取值范围为[1，2]．针对不同的调制信号和噪声条件各生成1 000个样本，将现有样本充分混合后，再按照8∶2的比例生成训练集和测试集．

3.3 实验条件和评价标准

训练过程中使用AdamW优化算法和分类交叉熵损失函数(categorical crossentropy)，学习率设置为0.001．本文方法和对比方法都进行了10次的蒙特卡罗实验，并取均值作为实验结果．

本文采用识别准确率Pacc来衡量算法的性能，其定义式为

Pacc=Nacc/N

(6)

式中：Nacc表示被准确识别的样本数目，N表示总的样本数目．

3.4 仿真实验

实验1不同调制方式识别方法的对比

本实验比较了12种不同方法的识别准确率，这些方法分别是本文方法、ST、CGD、CNN2[22]、LSTM2[22]、CLDNN[22]、决策树[14]、K最近邻[14]、随机森林[23]、支持向量机[14]、深度神经网络[14]和梯度提升决策树．ST使用的特征为双曲正切星座图，CGD使用的特征为双曲正切IQ信号，其他方法参考文献[14，22-23]设定特征．当广义信噪比改变时或特征指数改变时，各种方法的识别准确率分别如图5、6所示．

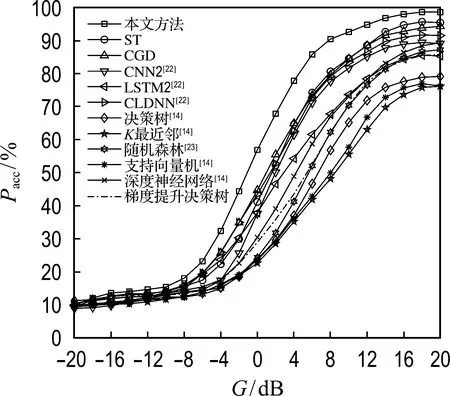
图5 不同调制方式识别方法的识别准确率曲线(α=1.5)

如图5所示，当广义信噪比增加时，12种方法的识别准确率都出现了较大幅度的提升，这表明噪声的强弱会对各类调制方式识别方法的性能产生显著影响．当广义信噪比为[-6，20] dB时，相较于其他方法，本文方法有明显的准确率优势．同时，本文方法优于ST和CGD，说明本文所提出的双特征融合策略的有效性．此外，ST、CGD、CNN2、LSTM2和CLDNN等深度学习方法的识别准确率总体上优于其他机器学习方法，说明了深度学习神经网络具有良好的分类性能．

如图6所示，当特征指数增加时，12种方法的识别准确率都呈现出了较为平缓的上升趋势，这表明噪声的脉冲性强弱也会对各类调制方式识别方法的性能产生影响，但相较于广义信噪比，这种影响相对较小．在本实验的所有条件下，本文方法均展现出了明显的准确率优势，故而验证了本文所提方法对于混合噪声的鲁棒性．

实验2不同特征组合的对比

本实验比较了不同特征组合所对应的识别准确率，共涉及5类特征以及6种组合，特征分别是双曲正切星座图、双曲正切IQ信号、分数低阶星座图[24]、星座图和IQ信号．本实验以ST-CGD网络作为分类器，当广义信噪比改变或特征指数改变时，不同特征组合的识别准确率分别如图7、8所示，图例中说明了所采用的特征组合．

如图7所示，双曲正切特征的组合具有最高的识别准确率．当广义信噪比较高时，双曲正切星座图+IQ信号组合的准确率低于上述特征组合，说明了双曲正切IQ信号能够有效抑制混合噪声中的野点；而当广义信噪比较低时，两类特征组合的准确率差别较小，说明当噪声过于恶劣时，各类特征均出现了性能退化．此外，准确率最高的两类组合都使用了双曲正切星座图，进一步验证了该特征对于混合噪声的鲁棒性．而其他特征组合的准确率均低于本文所提出的特征组合的准确率，这验证了本文所提出的特征在抑制混合噪声方面的优势．

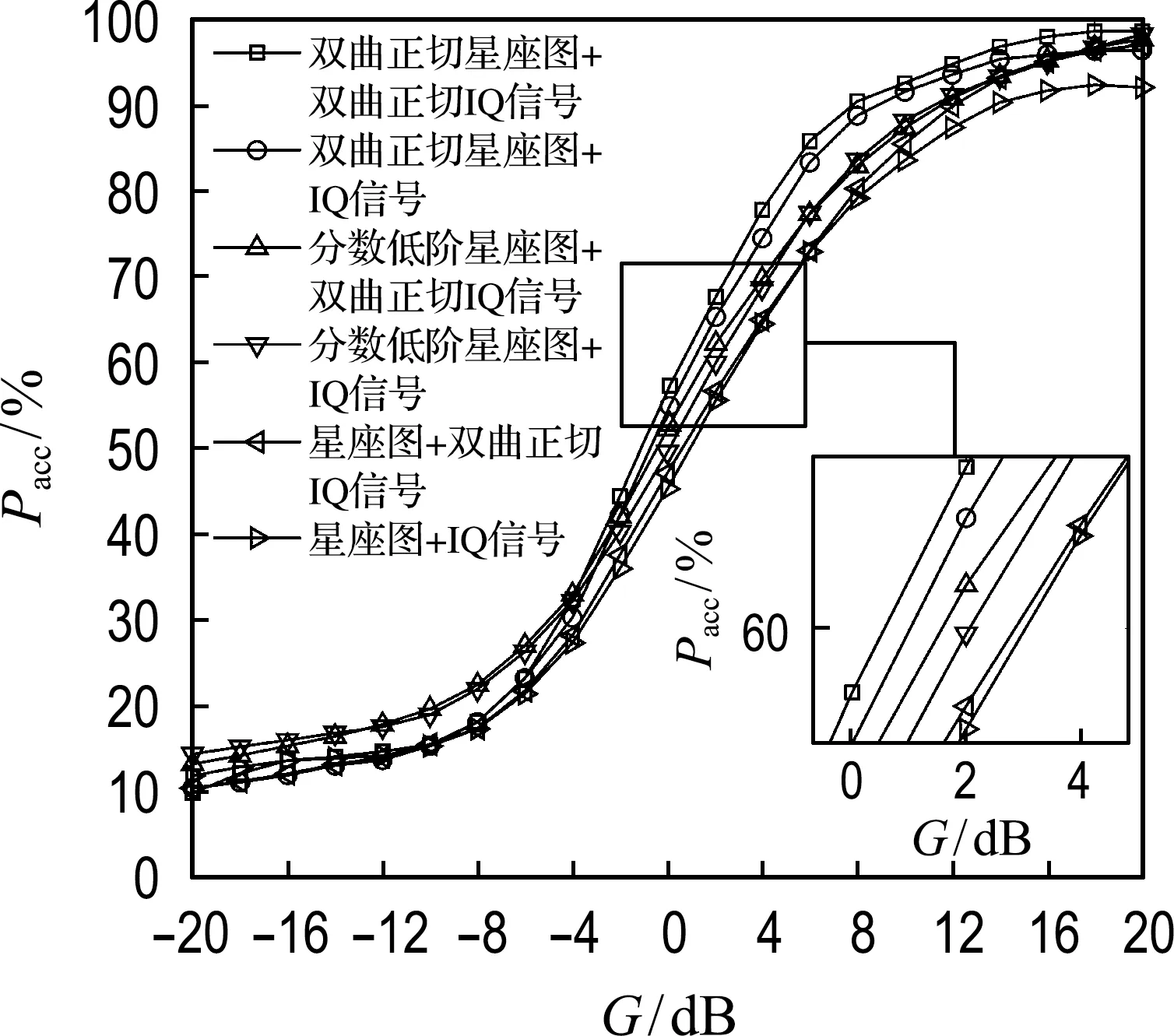
图7 不同特征组合的识别准确率曲线(α=1.5)

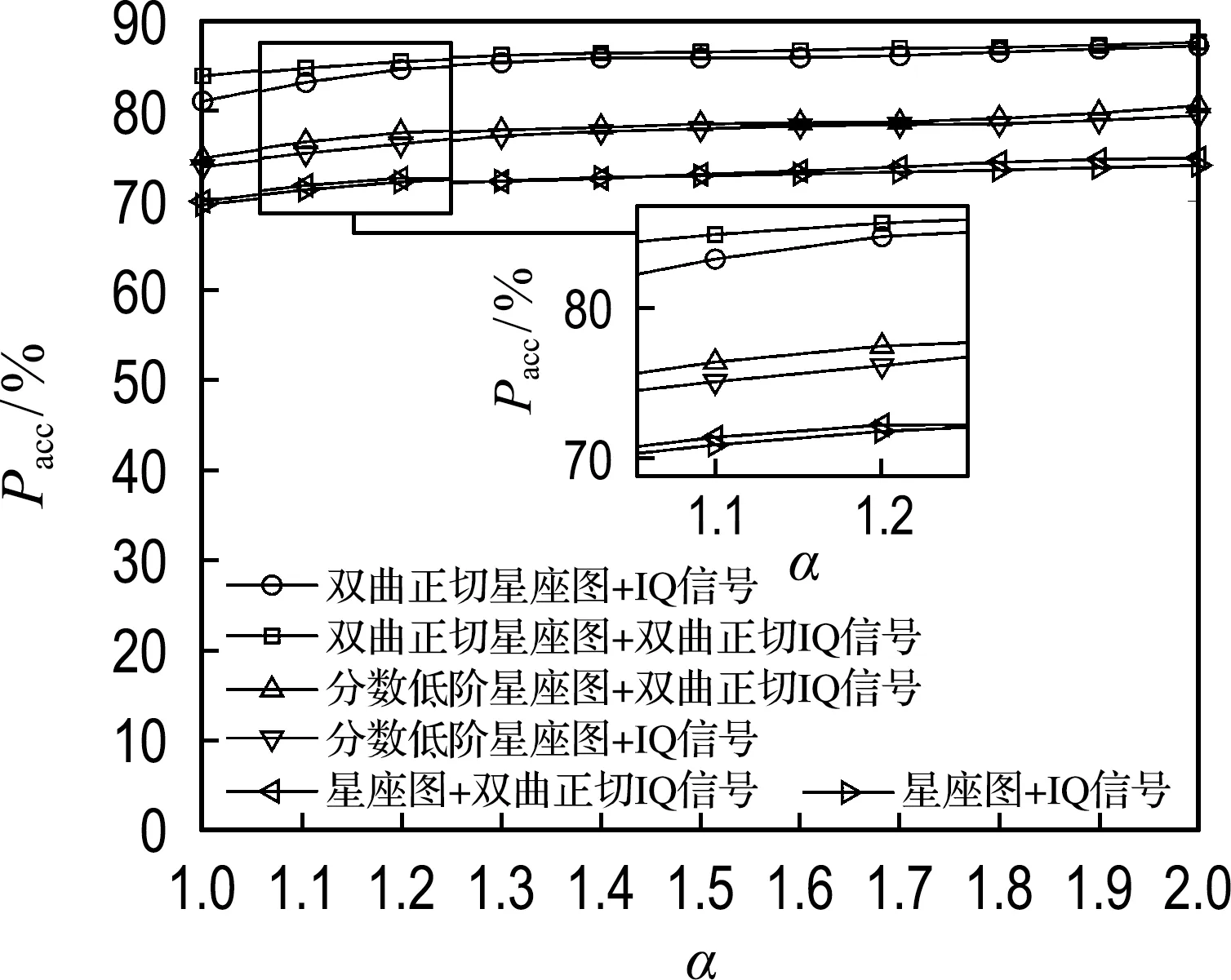
图8 不同特征组合的识别准确率曲线(G=5 dB)

与图7的现象相似，图8中选用双曲正切星座图作为特征的两种方法具有最高的识别准确率，说明该特征能够有效克服混合噪声的影响．此外，当特征指数逐渐变小，即噪声的脉冲性逐渐增强时，上述两种方法的准确率差距逐渐变大，进一步说明了相较于IQ信号，双曲正切IQ信号能够抑制这种脉冲性．此外，其他特征组合的准确率较低，说明了其抑制混合噪声的能力较弱．

实验3不同网络的对比

由图5可知，相较于双曲正切IQ信号和CGD单路网络的组合，双曲正切星座图和ST单路网络的组合能够获得更高的准确率，故而这种特征和单路网络的组合对双特征融合网络的准确率贡献更大．上述结论同样体现在了实验2的结果中，即当双曲正切星座图特征被替换为分数低阶星座图或星座图后，即使另一支路仍采用双曲正切IQ信号和CGD网络，整体的准确率也会显著降低．

在本实验中，当图4中右路的特征固定为双曲正切IQ信号，网络固定为CGD网络时，左路的特征分别选取双曲正切星座图、分数低阶星座图和星座图，网络分别选取ST、ResNet[25]和ShuffleNet V2[20]．对不同的特征和分类器组合的识别准确率进行比较，不同噪声条件下的实验结果分别如图9、10所示，图例中说明了左路特征和网络．

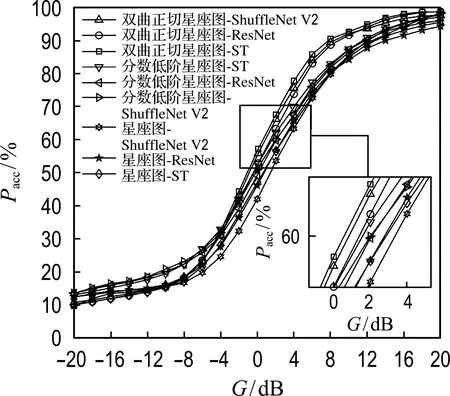
图9 不同网络的识别准确率曲线(α=1.5)

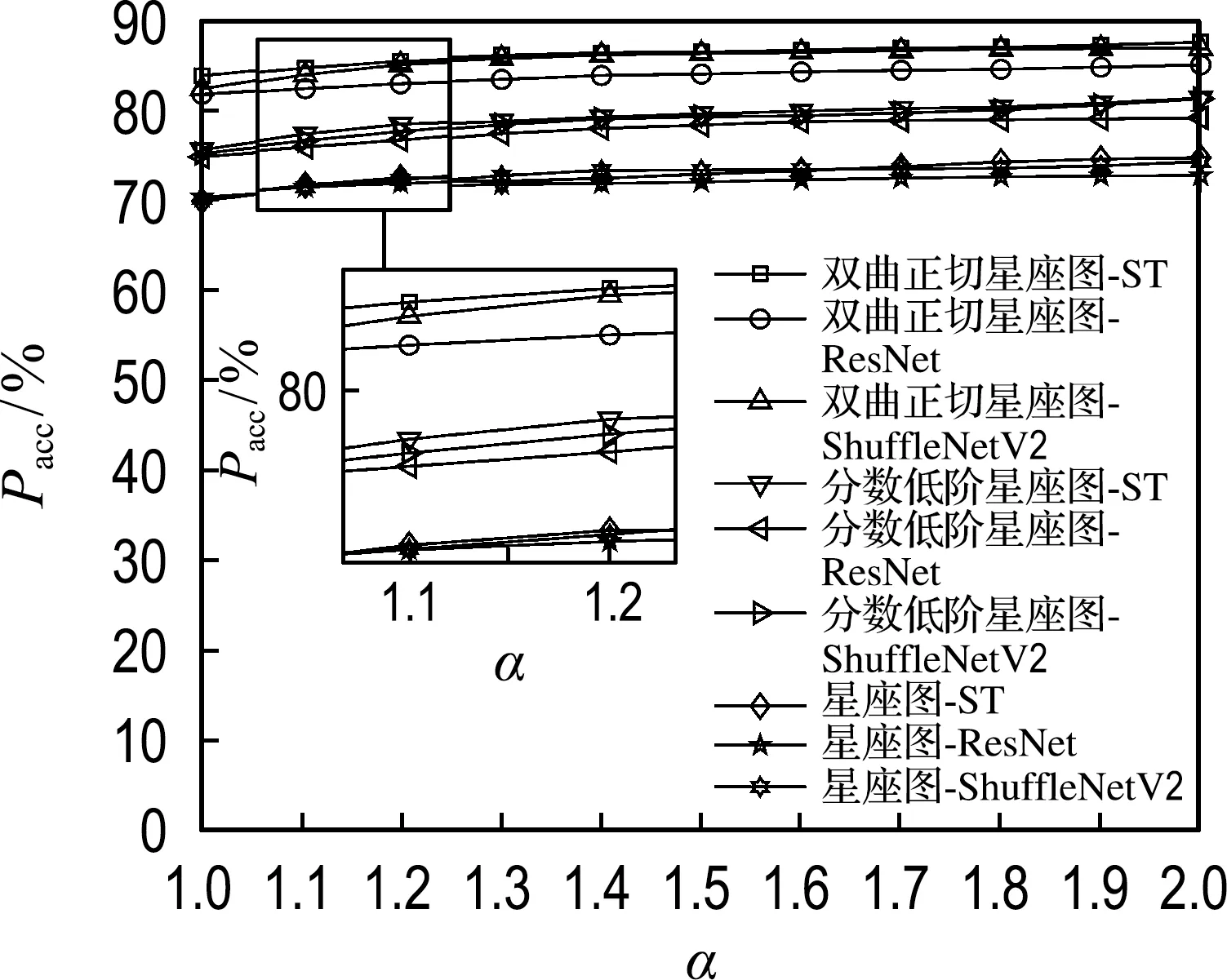
图10 不同网络的识别准确率曲线(G=5 dB)

如图9所示，若选取双曲正切星座图作为特征，当广义信噪比较高时，相较于ResNet-CGD和ShuffleNet V2-CGD，ST-CGD有识别准确率优势；而当广义信噪比较低时，各网络的分类性能均出现了严重退化．若选取分数低阶星座图或星座图作为特征，并结合表1可知，上述3类网络的总体识别准确率较为接近，但ST-CGD仍略优于其他网络．上述结果表明，在处理不同特征时，本文所提出的ST-CGD具有较为优秀的分类性能．

由图10和表1同样可知，当特征固定时，ST-CGD在3类网络结构中能够保持准确率优势，从而说明了其具有较好的分类性能．

实验4计算复杂度

本实验通过浮点运算数[26]来衡量模型的计算复杂度，文中所涉及的9种神经网络的计算复杂度如表2所示．

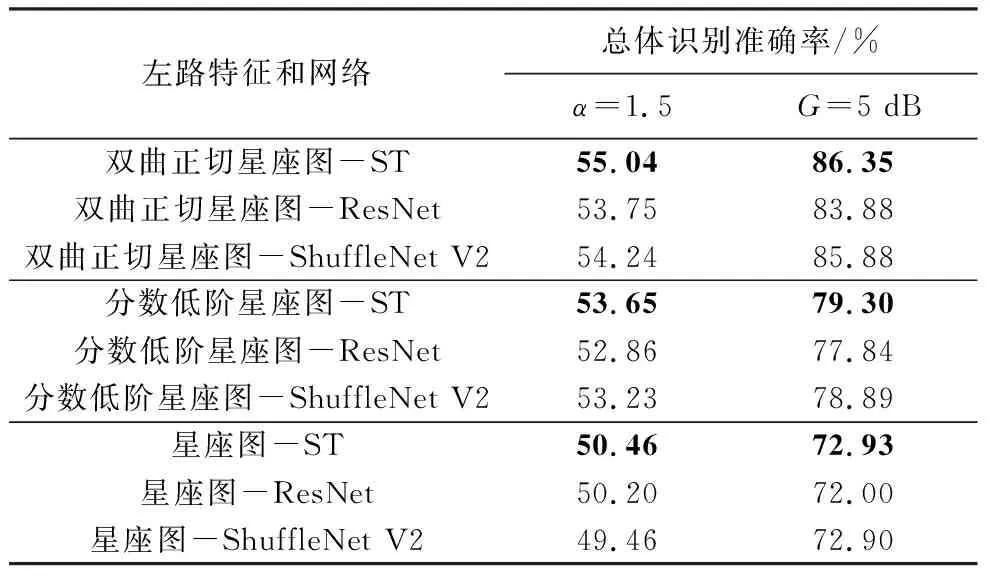
表1 不同网络的总体识别准确率

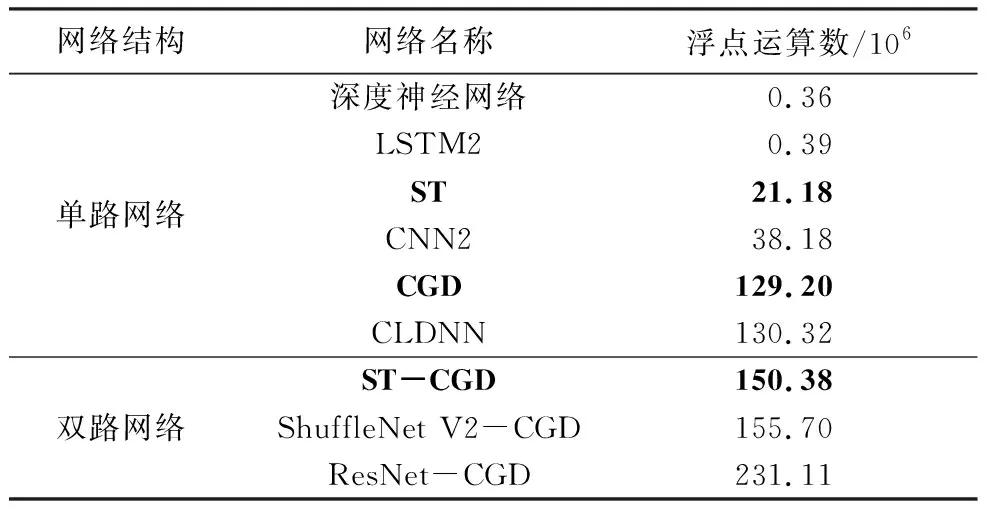
表2 深度神经网络的计算复杂度

如表2所示，就单路网络而言，ST具有第三小的计算复杂度，CGD则处于第五位；而由图5可知，相比于其他单路网络，这两类网络具有最高和第二高的识别准确率．就双路网络而言，ST-CGD具有最小的计算复杂度；同时，由表1可知，对于3类星座图特征，该双路网络均具有最高的识别准确率．

综上所述，本文所设计的网络在保证分类性能的前提下，结构也较为简单．

实验5运行时间

除了计算复杂度，本实验还将比较不同方法的运行耗时．对整个测试集所有样本进行一轮分类所需的运行时间如表3所示．

由表3可知，传统的机器学习方法占据了最小运算耗时的前四名，而CGD和ST分别取得第五名和第七名；但是就分类性能而言，CGD和ST的识别准确率远高于前四者；此外，ST-CGD的运行耗时约为两个单路网络的耗时之和，但其具有最好的识别准确率，由此可知，双路网络以运行耗时为代价提升了准确率．而随着计算机运算能力的不断提升，这种代价是可接受的．

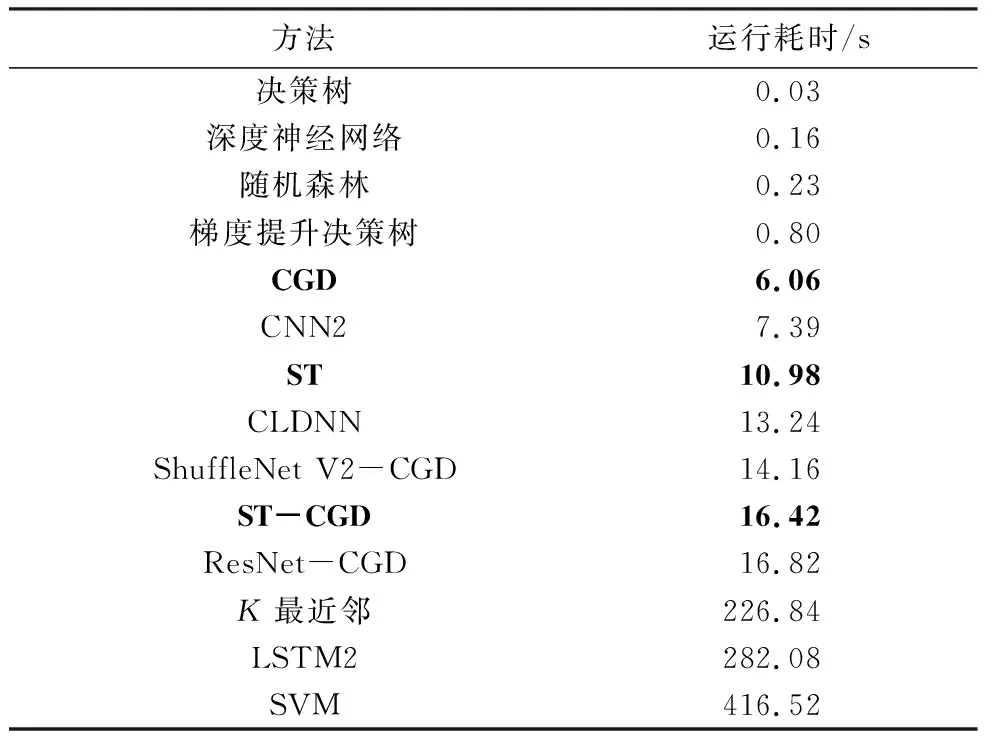
表3 调制方式识别方法的运行时间

4 结 语

对于混合噪声条件下的调制方式识别问题，本文首先提出了双曲正切星座图和双曲正切IQ信号作为特征．其次，基于注意力机制和门控循环单元等设计了ST-CGD双特征融合神经网络作为分类器．然后，在两种不同的混合噪声条件下，从不同识别方法、不同特征组合和不同网络等方面对识别准确率进行了对比．最后，本文还对不同网络结构的计算复杂度以及不同方法的运行时间进行了统计和对比．仿真结果表明，本文方法对于混合噪声条件下的调制方式识别问题能够取得良好的效果．