连续卸船机取料装置换舱路径规划研究
2023-02-03王欣,刘雪莲,姜鑫,于效民
王 欣, 刘 雪 莲, 姜 鑫, 于 效 民
( 1.大连理工大学 机械工程学院,辽宁 大连 116024;2.大连华锐重工集团股份有限公司, 辽宁 大连 116013 )
0 引 言
随着码头建设大型化、专业化的发展,以及科学技术的不断进步,港口装备设计制造水平不断提高,卸船设备也在不断更新换代[1].链斗式连续卸船机(以下简称连续卸船机)凭借环保、节能、高效等特点,将逐步取代抓斗卸船机,成为未来卸船机的发展趋势.现阶段,连续卸船机的操作方式是司机在司机室内手动操作完成卸船过程,存在卸船效率低及安全性问题.连续卸船机自动化和无人化取料是其未来的发展方向,本文对连续卸船机取料装置进行路径规划研究,保证取料装置在不与船舱发生碰撞的前提下找到较短的安全路径,为实现连续卸船机智能化取料提供理论基础,对提高卸船效率、降低卸船成本、缩短船舶停港时间具有重要意义.
传统的路径规划算法需要对障碍物进行建模和描述,不适用于高维的路径规划问题.与传统的路径规划算法不同,基于采样的路径规划算法是在工作空间内进行随机采样并对采样点进行碰撞检测,进而获得可行采样点,能够避免空间建模,有效解决高维空间和复杂约束的路径规划问题[2].基于采样的路径规划算法主要包括概率地图(PRM)算法[3]、快速扩展随机树(RRT)算法[4]等.PRM算法在解决三维空间路径规划问题时采样点的数量过多,收敛速度慢;RRT算法由LaValle 于1998年正式提出,该算法具有概率完备性且收敛速度快,高维空间路径规划效率较高,能够在有障碍物的环境下较快地找到一条可行路径,因此,适用于连续卸船机取料装置的路径规划研究.但RRT算法基于随机采样,所以规划出的路径具有随机性,可能并不是最优路径,并且路径质量与采样点以及随机步长等参数有关.基于以上问题,学者基于传统RRT算法提出了许多改进的RRT算法,例如Bi-RRT算法(双向快速扩展随机树算法)[5],在传统RRT算法的基础上进行双向扩展,同时将起点和终点作为根节点生成两棵树,直至两棵树连接生成一条可行路径,使搜索效率大大提高.在此基础上,基于双向扩展平衡的联结型双树RRT算法,即RRT Connect算法被提出,在双向扩展随机树的基础上增加贪婪策略,当生长叶节点不与采样环境中的障碍物发生碰撞时,则继续朝向该方向采样,减少了对空白区域的无用搜索,大大加快了搜索速度,减少了搜索时间.Karaman等提出RRT*算法[6],将渐近最优思想加入算法中,采用对父节点进行重新选择和重新布线操作来寻找较优路径.王坤等[7]通过引入智能采样函数和快速扩展策略,在渐近最优双向扩展随机树算法的基础上提出EB-RRT*算法,并将改进后的算法应用于移动机器人的无碰路径规划研究.该算法大大提高了算法的扩展效率,同时能有效避免算法易陷入局部最优的问题.陈满意等[8]将低振荡人工势场法与自适应快速扩展随机树算法相结合,提出ARRT混合算法,该算法能够较好地适用于多障碍物环境,并且使路径平均搜索时间大大减少,但是该算法只针对静态环境,不适用于动态环境的路径规划问题.彭鹏等[9]在传统RRT算法基础上对采样点的产生数量进行改进并加入目标偏置策略,同时,对人工势场法中的引力场和斥力场进行重新定义,将改进后的RRT算法与改进后的人工势场法结合,提出APF-RRT算法,该算法能够适用于解决具有动态障碍物的路径规划问题.
本文主要针对传统RRT算法导向性差、收敛速度慢、路径质量差等问题进行改进,将改进后的算法应用在连续卸船机换舱路径规划研究中.首先,为提高RRT算法的收敛速度,在双向RRT基础上进行改进,结合连续卸船机实际作业情况,对采样点进行智能约束;为提高RRT算法导向性,引入概率偏置因子,将目标点以一定的概率作为采样点,从而使树的扩展具有方向性;为提高路径质量,将渐近最优的思想代入算法中,对父节点进行重新选择和重新布线操作,使路径长度更短;在得到初始路径后,采用粒子群算法对路径的长度和平滑度进行优化;最后采用贝塞尔曲线对路径进行平滑处理,得到最终路径.在连续卸船机实际工作中,由于载货量较大,货船受海浪影响较小,为保证连续卸船机的安全运行,在进行路径规划时将货船舱口作为障碍物并对其进行膨胀处理,从而保证规划出的路径安全可靠.
1 连续卸船机作业过程分析
链斗式连续卸船机具体结构如图1所示,连续卸船机的关键动作主要包括卸船机整车行走、臂架回转、臂架俯仰、BE回转(筒体提升系统回转).其中,BE回转主要实现连续卸船机取料装置的旋转.连续卸船机在对大型货船进行取料时,由于载货量较大,运输船一般具有多个舱口.以某钢厂原料码头靠泊作业的智达2.3×105t散货船为例,舱口布局如图2所示.在实际卸载过程中,综合码头实际卸载条件,采用了3台卸船机进行协同取料,考虑船体平衡,当各船舱内物料减载到一定吨位后,卸船机需换舱作业.根据整船减载工艺,A卸船机负责1、2、3舱内物料卸载,B卸船机负责4、5、6舱内物料卸载,C卸船机负责7、8、9舱内物料卸载.第1阶段,A卸船机减载2舱、B卸船机减载5舱、C卸船机减载8舱,3台卸船机同时工作,对舱内物料进行卸载,减载至目标量后,完成第1阶段取料.第2阶段,A卸船机移出2舱到3舱取料、B卸船机移出5舱到6舱取料、C卸船机移出8舱到9舱取料,如图2所示.整船卸载流程如表1所示.要实现整船卸载,卸船机需要完成多次换舱作业,而且实际卸船过程中,受海上和作业环境的影响,还会存在动态调整换舱顺序的可能.显然,卸船机在整个卸船过程中包括频繁的换舱操作,对连续卸船机取料装置进行换舱路径规划研究将有助于提高整体作业效率,实现卸船机无人化作业.

图1 链斗式连续卸船机结构图
目前,针对连续卸船机取料装置的路径规划研究较少,为此,本文对连续卸船机的整个卸船过程进行分析,采用改进RRT算法对换舱路径进行规划,为实现连续卸船机无人化作业提供理论基础.

图2 船舱布局及卸船顺序示意图

表1 整船卸载流程
2 换舱路径规划算法研究
2.1 RRT算法原理
RRT算法是基于采样的路径规划算法[10],通过在采样空间进行采样的方式对随机树进行扩展,从而生成一条连接起点与终点的可行无碰路径,算法的基本流程如下:
(1)初始化随机树T,将起点Xinit加入随机树T中,作为随机树的根节点.
(2)在采样空间产生一个随机点Xrand,遍历已有节点,将Xrand与随机树T中距离Xrand最近的节点Xnear连接.
(3)以一定步长Lsegm在向量(XnearXrand)方向上截取得到新节点Xnew,连接节点Xnear、Xnew.
(4)对新节点Xnew进行碰撞检测,若Xnew与Xnear的连线与环境中障碍物未发生碰撞,则将新节点Xnew加入随机树T中,若发生碰撞,则舍弃Xnew这个节点,继续执行步骤(2).
(5)判断新节点Xnew与目标点Xgoal之间的距离是否小于步长Lsegm,若小于,则进行碰撞检测,如果不发生碰撞,则将新节点Xnew与目标点Xgoal直接连接,否则继续.
(6)重复步骤(2)~(5),直至目标点Xgoal被添加到随机树T中.
快速扩展随机树的过程如图3所示.

图3 快速扩展随机树过程示意图
传统RRT算法存在搜索效率低的问题,为了提高算法的搜索效率,LaValle和Kuffner提出了Bi-RRT算法.Bi-RRT算法从起点和目标点同时扩展两棵树,树的扩展过程与传统RRT算法相同.在树的生长过程中依次循环遍历两棵树上已有的叶子节点,直至两棵树存在叶子节点之间的距离小于一定值时,连接生成一条可行路径.该算法通过双向扩展的方式提高算法的效率.Bi-RRT算法扩展过程如图4所示.

图4 双向快速扩展随机树过程图
Bi-RRT算法采用双向扩展的方式一定程度上解决了传统RRT算法搜索效率低的问题,但是该算法还存在以下问题:
(1)算法存在随机性.基于采样的算法都是在寻路空间进行随机采样,这就导致同一算法前后所规划路径具有随机性.
(2)导向性差.Bi-RRT算法在扩展节点时不会有目的地向目标点方向扩展,在远离目标点方向、寻路空间边缘位置以及障碍物边缘都会产生大量的随机采样点[11].
(3)稳定性差.采用该算法解决同一路径规划问题时,前后规划出的路径情况可能大不相同.Bi-RRT算法是概率完备但非最优的,每次规划都能够找到可行路径但是并非最优路径.
(4)规划出的路径质量差.Bi-RRT算法与传统RRT算法相同,规划出的路径由折线组成,路径质量差、平滑度低.
针对以上问题,以提高算法收敛速度、优化路径质量为目标,在Bi-RRT算法的基础上进行改进,保证在解决卸船机路径规划问题时算法的实时性和有效性.
2.2 改进RRT算法
对连续卸船机取料装置进行换舱路径规划时,为保证实时性,本文在Bi-RRT算法的基础上,通过以下措施进行改进,进一步提高算法的收敛速度和搜索效率.
(1)由于RRT算法是一种基于采样的路径规划算法[7],在进行采样时采样点的产生具有随机性,导致算法收敛速度较慢,生成的路径导向性较差.为提高算法的收敛速度,引入概率偏置因子ρ且ρ∈[0,1].在双向扩展随机树的生长过程中,产生一个随机值α且α∈[0,1],当α<ρ时,将目标点(起点或终点)作为采样点,使树的生长具有方向性;当α≥ρ时,在采样空间进行随机采样,保留算法对未知空间的探索能力.
(2)为了提高算法的搜索效率,结合连续卸船机的实际作业情况,对采样点的产生范围进行限制,在已知路径起点和路径终点的情况下,假设路径起点坐标(Xinit,Yinit,Zinit),路径终点坐标(Xgoal,Ygoal,Zgoal),以起点和终点作为立方体的两个对角点,在该立方体的区域内进行随机节点采样,从而减少无用节点的产生,提高算法的搜索效率[12];若在该立方体区域内由于障碍物的存在,未规划出可行路径,则在整个采样区域内进行重新搜索,智能约束采样失效.
RRT算法规划出的路径一般由许多折线组成,生成路径的质量不佳,为提高路径质量,对算法进行以下改进:
(1)引入RRT*算法渐近最优的思想,在树的扩展过程中对父节点进行重新选择和重新布线.具体方法:以二维空间为例,在产生新节点Xnew后,以Xnew为圆心、以r为半径做圆,其中,半径r要大于步长Lsegm,进而保证父节点Xnear被包含在该圆内,在该圆内的所有节点都可以作为备选父节点,遍历圆内所有节点,如图5所示,存在备选父节点1和2.比较可知,以备选父节点1作为Xnew新父节点的总路径长度要比以Xnear作为父节点的总路径长度短,所以将备选父节点1作为Xnew的新父节点,连接父节点1与Xnew,除去Xnew与Xnear的路径.在对父节点进行重新选择后,遍历圆内其他节点,考察其他节点是否会因为Xnew的父节点变化而产生其他更短路径.以节点2为例,通过节点1、Xnew到达节点2的路径长度要比通过节点1、Xnear到达节点2的路径长度短,所以除去Xnear与节点2之间的路径,连接Xnew与节点2.通过以上步骤完成重新布线操作,如图6所示.
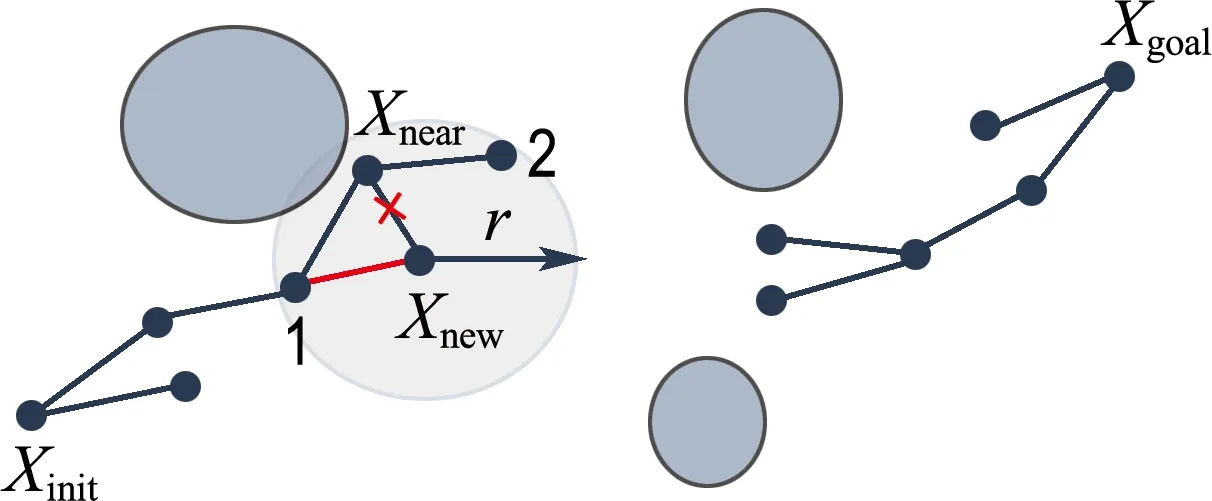
图5 父节点的重新选择

图6 重新布线操作
(2)为了进一步提高规划出的路径质量,在得到初始路径后,采用粒子群算法[13]对所规划路径进行二次优化.粒子群算法是一种群体智能优化算法,由Eberhart等在1995年提出[14-15],该算法是模拟鸟群觅食的行为,通过群体中个体之间的协作和信息共享来寻找最优解[16],主要用于解决优化问题.粒子群算法的基本思想:利用粒子来类比鸟群中的鸟,赋予每个粒子速度和位置两个属性.其中,分别采用速度和位置来描述当前粒子的移动快慢和移动方向.在求解优化问题时,每个粒子都会不断更新优化问题的最优解并经过比较得到个体历史最优位置,通过对比粒子群中所有粒子的个体极值得到全局最优位置.粒子群中的每个粒子在对速度和位置进行调整时会受当前个体历史最优位置和整个粒子群所共享的当前全局最优位置的影响,具体速度和位置的更新公式如式(1)、(2)所示.
(1)
(2)

将改进后的RRT算法与粒子群算法相结合,把改进后的RRT算法规划出的路径信息作为初始粒子,以与障碍物不发生碰撞作为约束条件,并分别以所规划路径的长度和平滑度作为适应度函数.首先采用粒子群算法对路径长度进行优化得到初始优化路径,然后再次采用粒子群算法以初始优化路径作为初始粒子对路径平滑度进行优化,此时在路径平滑度得到优化的同时,路径长度也得到了优化,优化后得到最终路径.假设路径关键点的个数为m,第j个路径关键点坐标为(xj,yj,zj),那么粒子群算法中关于路径长度和路径平滑度的适应度函数表达式分别如式(3)、(4)所示.
(3)

(xj+2-xj+1,yj+2-yj+1,zj+2-zj+1)/
(|(xj+1-xj,yj+1-yj,zj+1-zj)|×
|(xj+2-xj+1,yj+2-yj+1,zj+2-zj+1)|))
(4)
采用粒子群算法对路径进行优化的流程图如图7所示.

图7 粒子群算法优化路径流程图
通过以上措施对算法进行改进,改进后的算法流程如图8所示.

图8 改进算法流程图
2.3 算例分析
将改进后的RRT算法分别与传统RRT、Bi-RRT、RRT*算法进行比较,在三维空间(0,0,0)到(100,100,100)中随机布置球体、立方体等作为障碍物,已知起点坐标(5,5,5)和终点坐标(95,95,95),对于同一障碍物的三维环境,在RRT、Bi-RRT、RRT*、改进RRT算法中设置随机步长均为5,RRT*算法中的半径r设置为10,改进RRT算法中的概率偏置因子设置为0.5、半径r设置为10,算法中的初始种群个数为50、空间维度为3、最大迭代次数n为50,将位置参数设置为[-2,2]、速度参数设置为[-50,50],惯性因子ω设置为0.8,自我学习因子c1和群体学习因子c2均设置为1.各算法所规划出的路径如图9所示.

为了进一步说明算法的改进效果,在该环境下进行20次对比实验,每次实验所得到的路径规划时间、路径长度、采样点数、路径点数的数据如图10所示.

为了更直观地对比改进后算法的优势,现对各组实验数据进行处理,得到实验数据信息如表2所示.
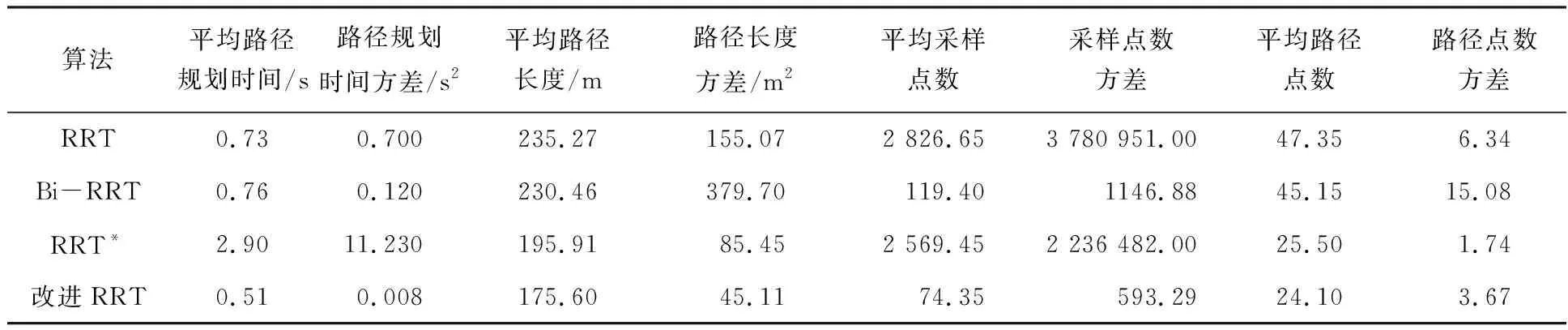
表2 实验数据信息
对比可知,改进RRT算法在完成路径规划所需时间、平均路径长度、采样点数、路径点数方面都有显著改善.其中,完成路径规划所用时间减少,搜索效率得到显著提升.改进RRT算法所规划出的平均路径长度为175.60 m,与RRT*算法规划出的路径相比,路径长度减少10.37%;改进RRT算法采样点数大幅减少,从而减少无用采样点的产生,使算法收敛速度更快,规划出的最终路径点数也减少到传统RRT、Bi-RRT算法路径点数的一半.通过对比实验可知,改进RRT算法搜索效率更高、所规划路径长度更短,能够保证算法的实时性并使路径质量得到明显改善.将该算法应用于连续卸船机的路径规划研究,能够有效提高路径规划的收敛速度、搜索效率,并能较为明显地改善路径规划质量.
3 案例分析
3.1 连续卸船机碰撞检测方法
连续卸船机通过三维激光扫描仪获取船舱以及舱内物料信息,三维激光扫描仪安装于如图11所示位置.通过顶部结构下方带云台的激光扫描仪对船舱和舱口信息进行扫描,采用取料头上方、提升筒体两侧的激光扫描仪对舱内物料进行扫描,对点云数据处理后可以得到船体和物料的坐标数据.

在进行路径规划时,船舱及舱内物料均可视为障碍物.障碍物建模的两种常用方法为包络盒法和包络球法.结合实际情况,在已知船型信息和船体坐标信息后,采用包络盒法对货船建模;在已知物料信息后,采用包络球法对物料建模.在实际作业过程中,只有连续卸船机的提升筒体部分及取料装置部分会与卸船环境中的障碍物发生碰撞,所以在此采用圆柱体对连续卸船机筒体以及取料装置进行包裹.根据连续卸船机提升筒体部分及取料装置的最大尺寸采用圆柱体对其进行等效,如图12所示.

图12 构件膨胀处理
在路径规划过程中,由于连续卸船机在进入货舱过程中依靠臂架部分的平行四边形结构使筒体部分始终垂直于地面方向,以某连续卸船机为例,其提升筒体部分的最大尺寸为5.4 m,取料装置的最大尺寸为5 m,以连续卸船机实际装置尺寸为依据,采用半径r1为2.7 m的圆柱体对取料装置的筒体部分进行包裹,采用半径r2为2.5 m的圆柱体对取料装置部分进行包裹.以某钢厂原料码头靠泊作业的智达2.3×105t散货船为例,其舱口尺寸为16 m×16 m,为避免碰撞并根据设计需求,将舱口边界尺寸及舱内物料尺寸进行膨胀处理,其原理图如图13所示.

图13 膨胀处理原理图
根据连续卸船机提升筒体尺寸将舱口部分尺寸向舱口中心方向膨胀2.7 m,防止连续卸船机提升筒体部分在换舱过程中与舱口边缘发生碰撞,经膨胀处理后,舱口部分尺寸为10.6 m×10.6 m;根据连续卸船机取料装置尺寸将舱口高度以及货舱表面高度向上膨胀2.5 m,并将料堆尺寸膨胀2.5 m,防止连续卸船机的取料装置部分在换舱过程中与船体以及舱内物料发生碰撞.在MATLAB中建立船舱模型如图14所示.

图14 船舱模型
采用包络盒法对船舱进行处理后,可将连续卸船机与船舱之间的碰撞问题转化成空间直线与立方体之间的空间交涉问题[17],假设采用改进RRT算法所规划出的路径点坐标为(x,y,z),连续卸船机取料装置的长度为l,在换舱过程中取料装置末端一直保证垂直于岸边方向向外,则连续卸船机与船舱之间的碰撞检测公式可表示为
C1={(x,y,z)|xmin (5) C2={(x,y,z)|xmin y-l (6) 式中:C1表示取料装置所在直线与船舱之间的碰撞;(xmin,ymin,zmin)、(xmax,ymax,zmax)分别表示船舱某一包络长方体的最小值坐标和最大值坐标;(x,y,z)不仅表示路径点坐标,同时也表示取料装置末端的空间坐标;s表示连续卸船机取料装置所在线段的平均采样点数;i表示采样点并且i∈[0,s].当各采样点均不与包络盒坐标重合时,则连续卸船机不会与船体发生碰撞;否则,连续卸船机与船体发生碰撞.C2表示连续卸船机提升筒体与舱口部分的碰撞;zcab表示舱口处的高度信息,当提升筒体在舱口高度处不与舱口部分发生交涉时,则不会发生碰撞,否则,连续卸船机与船体发生碰撞. 采用包络球法对舱内物料进行表示,可将连续卸船机与舱内物料之间的碰撞问题转化成求解空间直线与障碍物球体球心距离的问题.由于连续卸船机进入船舱后,取料装置部分最先与舱内物料发生碰撞,假设物料包络球半径为R,取料装置的首末空间位置坐标依次为(xs,ys,zs)、(xe,ye,ze),取料装置所在的直线L经过两点,设(x,y,z)为该直线上的点,则有 x(t)=txs+(1-t)xe, y(t)=tys+(1-t)ye, z(t)=tzs+(1-t)ze;t∈(0,1) (7) 已知,物料包络球的球心坐标为(xo,yo,zo),假设该球心到直线L上的垂直点坐标为(xc,yc,zc),则有该垂线的方向向量(xo-xcyo-yczo-zc)与取料装置所在直线L的方向向量(xe-xsye-ysze-zs)垂直,再根据垂点(xc,yc,zc)满足直线方程,便可推导得到垂直点坐标与取料装置所在的直线L之间的距离为 (8) 通过比较doc与物料包络球半径R的大小来判断连续卸船机取料装置是否与舱内物料发生碰撞,若doc>R,则取料装置未与物料发生碰撞;若doc≤R,则取料装置与物料发生碰撞. 改进RRT算法规划出的路径由许多折线段组成,存在明显拐角.为使路径更加平滑,减少对连续卸船机各个机构的冲击,采用贝塞尔曲线对路径进行平滑处理,从而得到一条平滑路径. 将改进RRT算法规划出的m+1个路径点P0、P1、…、Pm-1、Pm作为贝塞尔曲线的控制点来控制曲线形状,曲线通过路径起点P0和路径终点Pm,接近但不通过路径中间点P1到Pm-1,由m+1个控制点可以确定m阶贝塞尔曲线,其中m阶贝塞尔曲线表达式如下: (9) 在MATLAB中搭建仿真环境,如图15所示. 图15 连续卸船机仿真环境 结合连续卸船机实际作业情况,以连续卸船机需要完成从第2舱口换至第3舱口为例,已知卸船机在第2舱口内起点的世界坐标为(90,32,2),第3舱口内终点的世界坐标为(69,43,-2),采用改进RRT算法对连续卸船机换舱路径进行规划,得到的路径如图16所示.其中,黄色和绿色路径为算法执行过程中所扩展产生的随机树,黑色路径为改进RRT算法规划出的初始路径,红色路径为采用粒子群算法优化后的路径,粉色路径为采用贝塞尔曲线经过平滑处理后的最终路径. 图16 连续卸船机仿真结果 最后,对最终路径进行离散处理,通过逆运动学求解得到连续卸船机各个机构的角度、位移,为更好地验证所规划路径的可行性,建立MATLAB与CoppeliaSim联合仿真,首先将连续卸船机位姿调整于初始点所对应的位姿,然后将MATLAB所求各个机构的角度、位移信息通过通信传输给CoppeliaSim,进而使连续卸船机取料装置能够沿着规划出的路径安全运行,换舱路径如图17所示. 图17 连续卸船机换舱路径联合仿真 (1)针对Bi-RRT算法搜索效率低的问题,采用目标偏置策略并对采样点进行智能约束采样,使随机树在生长过程中具有方向性,并且减少对无用空间的搜索;为提高规划路径的质量,引入RRT*算法渐近最优思想,采用对父节点重新选择和重新布线的操作,使路径渐近最优,最后使用粒子群算法再次对路径长度以及平滑度进行优化.经实验验证,改进RRT算法具有搜索效率高、规划路径长度短的优势. (2)对障碍物进行膨胀处理并对碰撞检测方法进行研究;通过对路径进行平滑处理,从而减少连续卸船机作业时对各机构的冲击.将改进RRT算法应用于连续卸船机的换舱路径规划研究,能够有效缩短船舶停港时间,为实现连续卸船机无人化、智能化作业提供理论基础.3.2 路径平滑处理
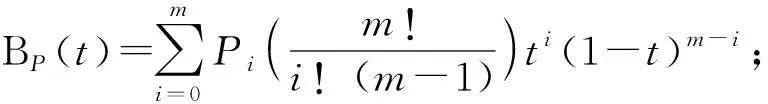
3.3 仿真实验研究



4 结 论
