联合CEEMD及AFSA优化小波阈值的心音信号去噪研究

周克良，郭春燕

（江西理工大学 电气工程与自动化学院，赣州 341000）

0 引言

心脏是维持人体生命的重要器官，负责给身体提供血液。心脏由心房和心室组成，推动血液向身体的各个器官流动，维持人体正常代谢和功能。心脏收缩舒张时产生的声音即为心音，可分为第一心音(S1)、第二心音(S2)、第三心音(S3)、第四心音(S4)，其中S1、S2正常情况下就可以听到，S3、S4仅在儿童及青少年可微弱听到[1]。心音信号在采集过程中难免会掺杂噪声，要想通过心音信号准确判断患者的身体状况，就必须要对其进行降噪处理。

目前对心音信号的降噪主要有经验模态分解(EMD)[2]，小波分析[3,4]等方法。EMD可以有效去除固有模态函数，通过对模态临界点的判断，将前面的IMF分量去除，保留高频部分IMF分量，但倘若去除的IMF分量包含有用信息，则会造成心音信号的缺失[5]。文献[6]采用了EMD和MFCC相结合的方法，但依旧无法避免选取的IMF分量造成心音信号损失。文献[7]提出总经验模态分解（ensemble empirical mode decomposition，EEMD）方法，该方法使不同比例的信号在由二元滤波器组规定的适当固有模式函数(IMF)中进行校对，并添加了白噪声的信号，以迫使集成体在筛选过程中耗尽所有可能的解。这种方法具有较好的效果，但由于添加了白噪声，容易导致噪声残留。小波分析方法是采用小波包算法对提取的心音信号进行分解，建立适当的阈值函数进行自适应处理，达到降噪的目的[3,4]；但存在阈值选择的困难，阈值过大，会造成心音信号中一些有用的信号丢失；阈值过小，会使心音中的噪音信号消除不完全。文献[8]提出基于自适应阈值函数的小波去噪，通过使用归一化香农能量来提取心音包络进行降噪；文献[9]提出一种新阈值函数，通过对阈值参数进行调整，有效的确定了各级心音的细节系数；文献[10]通过确定小波的峰值比，提出自适应小波阈值去噪。以上对小波阈值去噪都进行了一定程度的改进，但心音信号产生的失真现象以及去噪不完全仍然存在。

针对以上问题，本文提出一种联合CEEMD及AFSA优化小波阈值去噪方法。首先，采用CEEMD算法对心音信号进行分解，再用AFSA算法选取最佳阈值进行小波阈值去噪，该方法可以有效避免IMF选取不当引起的信号损失问题以及阈值选取引起的心音信号失真现象。

1 CEEMD算法原理

1.1 EMD原理

EMD可以将不同频率范围的心音信号分解成一系列的固有模态函数(IMF)单信号，每个信号都有不同的频率，IMF包含从高到低的各种频率信号[11]。基本的EMD分解原理如下：

1）原始信号为s(t)，用插值法对极小值点形成下包络hmint(t)，对极大值形成上包络hmaxt(t)，计算均值线函数I(t)；

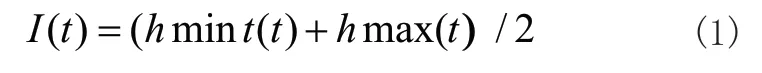
2）抽离细节信号M(t)=s(t)-I(t)；重复上诉步骤，直到M(t)满足IMF的两个条件，得到IMF分量imfi(t)；

3）用原始心音信号减去IMF作为新的待处理信号：

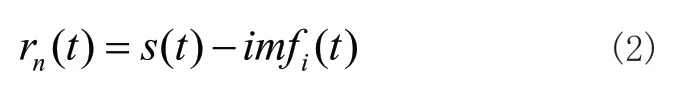
其中r(t)为残余项，s(t)为原始信号，imfi(t)为不同频率的第一个IMF分量；

4）重复上述步骤，当r(t)单调时，结束分解。

最后得到的原始信号表示为：

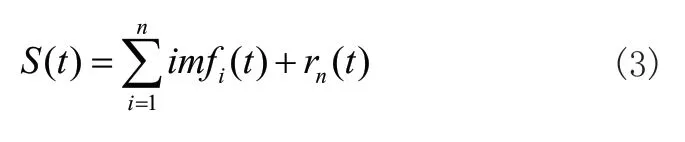
其中S(t)为分解后的信号。

1.2 EEMD原理

EEMD在原始信号中加入了高斯白噪声，根据白噪声频率分布的特征，不同尺度的信号根据特征不同分布到对应的参考尺度上，在一定程度上提高了EMD分解的精度，降低了模态混合程度[12]。具体步骤如下：

1）在原始信号中加入高斯白噪声g(t)，则信号表示为x(t)：

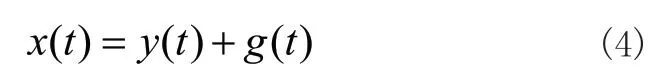
其中x(t)为添加噪声后的信号，y(t)为原始信号，g(t)为高斯白噪声信号；

2）对目标信号进行上面的EMD分解，得到rn(t)和imfi(t)；

3）重复上述步骤，直到消除加入的高斯白噪声对IMF的影响；

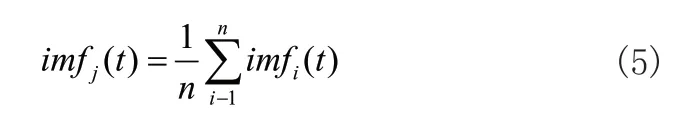
其中imfi(t)为加入噪声分解的IMF分量，imfi(t)为IMF分量的均值；

4）EEMD分解得到的信号为：

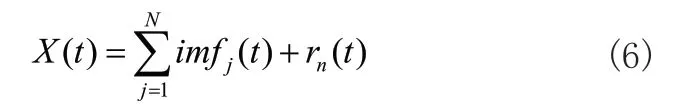
其中rn(t)为残余项，X(t)为分解后的原始信号。

1.3 CEEMD原理

EEMD在一定程度上提高了EMD分解的精度，不过完备性依旧不强，处理后的信号存在部分噪声残留现象，使得重构后的信号不完善。CEEMD是基于EMD和总体经验模式分解（General Empirical Model Decomposition,EEMD）提出的一种改进算法，可以有效解决上诉存在的问题[13]。CEEMD是在EEMD的基础上加入了两倍的高斯白噪声，使得分解具有更好的噪声消除效果，具体步骤如下：

1）在原始噪声中加入正负的高斯白噪声G(t)；

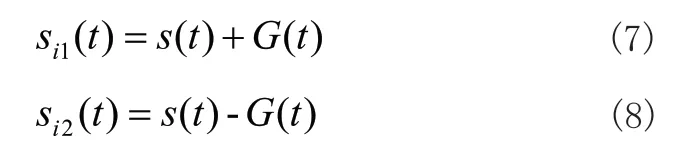
其中si1(t)和si2(t)是添加正负噪声后的信号，s(t)是原始信号，G(t)是白噪声信号；

2）对添加后的正负信号进行EMD分解，得到一系列独立的IMF；

3）重复上述步骤得到对应的IMF分量，计算所有IMF分量的平均值；

其中IMFi1和IMFi1为加入正负噪声分解的IMF分量，IMFi为IMF分量的均值；

4）CEEMD分解得到的信号为：

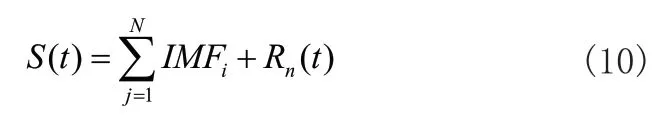
其中Rn(t)为残余项，S(t)为分解后的原始信号。

2 小波阈值去噪原理

含噪信号f(n)的数学模型一般为：

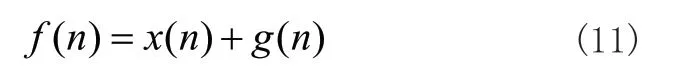
其中f(n)为含噪信号，x(n)为原始信号，g(n)为白噪声信号；

信号f(n)去噪的目的就是为了消除噪声信号g(n)，从而恢复原始信号x(n)。

小波阈值去噪的原理是：使用小波分解将采集到的信号分解到各个尺度中，再通过选择适应的阈值和阈值函数对信号进行处理，达到去噪效果[14]。小波阈值去噪基本步骤：

1）确定合适的小波基函数以及分解尺度，进行小波分解，得到个尺度分解系数；

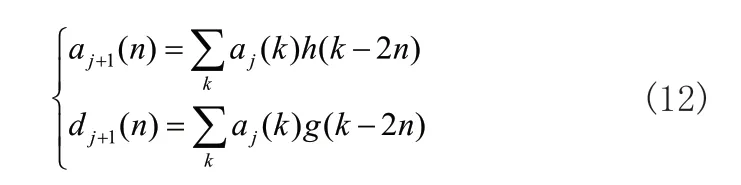
式中，aj(n)为近似系数，dj(n)为细节系数，h为低通滤波器系数，g为高通滤波器系数，j为分解层数，n为采样点数目，k=1,2,3,...,n-1。

2）通过选择合适的阈值和阈值函数对小波分解系数进行阈值处理，得到估计小波系数；阈值和阈值函数的选取是去噪性能好坏的关键，阈值函数的选取可以使得不连续的信号变得连续。传统阈值函数包括硬、软阈值函数，其表达式如式(13)所示：

硬阈值函数表达式为：

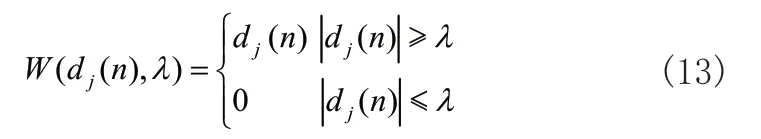
软阈值函数表达式为：

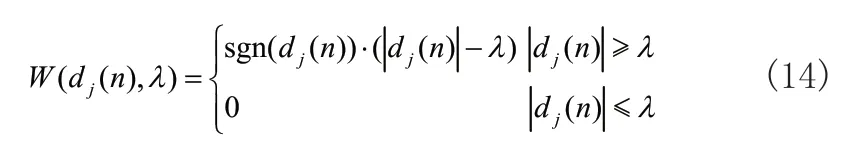
由上述式子可以看出传统的阈值函数都存在一定的缺陷，硬阈值函数不连续容易将有用信息滤除，从而导致信号失真；软阈值函数相对于硬阈值更加平滑，但若分解的小波系数绝对值偏大，则容易使其减小造成高频点信号偏差较大。

为了弥补传统软硬阈值函数的不足，本文提出一种改进的阈值函数：

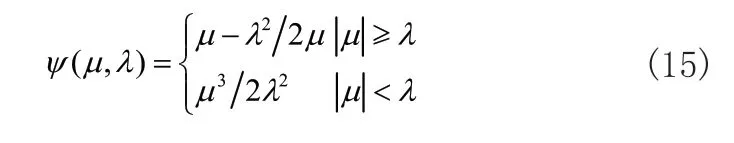
其一阶、二阶导数如下：

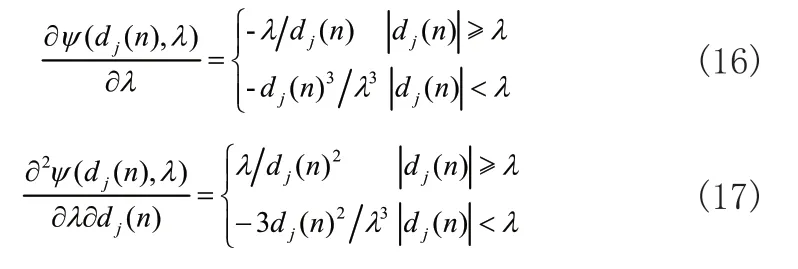
阈值选取不当将会使信号去噪不完全甚至出现失真现象，小波阈值的选择有很多，根据文献[15]进行梯度迭代优化：第n+1次迭代的阈值等于前一次迭代的阈值减去均方误差，即：

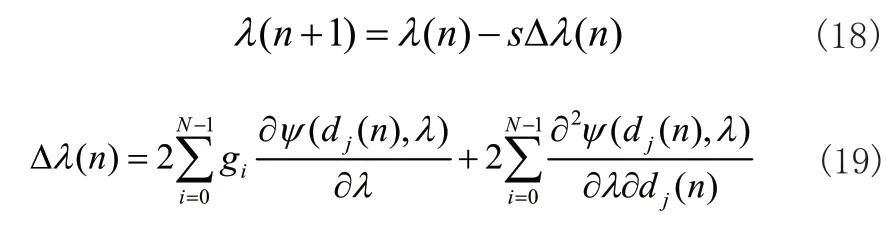
式中，s为步长，Δλ(n)为函数梯度值，gj=Ψ(dj(n),λ)-dj(n)。

3）利用估计小波系数进行信号重构，得到重构信号y(n)，即为去噪后信号。重构公式为：

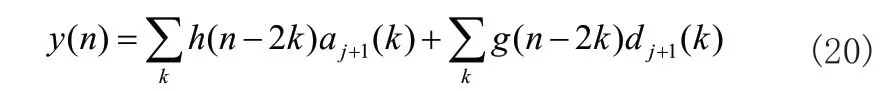
根据式(20)得到的即为去噪后的心音信号。

3 基于人工鱼群算法的小波阈值去噪

3.1 人工鱼群算法原理

人工鱼群算法(Artificial Fish－Swarm Algorithm，AFSA)是李晓磊等人于2002年提出的一类基于动物行为的群体智能优化算法[16]。主要是通过模拟鱼类的觅食、聚群、追尾、随机等行为，通过鱼群中各个体的局部寻优，从而达到全局寻优的目的。主要行为描述如下：

1）觅食行为

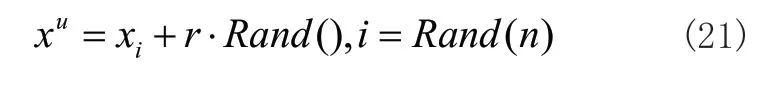
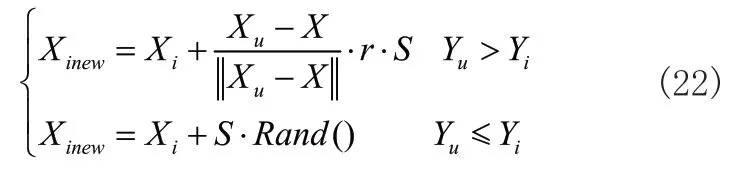
式(22)中，r表示视觉半径，x表示人工鱼当前位置，S表示步长，Y表示食物浓度。当人工鱼在视线半径r内发现食物浓度更高的位置Xu时，人工鱼将向Xu移动一步。若新位置的食物浓度低于当前位置浓度，人工鱼将随机移动步长。

2）聚群行为

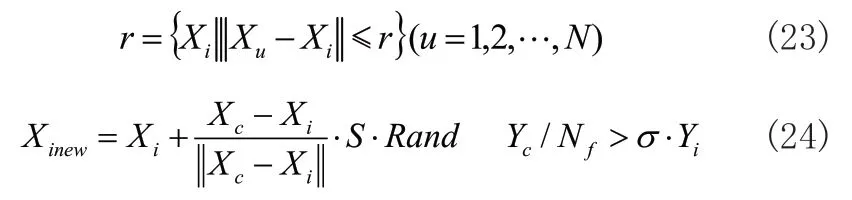
式中，σ为拥挤度因子，Xc为中心位置。在视觉范围r内，找到食物浓度高的鱼群，并计算中心位置Xc，若拥挤度因子σ正确，则人工鱼向新位置移动一步；否则执行觅食行为。

3）追尾行为

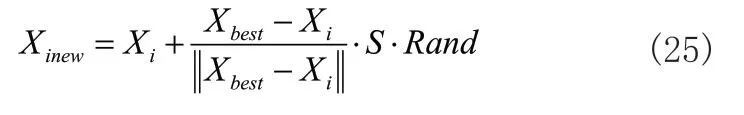
在附近的鱼群找到食物浓度较高的个体后，若拥挤度因子σ满足，则人工鱼向该位置移动。

3.2 人工鱼群优化小波阈值算法

阈值的选取是小波阈值去噪的关键之一，阈值选择过小，心音中的噪声信号消除不完全；阈值过大，容易导致有用信号消除，使得心音信号失真。文献[15]提出的梯度下降法对阈值进行寻优，容易出现收敛速度慢以及计算时间长等问题，文献[17]提出的遗传算法进行寻优，容易出现过早收敛，寻优效率低等问题。为此，本文提出搜索能力强，搜索速度快具有全局寻优能力的人工鱼群算法(Artificial Fish－Swarm Algorithm，AFSA)对式(18)(19)进行迭代寻优，找到最佳的阈值。具体思路如下：

1）相关参数初始化。即设定鱼群总数N、每条人工鱼初始位置λ(n)以及视野范围Visual、移动步长S、拥挤度因子σ、最大迭代次数MAXGEN；

2）计算初始个体的适应度值Δλ(n)，当Δλ(n)最小时，Δλ(n)达到最优，取最优人工鱼的值赋予给公告板；

3）根据式(22)、式(24)、式(25)更新鱼群位置λ(n)，并且与公告板进行比较，取两者的最优值赋予公告板；

4）当公告板上的最优值达到满意值或者达到最大迭代次数时迭代结束，输出最优阈值λbest，否则转至步骤2：

5）由式(15)再根据得到的最优阈值进行小波阈值去噪。

其中AFSA算法的参数设定如下：鱼群总数N=50，最大迭代次数MAXGEN=200，视野范围Visual=12，移动步长S=0.2，拥挤度因子σ=0.5。人工鱼群算法优化小波阈值流程图如图1所示。

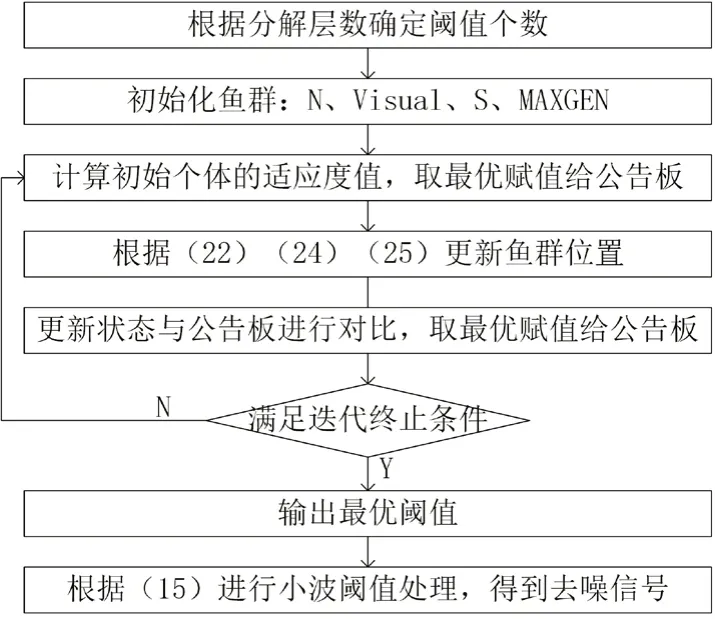
图1 人工鱼群算法优化小波阈值去噪流程图

4 联合CEEMD及AFSA优化小波阈值去噪算法

简单的运用CEEMD去噪容易造成有效信息的丢失，单独的小波阈值去噪不能较好的体现原始信号的自适应性且去噪不完全。为此提出CEEMD及AFSA优化小波阈值联合去噪算法对心音信号进行去噪。联合算法既可以结合CEEMD分解去噪的优势，又可以克服小波阈值去噪的不足，能有效去除噪声，保存心音信号中的有效信号。图2所示为联合CEEMD及AFSA优化小波阈值去噪算法过程，具体实现步骤如下：

图2 联合CEEMD及AFSA优化小波阈值去噪算法流程图

1）对信号进行CEEMD分解，得到若干个IMF分量；

2）采用AFSA算法对改进小波阈值去噪方法选定一个最优阈值；

3）选择高频IMF分量采用(2)选定的阈值进行小波阈值去噪；

4）将去噪后的IMF分量与其他IMF分量进行信号重构，得到去噪后的信号。

5 实验结果与分析

为了分析联合CEEMD及AFSA优化小波阈值去噪算法的有效性，本文用赣南医学院第一附属医院以及丁香园采集的数据进行试验。其采样频率为11025Hz，量化值为16bit，采集的心音信号以.wav格式保存，再用matlab2019进行仿真，如图3所示为采集到的二尖瓣关闭不全信号。

将采集的心音信号进行CEEMD分解后得到12个IMF分量如图4所示，由图3可知二尖瓣关闭不全信号频率主要集中在0～5kHz之间，而IMF1分量频率主要集中在5kHz以上，且幅值较低，主要是一些干扰的背景噪声，故将其忽略。对分解的高频信号IMF2、IMF3和IMF4分量进行小波阈值去噪处理。

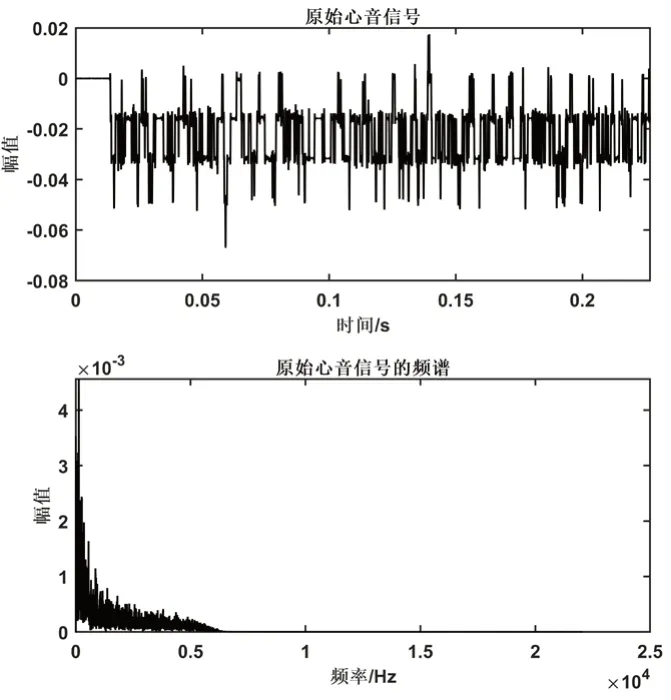
图3 原始心音信号及其频谱图

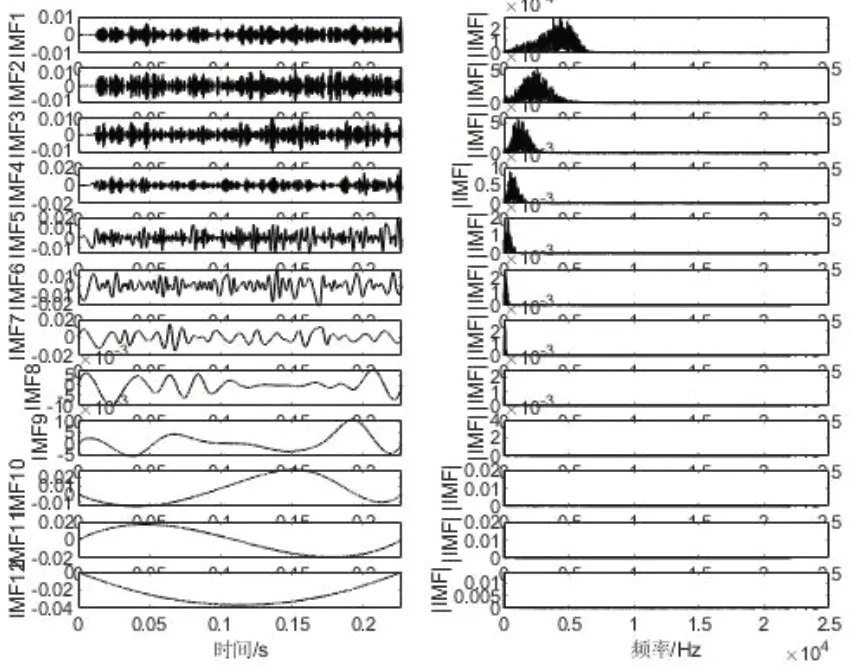
图4 CEEMD分解的各IMF分量及其频谱图

本文选取对心音信号有良好分析性能的db6作为小波基函数对IMF分量进行5层分解如图5所示，然后采用AFSA对改进的阈值函数进行阈值寻优去噪，最后将去噪后的分量与其他IMF分量进行重构，得到去噪后的信号如图6所示。

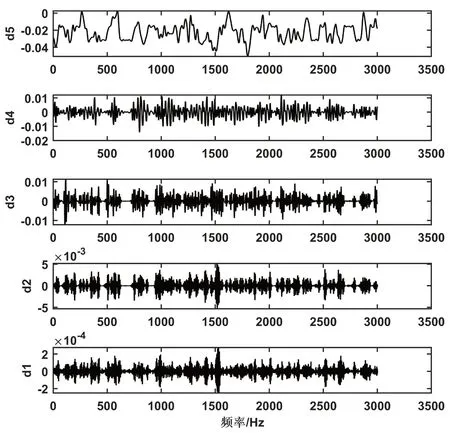
图5 小波5层分解图

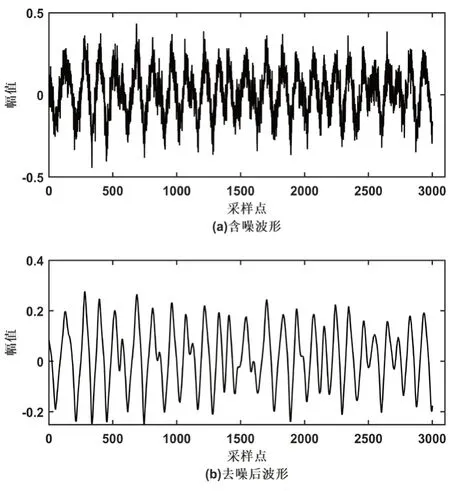
图6 联合算法去噪图

为了体现联合CEEMD及AFSA优化小波阈值去噪算法的优越性，将含噪心音信号分别用CEEMD算法、小波阈值算法以及联合CEEMD及AFSA优化小波阈值去噪算法进行去噪，得到的去噪对比图如图7所示，从图中可以明显的看出CEEMD去噪算法造成了信号的大量丢失，小波阈值去噪相对CEEMD去噪效果较好，但去噪不完全，而联合CEEMD及AFSA优化小波阈值去噪弥补了前面两个算法的不足，去噪效果更佳。

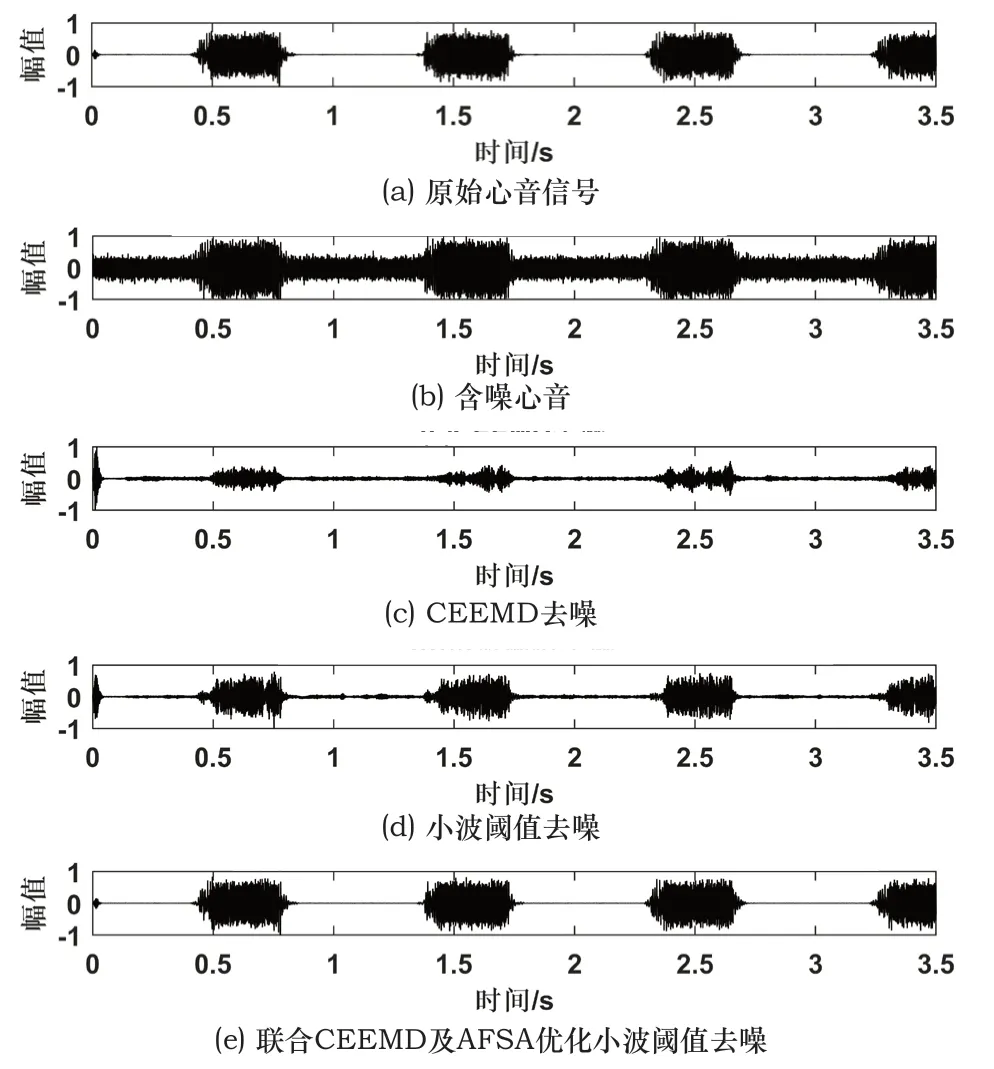
图7 三种去噪方法对比图

信噪比是评估去噪性能最常用的指标，信噪比(SNR)越高，说明去噪效果越好。从表1中的数据可以看出，联合CEEMD及AFSA优化小波阈值去噪相比于CEEMD去噪方法，信噪比提高了25.98%，均方根误差降低了34.68%；相比于小波阈值去噪方法，信噪比提高了22.65%，均方根误差降低了31.52%。

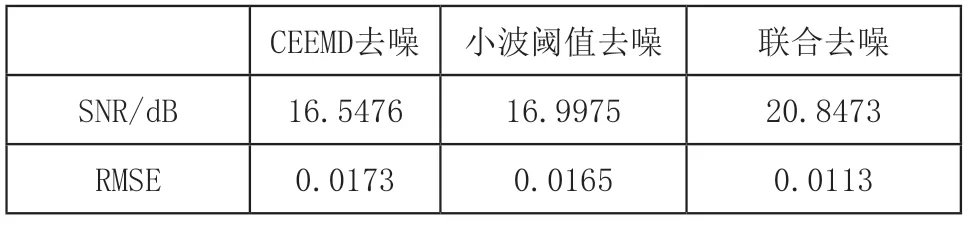
表1 三种方法去噪结果对比

综合以上不同的对比形式可得，联合CEEMD及AFSA优化小波阈值去噪方法效果优于CEEMD去噪和小波阈值去噪，且较好的展现了心音信号的特征，心音信号去噪效果得到了较大的改善。

6 结语

由于心音信号具有非平稳特性，单独的CEEMD去噪和小波阈值去噪都难以使信号在不失真的情况下达到较好的去噪效果。本文不仅将两种算法进行了结合，而且对小波的阈值函数进行了改进，改进的阈值函数克服了传统的软、硬阈值函数不连续和偏差大的问题，并且采用了搜索能力强，搜索速度快具有全局搜索能力的人工鱼群算法对阈值进行优化，解决了阈值选取不当造成的信号失真问题。与CEEMD去噪和小波阈值去噪进行对比可以看出，联合CEEMD及AFSA优化小波阈值去噪取得的去噪效果最好，同时减少了信号的失真。