基于坠落机制的混沌麻雀算法AGV路径规划*
2023-02-03李一铭王跟成
李一铭 王跟成
(①西藏民族大学信息工程学院,陕西 咸阳 712082;②西藏自治区光信息处理与可视化技术重点实验室,陕西 咸阳 712082;③西藏网络空间治理研究基地,陕西 咸阳 712082)
自动导引运输车(AGV)的路径规划问题是在确保AGV安全的前提下,规划出一条效率最高且能够成功到达目标位置的路径。
传统的AGV路径规划算法有A*算法[1]、人工视场算法[2]等。随着智能仿生学算法的发展和应用,越来越多的学者将蚁群算法(AOC)[3]、麻雀搜索算法(SSA)[4]等应用于AGV路径规划。其中,麻雀搜索算法是一种启发式的随机搜索算法,具有优秀的寻优能力和鲁棒性强的优点,但它和其他启发式算法一样存在初试种群多样性较弱、收敛速度慢以及最短路径平滑性不足的缺点。针对以上问题,宋立业[5]等通过Tent映射改进麻雀算法提高了算法的种群多样性;魏晓鸽[6]等使用精英反向学习策略和动态权重系数的正弦余弦优化算法改进麻雀算法,提高了算法在的路径寻优能力;齐鹏飞[7]等通过改进灰狼优化(GWO)算法,有效避免了GWO算法目的地无法抵达的问题,并且提高了GWO算法的寻优能力。以上改进方法在不同程度上提高了算法的寻优能力,但仍然存在收敛速度慢、寻优路径拐点处平滑性较差的缺点。
基于以上学者的研究,本文提出了基于坠落机制的混沌麻雀优化算法(SSA-CD)来解决AGV路径规划算法。该算法引入变尺度混沌初始化种群提高种群多样性;其次,引入动态黄金正弦策略提高算法发现者位置更新方式;提出了一种坠落机制;最后,通过埃尔米特插值平滑策略,进一步优化最优解,获得更短更平滑的路径。从而提高了AGV路径规划的平滑性和性能,并将算法进行仿真实验。
1 基于坠落机制的混沌麻雀算法(SSA-CD)
1.1 初始化操作
出于模拟需要,通过栅格法[3]在二维平面上构建解空间,搭建20 m×20 m栅格地图环境,将障碍物定义为黑色不可行区域,白色栅格为可行区域作为路径的生成节点,AGV在栅格内共有8个行驶方向,栅格地图环境如图1所示。

图1 栅格地图环境
1.2 麻雀搜索算法
麻雀搜索算法是一种受麻雀种群进食行为启发提出的一种仿生优化算法。
发现者具有较好的全局搜索能力能够带领种群向食物源移动,一般占种群规模的20%。发现者位置更新公式为

式中:t为当前迭代次数,Tmax表示最大迭代次数;xi,j为第i只麻雀在第j维度上的位置信息;a为一个[0,1]之间的随机数。R2和ST分别表示预警值和安全值。当R2小于ST时表明发现者处在安全区域,可以进行广泛的全局搜索,当R2大于ST时表明发现者察觉出危险,并向其他麻雀发出报警信息,带领种群逃出危险区域;Q为服从正态分布的随机数;L为1×d的全1矩阵。
麻雀搜索算法在每次迭代过程中,选择种群位置中位置最优的作为发现者,剩余的麻雀作为加入者,加入者的位置更新公式为
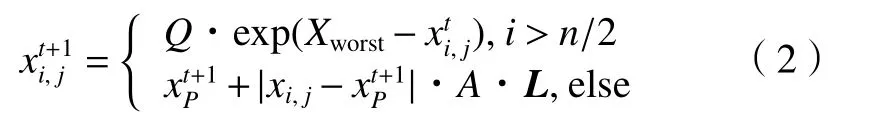
式中:Xp表示当前迭代中最优适应度的发现者位置,Xworst表示为全局适应度最差的麻雀个体位置。L为一个随机赋值为1或-1的1×d矩阵,A+=AT(AAT)-1。n为种群的数量,当i>n/2是,表示加入者处于饥饿状态需要飞行到其他位置寻找食物,当i 式中:xb表示当前迭代全局最优适应度位置;β是步长控制参数,是一个符合正态分布的随机数;K为[-1,1]的随机数;z是最小的常数,用以避免分母出现0的情况。fi和fw分表表示最优和最差的适应度。当麻雀处于最优位置则逃离到以自身附近的位置。当麻雀处于较差位置时,则将逃出到当前最优位置附近。 为了增强算法初始化种群的多样性,本文引入Sinusoidal混沌映射完成麻雀种群初始化,混沌映射公式为 其中:本文取a=2.3、x1=0.7。迭代次数为1 000次的混沌状态种群初始化如图2所示。由图2可知,使用Sinusoidal混沌映射初始化的种群分布更加均匀,能够获得比随机初始化更加稳定分布的初始化解。 图2 Sinusoidal混沌映射图 在搜索空间减小的问题上,混沌映射表现较好。当搜索空间较大时,混沌映射可能存在失效的情况,因此在混沌映射公式中加入尺度变换来增强其在较大搜索空间上的表现性能。引入尺度变换的混沌映射公式为 其中:t为当前迭代次数,Tmax为最大迭代次数。当最优值在迭代10次还为发生变化时,可以认定为算法进入搜索停滞状态。此时需要将种群再次通过混沌映射进行扰动,增加种群的随机性,使算法跳出搜索停滞状态。 发现者的搜索范围较小的问题导致SSA算法存在易于陷入局部最优和搜索停滞的缺陷。式(1)中的exp(-i/(αTmax))起到决定发现者勘探能力的作用,令p=exp(-i/(αTmax)),则其变化曲线如图3所示。根据i值的不同,p的值总是落在[0.9,1],从而导致发现者的位置搜索范围较小,并且在迭代过程中种群不断的趋近于0,由于发现者起着引领种群的特点,因此将导致整个种群在不断的趋向于非原点。当R2≥ST时,发现者所使用的正态随机数的扰动策略效果有效。为了增强麻雀搜索算法的全局搜索能力,本文通过引入动态调整的黄金正弦[8]策略来改进发现者全局搜索公式,增强发现者全局搜索能力和全局寻优速度。改进后的发现者更新公式为 图3 参数p的数值分布 其中:xP为当前迭代中最优适应度个体位置,r1和r2分别为取值 [0,2π]和 [0,π]的随机数,c1和c2表示黄金分割系数,c1=a(1-g)+bg、c2=ag+b(1-g)、黄金分割率g=0.618,c1和c2缩小了搜索空间,在迭代过程当中可以引导麻雀个体向全局最优位置移动。 受文献[6]中引入惯性权重思想的启发,为了更好的平衡算法全局搜索和局部寻优能力,改善算法在迭代后期陷入搜索停滞状态的问题,在黄金正弦更新公式中引入非线性自适应权重w,表达式为 非线性惯性权重保证算法在迭代初期全局探索范围更大且更快的递减速度有利于减少算法全局探索的迭代次数。随着迭代次数的增多,探索范围逐渐收敛切收敛速度减缓,更有利于算法进行局部挖掘,解决算法后期因为范围减小带来的搜索停滞问题。加入非线性自适应权重的发现者位置更新公式为 在标准SSA算法中,发现者位置更新的正态分布随机数扰动的效果随着迭代的增加效果有限,为了增加SSA算法的随机性, 本文提出一种坠落机制,即麻雀在飞行和觅食的过程中有一定概率发生坠落或者被其他大型鸟类捕食的现象。为了确保经过坠落后的种群数量不变,我们通过麻雀的位置和麻雀下降的步长来建立坠落机制模型,其具体模型为 其中:r3、r4和r5为取值区间(0,1)的随机数,xstep为麻雀的坠落步长,其具体定义如下。 其中:ub和lb为第i维度的取值上界和下界,n为问题的维度,C2为步长因子,可以看出步长因子受迭代次数和最大迭代次数的边界影响。麻雀坠落的概率Wf从迭代前期的0.1逐渐减少到0.05,表明在优化过程当中,随着麻雀靠近最优值解危险逐渐降低。 SSA算法生成的路径仍然不够平滑,部分路径中还存在尖锐拐点。受文献[9]中通过B样条曲线平滑路径的思想启发,在改进SSA算法的基础上引入三次埃尔米特插值多项式。埃尔米特插值和贝塞尔曲线[10]相比,具有能够克服贝塞尔曲线存在的局 部性质缺点的能 力 。 设在节点a≤x0<x1< ···<xn≤b上满足条件yi=f(xi),mi=f(xi)(i=0,1,···,n),要求插值多项式H(x)满足条件 因插值节点一共存在n+1个,当给出2n+1个条件的时候,可以唯一确定一个次数不超过2n+1的多项式H2n+1(x)=H(x),其表达式为 由基函数构建埃尔米特插值多项式需要先求出插值的基函数 αi(x), βi(x)(i=0,1,···,n),因而共得到2n+2个基函数,每个基函数为一个2n+1次的多项式,并且需要满足 结合以上条件生成的埃尔米特插值项式的公式为 其中,三次埃尔米特插值的数学描述如下。 埃尔米特插值通过在区间内生成一系列的中间插值节点,能够生成一条平滑的曲线。通过将三次埃尔米特插值曲线引入到VGA的全局路径规划当中,可以使得VGA的路径移动更加符合动力学原理。 改进后的算法流程如图4所示。 图4 算法整体流程图 为了验证算法在低密度环境下,算法对AGV路径寻优的可行性和有效性,本实验选取环境大小为20 m×20 m的二维环境,AGV所处的起始位置为(0,0),终点位置为(20,20)。实验设置种群规模为50,最大迭代次数为200次,单位栅格的边长为1 m。分别采用CAO算法、CAO-GA算法[11]、SSA算法、混沌麻雀(SSA-C)[12]算法和SSA-CD算法进行路径规划。其中ACO算法的信息素重要程度因子a=1、b=5、q=2 000、信息素的挥发因子p=0.7;SSA算法的参数设置为PD=70%、R2=0.8、SD=20%。各算法的最优路径对比如图5所示,记录各算法的迭代收敛曲线和最优路径信息如图6和表1所示。 5种算法的迭代收敛过程如图6所示,由图可以看出,SSA-CD算法的收敛精度优于其他对比算法。其中ACO-GA算法和SSA算法在迭代过程中陷入搜索停滞状态,全局搜索能力较差。在迭代到40次左右时SSA-CD算法完成收敛,优于其他对比算法。并且通过对比收敛曲线拐点数量可知,ACO算法收敛过程中拐点数目较多,SSA-CD算法收敛迭代过程收敛速度较快、拐点数目少,全局搜索和局部探索阶段较为平衡,能够更好地跳出局部最优解。 图6 5种算法迭代曲线对比 从图5和表1中可以看出,SSA算法的最优路径长度为34.34 m,SSA-C的路径长度为28.22 m,相较于SSA算法路径减少了17.82%;SSA-CD算法对路径进行平滑优化后的路径长度为27.20 m,相较于SSA-C算法路径长度缩短了3.61%,表明了本文所提出的改进方法对于路径长度缩短的有效性和可行性,能够增强算法的全局收敛能力和局部探索能力,使算法具有更好的探索精度。ACO-GA算法的平均路径长度为32.62 m,优于ACO算法的路径长度34.34 m,算法拐点数目较少,但是算法运行时间较长,不利于AGV路径规划对实时性的要求;ACO和SSA算法的迭代运行时间较为接近分别为12.45 s和11.81 s,迭代次数为63和65次,而SSACD算法的运行时间为8.95 s,迭代次数为40次,表明本文改进方法能够增强初试种群的多样性,并且能够缩短算法的全局探索能力,提高算法局部收敛精度,进一步表明本文算法改进的有效性和可行性。从整体上来看路径寻优能力上SSA-CD算法>SSA-C算法>ACO-GA算法>ACO算法。综上所述,本文算法相较于ACO算法能够减少20.7%的路径长度,优于对比算法。 表1 4种算法数据结果 图5 5种算法仿真结果 为了进一步证明算法的有效性和鲁棒性。设置规模为40 m×40 m的正方形区域,栅格的大小为40×40,选取传统的A*算法、SSA算法、SSA-C和SSA-CD算法进行AGV路径规划。通过增加障碍物的数量和密度来验证算法的鲁棒性,实验结果如图7和表2所示。 表2 4种算法数据结果 图7 4种种算法仿真结果 由图7和表2可知,本文算法的路径长度最短为57.92 m,优于其他算法。在算法寻优过程中A*算法陷入死区,路径规划失败,表明本文改进的算法相较于传统A*算法具有更好的鲁棒性。未经过平滑处理的SSA-C算法的规划路径长度为60.42 m,经过平滑处理后的SSA-CD算法比SSA-C算法路径减少了4.13%,由此可以看出,不管在低密度和高密度环境下,三次埃尔米特插值平滑处理都可以减少路径并且减少路径的拐点数,提升了路径规划的能力。与传统SSA算法相比,本文算法的规划路径长度减少了8.45 m,进一步证明了本文改进算法的有效性、鲁棒性和可行性,能够完成复杂环境下AGV路径规划任务。 针对高密度复杂环境下的自动导引运输车的路径规划问题,本算法通过融合混沌麻雀算法和三次埃尔米特插值解决AGV路径规划问题,并且通过变尺度混沌策略提高了麻雀算法的种群多样性、收敛速度和寻优精度,引入动态黄金正弦策略增强算法种群位置更新方式多样性,然后提出了一种坠落机制,增强算法的随机性,并且将三次埃尔米特插值方法引入到生成路径的平滑处理中。最终通过实验表明本文算法有效提高了自动导引运输车的路径规划质量,能够在保证生成路径效率最优的同时减少拐点数量。今后还需深入研究不同环境对自动导引运输车路径规划的影响,进一步提高算法的应用场景并将算法应用于实际场景中。
1.3 变尺度混沌策略



1.4 动态黄金正弦策略




1.5 坠落机制


1.6 三次埃尔米特插值方法





1.7 算法流程

2 实验结果与分析
2.1 简单环境下对比试验



2.2 复杂环境下对比试验


3 结语
