基于M−K理论的NbTiAl合金高温成形极限曲线预测

孟宪国，闫静锴，雒亚涛，周兵营，崔学习，吴向东

轻合金成形

基于M−K理论的NbTiAl合金高温成形极限曲线预测

孟宪国1，闫静锴2，雒亚涛1，周兵营2，崔学习2，吴向东2

（1.西安航天发动机有限公司，西安 710100；2.北京航空航天大学 机械工程及自动化学院，北京 100191）

NbTiAl合金在常温下的塑性较差，针对300 ℃时NbTiAl合金的成形性能进行研究，探究其在高温环境下的力学性能和成形极限，分析理论预测成形极限的可行性，为进一步研究铌合金性能和扩展其工程应用提供理论参考。采用高温单拉和高温成形极限试验，获得了NbTiAl板材在300 ℃的应力应变曲线及成形极限曲线，使用Swift硬化模型针对塑性变形段进行拟合，并采用M−K失稳理论，结合相应的材料本构模型，对NbTiAl合金在高温环境下的成形极限进行了理论预测，并与实验数据进行了对比。NbTiAl合金在300 ℃时的塑性应变阶段仍然具有加工硬化效应，在初始厚度不均度0为0.998时，得到的理论曲线与试验点在左侧拉−压区符合得较好，但对右侧拉−拉区的理论预测与试验结果相差较大。NbTiAl合金在300 ℃时具有较好的成形性，采用合适的不均匀度系数，利用M−K理论可以较好地预测NbTiAl合金高温成形极限曲线左侧拉−压区的极限应变，但对右侧拉−拉区域极限应变的预测结果误差较大。

NbTiAl铌合金；M−K模型；高温成形极限；塑性失稳；理论预测；本构方程

随着航空航天技术的迅速发展，各国将研究的焦点汇聚在新型高温材料上，传统的镍基高温合金由于其使用温度极限不超过1 200 ℃，因而无法满足下一代高性能发动机的要求，近30 a各国深入研究了铝系金属间化合物，但其最高使用温度同样低于1 200 ℃。硅基高温陶瓷材料的使用温度虽然可以满足要求（可以达到1 600 ℃），但其使用时的可靠性较差，依然不能作为航空结构材料的备选。由此，各国将目光转移到了价格较为昂贵但非常有发展前景的铌合金上[1]。

作为未来发动机零件的候选材料之一，NbTiAl合金具有低密度、高温比强度高、高塑性、高韧性、优秀的抗腐蚀性能与冷热成形性能等优点[2]，通过加工成形状复杂的零件，可以应用于火箭发动机、卫星姿控发动机和超髙音速飞机等领域[3]，是非常具有发展潜力的超高温结构材料。在发动机上，铌合金零部件主要采用板材毛坯通过旋压工艺进行成形，在成形过程中不可避免会出现破裂和回弹等缺陷。板材的成形极限能够反映出在成形过程中板材发生塑性失稳前能够达到的最大变形程度[4]，是评价板材成形性能的综合指标。成形极限图（Forming Limit Diagrams，FLD）是众多评价板材成形性能方法中最有效、最直观、最广泛的方法，是评估板材成形性和解决板材冲压问题非常有效的工具[5]。Park[6]比较了常规成形和增量成形中板料的成形极限曲线，发现成形极限曲线无法描述增量成形应用中的失效，即应变超过常规成形极限曲线而没有发生失效。Jain等[7]通过试验确定AA6111−T4板材在颈缩和断裂处的成形极限曲线。Arrieux[8]根据试验中板料失稳时的应力状态和应变路径无关的现象，首次提出了成形极限应力图（forming limit stress diagram，FLSD）的概念，并基于Nakazima试验和Mises屈服准则对成形极限应力图进行测定。获得成形极限曲线（Forming Limit Curves，FLC）的方法主要是实验与理论模型预测，试验获得FLC的成本很高。目前，有关NbTiAl合金成形极限的试验研究还未见报道，针对NbTiAl合金的成形极限开展试验和理论研究具有非常重要的实际工程应用价值和理论意义[9]。

1 NbTiAl合金板材高温成形性能试验

1.1 高温单向拉伸试验

材料为轻质铌钛铝合金板材（牌号为NbTiAl），其化学成分见表1，厚度为1 mm。试验采用配备高温环境箱的Zwick Z010材料试验机，应变采用视频引伸计测量，试样尺寸（mm）和试验环境见图1。

研究目的是初步分析铌合金的高温准静态变形行为，暂不考虑应变速率影响，故选择变形条件为温度300 ℃、应变速率0.001/s，最终获得材料的真实应力−真实应变曲线见图2。

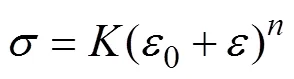
表1 NbTiAl合金板材化学成分

Tab.1 Chemical composition of NbTiAl sheet wt.%

图1 单拉试样尺寸及试验设备

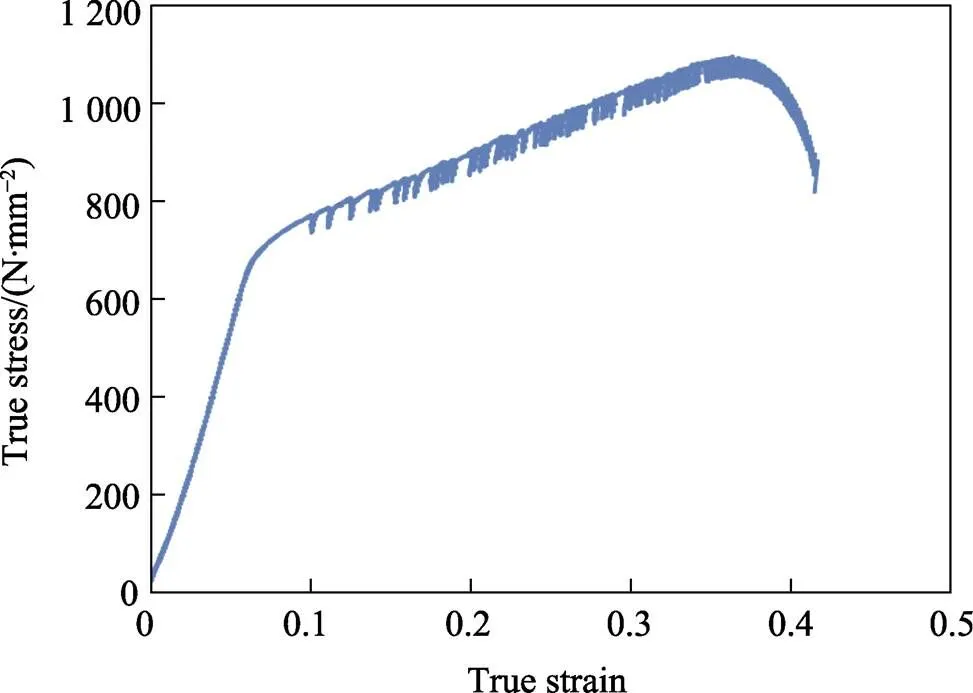
图2 NbTiAl合金材料真实应力−真实应变曲线

1.2 高温成形极限试验

高温成形极限试验是采用刚性凸模对试样进行胀形的方法。根据试验装置特点和实验原理，为了防止窄条矩形试样在拉深筋处开裂，将试样确定为中部较窄并向两端圆弧过渡的尺寸形状，试样为厚度规格1.0 mm的铌合金钢板，测试温度为300 ℃，其尺寸见图3（单位mm）。试样用激光切割加工并对边缘进行打磨。

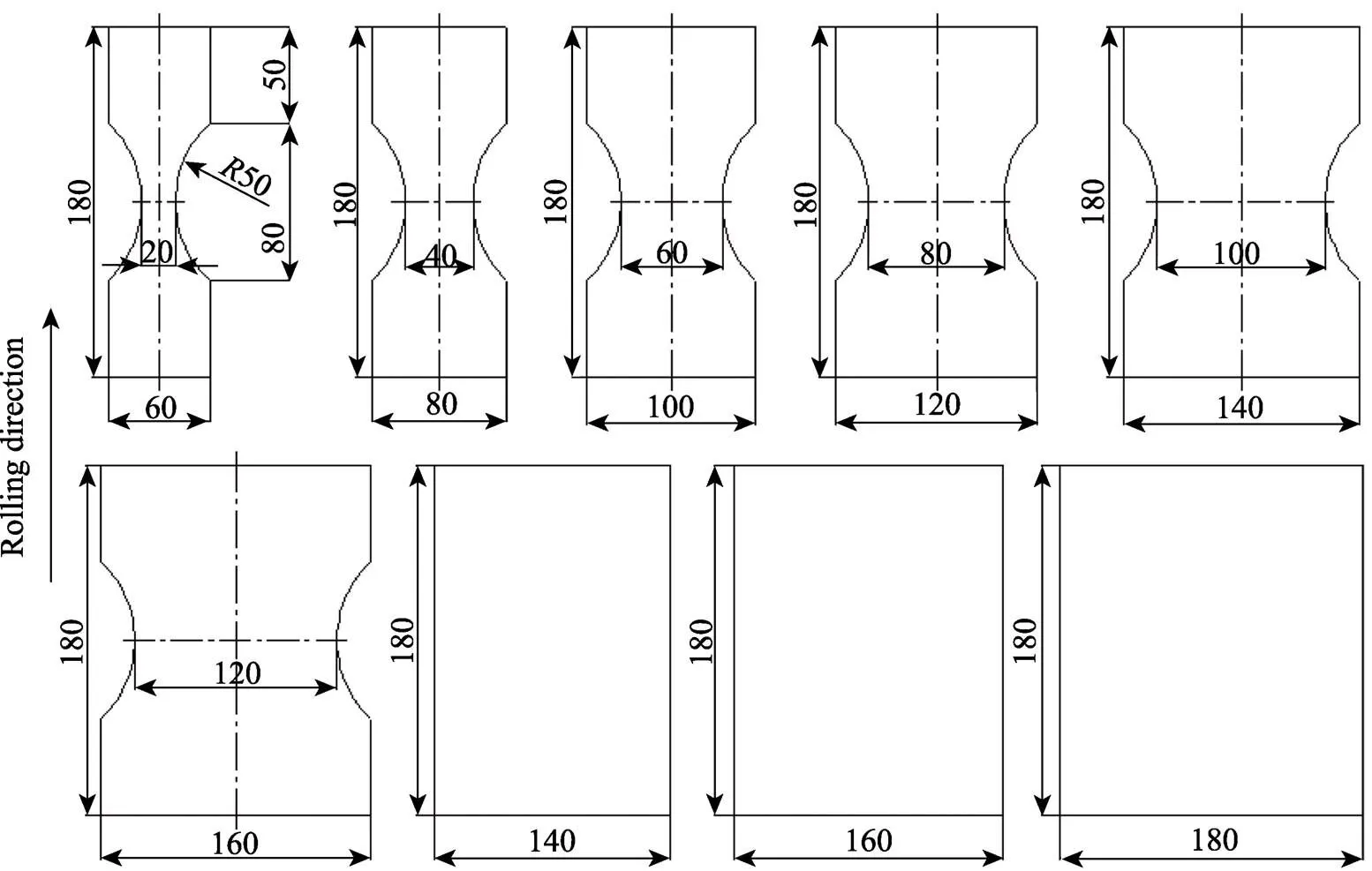
图3 FLD试验试件及几何尺寸

试验在中科院沈阳金属所进行，设备为北京航空航天大学研制的热环境通用板材成形试验机（图4），采用真空炉电阻加热方式，模具和试样随炉加热，试验结束后采用风冷进行冷却。

成形极限试验原理见图5a，在试样表面印制网格，将高温润滑剂涂抹在试样和凸模接触部位，放置好模具和试样后开始抽真空加热，加热到300 ℃并保温0.5 h，以保证板材温度均匀。试验过程采用载荷控制，当试样发生破裂导致凸模载荷下降时试验终止。获得的材料FLC曲线见图5b。

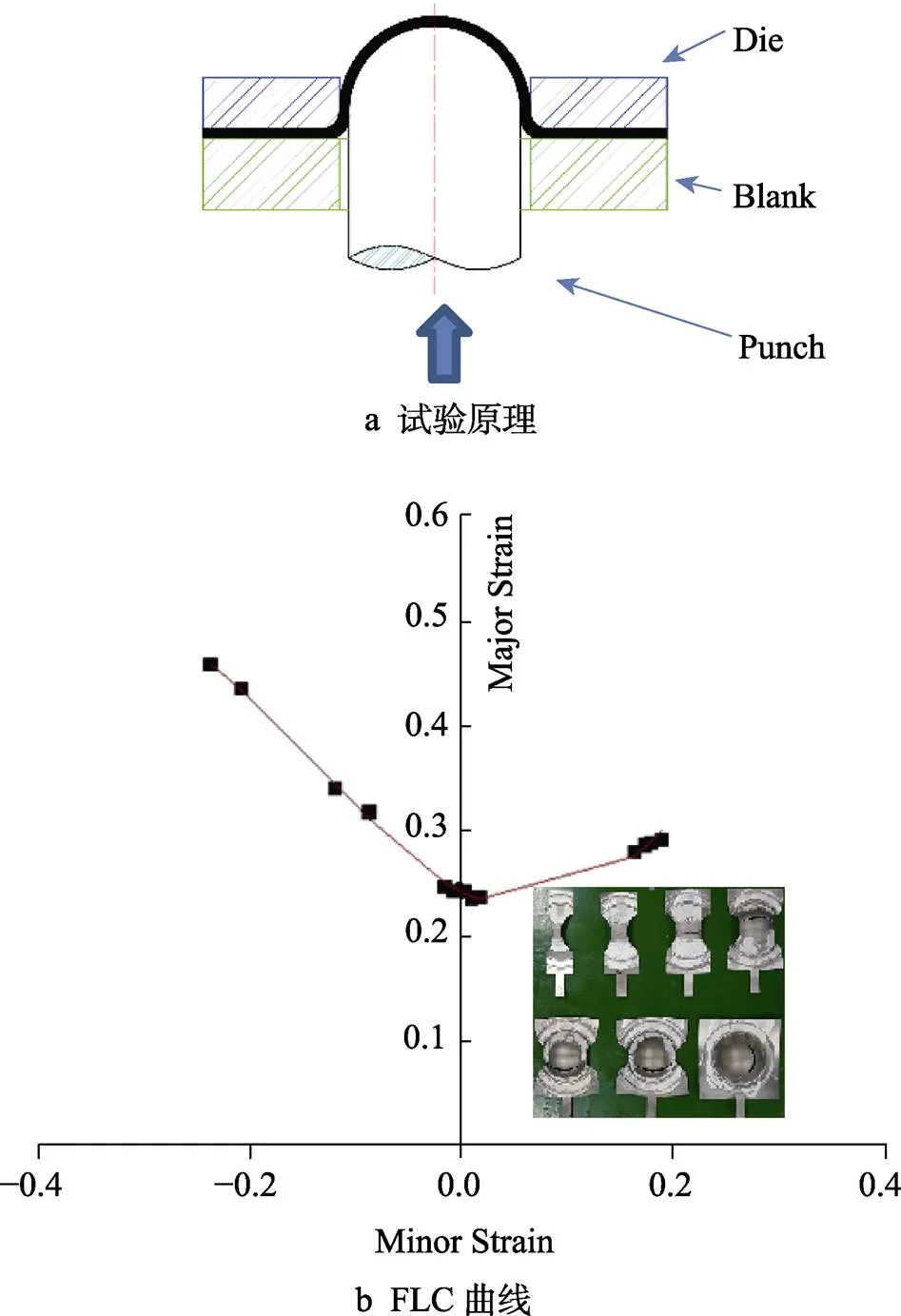
图5 300 ℃的NbTiAl板材成形极限试验

2 M−K理论模型

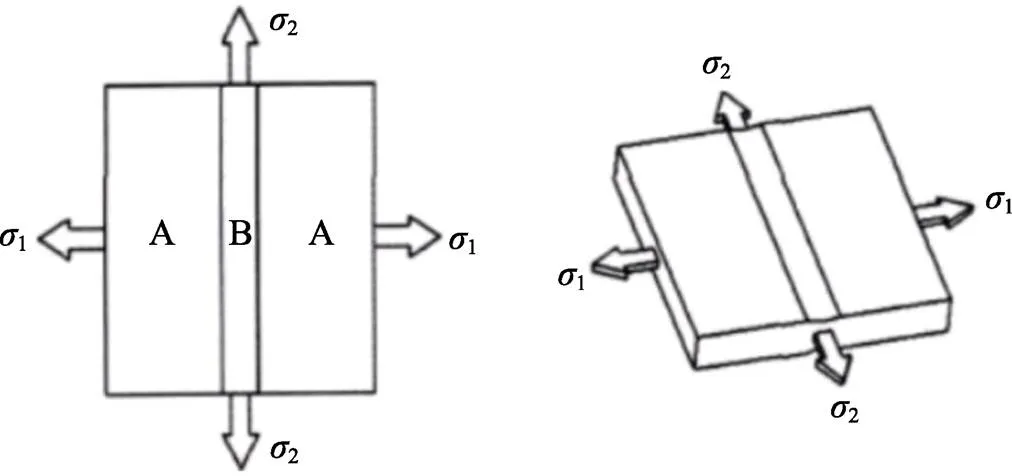
图6 M−K理论模型原理

如图6所示，假设在均匀的A区内存在一个凹槽B区，凹槽B区的存在使得板料有一个初始厚度不均度0，计算见式（1）。

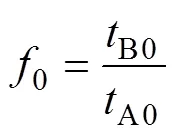
式中：A0与B0分别为板材在模型中的均匀区A区与凹槽区B区的初始厚度。

在初始状态时，需要根据本构方程决定A区和B区的应变，一般存在均为0或者均有一个相同的预应变等2种情况。

考虑到板材的各向异性，采用的是Hill¢48屈服准则，见式（2）。

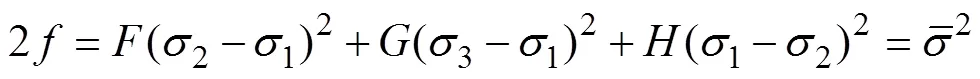
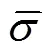
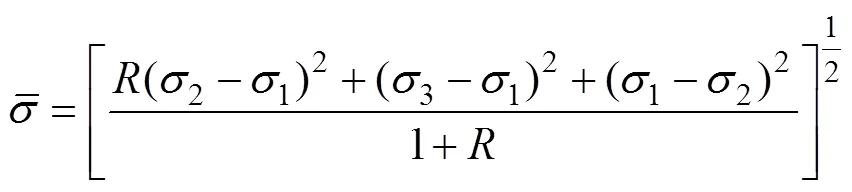
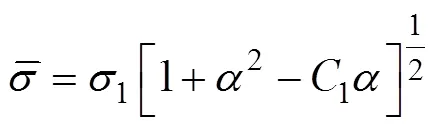
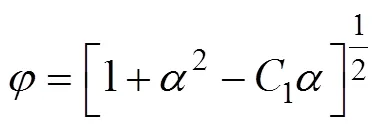
由Levy−Mesis增量理论可得式（6）。

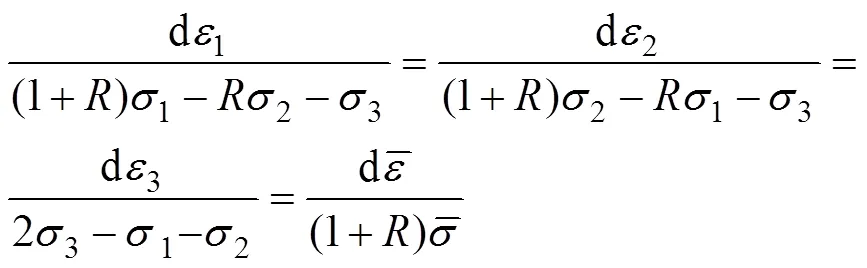
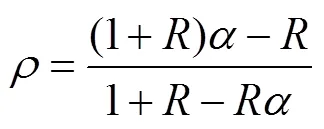
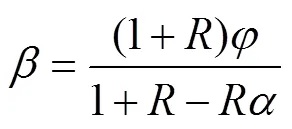
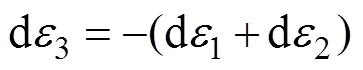
再根据力平衡条件与式（4）可得式（10）。

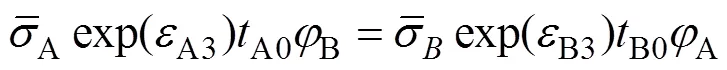
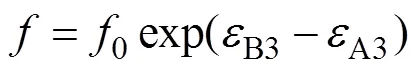
将式（11）代入式（10）可得式（12）。

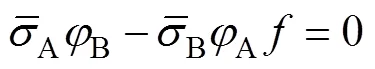
3 成形极限预测与试验结果对比分析

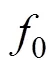
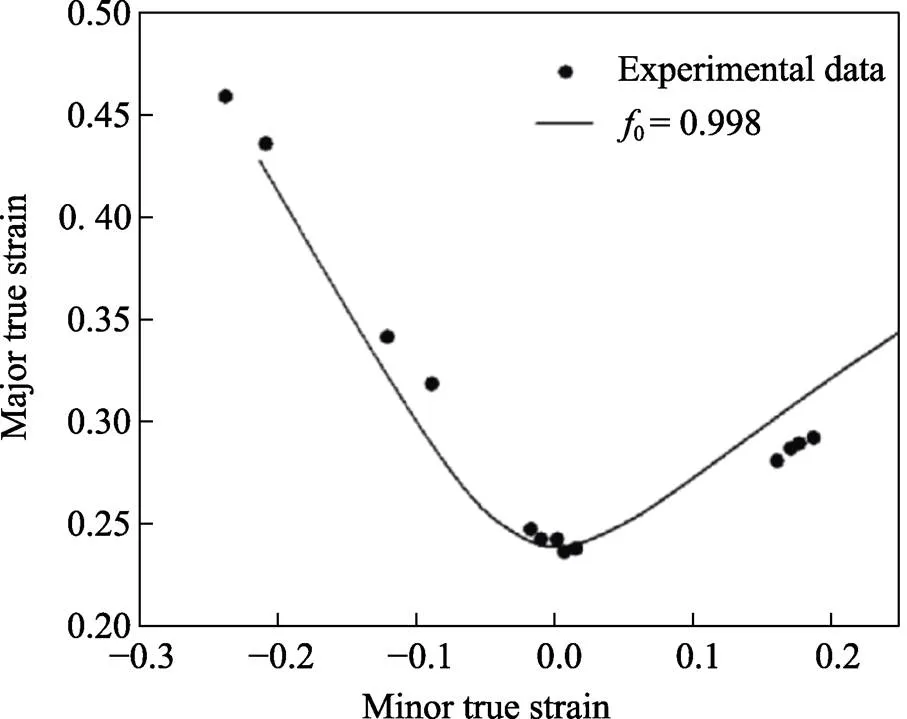
图7 在300 ℃时NbTiAl成形极限理论预测与试验结果对比

4 结论

1）采用高温单向拉伸试验获得了NbTiAl合金在300 ℃的应力应变曲线。NbTiAl合金在300 ℃的塑性应变阶段仍然具有加工硬化效应，其硬化模型可以采用幂函数形式来表示。

2）采用M−K理论对NbTiAl合金高温成形极限曲线进行了预测，并与试验结果进行了对比分析。采用合适的不均匀度系数，M−K理论可以较好地预测NbTiAl合金高温成形极限曲线左侧拉−压区的极限应变，但是对右侧拉−拉区极限应变的预测结果误差较大。

[1] 余宸旭. Nb−Ti−Al高温合金的制备与研究[D]. 长沙: 中南大学, 2013: 1-10.

YU Chen-xu. Preparation and research of Nb-Ti-Al superalloy[D]. Changsha: Central South University, 2013: 1-10.

[2] 史志武, 张洪宇, 韦华, 等. Nb−Ti−Al基超高温合金研究进展[J]. 稀有金属, 2016, 40(2): 172-181.

SHI Zhi-wu, ZHANG Hong-yu, WEI Hua, et al. Progress in Investigation of Nb-Ti-Al Based Ultrahign-Temperature Alloys[J]. Chinese journal of rare metals, 2016, 40(2): 172-181.

[3] 朱宝辉, 吴向东, 万敏, 等. 航天用高温铌基合金进展[J/OL]. 中国有色金属学报: 1-33[2022-05-18]. http://kns.cnki.net/kcms/detail/43.1238.tg.20220419.1028.002.html.

ZHU Bao-hui, WU Xiang-dong, WAN Min,et al. Development of High temperature niobium based alloys for aerospace applications[J/OL]. The Chinese Journal of Nonferrous Metals: 1-33[2022-05-18]. http://kns.cnki. net/kcms/detail/43.1238.tg.20220419.1028.002.html.

[4] 杨希英, 郎利辉, 刘康宁, 等. 基于修正M−K模型的铝合金板材成形极限图预测[J]. 北京航空航天大学学报, 2015, 41(4): 675-679.

Yang Xi-ying, Lang Li-hui, LIU Kang-ning, et al. Prediction of Forming Limit Diagram of AA7075-O Aluminum Alloy Sheet Based on Modified M-K Model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 675-679.

[5] Da-Rocha A B, Santos A D, Teixeira P, et al. Analysis of Plastic Flow Localization Under Strain Paths Changes and Its Coupling With Finite Element Simulation in Sheet Metal Forming[J]. Mater Process Technol, 2009, 209(11): 5097.

[6] Park J J, Kim Y H. Fundamental Studies on the Incremental Sheet Metal Forming Technique[J]. Mater Process Technol, 2003, 140(1/2/3): 447.

[7] Jain M, Allin J, Lloyd D J. Fracture Limit Prediction Using Ductile Fracture Criteria for Forming of an Automotive Aluminum Sheet[J]. Int J Mech Sci, 1999, 41: 1273.

[8] Arrieux R. Determination and Use of the Forming Limit Stress Diagrams in Sheet Metal Forming[J]. Mater Process Technol, 1995, 53: 47.

[9] 傅垒, 李利, 刘成, 等. 基于M−K理论的5182铝合金汽车板成形极限预测[J]. 轻合金加工技术, 2020, 48(7): 58-62.

FU Lei, LI Li, LIU Cheng, et al. Prediction of Forming Limit of 5182 Aluminum Alloy Sheet for Automobile Based on M-K Theory[J]. Light Alloy Fabrication Technology, 2020, 48(7): 58-62.

[10] Swift H W. Plastic Instability Under Plane Stress[J]. Journal of the Mechanics and Physics of Solid, 1952, 1(1): 1-18.

[11] Hill R. On Discontinuous Plastic States with Special Reference to Localized Necking in Thin Sheets [J]. Journal of Mechanics and Physics of Solids, 1952, 1(1): 19-31.

[12] STӦREN S, Rice J.Localized Necking in Thin Sheets[J]. Journal of the Mechanics and Physics of Solid, 1975, 23(6): 421-441.

[13] Zhu X H, Weinmann K, Chandra A. A Unified Bifurcation Analysis of Sheet Metal Forming Limits [J]. Journal of Engineering Materials and Technology. 2001, 123(3): 329-333.

[14] MARCINIAK Z, KUCZYNSKI K. Limit Strains in the Processes of Stretch-Forming Sheet Metal[J]. International Journal of Mechanical Sciences, 1967, 9(9): 609-620.

[15] GANJIANI M, ASSEMPOUR A. An Improved Analytical Approach for Determination of Forming Limit Diagrams Considering the Effects of Yield Functions[J]. Journal of Materials Processing Technology, 2007, 182(1/2/3): 598-607.

[16] Allwood J M, Shouler D R. Generalised Forming Limit Diagrams Showing Increased Forming Limits with Non-Planar Stress States[J]. International Journal of Plasticity, 2009, 25(7): 1207-1230.

[17] 杨晓明, 王宝雨, 校文超, 等. 基于M-K理论的6016铝合金成形极限曲线预测[J].工程科学学报, 2018,40(4): 485-491.

YANG Xiao-ming, WANG Bao-yu, XIAO Wen-chao, et al. Prediction of Forming Limit Curve of 6016 Aluminum Alloy Based on M-K Theory[J]. Chinese Journal of Engineering, 2018, 40(4): 485-491.

[18] 马高山, 万敏, 吴向东. 5A90铝锂合金热态下的成形极限图及其计算模型[J]. 中国有色金属学报, 2008(4): 717-721.

MA Gao-shan, WAN Min, WU Xiang-dong. Theoretical prediction of FLDs for Al-Li alloy at elevated temperature based on M-K model [J]. The Chinese Journal of Nonferrous Metals, 2008(4): 717-721.

[19] 毕静, 马博林, 张艳苓, 等. 基于M−K模型的TA15钛合金高温成形极限[J]. 北京航空航天大学学报, 2020, 46(5): 893—899.

BI Jing, MA Bo-lin, ZHANG Yan-ling, et al. Hot Forming Limit of TA15 Titanium Alloy Based on M-K Model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(0): 893-899.

[20] 余海燕, 高云凯. 基于M−K模型的相变诱发塑性钢板的成形极限研究[J]. 中国机械工程, 2007(1): 109-113.

YU Hai-yan, GAO Yun-kai. Study on Forming Limit Diagram for Transformation-induced Plasticity Sheet Steel Based on M-K Model[J]. China Mechanical engineering, 2007(1): 109-113.

[21] LI Xiao-qiang, DONG Hong-rui, WANG Hai-bo, et al. Effect of Strain Rate Difference Between Inside and Outside Groove in M-K Model in Prediction of Forming Limit Curve of Ti6Al4V at Elevated Temperatures[J]. Transactions of Nonferrous Metals Society of China, 2022, 30(2): 405-416.

[22] Dong Guo-jiang, CHEN Zhi-wei, YANG Zhuo-yun,et al. Domparative Study on Forming Limit Prediction of AA7075-T6 Sheet with M-K Model and Lou-Huh Criterion[J]. Transactions of Nonferrous Metals Society of China,2020,30(6): 1463-1477.

[23] 任丽梅, 张瑞昭, 孔博炜, 等. 基于修正M−K模型的AZ31B镁合金板材预变形前后成形极限预测[J]. 塑性工程学报, 2022, 29(10): 98-105.

Ren Li-mei, Zhang Rui-zhao, Kong Bo-wei, et al. Prediction of Forming Limit of AZ31B Magnesium Alloy Sheet Before and after Pre-deformation Based on Modified M-K Model[J]. Journal of Plasticity Engineering , 2022, 29(10): 98-105.

[24] 王玉宝. 基于M−K理论的金属板料成形极限预测模型的修正及其试验验证与应用[D]. 济南: 山东大学, 2021: 87-88.

Wang Yu-bao. Correction of Sheet Metal Forming Limit Prediction Model Based on M-K Theory and Its Experimental Verification and Application[D]. Ji'nan: Shandong University, 2021: 87-88.

[25] 郑兴悦, 陈劼实. 基于M−K理论的高温成形极限预测及影响因素分析[J]. 模具技术, 2017(6): 1-6.

Zheng Xing-yue, Chen Jie-shi. Prediction of High Temperature Forming Limit and Analysis of Influencing Factors Based on M-K Theory[J].Die and Mould Technology, 2017(6): 1-6.

Prediction of High Temperature forming limit curve of NbTiAl alloy based on M-K theory

MENG Xian-guo1, YAN Jing-kai2, LUO Ya-tao1, ZHOU Bing-ying2, CUI Xue-xi2, WU Xiang-dong2

(1. Xi'an Space Engine Factory, Xi'an 710100, China;2. School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)

The work aims to study the formability of NbTiA alloy at 300 ℃ aiming at the poor plasticity of NbTiAl alloy at room temperature, so as to explore its mechanical properties and forming limit at high temperature, analyze the feasibility of theoretical prediction of forming limit, and provide theoretical reference for further research on the properties of niobium alloy and expansion of its engineering application. The stress-strain curve and forming limit curve of NbTiAl sheet at 300 ℃ were obtained by high temperature single tension test and high temperature forming limit test. The plastic deformation section was fitted by Swift hardening model. The forming limit of NbTiAl alloy at high temperature was theoretically predicted by M-K instability theory and corresponding material constitutive model, and was compared with the test data. NbTiAl alloy still had work hardening effect in the plastic strain stage at 300 ℃. The theoretical curve obtained at the initial thickness non-uniformity0=0.998 was in good agreement with the test point in the left tension-compression zone, but the theoretical prediction results of the tension-tension zone were quite different from the test results. The NbTiAl alloy has good formability at 300 ℃, and the appropriate non-uniformity coefficient combined with M-K theory can predict the limit strain of NbTiAl alloy in the left tension-compression zone of the high temperature forming limit curve, but the prediction error of the limit strain in the right tension-tension zone is large.

NbTiAl alloy; M-K model; high temperature forming limit; plastic instability; theoretical prediction; constitutive equations

10.3969/j.issn.1674-6457.2023.01.001

V261.3+3；TG386.3+2

A

1674-6457(2023)01-0001-07

2022−05−31

2022-05-31

国家自然科学基金面上项目（51875027）

National Natural Science Found Face Items (51875027)

孟宪国（1973—），男，高级工程师，主要研究方向为钣金冲压工艺技术。

MENG Xian-guo (1973-), Male, Senior engineer, Research focus: sheet metal stamping technology.

吴向东（1970—），男，博士，副教授，主要研究方向为先进塑性成形理论与技术。

WU Xiang-dong (1970-), Male, Doctor, Associate professor, Research focus: advanced plastic forming theory and technology.

孟宪国, 闫静锴, 雒亚涛, 等. 基于M−K理论的NbTiAl合金高温成形极限曲线预测[J]. 精密成形工程, 2023, 15(1): 1-7.

MENG Xian-guo, YAN Jing-kai, LUO Ya-tao, et al. Prediction of High Temperature forming limit curve of NbTiAl alloy based on M-K theory[J]. Journal of Netshape Forming Engineering, 2023, 15(1): 1-7.