面向通信成本优化的联邦学习算法

郑 赛，李天瑞*，黄 维

（1.西南交通大学 计算机与人工智能学院，成都 611756；2.云计算与智能技术四川省高校重点实验室（西南交通大学），成都 611756）

0 引言

在过去几年里，机器学习在人工智能应用领域迅速发展，这些机器学习技术尤其是深度学习［1］的成功，都建立在大量数据的基础上。然而，我们在现实世界中遇到的数据往往是小规模的、碎片化的，例如，来自移动终端设备、物联网设备的数据和大量分布在城市中的传感器的数据都拥有这两个特点。出于保护用户隐私和数据安全的要求，简单地将这些数据聚合在一起进行模型训练是不可行的。2018 年，欧盟开始执行《通用数据保护条例》；2021 年11 月，我国开始正式实施《中华人民共和国信息保护法》，国内数据监管法律对数据隐私保护的监管也愈发严格。

联邦学习（Federated Learning，FL）是一种解决上述问题的机器学习设置。联邦学习这一概念由McMahan 等［2］于2017 年首次提出，最近的研究者们对联邦学习提出了一个更宽泛和准确的定义［3］：联邦学习是一种机器学习设置，其中多个客户端在中央服务器或服务提供商的协调下协作解决机器学习问题。每个客户端的原始数据都存储在本地，不进行交换或传输；取而代之的是，使用实时聚合的模型更新来实现学习目标。联邦平均（Federated Averaging，FedAvg）算法是一种典型的联邦学习算法，主要包含两个步骤：客户端接收服务器发送来的全局模型并进行训练得到本地模型；服务器接收来自多个客户端的本地模型，通过加权平均这些本地模型得到一个新的全局模型，再将其发送回客户端。虽然FedAvg 一定程度上解决了联邦学习中的两个核心问题：统计异质性问题和通信成本问题，但是，作为一个朴素的联邦学习算法，它仍然有许多地方可以改进。

本文提出一个结合生成模型和深度迁移学习的联邦学习算法FedGT（Federated Generative Transfer）。该算法只需要客户端和服务器进行一轮通信，能大幅降低联邦学习的通信成本。同时，由于客户端得到了个性化模型，所以统计异质性问题也得到了一定程度的缓解。本文工作的主要特点在于引入生成模型和模拟数据在服务器构建全局模型，并且仅需一轮通信。此前的算法都只传输预测模型参数并进行聚合，而本文算法则通过传输生成模型来生成模拟数据。具体工作如下：

1）利用生成模型在服务器生成模拟数据来建立全局预测模型，可以在一轮通信下保证联邦学习的最终性能。

2）使用深度迁移学习中的微调来进一步适应客户端不同分布的数据，从而缓解统计异质性的问题。

3）在不同的数据集中使用不同的模型进行实验，结果表明本文方法具有一定的通用性。

1 相关工作

1.1 联邦学习

作为一种能够解决数据孤岛和数据隐私安全问题的机器学习设置，相关研究者已经将联邦学习应用到了许多领域：Hard 等［4］将FedAvg 算法用于预测智能手机键盘输入法的下一个单词；史鼎元等［5］将联邦学习应用在信息检索领域，提出了联邦排序学习算法；Muhammad 等［6］将联邦学习应用在推荐系统。然而，联邦学习这一技术的落地仍然面临许多挑战。

联邦学习环境中的客户端通常是来自现实世界的终端设备，例如移动电话、可穿戴设备和智能设备。由于时间、地理位置和用户习惯等因素，这些设备上的数据是非独立同分布（non-Independent and Identically Distributed，non-IID）的，这一问题被称为联邦学习的统计异质性［7］问题。统计异质性导致了一些基于数据独立同分布假设的传统分布式机器学习算法性能低下。为了解决这一问题，联邦学习改进算法被相继提出，例如，FedProx［8］是一个面向统计异质性的算法，它在每个客户端的原有优化目标上增加了一个衡量本地模型和全局模型差异的L2 正则化项，使得模型在non-IID 数据上训练更加稳定，提高了收敛速度。

由于分布在客户端的数据是non-IID 的，这使训练单个全局模型难以适用于所有客户端，所以为每个客户端构建个性化模型十分重要。个性化联邦学习［9］算法通常与迁移学习［10］、知识蒸馏［11］、元学习［12］、多任务学习［13］等其他机器学习技术相结合。迁移学习使深度学习模型能够利用在解决一个问题时获得的知识来解决另一个相关问题，Wang 等［14］利用客户端的本地数据对全局模型参数进行再次更新，从而得到客户端的个性化模型。知识蒸馏通过让学生网络模仿教师网络，将大型教师网络中的知识提取到小型学生网络中，减少了网络的参数量。过拟合是联邦学习个性化模型的一个重要挑战，Yu 等［15］提出将全局模型视为教师、将个性化模型视为学生，通过知识蒸馏来减轻个性化过程中过拟合的影响。Li 等［16］提出了FedMD 算法，这是一个基于知识蒸馏和迁移学习的联邦学习框架，它允许客户端使用本地私有数据集和全球公共数据集单独训练个性化模型。在多任务学习中，多个相关任务被同时解决，模型通过利用各个任务的共性和差异性来达到更好的训练效果。Smith 等［13］表明多任务学习是构建个性化联邦模型的一种合理方式，提出了一个联邦多任务学习框架来应对联邦学习中与通信、掉队和容错相关的挑战。

联邦学习中的另一个核心挑战是高昂的通信成本。现实世界中终端设备数量庞大，通信环境复杂等因素导致了联邦学习的通信压力非常大。为了减少在这种复杂环境下的通信量，面向通信成本优化的联邦学习算法主要从这两方面进行研究：减少客户端和服务器的通信次数；减小每次通信中传输的数据规模。例如，Yao 等［17］在客户端的原有优化目标上增加了基于最大均值差异（Maximum Mean Discrepancy，MMD）距离的加权差异项，通过MMD 距离来衡量全局模型和本地模型的差异，从而加速全局模型的收敛，减少训练过程中的通信次数。而Caldas 等［18］受到常被用于防止模型过拟合的随机失活算法［19］的启发，提出了联邦随机失活算法。在每个全连接层上，该算法丢弃固定数量的全连接层参数，但保证相邻两层失活后的输出矩阵的维度仍然能够进行矩阵运算；而在每个卷积层上，该算法通过丢弃固定数量的卷积核来减少参数。在传统的随机失活算法中，失活后的模型仍然具有和失活前模型一样的大小，而在联邦随机失活算法中，因为只传输激活的参数，所以能显著减少每轮的通信量。除了减少通信次数和减小通信数据规模这两个方面，异步通信［20-21］和通信拓扑优化［22］也是两个重要的面向通信成本优化的研究方向，但是由于实现技术难度大等原因，目前这两个方向的相关研究还较少。

1.2 生成模型

自动编码器（AutoEncoder，AE）和生成对抗网络（Generative Adversarial Net，GAN）［23］是两种著名的生成模型。AE 和GAN 都有许多变体，如变分自动编码器（Variational AutoEncoder，VAE）［24］、WGAN（Wasserstein Generative Adversarial Network）［25］、条件生成对抗网络（Conditional Generative Adversarial Net，CGAN）［26］等。VAE由编码器和解码器组成，编码器将数据样本x编码为隐层表示z，解码器将隐层表示z解码回数据空间，这两个过程可以分别表示为：

VAE 的训练目标是使重建误差尽可能小，即使x和尽可能接近。VAE 损失函数如下所示：

其中DKL指的是KL 散度。

GAN 同样也包含编码器和解码器，通常被称为生成器网络G(z)的解码器将隐层表示z映射到数据空间，同时通常被称为判别器网络D(x)的编码器将训练一个代表数据真实性的概率y=D(x) ∈[0，1]，其中：y越接近1，代表x是真实数据的概率越大；y越接近0，则代表x来自生成器网络G(z)的概率越大。

生成器网络和判别器网络被同时训练：更新G的网络参数来最小化ln( 1-D(G(z)))，更新D的网络参数来最小化ln(D(x))，二者进行着一种两方最大最小博弈（Two-player min-max game），其值函数为：

1.3 深度迁移学习模型

迁移学习可以解决机器学习中训练数据不足的问题，它试图通过放宽训练数据和测试数据必须是独立同分布的假设，将知识从源域转移到目标域。迁移学习的基本方法可以分为四类：基于样本的迁移、基于模型的迁移、基于特征的迁移和基于关系的迁移。基于特征和基于模型的迁移通常表现得更好，这也是目前大多数迁移学习工作的研究热点。由于深度学习在许多研究领域取得了主导地位，研究如何通过深度神经网络有效地转移知识也变得至关重要，这类方法被称为深度迁移学习。深度迁移学习可以分为四类：基于实例的深度迁移学习、基于映射的深度迁移学习、基于网络的深度迁移学习和基于对抗的深度迁移学习。基于网络的深度迁移学习主要通过重复使用在源域中预训练的部分网络来迁移知识，微调［27］就是一种基于网络的深度迁移学习方法，它的主要思想如下：

深度神经网络的浅层通常学习数据的一般性特征，但随着网络的深入，深层网络更注重学习特定性特征。因此，当有一个完成训练的模型时，可以通过冻结浅层网络的参数并更新深层网络的参数，将该模型快速应用于新的数据集或者训练任务。

类似地，在联邦学习中，全局模型学习一般性特征，而局部模型学习特定性特征。可以使用全局模型学习一般性特征，通过微调在每个客户端上学习特定性特征，从而快速训练本地模型。

2 单轮通信联邦学习算法设计

在介绍本文提出的单轮通信联邦学习算法FedGT 之前，先通过介绍FedAvg 算法来了解联邦学习算法的基本流程。

FedAvg 算法的参与者有1 个中心服务器和N个客户端，首先中心服务器要初始化模型参数w0，然后进行T轮迭代：服务器将模型参数发送给随机选出的K个客户端，客户端接收到模型参数对其更新后发回服务器，最后服务器聚合各个客户端的模型参数得到新的模型参数。

算法1 FedAvg 算法。

不同于FedAvg 算法的多轮通信，FedGT 算法仅在客户端和服务器之间进行一轮通信。FedGT 算法主要包括三个步骤：各个客户端利用本地数据训练一个用于生成数据样本的生成模型和一个用于推断标签的局部预测模型，然后将这两个模型的参数发送给服务器；服务器利用各个客户端的生成模型生成数据样本，然后再用客户端的预测模型给这些样本打标签，从而得到一个模拟数据集，服务器再利用该模拟数据集训练一个全局的预测模型并发送给客户端；各个客户端收到全局预测模型后再次利用全局预测模型和本地真实数据训练出个性化本地预测模型。FedGT算法流程如图1所示。

图1 FedGT算法流程Fig.1 Flowchart of FedGT algorithm

2.1 客户端生成模型和预测模型

FedGT 算法会在服务器生成一个模拟数据集，并通过该模拟数据集训练出能代表数据一般性特征的全局预测模型。据我们所知，生成模拟数据的方式通常分为两类：一类为不考虑数据各个维度相关性的分布拟合法；一类为考虑数据各个维度相关性的神经网络生成模型。

分布拟合法可以分为两个步骤：选择不同的数据分布，使用统计方法估计这些分布的参数值；确定哪个分布更加符合数据样本，或者说，选出p值最大的分布作为最终分布。具体地，分布一般由四个参数定义：位置、规模、形状和阈值。这些参数定义了不同的分布：位置参数规定了分布在X轴上的位置；规模参数决定了分布中的扩散程度；形状参数使分布具有不同的形状；阈值参数则定义了分布在X轴上的最小值。分布的参数可以用各种统计方法来估计。例如最大似然估计法通过最小化负对数似然函数值来求得对分布参数的估计值。然后可以采用例如Kolmogorov-Smirnov 检验的方式计算出各个分布在该数据上的p值，选择出p值最大的分布即为最终确定的该数据的分布。

分布拟合法在采用不同分布拟合数据样本时，是对数据的每一个维度进行单独拟合，所以它并没有考虑数据各维度的相关性；而现实世界的数据样本各个维度存在极大的相关性，例如图像数据的邻近像素点，文本数据的上下文都说明数据各维度存在极大相关性。基于深度学习的一些生成模型考虑了数据各维度的相关性，例如典型的全连接层输出特征各个维度在计算时都将输入特征的各个维度乘以权重参数。

这些生成模型通常由编码器和解码器两个部分组成，模型训练的目标为最小化解码器的重建误差。在数据生成阶段，只需将噪声输入到解码器，解码器即可输出生成的模拟数据。VAE 和GAN 主要在编码器和解码器的设计上具有明显差别：VAE 模型参数少，模型结构简单，易于调试，但是在复杂数据上的表现不佳；而GAN 通常可以用于更加复杂的数据的生成，但其模型训练过程参数的调试比较具有挑战性。所以FedGT 算法使用VAE 在简单的数据集上进行实验，而在较复杂的数据集上则采用GAN 进行实验。

建立生成模型可以得到模拟数据样本X，然而仅通过没有标签的数据样本无法建立预测模型，所以客户端需要建立预测模型发送到服务器，从而得到服务器生成的模拟数据的标签Y。本文选取了两个图像分类任务的数据集分别进行实验，客户端的预测模型分别为简单卷积网络（Simple Convolutional Neural Network，Simple-CNN）和修改后的ResNet-18［28］。

2.2 服务器全局预测模型

对于一个客户端，服务器会接收到的内容包括：生成模型的解码器Deci(z)，本地预测模型，数据数量numi。生成模型解码器Deci(z)输入噪声后可以得到模拟数据样本，生成的数量为numi，这些模拟数据会被输入客户端的本地预测模型得到对应的预测值。于是服务器在接受到来自一个客户端的内容后，可以产生一个样本数量为numi的子数据集。当全部N个客户端都发送内容到服务器后，服务器得到N个子数据集后，将这些数据集合并为，使用该数据集训练出全局预测模型Pglobal并将其发送给各个客户端。这些步骤在算法2 中进一步介绍。

2.3 客户端个性化预测模型

FedAvg 和FedProx 等算法在得到全局预测模型后算法就结束了，所以每个客户端最终得到的模型是相同的全局模型；但是由于每个客户端上的数据通常是non-IID 的，同样的模型在某些客户端上表现良好，但在另一些客户端上会表现得很糟糕。对于这个问题，一个更好的解决方案是对于每个客户端单独训练个性化模型。在FedGT 算法中，客户端在接收到全局预测模型后，会利用本地的数据通过微调来得到个性化模型。具体地，客户端会冻结网络模型的浅层网络参数，利用本地数据对深层网络参数进行调整。

算法2 FedGT 算法。

3 实验与结果分析

本文将FedGT 与FedAvg、FedProx 和集中式学习进行了比较。集中式学习是指所有客户端将它们的数据传输到一个中央服务器，然后服务器使用这些数据建立一个全局模型，并将全局模型参数发回给客户端，这种方法的一个重要问题是传输客户端真实数据的同时伴随着数据泄露的风险。

为了说明算法的通用性，分别在CIFAR-10 和MNIST 数据集上采用了不同的生成模型和预测模型进行实验。MNIST 数据集包含了7 × 104张手写数字的灰度图像，所有图像被分为10 类，分别为手写数字0～9，并且每张图像已经被标准化为28 × 28，训练集包含6 × 104张图像，测试集包含1 × 104张图像。CIFAR-10 数据集由6 × 104张32 × 32 的彩色图像组成，所有图像被分为10 类，分别为飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船和卡车，每类有6 × 103张图像，包括5 × 103张训练图像和1 × 103张测试图像，数据集总共有5 × 104张训练图像和1 × 104张测试图像。

3.1 在MNIST数据集上的实验

在MNIST 数据集上使用VAE 作为生成模型，使用Simple-CNN 作为预测模型。Simple-CNN 的结构如表1 所示，除了表1 中提到的卷积层和池化层，使用ReLU 函数作为网络的激活函数，并增加了随机失活层防止过拟合。

表1 Simple-CNN的结构Tab.1 Structure of Simple-CNN

对于数据集在客户端上的划分，采用了IID 和non-IID 两种方式。首先将训练集和测试集合并得到7 × 104张图像，然后设置了20 个客户端，IID 的数据划分方式为：每个客户端互不重复地随机选取3.5 × 103张图像作为本地数据集，其中6/7 被作为本地训练集，1/7 被作为本地测试集。而non-IID 的划分方式为：将所有数据切分成40 份，其中每份数据只包含10 个类别中的1 个类别，每个客户端互不重复地随机选取2 份数据作为本地数据集，这保证了每个客户端上至多有2 种类别的数据，同样地，non-IID 划分的训练集-测试集比例为6∶1。

在FedGT 算法的步骤3 中，客户端接收到全局预测模型进行微调时，冻结Conv1、Conv2 和FC1 这三层的参数，只更新FC2 这一全连接层的参数。使用Adam 作为优化器，使用交叉熵作为损失函数，每批次数据量为64，训练轮数为500，学习率为5 × 10-4。

实验选取了集中式学习，FedAvg、FedProx、FedMD 和FedDyn［29］作为基准算法与FedGT 算法进行比较。其中FedAvg 和FedProx 作为联邦学习中较早发表的经典算法，常被用于各类联邦学习算法实验的基准算法。FedDyn 是目前最新的联邦学习算法，它在客户端本地模型更新的损失函数中加入了一个动态的正则器，使客户端每轮的损失函数动态更新，同时使全局经验损失和局部经验损失的最小值保持渐进一致，FedDyn 算法的通信效率和准确率均优于FedAvg 和FedPox。FedMD 是个性化联邦学习中的一个重要算法，它将知识蒸馏和迁移学习同时运用在联邦学习训练过程中，允许客户端使用本地私有数据集和全球公共数据集单独训练个性化模型。

基准算法在训练过程中使用随机梯度下降（Stochastic Gradient Descent，SGD）作为优化器，使用交叉熵作为损失函数，每批次数据量为64，训练轮次为200，初始学习率为0.1，每50 轮衰减80%。

表2 列出了所选基准算法和FedGT 算法在MNIST 数据集上的准确率，由于集中式学习是将数据集中到服务器上进行训练，所以它在non-IID 划分和IID划分下的准确率是相同的。FedGT 算法在IID 和non-IID 数据划分下的准确率超过了实验对比的所有基准算法，然而不同于基准算法，FedGT 算法在non-IID数据划分下的准确率比IID数据划分的准确率高。

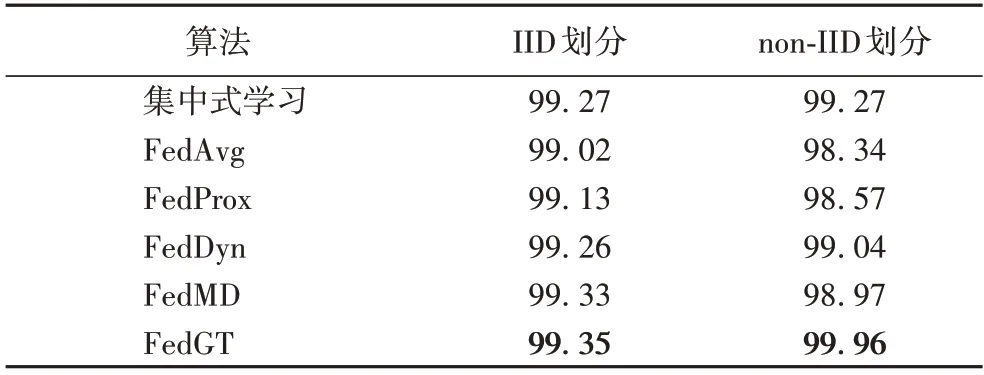
表2 不同算法在MNIST数据集上的准确率 单位：%Tab.2 Accuracies of different algorithms on MNIST dataset unit：%

3.2 在CIFAR-10数据集上的实验

在CIFAR-10 数据集上使用GAN 作为生成模型，采用修改后的ResNet-18 作为预测模型。修改后的ResNet-18 残差单元的结构如图2 所示，图中Conv1、Conv2 和Conv3 即为表3中的Conv1、Conv2 和Conv3。

表3 修改后的ResNet-18网络结构Tab.3 Modified ResNet-18 network structure

图2 修改后的ResNet-18残差单元结构Fig.2 Structure of residual unit of modified ResNet-18

由于ResNet-18 网络输入图像的尺寸为3 × 224 × 224，而CIFAR10 的图像尺寸为3 × 32 × 32，所以对ResNet-18 进行了一定调整，主要改动为：将第一个卷积核为7 × 7 的卷积层以及一个最大池化层替换为一个卷积核为7 × 7 的卷积层，以此来适应CIFAR-10 的图像尺寸，具体网络结构参数如表3 所示。其中：Conv2d（3，1）代表卷积核为3 × 3、步长为1的二维卷积层；ResUnit(n，m，k1，k2，k3)代表一个如图2 所示的残差单元，Conv1、Conv2 和Conv3 的卷积核都为n×n，输出通道都为m，步长分别为k1、k2 和k3；AvgPool（4，4）代表核为4 × 4、步长为4 的平均池化层；Linear（512，10）代表输入为512 维向量、输出为10 维向量的全连接层。

对于数据集在客户端上的划分，采用和在MNIST 数据集上相同的IID 划分和non-IID 划分策略，首先合并训练集和测试集，客户端数量为20，如果为IID 划分则随机选取，如果为non-IID 划分则使每个客户端至多有两个类别的样本，客户端上训练集和测试集的比例保持和原数据集一致，都为5∶1。

客户端接收到全局预测模型进行微调时，冻结ConvIn、Layer1、Layer2 和Layer3 层的参数，只更新Layer4 和Linear。在FedGT 和基准算法上使用的实验参数与在MNIST 上的实验参数一致，表4 列出了实验结果。基准算法在CIFAR-10上的准确率整体上低于MNIST 上的准确率，FedGT 算法的准确率在IID 和non-IID 数据划分上都优于基准算法。

表4 算法在CIFAR-10数据集上的准确率 单位：%Tab.4 Accuracies of algorithms on CIFAR-10 dataset unit：%

3.3 通信效率和计算开销

FedGT 算法的主要目的是减少联邦学习中的通信轮数和通信数据量。通常一个联邦学习模型需要进行E轮通信，每轮通信均传输预测模型参数；而FedGT 算法只需要一轮通信，客户端发送给服务器生成模型解码器和本地预测模型的参数，服务器发送给客户端全局预测模型参数。表5 中对比了FedGT 和基准算法在两个数据集上的通信量。由表5 可以看出：在MNIST 数据集上，FedGT 算法的通信量约为FedAvg、FedProx、FedDyn 算法通信量的1/10，约为FedMD 算法的1/100；在CIFAR-10 数据集上，FedGT 算法的通信量约为FedAvg、FedProx、FedDyn 算法的通信量的1/100，约为FedMD算法的1/10。

表5 MNIST和CIFAR-10数据集上的通信效率对比Tab.5 Comparison of communication efficiency on MNIST and CIFAR-10 datasets

联邦学习通信成本的减少会带来计算量的增加，本文以每秒浮点运算次数（Floating-Point Operations Per Second，FLOPS）为单位计算了模型在前向和反向传播时的计算量，并考虑了损失函数不同对反向传播过程中计算量的影响和服务器端聚合模型的计算开销，最终得到的计算量如表6 所示，其中客户端这一栏为单个客户端的计算开销。计算结果显示，FedGT 算法增加了联邦学习在服务器上的计算开销，但减少了客户端上的计算开销。联邦学习的客户端通常为移动智能设备，只有当设备空闲时才能进行模型训练，而这些设备计算能力远不如计算能力强大的服务器，所以FedGT算法减少客户端计算开销、增加服务器计算开销有利于联邦学习的落地。

表6 MNIST和CIFAR-10数据集上的计算开销对比 单位：FLOPsTab.6 Comparison of computing overhead on MNIST and CIFAR-10 datasets unit unit：FLOPs

4 结语

本文提出了一种新的联邦学习算法——FedGT 算法。该算法采用服务器生成模拟数据来训练全局模型，这一做法能够将通信的轮数减少至一轮，并且还在客户端通过模型的微调实现模型个性化来解决客户端异质性问题。FedGT 算法在不同的数据集上使用不同的架构进行了实验，结果表明它在数据以IID 和non-IID 方式分布时均优于FedAvg、FedProx、FedDyn 和FedMD 算法。

FedGT 算法为联邦学习的研究提出了一个新的方向：除了传输目标训练模型的参数，还可以传输其他信息（例如生成模型）来加快模型训练，减少通信轮数，这是一个新颖且具有挑战的研究方向。我们的下一步研究工作是在更广泛的数据集上检验FedGT 算法，这样才能真正捕捉到联邦学习真实场景下的大规模分布的复杂性。