变长度柔性双足机器人行走控制及稳定性分析
2023-02-03廖发康周亚丽张奇志
廖发康,周亚丽,张奇志
(北京信息科技大学 自动化学院,北京 100192)
0 引言
1990 年,McGeer[1]提出了被动动态行走(Passive Dynamic Walking,PDW)模型,在双足机器人领域取得了里程碑意义的研究成果。与主动控制系统[2]相比,基于PDW原理设计的机器人效率要高得多,因为此类机器人的运动是通过腿的自然摆动来维持的,而不是通过安装在每个关节上的电机来驱动的。但是被动行走步态单一,抗扰性能较差,容易出现混沌特性,进入不稳定状态[3];而且由于摆动腿落地瞬间,与地面之间的冲击存在能量损失,采用刚性腿的被动行走机器人不能在水平面上持续行走,且刚性腿太僵硬,不具有拟人性。1989 年,Blickhan[4]首次提出了弹簧-质点模型,用以描述人类的奔跑和跳跃。研究表明触地时间和跳跃频率不是简单地由弹簧-质量系统的固有频率决定的,而是很大程度上受着陆速度矢量的影响。虽然人类的腿具有复杂的神经控制系统,但在跑步阶段,腿会表现出简单的弹簧状行为,可以用弹簧-质点模型来描述。2006 年,Geyer 等[5]对弹簧-质点模型进行扩展,该模型将双支撑作为行走过程中的重要组成部分,用简单的弹簧负载倒立摆(Spring-Loaded Inverted Pendulum,SLIP)模型模拟了人类在平面上的运动。Geyer 的研究表明:带弹簧的柔性腿可以准确地再现人体行走过程中髋关节运动轨迹和站立时的动力学特性。双足机器人采用柔性腿代替刚性腿,借助于弹簧的弹性势能,可以实现平地上的类人行走。2010 年,Rummel 等[6]通过对机器人行走时腿部刚度与鲁棒性之间的关系研究,得出了可变腿刚度能有效地抑制外部干扰的结论。2012 年,Visser等[7]把SLIP 扩展为变腿刚度模型(Variable leg stiffness-SLIP,V-SLIP),显著提高了双足机器人对外界干扰的鲁棒性。2013 年,Visser 等[8]将V-SLIP 模型扩展为考虑摆动腿动力学的V-SLIP 模型(V-SLIP model with Swing Leg dynamics,V-SLIP-SL),即在每条腿的末端增加了一个脚质量。仿真结果表明,在控制器的作用下,机器人具有足够的鲁棒性,能够抑制由摆动腿动态所引起的扰动。2020 年,Pelit 等[9]以被动SLIP-SL 模型作为模板,为5 连杆全驱动双足机器人的质心和摆动脚提供所需的轨迹。仿真结果表明,该控制器可以跟踪由SLIP-SL 模型获得的轨迹,并且简单的SLIP-SL 模型比高自由度模型在计算方面更有优势。
尽管双足机器人的扩展及变刚度控制能使机器人拥有良好的鲁棒性能,但变刚度实验装置的设计和制造[10-11]都比较复杂,而变长度的实验装置要简单得多[12]。2008 年,Asano 等[13]针对平面伸缩腿双足机器人模型,提出了一种简单的控制律,在不考虑零力矩点(Zero Moment Point,ZMP)条件的情况下,通过伸缩摆动腿即可轻松实现水平步态生成。2012 年,Asano[14]引入了一个由8 个伸缩腿组成的平面无缘轮模型,并将该方法推广到带有制动弹簧的平面伸缩腿双足机器人,通过数值仿真验证了该方法的有效性。2018年,Harata 等[15]研究了包含伸缩腿的欠驱动双足机器人的稳定性。将输出跟随控制律应用于机器人的线性化运动方程中,将被控机器人的运动方程指定为一个线性时变系统,建立了误差转移方程来评估稳定性,通过数值计算说明了腿部伸缩运动对稳定性的影响。
上述文献的变长度伸缩腿控制基本采用的都是刚性腿,本课题组在此基础上,对双足机器人变长度的柔性伸缩腿控制展开研究。2019 年,张奇志等[16]研究半被动伸缩腿双足机器人行走控制和周期解的全局稳定性问题,设计了腿伸缩长度的支撑腿角度反馈控制率,证明了伸缩腿双足机器人行走过程不动点的全局稳定性;同年,宋嘉琦等[17]采用变长度柔性伸缩腿结构,研究了半被动双足机器人的平面稳定行走的控制问题,结果表明变长度控制算法可以实现机器人的稳定行走,并具有较强的抗干扰性。2022 年,张瑞等[18]用半被动变长度弹性伸缩腿双足机器人模型,提出了一种基于能量的仿人控制方法。结果表明,所提出的控制策略可使双足机器人在水平面上实现起步行走过程,并对外部的扰动具有一定的抗扰性。
本文在上述研究成果的基础上,提出了考虑躯干影响和摆动腿动力学的变腿长度柔性双足机器人(Variable Leg length SLIP with Torso and Swing Legs dynamics,VL-TSLIPSL)模型。首先,建立柔性双足机器人的动力学模型,仿真求解出双足机器人被动行走的自然步态,将其作为期望步态;其次,采用反馈线性化控制方法,通过对双足机器人腿长度变量和髋关节力矩的控制,实现机器人的稳定周期行走;最后,采用Newton-Raphson 迭代法和庞加莱映射相结合,求解不动点并分析系统的稳定性。
1 双足机器人动力学模型
1.1 机器人模型描述
双足机器人的模型如图1 所示。由质量为M的髋关节质点、中心质量为m的刚性杆及两条长度可变的柔性腿组成,每条腿的末端各有一个脚质量mf。髋关节质点坐标为[x,y]=:qh∈Qh,其中Qh表示二维的实数域。躯干长度为l,转动惯量为I;腿长度为L0+ui,L0为原长度,ui(i=1,2)为可控的长度增量。两腿各有一个弹性系数为k0的单向弹簧。髋关节力矩τ1和τ2用来控制躯干姿态角α和摆动腿与法线夹角β。

图1 VL-TSLIP-SL模型Fig.1 VL-TSLIP-SL model
图2 为机器人的运动过程。其初始状态是左腿作支撑腿,右腿作摆动腿,呈垂直站立(Vertical Leg Orientation,VLO)状态,摆动腿不与地面接触,此时为单支撑(Single Support,SS)阶段。当髋关节下降到高度S时,此时的S=L0sinθ称为切换高度,摆动腿以原始长度L0和角度θ接触地面,然后机器人进入双支撑(Double Support,DS)阶段。当髋关节升高到高度S时,系统再次进入SS 阶段,左腿变为摆动腿,右腿变为支撑腿,考虑到双腿的对称性,图2 中所表示的从左腿作支撑腿到右腿作支撑腿的过程称为机器人的一个步态周期,如此循环反复。

图2 双足机器人的运动过程Fig.2 Moving process of biped robot
由此可得,从SS 过渡到DS 的条件是:

DS 切换为SS 的条件为:

其中Li是后支撑腿的长度。
1.2 系统动力学模型
在图1 中,以支撑腿与地面的接触点为坐标原点O,建立图中所示直角坐标系,利用拉格朗日方程建立系统的动力学方程。定义拉格朗日函数为:

其中:K为系统的动能,P为系统的势能。
系统动力学方程为:

其中:n为系统的自由度,qi为系统的变量,Fi为作用于系统的广义力。
1.2.1 单支撑阶段的动力学方程
SS 阶段的简化模型如图3 所示。右腿是摆动腿,长度为L0,与法线夹角为β,因为在此阶段不需要对右腿进行变长度控制,所以假设为刚性腿。在这个阶段,左腿长度增量为u1,力矩τ1和τ2是控制髋关节质点运动,躯干姿态角和摆动腿夹角的控制输入,系统状态变量为[x,y,α,β]T=:qSS∈QSS(QSS={qSS∈QSS|L0sinθ<y<L0})。

图3 SS阶段的简化模型Fig.3 Simplified model of SS phase
分别计算系统的动能K和势能P,可得拉格朗日函数的表达式为:


1.2.2 双支撑阶段的动力学方程
DS 阶段的简化模型如图4 所示。此时双腿接触地面,由于右腿与法线的夹角β可以通过髋关节位置和脚触地点计算得到,因此系统的状态变量为[x,y,α]T=:qDS∈QDS。在这个阶段中,双腿长度增量u1、u2和力矩τ1是控制髋关节运动和躯干姿态角的控制输入,其中QDS为QDS={qDS∈QDS| 0 <y≤L0sinθ}。

图4 DS阶段的简化模型Fig.4 Simplified model of DS phase
采用与SS 阶段相同的推导方法,得到DS 阶段的动力学方程:


由式(9)~(10)可知,系统在SS 阶段为欠驱动模型,在DS 阶段为全驱动模型,但总的来说,系统是欠驱动系统。
1.3 状态空间表达式
为了便于后续的反馈线性化控制器的设计,在这里将动力学方程转换为标准的状态空间表达式。在SS 阶段,令:

2 控制器设计
2.1 控制目标
对于文中所要研究的双足机器人,设定的控制目标是:在保证躯干直立的情况下,使髋关节质点跟踪期望高度y*(x)和期望水平速度,并使摆动腿按期望轨迹β*(x)摆动。由于机器人在稳定行走过程中,水平位置x在时间上是严格单调递增的,因此本文采用x替代时间t作为自变量,即采用空间轨迹方法。


为了避免符号混乱,省略函数参数z1。定义控制目标的误差函数为:

控制目标是使误差尽可能收敛到0 的邻域。
2.2 反馈线性化控制
本文通过反馈线性化方法设计控制器,来控制腿的伸缩长度和髋关节力矩,使机器人的行走能够逐渐逼近期望的步态,躯干倾角和摆动腿夹角收敛到期望角度。需要说明的是:由于系统在SS 阶段有4 个自由度,但是只有3 个控制输入,属于欠驱动状态,因此采用部分反馈线性化(Partial Feedback Linearization,PFL)的控制方式[19],水平方向速度误差ev在SS 阶段不受控制。在DS 阶段,两脚都与地面接触,不需要对误差eβ的动态控制,属于全驱动状态,因此采用标准反馈线性化的控制方式。考虑到在单支撑阶段,不是用3个控制输入控制4 个被控变量;而是用3 个控制输入控制3个被控变量,另一个被控量不控制,所以单支撑欠驱动和双支撑全驱动的反馈线性化控制器的设计是一样的。
2.2.1 单支撑阶段
在SS 阶段,控制变量为髋关节高度轨迹y、躯干姿态角α和摆动腿夹角β,则系统的状态空间表达式为:

为了将该非线性系统转换为线性标准型,首先需要确定误差的关系度γSS={γp,γα,γβ}。
对于位置误差ep:


所以关系度γp=2,同理可得γα和γβ的关系度也为2。因此,在SS 阶段中,误差的关系度γSS={γp,γα,γβ}={2,2,2}。
根据反馈线性化原理,可得误差动力学方程为:

2.2.2 双支撑阶段
在DS 阶段,控制变量为髋关节高度y、躯干姿态角α和前进速度x˙。采用与SS 阶段相同的方法,可以得到关系度γDS={γp,γα,γv}={2,2,1},则误差动力学方程为:

3 轨道稳定性分析
被动行走周期步态的特点是系统的状态变量每隔一个周期重复取值一次,在状态空间中表现为周期轨道,又称极限环,因此被动行走周期步态的局部稳定性采用轨道稳定性来定义。从直观上讲,周期步态是轨道稳定的是指周期轨道对应的某个状态受到有限扰动后偏离了原有的周期轨道,但系统的状态最终运动到其附近的一条周期轨道上。如果状态受到扰动后,系统在自身的作用下仍能回到原来所在的周期轨道上则称周期步态是轨道渐近稳定的。
分析周期轨道稳定性的常用办法是通过庞加莱映射(Poincaré map)将周期轨道稳定性问题转化为不动点的稳定性问题[20-21]。本文将摆动腿触地瞬间所在的超平面取为庞加莱截面Σ,两个连续触地事件之间的关系可以用庞加莱映射表示为P:Σ→Σ,即

其中:P代表庞加莱映射,为庞加莱截面上的6 维状态变量。状态变量不包含髋关节位置(x,y),这是因为水平位置x为自变量,垂直位置y可由y=L0sinθ计算得到。因此,选择合适的庞加莱节截面及采用空间轨迹的分析方法,可以将状态变量维数由8 维降低到6 维,可以有效降低算法的复杂性及运算量。
对于周期相位轨迹,庞加莱截面上的状态变量为常数,即

其中:φ*为庞加莱映射的不动点。因此,通过庞加莱映射,双足机器人的稳定性问题转换为庞加莱映射不动点的稳定性问题。
3.1 求解不动点
求解庞加莱映射不动点的常用方法是Newton-Raphson迭代法。用φk表示轨道第k次穿过庞加莱截面的点,由式(19)可知φk+1=P(φk),设φk+1=φk+Δφk,利用一阶泰勒公式对庞加莱映射函数P(x)进行局部线性化,可以得到如下关系:

使用φk+1=φk+Δφk进行迭代,直到Δφk小于给定的阈值误差,便求得不动点φ*。
3.2 轨道稳定性判据
对于不动点φ*附近的小扰动Δφ*,采用泰勒级数展开,庞加莱映射函数可以表示为:

其中:∇P为庞加莱映射函数相对于系统状态的梯度,称为雅可比矩阵。∇P其表达式为:

该矩阵的特征值λ称为被动行走系统的Floquet 乘子。由于Δφk+1=(∇P)Δφk,所以,当雅可比矩阵的所有特征值满足|λ| <1 时,必有<1,即随着k的增加,Δφk→0,误差会随着步长的增加而逐渐减小,极限环将逐渐收敛到原周期轨道,由轨道稳定性定义可知系统的周期步态是轨道稳定的。
4 仿真分析


表1 系统参数和初始条件Tab.1 System parameters and initial conditions
4.1 步态分析
图5 给出的是髋关节轨迹、躯干姿态角α和摆动腿夹角β的轨迹图。可以看出,所提出的控制器能够维持稳定的周期步态,并保持躯干直立。从图6 中可以看出,得到的误差曲线收敛于零的邻域。在DS 阶段,因为摆动腿角度β在此阶段没有定义,所以eβ≡0。此外,如前所述,系统在SS 阶段处于欠驱动状态,采用的是部分反馈线性化的控制方式。即仅在DS 阶段控制髋关节质点的水平速度。从图6(d)中可以看出:误差ev在DS 阶段趋于零,而在单支撑阶段,存在一定的误差。

图5 髋关节轨迹、躯干倾角轨迹和摆动腿夹角轨迹Fig.5 Hip trajectories,torso attitude angle trajectory,and swing leg included angle trajectory
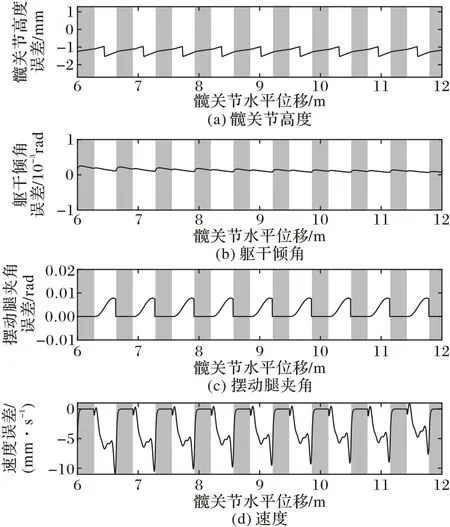
图6 稳态误差变化曲线(灰色区域为DS阶段)Fig.6 Error change curves in steady state(the areas printed in grey are DS phases)
图7 给出了稳定状态下的控制输入变化曲线,黑色虚线对应腿原长度(L0=1 m)。理想的SLIP 参考模型可以在没有任何控制输入的情况下(即u1=u2=0)维持稳定的步态。本文提出的VL-TSLIP-SL 模型包括躯干姿态和摆动腿控制,这些非理想动态都被认为是系统的外部扰动,因此需要较大的控制输入来抑制这些扰动。在图7 中可以清楚地看到控制输入随着机器人的行走作出的变化,由于摆动腿夹角β在DS 阶段没有定义,所以在DS 阶段τ2≡0。此外,由于在行走的过程中,左右腿交替作为摆动腿,所以在SS 阶段,控制输入u1和u2交替为零。

图7 稳态控制输入变化曲线Fig.7 Control input change curves in steady state
系统的能量曲线如图8 所示,其中虚线为理想SLIP 模型的能量水平。可以看出,总能量在SLIP 模型的能量水平上波动。一方面原因是控制器作用在躯干和摆动腿上,需要消耗能量;另一方面原因是期望轨迹由傅里叶级数拟合而来,存在着一定的偏差。因此,实际上能量水平不是恒值,存在一定的波动。

图8 系统的能量曲线Fig.8 Energy curves of system
4.2 稳定性验证
4.2.1 特征值分布
对于雅可比矩阵,由于无法得到解析解,在实际的机器人系统中,通常采用数值方法进行求解。数值解法的步骤如下:
步骤1 用Newton-Raphson 迭代法得到不动点φ*=
步骤2 每次对一个状态变量施加扰动,其他状态变量保持不变。
步骤3 观察庞加莱映射的首次返回值。
步骤4 计算式(25)中对应列的元素值。
步骤5 重复6 次,即每个状态变量各1 次。
步骤6 计算雅可比矩阵的特征值,判断系统是否稳定。
对于本文提出的双足机器人系统,存在一个不动φ*=(0.000 3,1.090 8,1.147 6,-1.058 8,0.000 6,0.010 5)T,对不动点施加一个大小为1 × 10-3的小扰动,则雅可比矩阵为:

计算特征值为:-0.050 7+0.000 0i;-0.000 2+0.0000i;0.482 9+0.427 5i;0.482 9-0.427 5i;0.347 1;0.0042。
其最大特征值的模为0.644 9<1,因此不动点φ*是稳定的,该系统是轨道稳定的。
4.2.2 极限环
图9 给出了双足机器人以稳定的周期步态行走足够长的时间后的相位轨迹。由于机器人双腿步态的对称性,双腿交替为支撑腿与摆动腿,因此只画出了从左腿以原长触地瞬间到右腿以原长触地瞬间的极限环。在极限环之外,本文用小棍图来表示双足机器人行走的步态,脚末端的黑点表示腿与地面接触。相位轨迹的循环方向用箭头表示。
阶段Ⅰ:A点到B点(DS阶段)。
如图9(a)所示,从标记为A 的瞬间,即机器人单双支撑切换瞬间开始行走,(也就是左腿以原长刚接触地面变为支撑腿时刻),此时机器人处于DS 状态。A 点位于庞加莱截面上,因此髋关节质点的水平速度==1.147 6 m/s。由于系统有足够的能量,它将继续向前移动,伸展左腿,直到达到其原长度(点B)。

图9 系统的相位轨迹Fig.9 Phase trajectories of system
阶段Ⅱ:B点到C点(SS阶段)。
在B 点瞬间,左腿失去与地面的接触,以原长向前摆动,机器人从DS 阶段切换到右腿SS 阶段。可见B 点也在庞加莱截面上,因此髋关节质点的水平速度=1.147 6 m/s。当机器人到达C 点时,右腿垂直站立,左腿处于摆动阶段。
阶段Ⅲ:C点到D点(SS阶段)。
在C 点,机器人系统处于VLO 状态。为保证步态对称,髋关节质点的垂直速度=0 m/s。右腿保持与地面接触,左腿继续向前摆动。当机器人到达D 点时,左腿以其原长度接触地面,双足机器人从右腿SS 阶段切换到DS 阶段。然后两条腿互换角色,相位轨迹回到下一个行走阶段的A 点(实际上,A 点和D 点是同一点)。
图9(b)为三维相位轨迹,可以更直观地看出,随着机器人按照x轴方向的行走,极限环依次螺旋上升,系统状态变量已形成稳定的极限环,双足机器人处于稳定运行状态。
从特征值的计算及图9 的相轨迹可以看出,虽然在单支撑阶段采用了部分反馈线性化控制方法,但是雅可比矩阵的特征值均位于单位圆内,形成稳定的极限环,证明系统是轨道稳定的。
4.3 扰动抑制性能
为了验证控制策略在扰动下的有效性,在x=3.692 m处,施加Fd=[Fx,Fy]T=(10,20)TN 的扰动,持续0.644 3 m,结果如图10 所示。
在图10 中,虚线表示对系统施加扰动的瞬间。可以看出,系统在扰动下能够保持稳定的步态,经过一个短暂的过渡阶段后,系统恢复到稳定的周期步态。对于髋关节高度y,由于采用的是变腿长度控制,机器人在受到扰动时,控制器控制伸缩腿,使系统能保持在原有的期望轨迹上;对于前进速度x˙和躯干α,大约在2 步内收敛到期望轨迹;对于摆动腿夹角β,大约在4 步内收敛到期望轨迹。总体上来看,机器人能够抵抗外部扰动,继续平稳地行走。

图10 系统受到扰动后的响应Fig.10 Response of system after disturbance
为了进一步研究变长度控制器的性能,对机器人施加不同的干扰,通过重复性实验研究其扰动抑制区域。考虑到实际情况,干扰力限制在±100 N 内。结果如图11 所示。深灰色区域为无变长度情况下的抗干扰区域,浅灰色区域为变长度情况下的抗干扰区域。对于图11(a),当机器人处于SS 阶段时,在3.692 m 处施加扰动;对于图11(b),当机器人处于DS 阶段时,在5.996 m 处施加扰动。可得出,系统处于DS 阶段的抗干扰性能优于SS 阶段,这是因为系统在SS 阶段为欠驱动,在DS 阶段为全驱动。总体而言,该控制方法对扰动具有较好的鲁棒性。

图11 系统对不同扰动力的响应Fig.11 Response of system to different disturbance force
5 结语
本文提出了VL-TSLIP-SL 模型,该模型由一个髋关节质点、一个刚性躯干和两条柔性腿组成,每条腿的末端都有一个脚质量。本模型包含了躯干姿势控制和摆动腿动力学。利用拉格朗日第二方程构造机器人的动力学方程,通过控制双腿长度,控制机器人的实际步态轨迹逐渐收敛到期望步态轨迹。由于系统的高耦合和非线性特点,采用反馈线性化的方法将非线性系统转换为线性系统,实现机器人的步态渐近稳定。利用Newton-Raphson 迭代法结合庞加莱映射分析可知,双足机器人周期轨道的稳定性等价于庞加莱映射不动点的稳定性。最后,通过数值仿真验证了其轨道稳定性和抗干扰性能。未来的工作将进一步研究机器人的参数对稳定性的影响。此外,在本文理论研究的基础上进行实际样机的验证是需要进一步研究的课题。
