T形截面轴压短柱畸变屈曲的无穷级数解与FEM验证
2023-02-02张文福郭雪妞杭昭明
张文福,郭雪妞,黄 斌,杭昭明
(1.安徽建筑大学 土木工程学院,安徽 合肥 230601;2.南京工程学院 建筑工程学院,江苏 南京 211167;3.东北石油大学 土木建筑工程学院,黑龙江 大庆 163318)
随着经济和新时期基础设施快速发展,建筑结构形式越来越复杂多变。钢管短柱轴心受压稳定性一直受到学者们的关注。历年来,学者们研究轴压柱的整体稳定性时,大多倾向于采用试验研究的方法。罗霞等[1]对7组高强钢管轴压柱进行了材料性能测试和加载试验,分析了不同长径比对轴压钢柱结构破坏形式的影响。程阿青等[2]通过对比加载试验,探究了膨胀剂掺量对自密实钢管试件延性和极限承载力的影响。有时试验法无法得到精确的结果,需要借助理论方法修正参数。韦建刚等[3]为研究高强钢管超高强混凝土柱的稳定性能,通过直接强度法修正现有规范中的系数,很好地预测了此类高强钢管超高性能混凝土柱的承载力和稳定性能。王珉[4]通过试验探究了在轴压下三肢钢管箱型截面柱的力学性能,用有限元分析研究了各类参数对结构极限承载力的影响。姚行友等[5]通过轴压试验研究了冷弯薄壁工字形截面柱畸变屈曲性能,基于试验结果以及有限元分析结果提出了直接强度法的修正公式,并验证其准确性和可行性。王群雄等[6]采用纤维模型法,基于4种不同本构关系组合模型模拟出构件的荷载与变形之间的关系,计算了中空钢管混凝土轴压柱的承载力。
相较于试验法和有限元分析法,关于轴压试验的研究成果较少,且关于轴压矩柱结构的畸变屈曲问题的研究多以试验以及经验公式为主,理论分析研究较少。因此,对短钢柱的弯扭屈曲及畸变屈曲问题的研究具有较高的科学价值。本文基于张文福[7]提出的“板-梁”理论与传统的能量法,对T形截面的畸变屈曲问题进行了理论研究及验证,旨在为提高轴压矩柱的稳定性提供理论依据。
1 理论计算模型
以T形截面柱为研究对象,引入2组符合右手螺旋法则的坐标系:全局xyz坐标系和局部nsz坐标系。选择截面的质心处作为全局坐标系的原点,选择每个板的质心处作为每个板的局部坐标系的原点。计算模型如图1所示。
2 畸变屈曲无穷级数解答
2.1 “板-梁”理论下T形截面构件的总势能方程
下翼缘平面内应变能为:
(1)
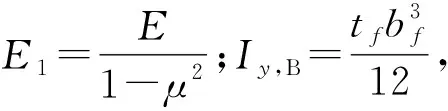
下翼缘平面外弯曲应变能为:
(2)

翼缘的总应变能为:
(3)
腹板的应变能为:

(4)

下翼缘的初应力势能为:
(5)
腹板的初应力势能为:
(6)
综上,T形截面构件的总势能为:

(7)
2.2 选用模态试函数
翼缘剪心的位移与转角的模态试函数为:
(8)
式(8)中,u为简支柱畸变屈曲时T形截面的侧向位移;φ为T形截面绕强迫转动轴转动时的扭转角;h为腹板上边缘到下翼缘形心线之间的距离;An和Bn均为无量纲的待定系数。
将式(8)代入式(7)中,可用Mathematica软件进行积分工作,得如下分项的结果。
(9)
(10)
(11)
(12)
式(11)~(12)中,P为z方向的力,即轴向压力;A为截面总面积;tB为翼缘厚度;tw为腹板厚度。轴压作用下的T形截面简支柱畸变屈曲的总势能可以表示为:
(13)
2.3 屈曲方程及解析解
根据势能驻值原理,先计算如下:
(14)
可得无穷阶无量纲屈曲方程:
(15)
其中{A}=[A1,A2,A3,…,An]T,{B}=[B1,B2,B3,…,Bn]T。为使{A},{B}不同时为0,必有:
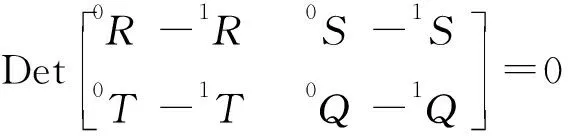
(16)
方程(15)的解为系数行列式结果取0时,T形截面简支柱受轴向压力而畸变屈曲时的临界屈曲荷载无穷级数解。由于傅里叶级数的收敛速度比较快,需要选取的项数并不多,可运用相应的Matlab程序进行大量参数分析。结果表明,此模态试函数的项数取5时,屈曲方程会趋向收敛,所得到的解满足精度的要求,即为临界屈曲荷载的精确解。
3 有限元验证
3.1 建立有限元模型
利用ANSYS有限元软件对T形截面短柱在轴力作用下的屈曲进行研究,并选用SHELL181单元对短柱进行模拟。
模拟的边界条件为两端简支,对模型上处于两端的所有节点施加轴向荷载。刚周边假设的模拟方法如图2所示。对T形截面构件的腹板进行畸变屈曲研究时,需要使用CERIG命令将翼缘截面上的所有节点耦合到翼缘中间的节点上,从而模拟对于翼缘的刚周边假设,如图2(a)所示。对整个T形截面进行弯扭屈曲研究时,需要将翼缘和腹板都施加刚周边,如图2(b)所示。

(a) 计算简图 (b) 计算断面图图1 计算模型

(a)畸变屈曲 (b) 弯扭屈曲图2 刚周边假设的模拟方法
在本研究中,在通用后处理的过程中,可以用命令流或GUI操作的形式得出屈曲荷载系数和屈曲模态。畸变屈曲形态图如图3所示。

(a)整体形态图 (b)断面图图3 畸变屈曲形态图
3.2 2种屈曲的界限问题
为了探究2种屈曲模式的过渡界限,研究了图2所示的2种模型的受力特性。2种模型在轴压时的临界荷载对比见表1。由表1可见,所求的2种屈曲的跨高比界限大约在6.67处,即在受轴向压力的情况下,当跨高比大于6.67时,柱子发生弯扭屈曲,当跨高比小于6.67时,开始由弯扭屈曲向畸变屈曲过渡。
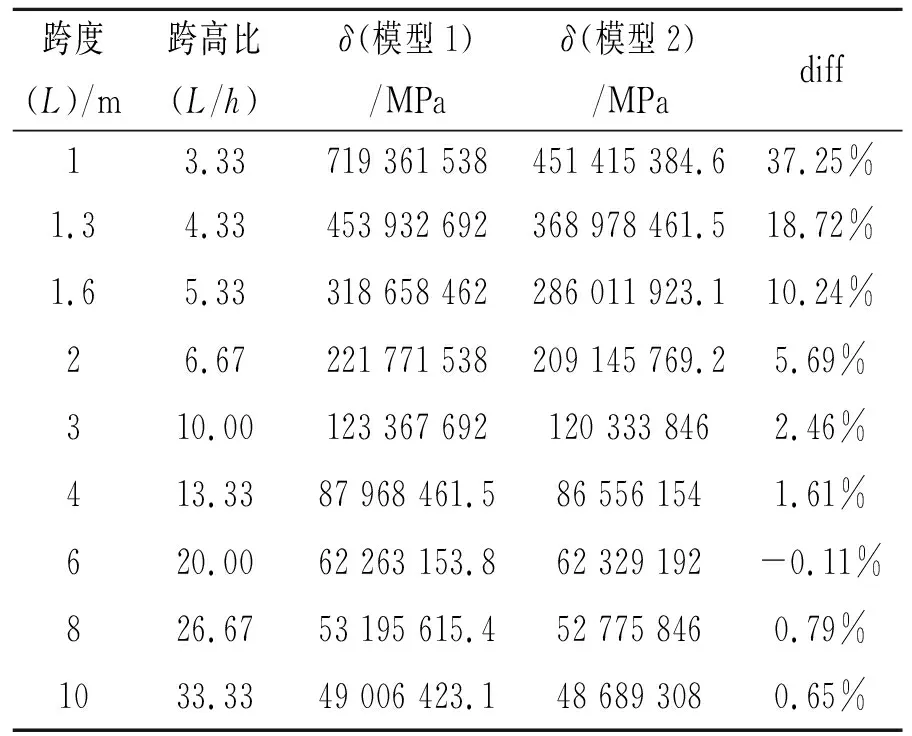
表1 2种模型在轴压时的临界荷载对比
3.3 理论与FEM误差分析
使用有限元模型分析所得的畸变屈曲临界荷载与“板-梁”理论计算所得的一阶、二阶及无穷阶结果对比见表2。从表2可以看出,跨高比在1.67~2.67之间时,以畸变屈曲为基础所做的有限元分析与理论计算的结果误差在10%以内,说明在这个范围内构件主要发生的是畸变屈曲。当跨高比大于2.67时,构件的屈曲形态从畸变屈曲逐渐向普通弯扭屈曲过渡。当跨高比小于1.67时,短柱已经过短,不容易发生屈曲,此时的破坏形态向多种复合模式转变。

表2 有限元结果与“板-梁”理论各阶结果对比
4 结论
1)在模拟轴压简支短柱发生屈曲时,跨高比的大小对于屈曲形式存在一定的影响。在短柱跨高比足够小,短柱足够短时,T形截面简支短柱在轴压荷载下的屈曲形式是明显的畸变屈曲。当跨高比大于6.67时,柱会发生弯扭屈曲;当跨高比小于6.67时,柱开始由弯扭屈曲向畸变屈曲过渡,即2种屈曲的跨高比界限大约在6.67处。
2)利用ANSYS有限元软件建模,在短柱端部施加轴压后,进行畸变屈曲性能的有限元分析,将FEM模拟解与推导的临界荷载理论解进行对比,吻合度较高,验证了理论解的正确性和推导公式的准确度,可对实际工程设计提供一定的参考。
