Computation Rate Maximization in Multi-User Cooperation-Assisted Wireless-Powered Mobile Edge Computing with OFDMA

Xinying Wu ,Yejun He,* ,Asad Saleem

1 College of Electronics and Information Engineering,Shenzhen University,Shenzhen 518060,China

2 Guangdong Engineering Research Center of Base Station Antennas and Propagation,Shenzhen Key Laboratory of Antennas and Propagation,Shenzhen 518060,China

Abstract: In the era of Internet of Things (IoT),mobile edge computing (MEC) and wireless power transfer (WPT) provide a prominent solution for computation-intensive applications to enhance computation capability and achieve sustainable energy supply.A wireless-powered mobile edge computing(WPMEC)system consisting of a hybrid access point(HAP)combined with MEC servers and many users is considered in this paper.In particular,a novel multiuser cooperation scheme based on orthogonal frequency division multiple access(OFDMA)is provided to improve the computation performance,where users can split the computation tasks into various parts for local computing,offloading to corresponding helper,and HAP for remote execution respectively with the aid of helper.Specifically,we aim at maximizing the weighted sum computation rate (WSCR) by optimizing time assignment,computation-task allocation,and transmission power at the same time while keeping energy neutrality in mind.We transform the original non-convex optimization problem to a convex optimization problem and then obtain a semi-closed form expression of the optimal solution by considering the convex optimization techniques.Simulation results demonstrate that the proposed multi-user cooperationassisted WPMEC scheme greatly improves the WSCR of all users than the existing schemes.In addition,OFDMA protocol increases the fairness and decreases delay among the users when compared to TDMA protocol.

Keywords: mobile edge computing (MEC);wireless power transfer (WPT);user cooperation;OFDMA;convex optimization

I.INTRODUCTION

In the new era of Internet of Things(IoT),a huge number of mobile devices play an increasingly important role in improving the quality of services such as virtual reality (VR),augmented reality (AR),smart grid and tele-surgery.However,these mobile devices with limited processing performance and battery capacity need to perform these latency-sensitive and computationintensive tasks[1].Fortunately,mobile edge computing (MEC) [2] can greatly improve the computation capability and latency performance of wireless devices by offloading computation tasks to the nearby MEC servers.In particular,the use of orthogonal frequency division multiple access (OFDMA) [3] provides a boost in computing performance when compared to standard time division multiple access(TDMA).

In addition,wireless power transfer(WPT)has been proposed as a means of ensuring a sustainable energy supply.In WPT-assisted MEC systems,the access point (AP) transmits radio frequency (RF) energy to multiple users over the downlink,afterwords wireless devices subsequently use energy harvesting (EH) to transform the received RF signals into power[4].The mobile devices can accomplish computation tasks by partial or full offloading to MEC servers and execute rest of the tasks locally with the harvested energy.In order to make full use of the advantages of MEC and WPT,many studies have adopted wireless-powered communication networks (WPCNs) to achieve selfsustainable computing for mobile devices.In WPCNs,a novel kind of hybrid AP (HAP) is deployed to not only charge wireless devices via wireless energy transfer (WET),but also assist MEC servers to execute users’offloading tasks.

Wireless-powered mobile edge computing system(WPMEC) in multiple users scenario has been investigated in a large number of studies.The research in[5] aimed to reduce HAP’s total energy usage while taking into account the users’specific computation delay constraints.In [6],the authors compared TDMA with non-orthogonal multiple access (NOMA) and formulated the energy efficiency maximization problem,where partial and binary offloading modes are considered respectively.As a result,NOMA protocol outperformed TDMA protocol with regard to energy efficiency.In a backscatter-assisted WPMEC based on OFDMA,the authors[3]investigated the optimization of the sum computation rate by concurrently optimizing the transmit power at the WET,system time allocation,backscatter coefficient,and offloading decisions of users.

In WPCNs,there exists a double near-far effect[7].When compared to users in the center of the cell,users near the edge of the cell not only harvest less energy from the HAP,but also they are required to transfer more power to reach the same rate [8].As a result,substantial unfairness arises between the users.To address unfairness,user cooperation (UC) can be considered as an efficient approach to improve computation capacity[9]and assure user fairness by allowing nearby users to function as a relay to carry the signal of distant users.

In wireless networks,user collaboration has been thoroughly explored in order to increase users’ transmission rates and communication reliability.A basic UC scenario has been considered in [10],where due to the blocked communication link between one user and MEC servers,the user needs to transfer offloading tasks to MEC servers with the aid of another user.Afterwards,they optimize the computation rate of the users by jointly optimizing the transmit power of energy node,the system time allocation,task allocation,and central processing unit(CPU)frequency of each user.The UC and NOMA for WPMEC system were jointly investigated in[11],where a multi-antenna HAP first broadcasts wireless energy to charge multiple single-antenna users.Then,by using the NOMA protocol,all the mobile users can offload tasks to the MEC servers at the same time.[12]investigated a WPMEC system based on NOMA consisting of two users,where the authors maximized the computation rate of the near user under the condition of the necessary computation rate requirement of the far user.In[13],a unique FDMA-based user cooperation model was proposed to increase the computing performance of active devices with one active user and several helpers.The authors maximized the computation rate of the active user by Lagrange duality method.In[8],the HAP and multiple cooperative fogs based on TDMA were investigated which minimize the energy consumption of the whole system by leveraging Lagrangian method.However,the TDMA protocol results in an additional delay for later users in multi-user systems.

In light of the above mentioned shortcomings,we investigate the multi-user cooperation-assisted WPMEC based on OFDMA,which consists of a HAP and numerous cooperative fogs.In addition,each cooperative fog contains a source node (active user) and a helper (idle user).Convex optimization techniques[14] are used to achieve an optimum solution of this problem in a semi-closed form.In comparison to existing methods,the simulation results demonstrate that the proposed scheme greatly enhances the WSCR of all source nodes.So the proposed scheme is more suitable for computing-intensive and latency-sensitive IoT devices in bad channel conditions.Our main contributions of this paper are as follows.

1)A novel design framework with UC and OFDMA is proposed to improve the computation performance of edge-cell users in the multi-user WPMEC system.We aim at maximizing the WSCR by optimizing time assignment,computation-task allocation,and transmission power at the same time while keeping energy neutrality in mind[15].

2)By using the variable substitution and convex optimization techniques,we transform the original nonconvex problem to a convex optimization problem and obtain a semi-closed form of this optimal solution.

3) The proposed multi-user cooperation-assisted WPMEC scheme greatly improves the WSCR of all users than the existing schemes.Furthermore,as compared to the TDMA protocol,the OFDMA protocol improves fairness and reduces user delay.

The remainder of this paper is organized as follows.Section II introduces the system model of multi-user cooperation-assisted WPMEC with OFDMA,including communication model,UC protocol,and computation model.Section III presents the computation rate maximization problem and the optimal solution.Simulation results are shown in Section IV,while Section V concludes this paper.

II.SYSTEM MODEL

2.1 Communication Model

In this paper,we consider a multi-user WPMEC system,including a HAP integrated MEC servers,andkcooperative fogs [8] denoted asK={1,2,...,K},each of them consists of a source node and a helper,as shown in Figure 1.The HAP withNantennas is considered to provide stable wireless energy supply and task offloading for 2ksingle-antenna users,where each user can convert the received signals into power for subsequent task execution.We suppose that there is a source node with a large number of tasks and a helper in an idle state for each cooperative fog.In addition,computation tasks can be arbitrarily divided into three parts and executed at source nodes,helpers,and MEC servers,respectively.In order to improve computation rate of source nodes,they may offload tasks to their corresponding helpers or HAP by UC from helpers.Part of the tasks may be completed by the helpers,while the other tasks can be offloaded to the HAP.The HAP delivers the computation result to the helpers after completing the tasks,and the helpers combine two halves of the computation results before returning them to their appropriate sourse nodes.

Figure 1. The multi-user cooperation-assisted WPMEC system.

2.2 Harvest-and-Offloading Protocol with UC and OFDMA

In order to avoid co-channel interference,we propose a multi-user cooperation-assisted harvest-and-offload protocol based on OFDMA,as shown in Figure 2.We maximize the WSCR of all source nodes within a time block,where the time block has a duration ofTseconds.In addition,each channel condition is quasi-static fading,which cannot change within a time block.In the first time slott0,the HAP provides wireless power to charge each user.During the subsequent time slotsT-t0,OFDMA can be used for task offloading and results downloading to avoid interference.

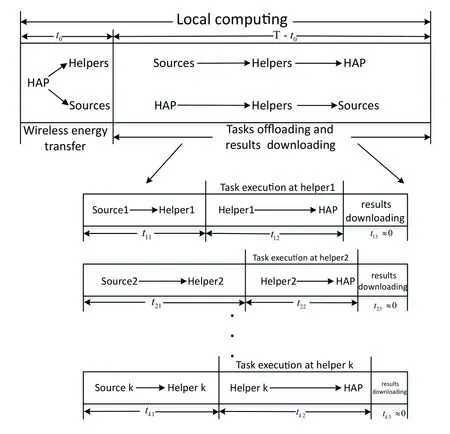
Figure 2. The harvest-and-offload protocol with UC and OFDMA.

2.3 Wireless Energy Transmission

In the first time slott0,HAP broadcasts wireless power to each user,therefore the harvested energy by eachsource node and helper can be defined as

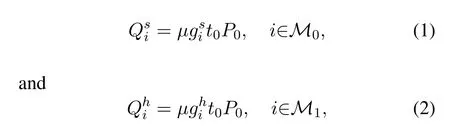
whereM0andM1represent the set of sourse nodes and the set of helpers respectively,0＜µ ＜1 represents energy conversion efficiency,denote the channel gain between thei-th sourse node and HAP,and between thei-th helper and HAP,respectively.P0is the constant transmit power of HAP.

With the harvested energy,the sourse nodes can split the computation tasks into three parts for local computing,offloading to helpers,and offloading to HAP for remote execution with the aid of corresponding helpers,respectively.We defineas the number of tasks performed by thei-th sourse node locally,its corresponding helper,and the remote HAP,respectively.

2.4 Computation Model

2.4.1 Local Computing Phase The number of tasks by local computing of thei-th sourse node is denoted as,wherei∈M0.Letϕs ＞0 represent the number of CPU cycles required to calculate 1 bit at the source nodes.In addition,the local CPU frequency of each sourse node can be expressed as(cycles per second).So the number of tasks by local computing of thei-th sourse node can be expressed as

whereis the local computation time.It is worth noting that the sourse nodes can execute tasks locally during the entire time block under the condition of enough energy supply.In addition,the corresponding local computation energy consumption is related to the local CPU frequencyand local computation time,so we define local computation energy consumption as

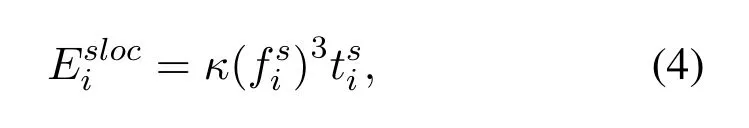
whereκrepresents the effective capacitance coefficient,which relays on the chipset structure of each sourse node.

2.4.2 Offloading to Helpers Phase

In addition to local computation,the sourse nodes can offload thebit tasks to corresponding helpers during theti1time period.During the subsequentti2period,the helpers can offload thebit data to HAP for remote execution and the remainingbit data is executed at the helpers.Thus,the number of tasks executed at thei-th helper can be expressed as

The corresponding computation consumption ati-th helper can be written as

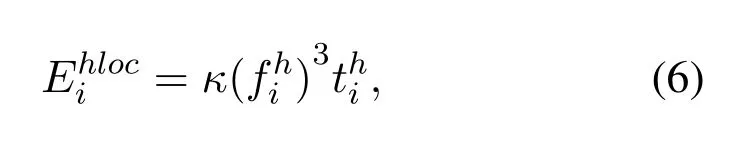
Lethiirepresent the channel gain between thei-th sourse node and thei-th helper node.Brepresents the network bandwidth allocated to each cooperative fog by this WPMEC system.Therefore,the channel capacity between thei-th sourse node and thei-th helper is defined as

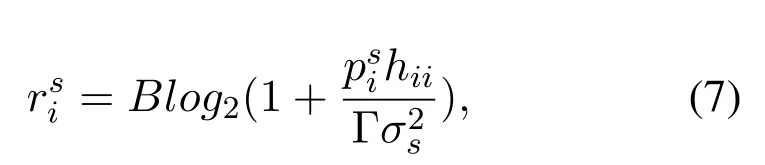
whererepresents the transmit power ofi-th sourse node,represents the noise power of the channel,and Γ is the proportion of additional noise generated by the modulation and coding scheme.So the maximum computation tasks transmitted between thei-th sourse node and thei-th helper are given by

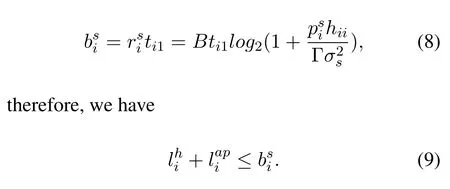
During this phase,the transmission energy consumption of thei-th sourse node is expressed as

2.4.3 Offloading to HAP Phase During theti2time period,thei-th helper can offload thelapibit tasks to the HAP.Heremeans the channel gain between thei-th helper and the HAP.Therefore,the channel capacity between thei-th helper and the HAP is given by

whererepresents the transmit power ofi-th sourse node,represents the noise power of the channel.The maximum computation tasks transmitted between thei-th sourse node and the HAP are expressed as

During this phase,the transmission energy consumption of thei-th helper is given by

What’s more,we notice that the energy of each source node and helper is supplied by the WET from the HAP.As a result,the energy neutrality constraints[13] are applied to all source nodes and helpers,i.e.,the total energy consumption of each user cannot exceed the total harvested energy over the same time block.So we have

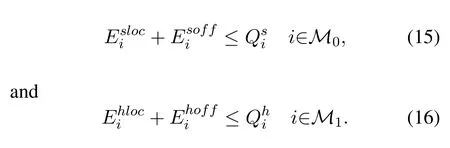
III.PROBLEM FORMULATION AND THE OPTIMAL SOLUTION

3.1 Problem Formulation

In this paper,we aim to maximize the WSCR of all sourse nodes by jointly optimizing the power allocation,the system time allocation,and resource allocation strategy.Mathematically,the WSCR can be formulated as

whereandω={ω1,ω2,...,ωk}represents the weight of.C1 and C2 represent the upper bound of channel capacity,where C3 and C4 mean local computation time constraints for sourse nodes and helpers,respectively.C5 and C6 demonstrate energy causal constraints,whereas C7 represents the time allocation limit of the whole system.C8 is the local computing constraint for sourse nodes and helpers,respectively.It is worth noting that due to the relationship of multivariate multiplication in C5 and C6 and non-convex constraints C1 and C2,the problem(P1)is considered as a non-convex optimization problem.Therefore,P1 cannot be solved by using directly the convex optimization algorithm.We turn P1 into a convex optimization problem and then find the optimal solution in the next subsection 3.2.

3.2 Problem Transformation

First of all,we introduce auxiliary variablesτiandϵi,where

with (18) and (19),the problem (P1) can be equivalently transformed into problem(P2)

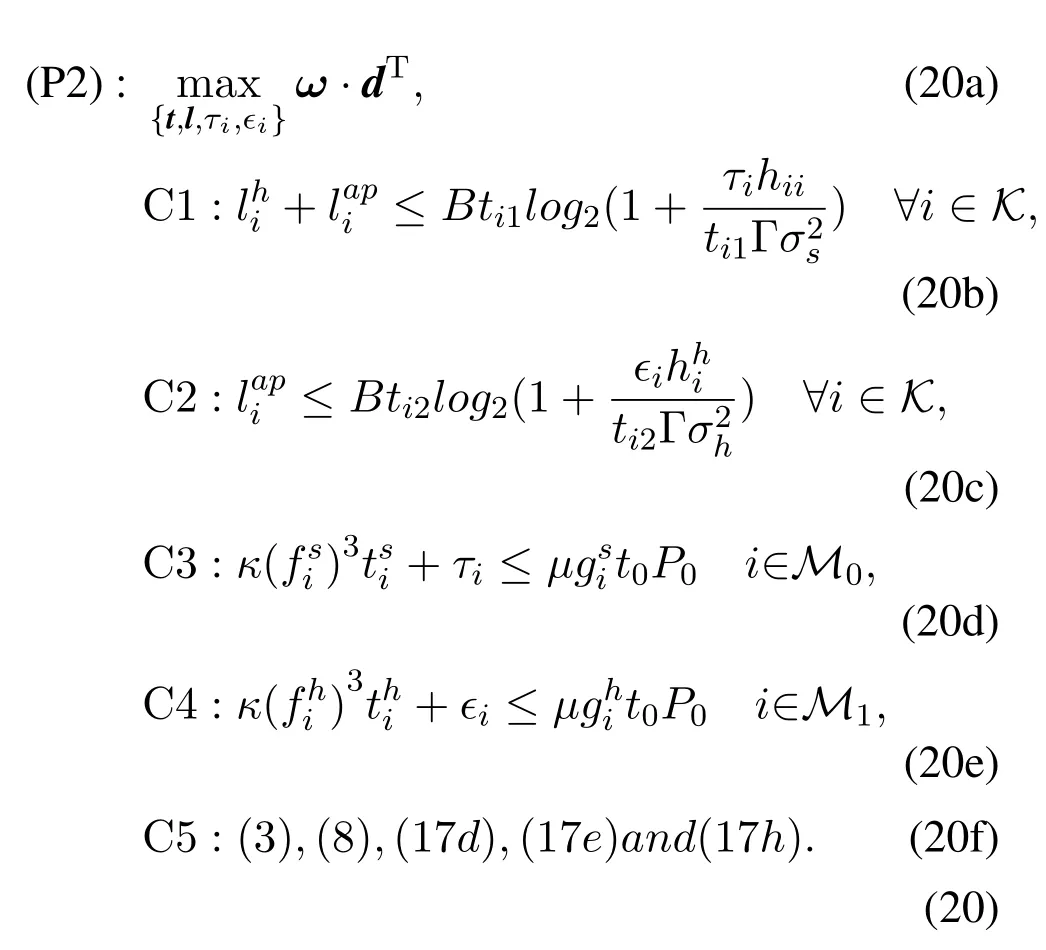
Lemma 1.The problem (P2) is a convex optimization problem,so we can effciently solve it by using the standard convex optimization tools[16].

Proof.See Appendix A.

3.3 Obtain Optimal Solution by Solving Problem(P2)

With Lemma 1,we may deduce from Lemma 1 that the problem(P2)is convex.Nevertheless,in order to gain essential engineering insights,we can obtain the optimal solution of problem(P2)by employing the Lagrange duality method in this subsection 3.3.First of all,we transform the problem (P2) into the problem(P3) by using (17i) to simplify the expression of the Lagrangian function.Thus,P2 can be equivalently expressed as

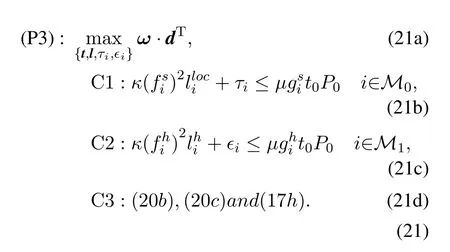
To solve problem (P3),we introduce the following theorems.

Theorem 1.In the multi-user cooperation-assisted WPMEC system with OFDMA,the optimal offloadingoffloading power of the i-th helper for maximizingthe computation rates of all source nodes have the following mathematical expressions.

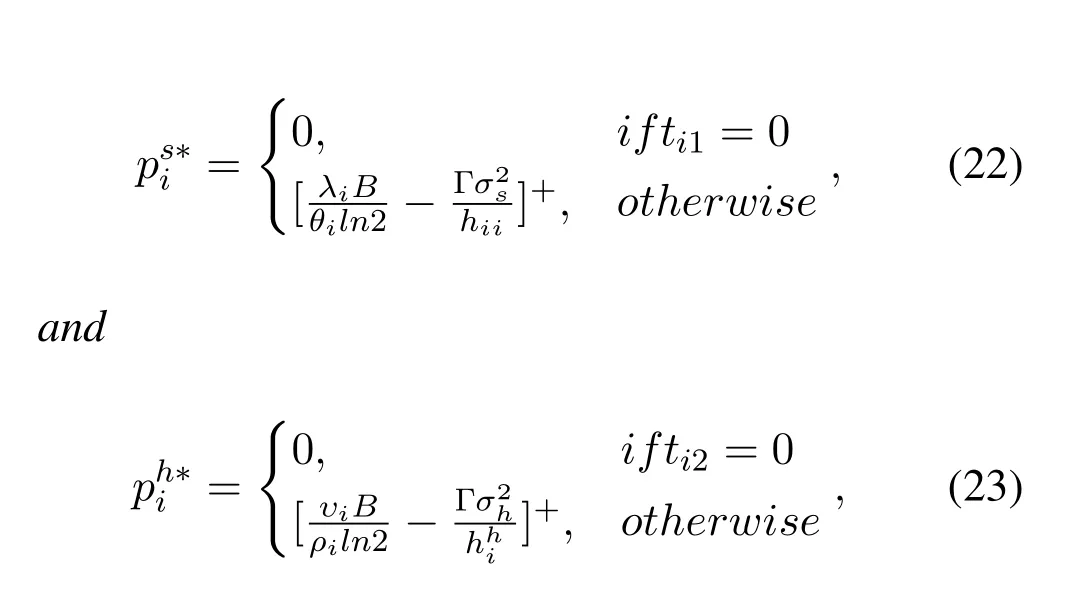
where we defne[x]+≜max{0,x}.Proof.See Appendix B.

We can see from Theorem 1,whenIn addition,whenIn other words,when the better channel conditions are provided,users are more willing to offload tasks.

By solving problem(P3),Theorem 2 is proposed to clarify the characteristic of the WET timet0.

Theorem 2.For these given θi,ρi and ψi,the optimal WET time needs to satisfy the following equation.

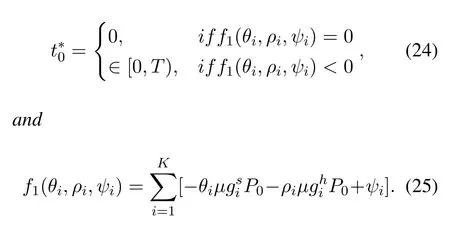
Proof.See Appendix C.

For the offloading time allocation sub-problem,the Lagrangian is a convex function aboutti1andti2,respectively.Thus there exist a pair of unique valuesti1andti2,which can maximize the computation rate.Let’s define the derivation of the Lagrangian with respect toti1andti2asf2(ti1)andf3(ti2),respectively.

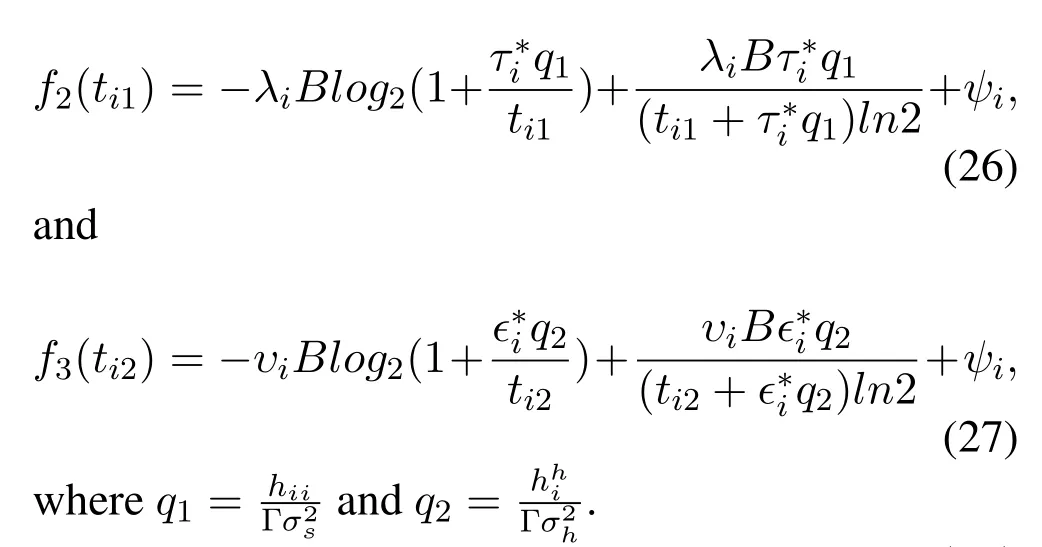
The maximizer is achieved at the roots off2(ti1)andf3(ti2),i.e.,f2(ti1)=0 andf3(ti2)=0.The bisection approach[14]can be used to retrieve the roots even if they are not solved in a closed form.

Now we obtain the optimal values ofpandt,then thecan be obtained form(3)and(8),respectively,whilecan be obtained form(17c).The pseudo code for solving problem (P1) is summarized in Algorithm 1.

IV.SIMULATION RESULTS

In this part,numerical results are provided and compared with the following four benchmark schemes to evaluate the computation performance of the proposed multi-user cooperation-assisted wireless-powered mobile edge computing design.

1.Only local computing:

In this scheme,all the source nodesi ∈M0exert computation tasks only by local computing.And offloading to helpers and HAP are not allowed,so we can set,∀i ∈M0.

2.With user cooperation based on TDMA:In a time blockT,the HAP first provides stable wireless energy supply for users,and then users can utilize the harvested energy for task execution with the help of the cooperative fog one by one[8].During the offloading process,users can use the bandwidth of the whole system,but the later users will face additional delays due to the time sequence,resulting in an unfairness of the system.

3.Without user cooperation based on OFDMA:Each source nodei ∈M0accomplishes its computation tasks only by local computing and directly offloading to HAP,without the aid of the helpers.In this scheme,each source node can offload its computation tasks simultaneously by OFDMA.

4.Without user cooperation based on TDMA:Each source nodei ∈M0accomplishes its computation tasks only by local computing and directly offloading to HAP,without the aid of the helpers.In this scheme,each source node can offload its computation tasks one by one based on TDMA.

In multi-user cooperation-assisted WPMEC,users with TDMA protocol can use the bandwidth of the whole system.In order to avoid interference,the time block in TDMA protocol has to be divided into various time slots where each time slot is corresponding to one user,thus there is a waiting delay for each user.The later user will face additional delays due to the time sequence,resulting in an unfairness of the system.Compared with TDMA protocol,users with OFDMA protocol can offload tasks at the same time by using orthogonal frequency band,which ensures fairness among users.As shown in Figure 3 to Figure 7,the scheme with OFDMA can achieve best WSCR in multi-user cooperation-assisted WPMEC system.

In these simulations,different from the classic 3-cooperative fog scenario in [8],the number of antennas at the HAP and the number of cooperative fogs are given by N=10 and K=5,respectively,which refers that there are 5 source nodes and 5 helpers in this simulation.Without the loss of generality,we adoptd-αas the path loss model,wheredrepresents the distance between different devices,αdenotes the path loss exponent.In addition,we considerThe details for other parameters are shown in Table 1.

Table 1. Simulation parameters.

Figure 3 illustrates the WSCR versus the distances between source nodes and HAP.As illustrated,the WSCR decreases as the distances between source nodes and HAP increase in all schemes.This is due to the fact that with less energy,the source nodes have to consume more energy to offload their computation tasks to HAP in without-user-cooperation schemes.However in user-cooperation schemes,the source nodes can offload computation tasks indirectly to HAP with the aid of helpers.As a result,without-usercooperation schemes decrease dramatically,whereas with-user-cooperation systems decrease lightly.In addition,when the distances between source nodes and HAP are large,the proposed user-cooperation with OFDMA scheme is able to achieve maximum computation rate than the other benchmark schemes.

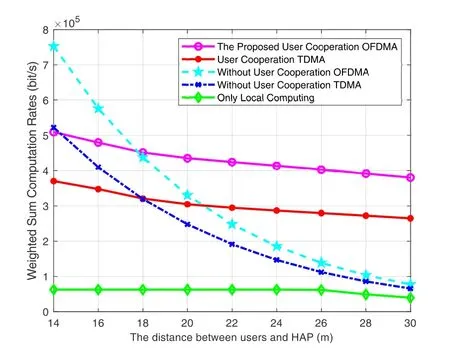
Figure 3. Weighted sum computation rates versus the distances between source nodes and HAP.

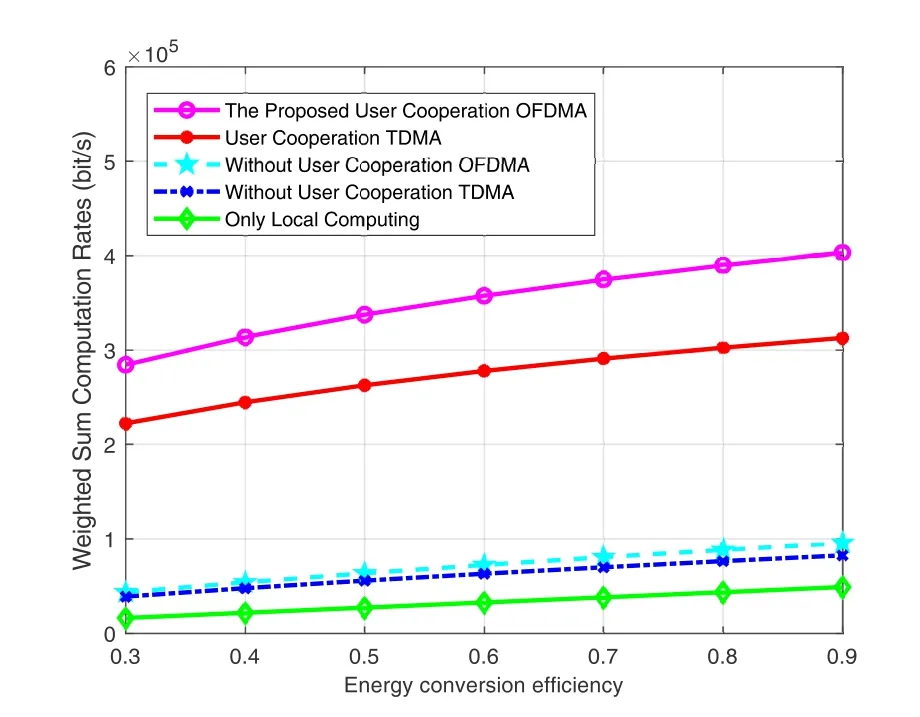
Figure 4. Weighted sum computation rates versus the energy conversion effciency.

Figure 4 shows the WSCR versus the energy conversion efficiency.As shown in Figure 4,the WSCR monotonically increases with the energy conversion efficiencyµfor all the five schemes.It is obvious that all source nodes and helpers can harvest much energy to compute or offload computation tasks.In addition,the performance of the proposed user-cooperation with OFDMA scheme achieves the best system performance among all schemes.The user-cooperation with TDMA scheme achieves the second best system performance.Furthermore,all user-cooperation designs outperform all non-user-cooperation designs and the only-local-computing design.In Figure 5,the relationship between the WSCR and the time block is presented.As desired,the WSCR for all schemes increases as the time blockTincreases.

When comparing the WSCR curve of the power ofWET in different scenarios based on OFDMA,it is clear that the WSCR grows as the power of WET in all schemes,owing to the large amount of energy is harvested as shown in Figure 6.Furthermore,these without-user-cooperation schemes outperform usercooperation schemes when the path loss exponent isα=2.6 while these user-cooperation schemes outperform these without-user-cooperation schemes whenα=3.5.The rationale for this is that under better channel conditions,it is appropriate to immediately offload compute tasks to HAP.However in bad channel conditions,the user cooperation technique should be used.

Figure 5. Weighted sum computation rates versus the time block.

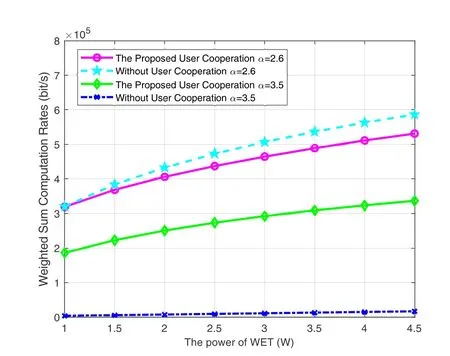
Figure 6. Weighted sum computation rates in different scenarios.

Figure 7. Weighted sum computation rates versus the path loss exponent.

In Figure 7,the impact of the path loss exponentαbetween source nodes and HAP on the performance of the maximum WSCR is shown.It is obvious that these user-cooperation schemes outperform the without-user-cooperation scheme and the OFDMA scheme outperforms the TDMA scheme with user cooperation when largeαvalues are considered.In addition,for the only-local-computing scheme,whenα ≥3.1,the harvested energy is not sufficient for local computing during the entire time slotT,so the WSCR decreases with the less local computing time.

V.CONCLUSION

In this paper,we investigated a novel multiuser cooperation-assisted WPMEC system based on OFDMA.The problem of maximizing the WSCR is formulated by jointly optimizing the transmit power of the users,computation-task allocation,and the system time allocation within a time block by considering the energy causality constraints.We proposed a multiuser cooperation-assisted harvest-and-offload protocol based on OFDMA,where the users first harvest the energy by WPT and then make full use of the energy to accomplish computation tasks locally or with the help of cooperative fogs and HAP.Based on the convex optimization techniques,we obtained the optimal solution in a semi-closed form and proposed a joint computation offloading and resource allocation algorithm.Simulation results show that the proposed scheme outperforms the existing schemes such as the user-cooperation design based on TDMA in maximizing the WSCR.Thus,the proposed scheme integrating WPT with MEC provides maximum WSCR and sustainable energy supply for IoT devices especially in bad channel conditions.

APPENDIX

A.Proof of Lemma 1

First of all,the objective function is linear and the constraints (17d),(17e),and (17h) are linear inequality constraints while (3) and (8) are linear equality constraints,so it is obvious that the objective function and the constraint C5 of problem (P2) satisfy the conditions of a convex optimization problem.In the constraint C1,is a linear function with regard toIn addition,is the perspective function of,which is a concave function with regard toτi.The perspective function preserves convexity of original function[16],sois concave function with regard toτiandti1.Therefore,by a simple algebraic transformation,we can prove that the constraint C1 is convex.For C3,the left sideis a linear function with regard toThe right sideis also a linear function with respect tot0.Thus,we can get that the constraint C3 is also convex.By exploiting the similar mathematical method for the constraints C2 and C4,we can easily prove that the constraints C2 and C4 are also convex constraints.Thus,it is proved that problem(P2)is convex.

B.Proof of Theorem 1

Letλi ≥0,υi ≥0,θi ≥0,ρi ≥0 andψi ≥0 denote the Lagrange multiplier associated with the constraints (20b),(20c),C1,C2 and (17h) in problem(P3),respectively.The Lagrangian function related to the problem(P3)is expressed as

With the Lagrangian function of problem (P3),the first-order optimality condition can be used to obtain the optimal solution.The gradients of the LagrangianLwith regard toτiandϵiare respectively expressed as

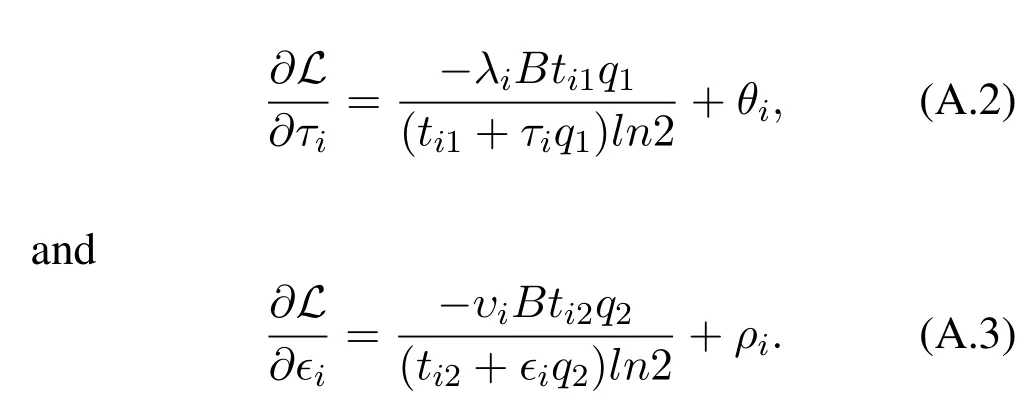
Let their gradients be zero.Thus,we have

C.Proof of Theorem 2

Letf1(θi,ρi,ψi)denote the gradient of the Lagrangian functionLwith regard tot0,and it can be expressed as

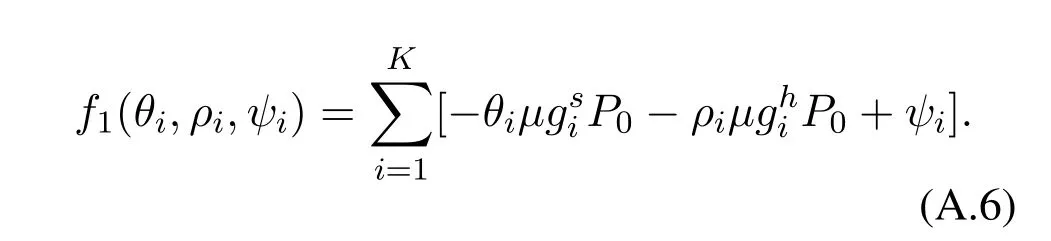
For the givenθi,ρi,ψi,we can obtain that the Lagrangian functionLis a linear function with respect tot0.Because problem(P3)is convex,the Slater’s conditions[16]are satisfied.And the Lagrangian functionLis upper-bounded with regard tot0.So it can be concluded asf1(θi,ρi,ψi)≤0.Whenf1(θi,ρi,ψi)＜0,the maximum Lagrangian functionLis obtained whent0=0.And whenf1(θi,ρi,ψi)=0,the Lagrangian functionLis constant value with regard tot0,sot0is an arbitrary value within[0,T].Thus,the proof for Theorem 2 is completed.

ACKNOWLEDGEMENT

This work is supported in part by the National Natural Science Foundation of China(NSFC)under Grant No.62071306,and in part by Shenzhen Science and Technology Program under Grants JCYJ202001091-13601723,JSGG20210802154203011 and JSGG-20210420091805014.