Joint Multi-Domain Channel Estimation Based on Sparse Bayesian Learning for OTFS System
2023-02-02YongLiaoXueLi
Yong Liao,Xue Li
School of Microelectronics and Communication Engineering,Chongqing University,Chongqing 400044,China
Abstract: Since orthogonal time-frequency space(OTFS) can effectively handle the problems caused by Doppler effect in high-mobility environment,it has gradually become a promising candidate for modulation scheme in the next generation of mobile communication.However,the inter-Doppler interference(IDI) problem caused by fractional Doppler poses great challenges to channel estimation.To avoid this problem,this paper proposes a joint time and delay-Doppler(DD)domain based on sparse Bayesian learning (SBL) channel estimation algorithm.Firstly,we derive the original channel response (OCR) from the time domain channel impulse response (CIR),which can reflect the channel variation during one OTFS symbol.Compare with the traditional channel model,the OCR can avoid the IDI problem.After that,the dimension of OCR is reduced by using the basis expansion model (BEM) and the relationship between the time and DD domain channel model,so that we have turned the underdetermined problem into an overdetermined problem.Finally,in terms of sparsity of channel in delay domain,SBL algorithm is used to estimate the basis coefficients in the BEM without any priori information of channel.The simulation results show the effectiveness and superiority of the proposed channel estimation algorithm.
Keywords: OTFS;sparse Bayesian learning;basis expansion model;channel estimation
I.INTRODUCTION
Wireless channels are mainly affected by multipath fading and Doppler,and different carrier modulation schemes also determine the transmission performance of the system.The existing modulation scheme adopts mainly orthogonal frequency division multiplexing(OFDM),in which the signal is modulated into multiple subcarriers for transmission in the channel,thus it can effectively improve multipath resistance.However,in a high-mobility scenario,the Doppler shift will seriously destroy the orthogonality of subcarriers,resulting in subcarrier interference and the performance bottleneck of the system[1,2].Due to its effective resistance,orthogonal time-frequency space(OTFS)has been proposed [3].OTFS is a two-dimensional (2D)modulation scheme,whose principle is to utilize the delay-Doppler(DD)domain to represent informationcarrying symbols,and then spread them to the entire time-frequency (TF) grid by inverse symplectic finite Fourier transform (ISFFT) operation [4,5].In this process,all data symbols transmitted in the doublyselective channel will be equally affected,thus OTFS modulation can achieve the diversity gain of the whole channel and reduce the performance loss[6,7].
Despite the above advantages of OTFS,the DD domain diffusion of OTFS symbols caused by the influence of 2D convolution of channel in the transmission process brings great challenges to pilot assignment and channel estimation.In [8],in order to mitigate the mutual interference between data and pilot,an impulse is inserted into the whole frame for channel estimation,and the estimated channel information is used for signal detection in the next frame.However,this method greatly reduces spectral efficiency,and when the channel varies too rapidly,the channel of the next frame is still outdated.Therefore,a guard interval is usually inserted around the pilot and data symbols to avoid interference between the pilot and data symbols.In[9],an impulse signal is taken as pilot,while some guard intervals are inserted around it.Finally,the channel response of DD domain is estimated by threshold method.However,this channel estimation method is sensitive to the guard interval,and the choice of threshold possibly affects the channel estimation performance.In fact,channel estimation methods based on compressed sensing have been proposed for DD domain channel estimation.For example,the author of [10] proposed a three-dimensional structured orthogonal matching pursuit(SOMP)algorithm by utilizing the channel sparsity in the delay domain,Doppler domain and angle domain.Furthermore,[11]also utilized the sparsity of these three dimensions and adopted three-dimensional Newtonian orthogonal matching pursuit (NOMP) to recover the channel parameters in the TF domain of the antenna,including channel gain,arrival direction,delay and Doppler frequency.In addition,the sparse Bayesian learning(SBL) was applied to OTFS channel estimation in[12],which proves that this method is superior to OMP algorithm.However,the method in [12] assumes that the path is known and only applies to integer Doppler,where all the estimated Doppler shift are located on the grid of DD domain.It greatly limits the application scenarios of channel estimation.
In the practical scenario,the Doppler frequency of the wireless channel is not fixed,but meets the change of the U-shaped Doppler spectrum [13].In the process,Doppler of each path cannot be accurately quantified to each grid,thus produces inter-Doppler interference (IDI).In order to solve the above problems,the original channel response (OCR) is derived from channel impulse response (CIR) in time domain,and the paper proposes joint time and DD domain channel model that can be used in practical application scenarios.Finally,a channel estimation method based on SBL is proposed to estimate the basis coefficients by taking advantage of the sparsity of the delay domain.The main contributions of this paper are summarized as follows:
(1)In this paper,channel can be estimated by joint time and the DD domain.Specifically,the OCR of the OTFS system is derived from the time domain.The channel response reflects the variation of channel within an OTFS symbol,thus avoiding the IDI.In addition,according to the relationship between the time domain and DD domain,the channel estimation problem is converted to the basis coefficients estimation(BCE)problem by employing the basis expansion model (BEM),and the underdetermined problem is transformed into an overdetermined problem.
(2) On the basis of the sparsity of channel in delay domain,we propose a BCE algorithm based on SBL.In this process,we let the channel path unknown,and the algorithm can still accurately estimate the number and location of the path,which greatly improves the performance of the receiver.
The structure of this paper is organized as follows.Section II describes the OTFS system model,including the OCR of DD domain.In Section III,on the basis of OCR,a joint multi-domain channel estimation model is derived by using the BEM and the relationship between time domain and DD domain channel.Meanwhile,SBL algorithm is used to estimate basis coefficients by using the sparsity of channel in the delay domain.In Section IV,the effectiveness of the proposed algorithm is verified by simulation,and the complexity of the algorithm is analyzed.Finally,the conclusion is summarized in Section V.
II.OTFS SYSTEM MODEL
According to the derivation of literature[14]and[15],it is known that the input-output relation of OTFS signal is two-dimensional convolution.We can defineY[n,m]to represent the[n,m]-th element on the grid of received signal in DD domain,wheren ∈[0,N-1],m ∈[0,M-1]andM,Nare the grid size of delay domain and Doppler domain respectively.Then,Y[n,m]can be expressed as
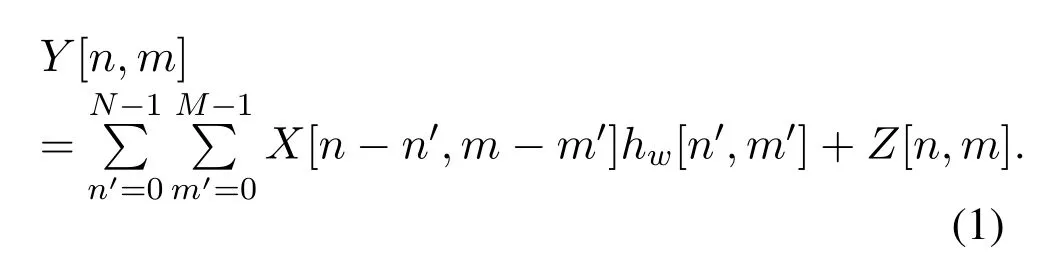
Note thatX[n-n′,m-m′]represents the[n-n′,mm′]-th element of transmitted signal grid in the DD domain,Z[n,m] denotes additive white Gaussian noise with zero mean and variance ofσ2.The discrete DD domain channel responsehw[n′,m′] is sampled from the real DD domain channel,which is defined as
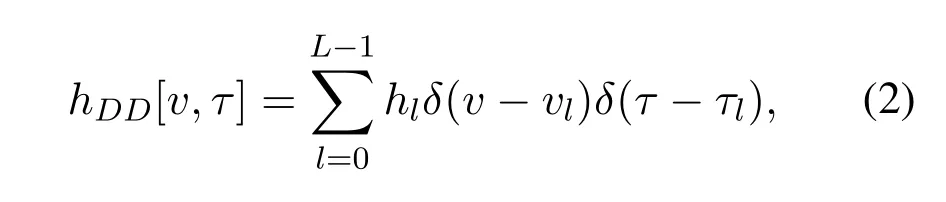
wherehl,vlandτldenote the complex attenuation coefficients,delay and Doppler frequency of thel-th path respectively,andδ(·) is Dirac Delta functions,whereLis the number of channel path and the delay-index of the DD planelchanges from 0 toL-1.Note that the maximum delay of a channel is not larger than the cyclic prefix(CP)length of the channel,i.e.L ≤NCP.However,in OTFS system,DD domain channel response needs to be quantified by resource grid,thus the discrete DD domain channel response is derived as
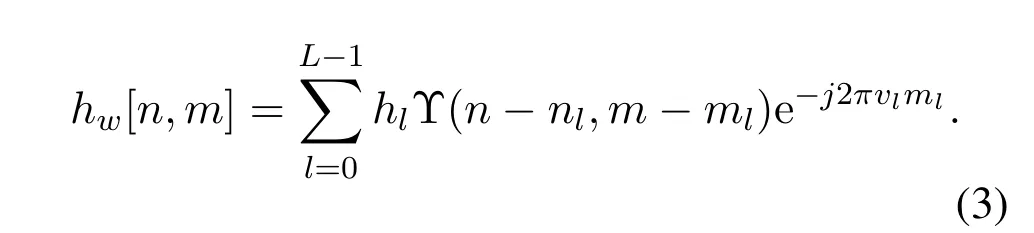
The tap of the Doppler and delay are generated bynl=vlNT,ml=τlMΔfrespectively,whereTand Δfrepresent the duration of an OTFS symbol and subcarrier interval.Define Υ(·)as the sampling function,we have
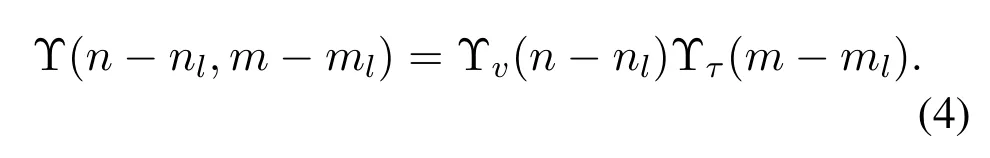
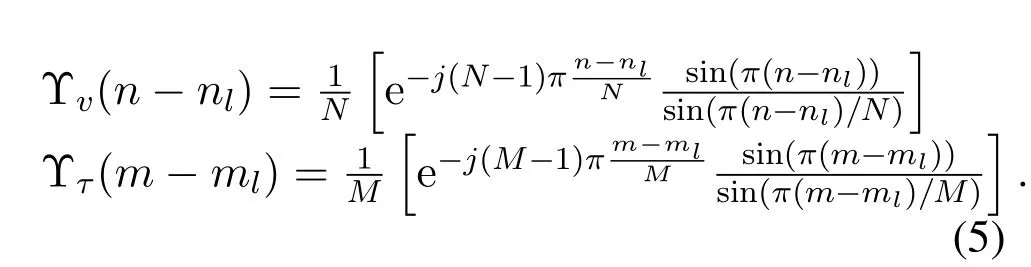
According to Eq.(4)and(5),sincemandnare integer,when the tap of the Dopplernland delaymlare fraction,the entry Υv(n-nl)and Υτ(m-ml)can produce IDI[16]and inter-symbol-interference(ISI)[17].Intuitively,fraction Doppler tap cannot ensure the true Doppler frequency located on specific grid points,then the energy of the tap will be scattered on other Doppler grid points,which is also called energy leakage.
From another point of view,in order to avoid the fractional Doppler caused by sampling,we can focus on the TF domain channel response,which is converted to the DD domain channel response by means of the symplectic Fourier transform(SFFT).However,the frequency domain channel response always assumes that the CIR is constant over the duration of a symbol[18].Figure 1 and 2 demonstrate the real channel and the effective channel assumed by frequency domain estimation in high-mobility scenario respectively.
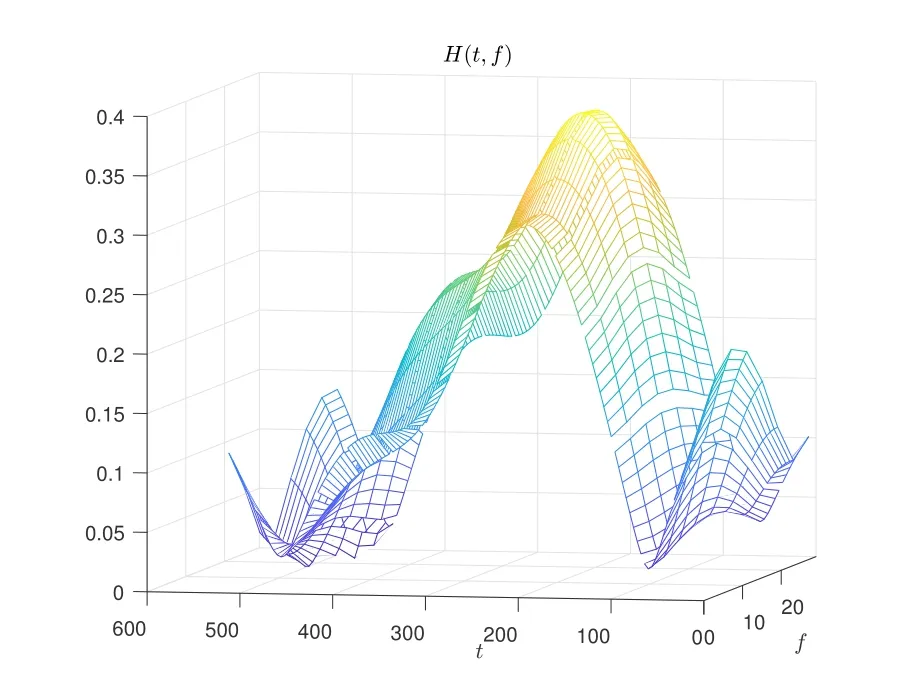
Figure 1. The real channel in high-mobility scenario.
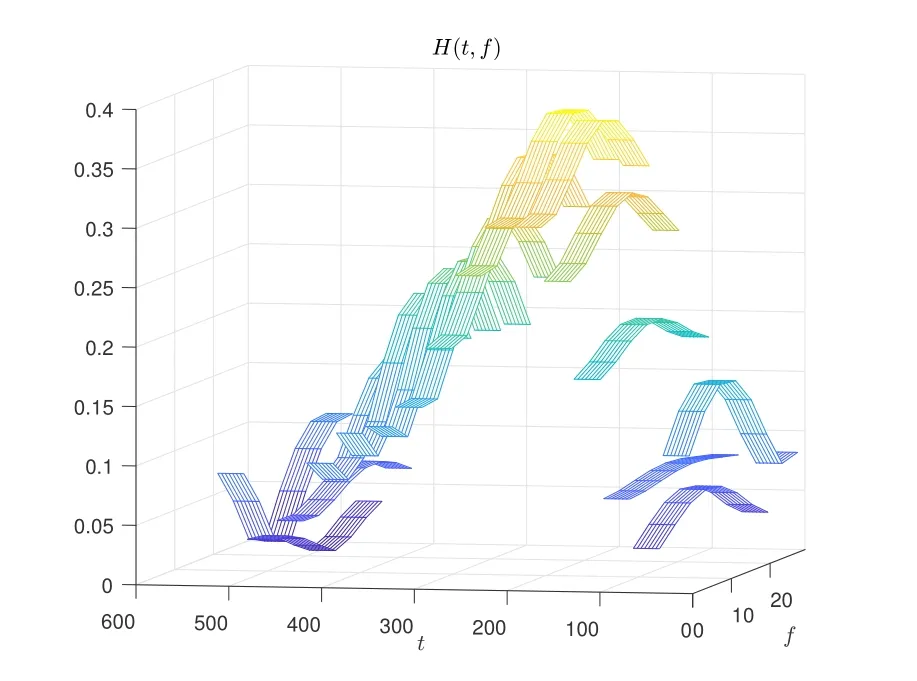
Figure 2. Frequency domain estimation channel in highmobility scenario.
It can be seen that there is modeling error in frequency domain channel response,which will also lead to corresponding interference in DD domain.Although there is no fractional Doppler problem at this time,the channel response still cannot be accurately obtained due to the existence of this interference.Accordingly,in order to mitigate this interference,we can obtain the OCR from the CIR,whose advantage is that the changes of each sampling point in the direction of the Doppler domain can be fully considered.Define H∈CMN×Las the OCR of the DD domain,wherem′ ∈[0,M -1]andn′ ∈[0,N -1]denote as sampling-points-index in the Doppler domain and the Doppler-index of the DD plane respectively.Figure 3 presents the OCR of thel0-th path.For ease of observing the changes of each sampling point in the Doppler domain,it is transformed into a grid form.
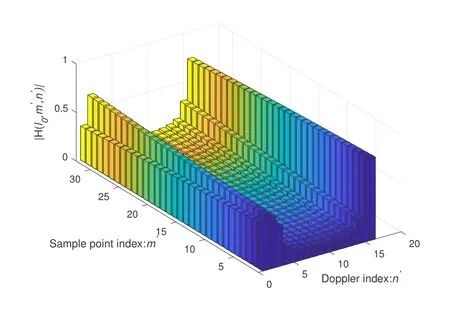
Figure 3. The magnitude of the OCR of the l0-th path.

Figure 4. The pilot and data symbol positions of transmitter.
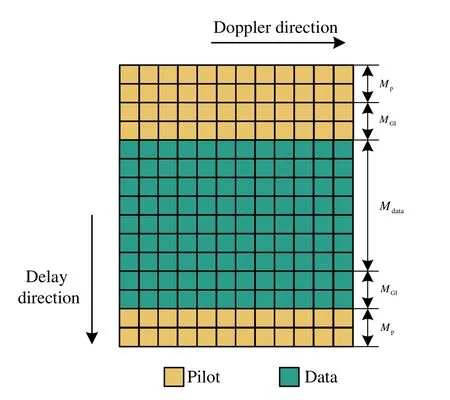
Figure 5. The pilot and data symbol positions of receiver.
It’s found that the sampling point of each Doppler index withm′varies rapidly from 0 toM -1.Therefore,the OCR can fully consider the variation of the different sampling point,which can solve the performance bottleneck.The relationship between CIR and OCR is given as
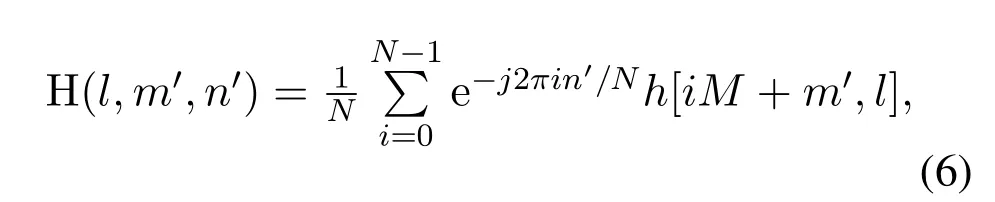
whereh[iM+m′,l]represents the(iM+m′)-th sampling point in thel-th tap of the CIR.Here,the output signal is rewritten as
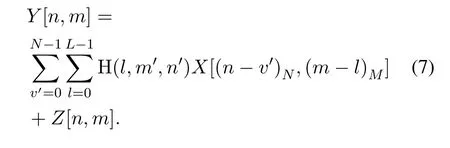
III.SBL-BASED BASIS COEFFICIRNTS CHANNEL ESTIMATION
This section aims to describe the channel estimation algorithm.According to the characteristics of the OCR described above,we employ BEM to reduce its dimension,so as to transform the channel estimation problem into a BCE problem.In terms of this problem,a BCE algorithm based on SBL is proposed.
3.1 Joint Multi-Domain Channel Estimation Model
As the channel estimation algorithm assumes that the path is unknown in this paper,letL=NCPin the following text.The convolution relation of Eq.(7) is rewritten into the matrix relation as follows:
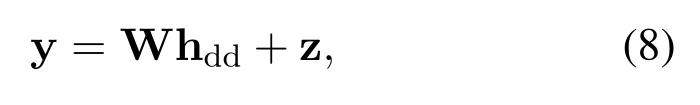
where y=vec(YT)∈CMN×1,hdd=vec(H)∈CMNL×1and z∈CMN×1denote the received symbol vector of DD domain,the OCR vector and noise vector respectively;W=[W0,...,Wl,...,WL-1]∈CMN×MNLis composed of the transmission symbol of DD domain,where Wl ∈CMN×MNis a block diagonal matrix containingMsmall matrix ofN ×Ndimension,expressed as Δi,i ∈[1,M].Define a new indexrl=circshift(1 :M,l)=(M,M -1,...,M -l+1,1,2,...,M -l)∈C1×Mand let,we have

It can be seen from Eq.(8) that the dimension of hddis larger than y,which indicates that the equation is an underdetermined equation and cannot be solved directly.In order to estimate hdd,we adopt BEM to reduce the dimension of hdd,whose main idea is to use a set of basis vector and corresponding basis coefficients to represent each path tap [19].According to Eq.(6),the OCR of thel-th path Hlis related to the CIR hl.Therefore,the BEM is used to reduce the dimension of hl,and then the basis vector of hlis transformed into DD domain through the relation of Eq.(6).Finally,the basis matrix of DD domain is further obtained.Express thel-th path of the CIR as follows:
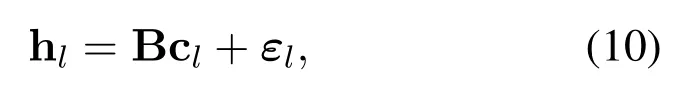
where the basis matrix B=[b0,b1,···,bQ-1]∈CMN×Qin the time domain consists of the basis vector bq ∈CMN×1.cl ∈CQis basis coefficient andεl ∈CNis the modeling error vector.To improve the modeling performance,this paper adopts the commonly used discrete prolate Spheroidal basis expansion model(DPS-BEM)as the basis matrix[20].Joint time and DD domain channel,i.e.Eq.(6)and(10),Hlis derived as
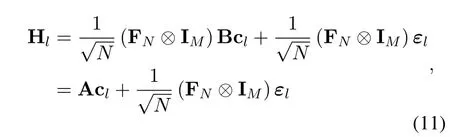
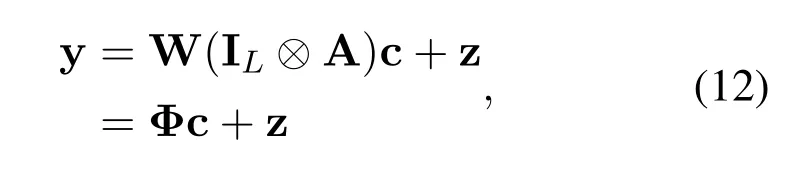
where c=[c0,...,cl,...,cL-1]T∈CQLand ΦW(IL ⊗A)∈CMN×QL.To estimate the OCR,pilot sequences need to be inserted at the transmitter.We design a specific pattern shown in Figure 4.In the figure,the OTFS frame of size isM ×N.The yellow part represents pilot symbol,and the green part represents data symbol,namely,MpandMGIdetermine the transmission efficiency of frame structure.In the delay direction,in order to mitigate the interference between pilot and data,a guard intervalMGI,i.e.the white part in Figure 4 is inserted around the pilot structure.Note thatMGIdepends on the delay of channel.Since the transmitted signal that experience the fading channel can cause the diffusion between different symbols,the yellow part is used for channel estimation and the green part for signal detection in Figure 5.
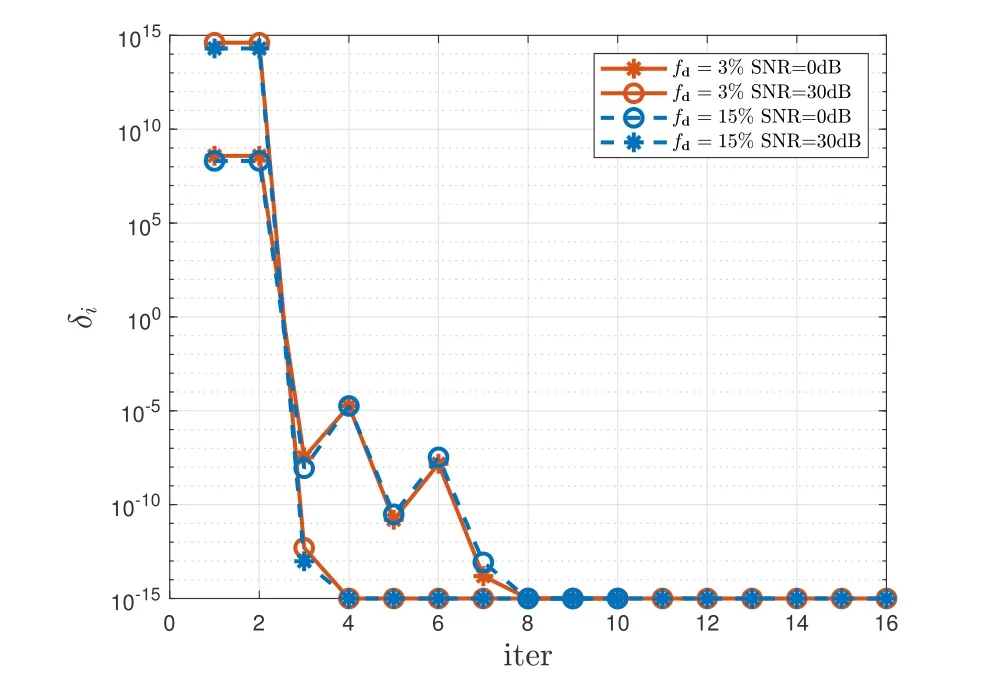
Figure 6. Convergence process of SBL algorithm,fd=3%and 15%respectively,SNR=0dB and 30dB respectively.
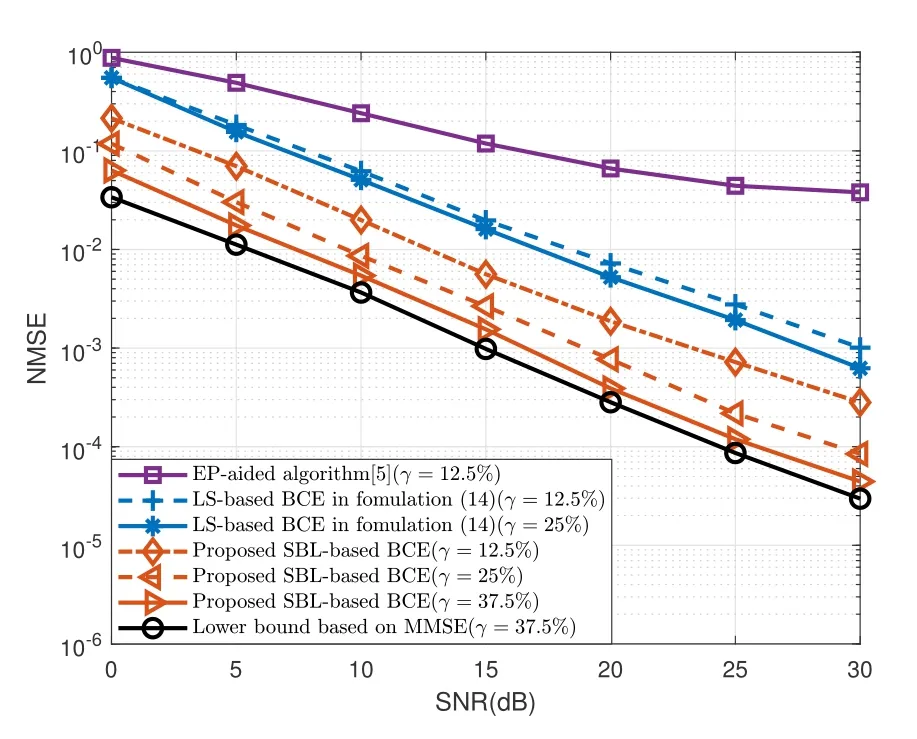
Figure 7. The NMSE performance with velocities of 137 km/h,i.e.fd=3%.
To estimate the OCR,we can multiply a matrix to take the pilot position,and Eq.(12)is converted to
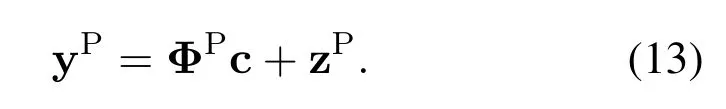
Generally,QsatisfiesQ < MN/L.Therefore,Eq.(13) is an overdetermined equation,hence least squares (LS) and minimum mean square error(MMSE) algorithms can be directly used to estimate the basis coefficients.
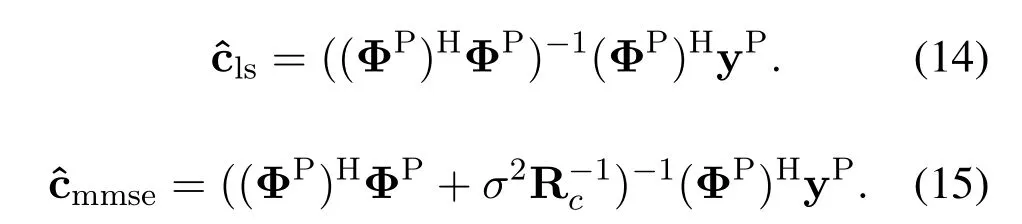
In Eq.(15),the covariance matrix of c is Rc=blkdiag{Rc0,...,Rcl,...,RcL-1} ∈CQL×QL,
where Rcl=B-1Rhl(B-1)Hand Rhlis the covariance matrix of Rhl.However,the BCE algorithm based on LS,called LS-based BCE for simplicity,ignores the influence of noise,which limits the performance.And the algorithm based on MMSE requires the prior information of the covariance matrix of the basis coefficients,thus it’s impractical and used as the lower bound of the channel estimation performance in the following simulation.In fact,the number of the pathLis far less than CP lengthNCP,thus onlyLtap coefficients exist large values,and the rest tap coefficients are small enough to be ignored [21],which shows the basis coefficients are sparse.Taking advantage of this property,the SBL algorithm can be employed to estimate the basis coefficients of the channel,which will be described in detail in Section 3.2.
3.2 Sparse Bayesian Learning Algorithm
For OTFS systems,based on Eq.(13),we assume that the Gaussian noise vector zPsatisfiesN(0,σ2I).Hence,the likelihood function of the received signal y satisfiesN(ΦPc,σ2I).In the SBL framework,the key of the SBL algorithm is to make prior assumptions about estimated parameters c,which is equivalent to regularization[22]:
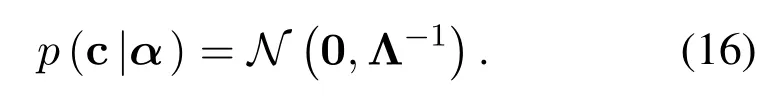
Particularly,Λ=diag{α(1),α(2),...,α(J)} ∈CJ×J,α ∈CJ.α(j) denotes the hyperparameter controlling thej-th term ofc(j),asα(j)→ ∞,c(j)→0.Therefore,the estimate ofαis critical.However,it is difficult to obtain the hyperparametersα,thus the method of hierarchical priors is adopted to define the prior of the hyperparameters to obey the gamma distribution [23].Similarity,assume that the noise varianceσ-2also obeys the gamma distribution.According to the Bayesian formula,it can be seen that the posterior probability of c satisfies Gaussian distribution:
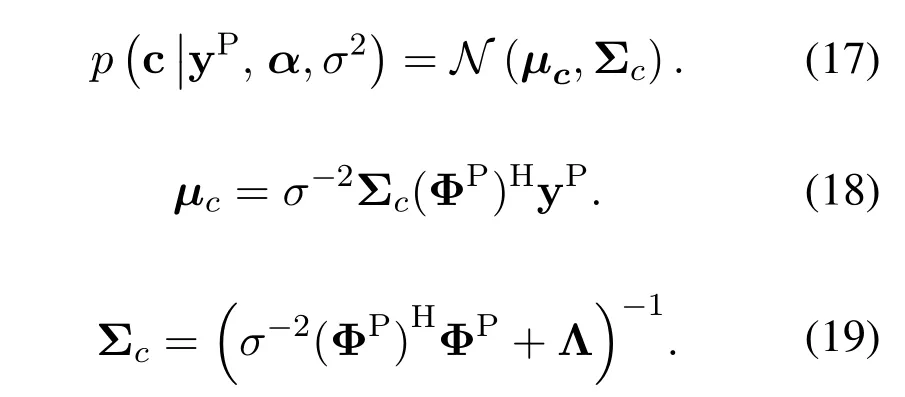
The unknown parametersα,σ2can be obtained by means of Type-II maximum likelihood algorithm[24].The update rules are as follows:
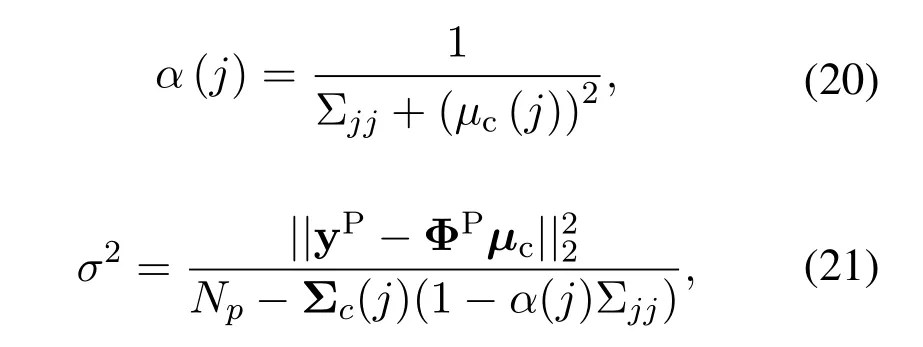
whereNprepresents the number of the pilot,Σjjrepresentsj-th diagonal element of Σc.The process of BCE algorithm based on the SBL learning includes initialization and iteration.
Initialization: For the sake of representation,let=α-1,β=σ2and set(0)=0,β=1.(·)(i)denotesi-th iteration.According to Eq.(18)and(19),can be directly calculated.
Iteration: The update formula of(i)is given as
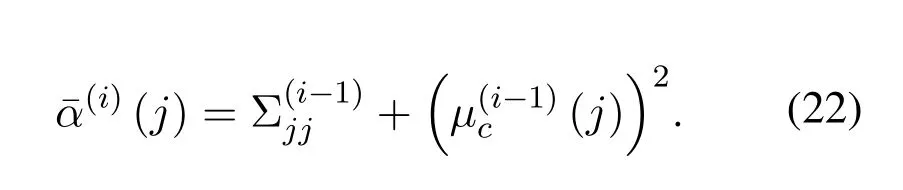
Subsequently,update the noise estimation:

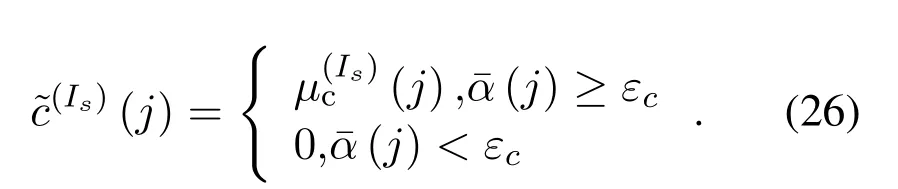

Specifically,the iteration process is summarized in Algorithm 1.
IV.COMPLEXITY AND SIMULATION ANALYSIS
4.1 Complexity Analysis
For LS-based BCE,the pseudo-inverse matrix of ΦPneed to be computed,thus its computational complexity is(QL)2MN+(QL)3+(QL)MN+(QL)2.
The BCE algorithm formula based on MMSE criterion is shown in Eq.(15),where the complexity of matrix Rcinversion is added,hence the complexity is(QL)2MN+2(QL)3+(QL)MN+(QL)2.
Finally,the BCE algorithm based on SBL is analyzed,whose computational complexity is dominated by mean,variance and noise update,i.e.Is[(QL)2MN+(QL)3+(QL)2+2(QL)MN+MN+QL].The complexity of different schemes are summarize in Table 1.Compared with the algorithms above,we can observe that this computational complexity depends onIs.Figure 6 shows that in the convergence process of SBL algorithm,the variation of norm of parameter updatewith the number of iterations,wherefdis 3%and 15%respectively,SNR is 0 dB and 30 dB respectively.It’s found that SBL algorithm can achieve the fast convergence with less than 10 times.In terms of complexity,the multiples here do not increase the complexity by orders of magnitude.Meanwhile,SBL can be solved directly without any prior information.Therefore,compared with the above algorithms,the complexity of SBL algorithm is acceptable.

Table 1. The complexity of different schemes.
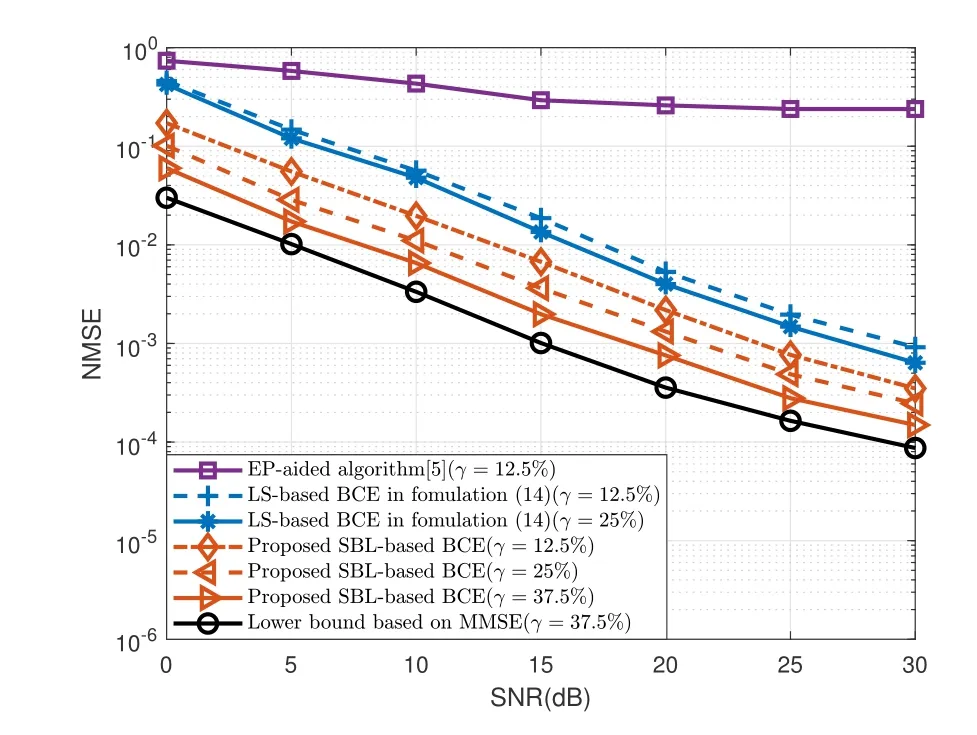
Figure 8. The NMSE performance with velocities of 685 km/h,i.e.fd=15%.

Figure 9. The BER performance with velocities of 137 km/h,i.e.fd=3%.
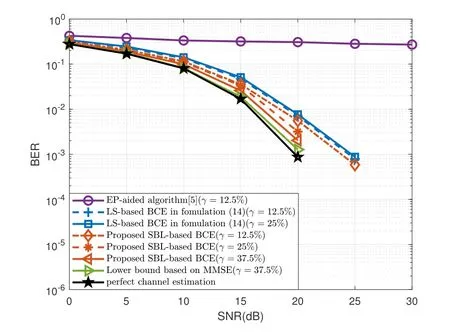
Figure 10. The BER performance with velocities of 685 km/h,i.e.fd=15%.
4.2 Simulation Result
In this section,we will illustrate the performance in terms of the bit error rate (BER) and normalized mean squared error (NMSE) of the OTFS system using the proposed channel estimation schemes,in comparison to existing EP-aided channel estimation approaches [9].The system parameters are adopted as follows: Carrier frequency of 4GHz,sub-carrier spacing of 15KHz,M=32,N=16 and 16-QAM modulation.The Extended Vehicular A (EVA) model[25] specified by 3GPP for high-mobility scenarios is adopted.Without loss of generality,we simulate some scenarios with normalized Doppler frequencyof 3% and 15%,corresponding to the velocities of 137 km/h and 685 km/h,whereis maximum Doppler frequency.In the simulation,γis defined as the pilot overhead,and assumes that the unknown path of the channel is the CP length of the channel,i.e.NCP=12.
In the system,we compare the LS-based BCE with pilot overhead of 12.5% and 25%,and the SBLbased BCE with pilot overhead of 12.5%,25% and 37.5% respectively.Additionally,the state-of-the-art scheme,i.e.the EP-aided channel estimation method(γ=12.5%),is included for comparison.In this process,the performance of the BCE algorithm based on MMSE criterion is regarded as the lower bound,whereγ=37.5%.
Figure 7 and 8 demonstrate the NMSE versus SNR in velocities of 137 km/h and 685 km/h.By observing the proposed SBL-based BCE,it can be seen that when the pilot overhead is the same,i.e.12.5%,the NMSE gain of the SBL-based BCE is much better than EP-aided,which illustrates that the OCR is better to reflect the variation of the real channel than the traditional channel model.When the pilot overhead(γ=12.5%) of the SBL is less than the LS-based BCE(γ=25%),its performance gain is about 5dB.It shows that the proposed SBL-based BCE is superior to the LS-based BCE in different Doppler environments under the same OCR channel model.
The BER performance of Figure 9 and 10 is observed,where the black line represents the perfect channel estimation.It can be seen that for the proposed SBL-based BCE of BER=10-4,the required SNR with velocities of 137 km/h and 685 km/h are 15dB and 25dB respectively,which also proves that the proposed algorithm can well cope with high Doppler environment and is robust to different speeds.
Additionally,it’s found that the BER and NMSE performance of the OCR restored by the BCE algorithm is better than the discrete DD domain channel response restored by EP-Aided channel estimation algorithm in different Doppler environments.And whenfdis 15%,the EP-Aided channel estimation algorithm has obvious performance bottleneck,while the performance curve of the algorithm based on OCR channel model continues to decline.The reason is that,OCR reflects the changes of sampling points within a symbol,whereas EP-Aided algorithm ignores these changes.In this case,as the Doppler frequency increases,the changes of sampling points will be more severe,since the error of EP-Aided algorithm will be larger.By the means,it is proved the accuracy and superiority of the OCR channel model derived from time domain.
V.CONCLUSION
In this paper,we derive a DD domain channel model from the time domain perspective,which captures the variation of each sampling point in a symbol.At the same time,we adopt the BEM and the relationship between the time domain model and the DD domain model to reduce the dimension of the channel model,so as to turn the original underdetermined problem into an overdetermined problem.Finally,in terms of the unknown channel path,the SBL algorithm is used to estimate the basis coefficients based on the sparsity of channel delay domain without any priori information of channel.Complexity analysis and simulation results show the superiority of the proposed channel estimation algorithm in complexity,BER and NMSE performance.
ACKNOWLEDGEMENT
This work was supported by the Natural Science Foundation of Chongqing(No.cstc2019jcyj-msxmX0017).
杂志排行
China Communications的其它文章
- Coordinated Planning Transmission Tasks in Heterogeneous Space Networks: A Semi-Distributed Approach
- Secrecy Rate Maximization for 6G Cognitive Satellite-UAV Networks
- Secure Transmission in Cognitive Radio Networks Using Full-Duplex Technique with Outdated CSI
- Computation Rate Maximization in Multi-User Cooperation-Assisted Wireless-Powered Mobile Edge Computing with OFDMA
- A Novel Multi-Granularity Flexible-Grid Switching Optical-Node Architecture
- Model-Free Adaptive Frequency Calibration for Voltage-Controlled Oscillators
