Channel Estimation for OTFS System over Doubly Spread Sparse Acoustic Channels

Yang Zhang,Qunfei Zhang,Chengbing He,Chao Long

School of Marine Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China

Abstract: This paper addresses sparse channels estimation problem for the generalized linear models (GLM) in the orthogonal time frequency space(OTFS) underwater acoustic (UWA) system.OTFS works in the delay-Doppler domain,where timevarying channels are characterized as delay-Doppler impulse responses.In fact,a typical doubly spread UWA channel is associated with several resolvable paths,which exhibits a structured sparsity in the delay-Doppler domain.To leverage the structured sparsity of the doubly spread UWA channel,we develop a structured sparsity-based generalized approximated message passing (GAMP) algorithm for reliable channel estimation in quantized OTFS systems.The proposed algorithm has a lower computational complexity compared to the conventional Bayesian algorithm.In addition,the expectation maximum algorithm is employed to learn the sparsity ratio and the noise variance.Simulation and experimental results show that the proposed algorithm has superior performance and low computational complexity for quantized OTFS systems.

Keywords: OTFS;doubly spread UWA channel;delay-Doppler domain;GAMP

I.INTRODUCTION

Underwater acoustic channels are considered as one of the most challenging communication media [1].In contrast to terrestrial radio channels,underwater acoustic (UWA) channels have severe transmission loss,limited distance and dependent bandwidth,time varying multipath propagation,and severe Doppler spread.Generally,acoustic channels exhibit both dispersion in time (delay spread) and frequency (Doppler spread).The channels of this type are referred to as doubly spread channels [2].Conventional OFDM is that it does not perform well in doubly spread channels [3],especially it cannot handle large Doppler spread in rapidly time-varying UWA scenarios.Recently,orthogonal time frequency space(OTFS) modulation has emerged as a potential technology,aims at offering as reliable communication as possible over doubly spread channels [4-6].In this paper,we focus on doubly spread channel estimation with low-resolution quantization for OTFS UWA system.

For OTFS channel estimation,the authors in[7]propose a threshold-based channel estimation method via designing a single pilot pattern in the delay-Doppler domain.However,this channel estimation performance is sensitive to pilot power and results in high peak-to-average power ratio.In order to further improve the performance of channel estimation,multiple pilot schemes have been proposed one after another.In [8],author proposed a three-dimensional structured orthogonal matching pursuit algorithm to estimate the delay-Doppler-angle domain channel via exploiting the three-dimensional structured sparsity.But this scheme does not consider the fractional Doppler case.To address this weakness,the authors in [9]proposed a deterministic pilot design with a fractional Doppler in practical system.Although the proposed scheme achieves better channel estimation performance,it is an OFDM-based OTFS system with multiple CPs,resulting in high spectral efficiency.Further,several channel estimation schemes based on the sparse Bayesian learning framework are proposed in turn.The authors in [10] proposed an off-grid channel estimation with sparse Bayesian learning for OTFS Systems,the proposed scheme enjoys lower complexity and superior performance.However,the authors only considered channel estimation with ideal waveforms,which are not feasible in practice.Meanwhile,several channel estimation schemes based on sparse Bayesian learning(SBL)is also proposed in[11]and[12],which effectively improves the performance of channel estimation,but the proposed scheme still has high complexity.In [13] an efficient message passing algorithm is developed to recover the structured sparse signal,which is mainly based on factor graph presentation.However,the proposed algorithm above only consider the ideal processed signals with infiniteresolution quantization.As a result,these algorithms only exhibits significant performance with standard linear models(SLM)in OTFS systems.

Nevertheless,with the rapid development of the communication technology,the future communication transmission rate will be greatly improved,which means that the sampling rate of the analog-to-digital converter must be increased.Under the heavy quantization,the SLM is not applicable and the nonlinear effects have to be taken into account.To make the OTFS practical,we consider the quantization of the received signal under a generalized linear models(GLM) model for channel estimation.Quantizationbased channel estimation techniques have been extensively studied in multi-input multi-output(MIMO),direction of arrival (DOA),etc.,and it has superior advantages in terms of low cost and complexity[14-16].

Taking this into consideration,we propose a structured sparsity-based generalized approximated message passing(GAMP)algorithm for channels estimation,where the quantization of the processed signals is considered.Message passing algorithms for compressed sensing have attracted much research interest due to their fast convergence and low computational complexity [17].Especially channel estimation techniques based on message passing algorithms have superior performance in terms of complexity and convergence ratio.In recent years,several channel estimation schemes based on message passing algorithms have also been proposed in UWA communication[18,19],and these methods exhibit robust performance in UWA communication systems.Our main contributions can be summarized as follows:

•We first give a discrete-time formulation of OTFS system in the delay-Doppler domain.Moreover,the input-output relationship shows that the timevarying channel exhibits the features of structured sparsity in the delay-Doppler domain for OTFS systems.Further,we formulate the sparse channel estimation problem in the OTFS system as a sparse recovery problem.The multi-pilot symbols and guard intervals are arranged in the delay Doppler lattice,where the guard interval is to avoid interference between the pilots and data symbols.

•We propose a structured sparsity-based GAMP algorithm to recover sparse channel from quantized signals,and aim to improve sparse channel estimation performance with fast and stable convergence.In contrast to conventional approximated message passing (AMP) algorithms with SLM,the proposed algorithm not only keeps the robustness of the AMP algorithm but also achieves a great reduction of computational complexity.Notably,to enhance the estimated performance in practical scenarios,an expectation maximization(EM) algorithm is employed to jointly learn the channel prior parameters and noise variance.Finally,a weighted damping factor strategy is introduced to further improve the performance.

•The proposed scheme was evaluated through several simulations and real scenario experiments in OTFS systems.Both simulations and analysis show that the proposed structured GAMP algorithm exhibit advantages in terms of computational complexity and performance under a realistic channel model.To sum up,both simulation and experiment results demonstrate that the proposed algorithms are more effective for quantized OTFS systems.

The remainder of the paper is organized as follows.In Section II,we briefly describe the OTFS system model,and give a discrete-time formulation of OTFS underwater acoustic system.Then we formulate the channel estimation as a structured sparse signal recovery problem,and propose a message passing algorithm based channel estimation technique in Section III.Simulation results and experimental results are given in Sections IV and Sections V,respectively.Finally,conclusions are drawn in Section VI.

Notation: We employ lowercase and uppercase boldface letters denote vectors and matrices,respectively.Normal letters denote scalars.(·)*,(·)T,(·)H,and (·)-1denote the conjugate,transpose,conjugate transpose,inversion,respectively.INdenotes the identity matrix of sizeN × N.A matrix of sizeN ×Mwith complex entries are denoted by CN×M.⊙denotes Hadamard product.vec(·)and invec(·)denote the vectorizing of a matrix and invectorizing of a vector,respectively.[·]Ndenotes the modulus operation.Moreover,the complex Gaussian distribution with meanµand varianceσ2is denoted byCN(µ,σ2).

II.SYSTEM MODEL

In this section,we first present a brief description of OTFS modulation over time-varying UWA channels.Next,the input-output relations of the OTFS system is given for doubly spread acoustic channels,and in the end we reformulate the OTFS relation based on the sparse channel in vector form.The block diagram of OTFS system is illustrated in Figure 1.

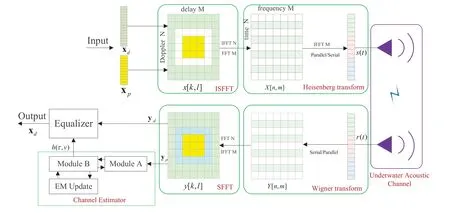
Figure 1. Block diagram of OTFS system.

2.1 Transmitted Signal

At the transmitter,the complex vector symbols x∈CNM×1are firstly arranged on a two-dimensional delay-Doppler lattice.Then the mapped twodimensional symbolsx[k,l] in the delay-Doppler domain to time-frequency domain symbolsX[n,m]using the inverse symplectic finite Fourier transform(ISFFT),wherek=0,···,N-1,l=0,···,M-1.NandMdenote the number of time slots and the number of subcarriers,respectively.This mathematical operation is given by[4]

wheren=1,···,N -1 is the time index,m=1,···,M -1 is the subcarrier index.Next,a timefrequency modulator converts the samplesX[n,m]to a continuous time waveforms(t) with a transmit waveformgtx(t)by Heisenberg transform as

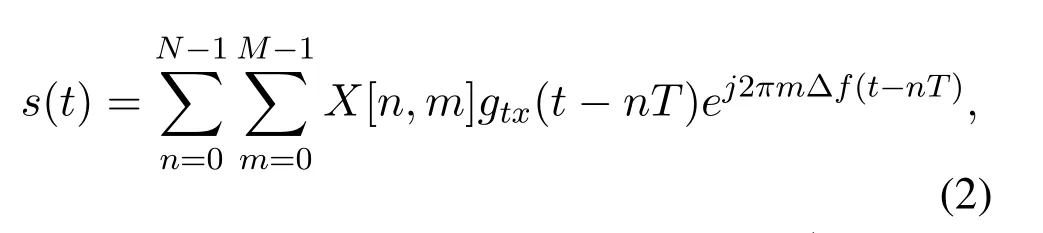
where Δfis subcarrier spacing andT=1/Δfis the symbol duration.Note that the practical rectangular pulsegtx(t)is used in this paper.

2.2 Underwater Acoustic Transmission and Reception

In general,the signals(t)is transmitted over a conventional linear time-varying channel,which is described by a time-delay spread functionu(τ,t).Here,u(τ,t)is a complex baseband impulse response that characterizes the channel response with delayτand geotimet.The received signalr(t)is represented as

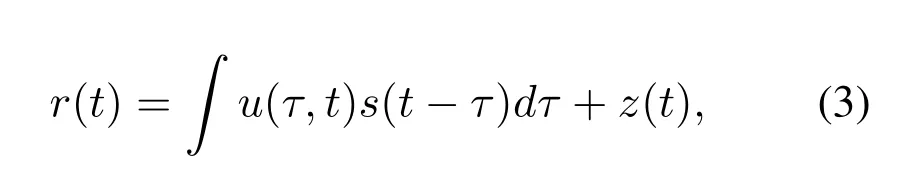
wherez(t)denotes additive noise in the time domain.In time-delay spread channel,the existing modulation techniques have the following limitations[20]:

1) the conventional single dominant Doppler shift compensation scheme is difficult to deal with large Doppler spreads,which will incur performance degradation in the Severe Doppler spread channel.

2) Channel estimation needs to be updated frequently to track the latest channel state information over the rapidly time-varying channel,which considerably increases the computational burden at the receiver.

In contrast to the existing modulation schemes that experiences over time-varying channels based on time-delay spread functions,OTFS modulation works on the time-varying channel with a complex impulse responseh(τ,v),which is described by a delay-Doppler spread function.The delay-Doppler spread function of the time-varying channel is defined as the Fourier transform ofu(τ,t)with respect to timet[21],which is given by

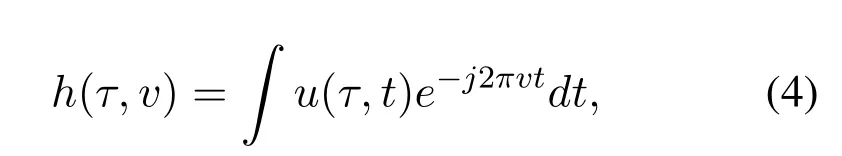
wherevdenotes the Doppler spread.Further,we bring the inverse Fourier transform ofh(τ,v) into (3),and equation(3)is rewritten as

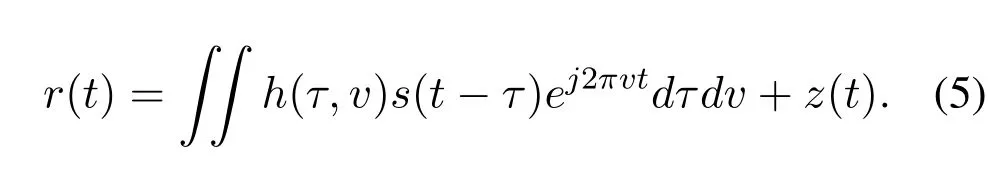
A reasonable physical interpretation for the above message transmission process is:channel model in(5)can also be considered as multipath arrivals become resolvable,which characterizes the physical propagation of acoustic rays in the wireless scenario[2].The multipath effect of wireless channels could be demonstrated as the effect of the direct path,the surfacereflected path,the bound-reflected path,the multireflected paths,and so on [22,23].Thus,the timevarying channel characterized by the delay-Doppler impulse response in real underwater scenarios tend to be distinct sparsity.The delay-Doppler channel modelh(τ,v) can be further characterized as a channel model withpaths is written as

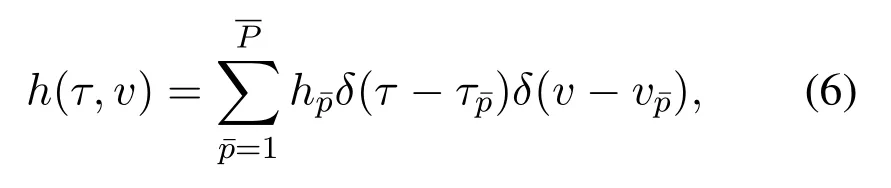
whereis the number of propagation paths;represent the path gain,delay,and Doppler shift associated with-th path,respectively,andδ(·)denotes the Dirac delta function.Equation(5)can be further discretized,we usen′to denote the discrete index of timet.Thus,the discrete-time input-output formulation is as

2.3 Received Signal

At the receiver,the time-frequency signalY[n,m] is obtained by performing matched filtering on the received signalr[n′].The discrete output of the matched filter is given below

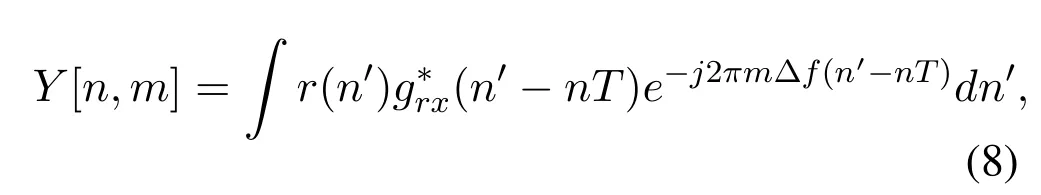
wheregrx(n′) is the discrete form of continuous receive rectangular waveformgrx(t).Then,here we give the OTFS input-output relation with the rectangular pulse in the time-frequency domain [24],the specific equation is given as

whereHn,m[n′′,m′′]is a composite channel response in the time-frequency domain,which includes the transmit pulse,the double-spread channel impulse response,and the receive pulse.Hn,m[n′′,m′′]is given by

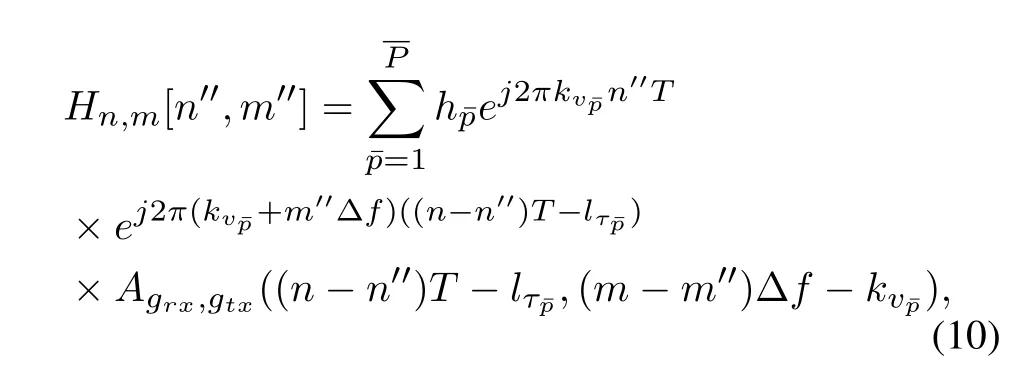
whereAgrx,gtx(nT,mΔf) indicates that the crossambiguity function in discrete form betweengtx(n′)andgrx(n′)is given by

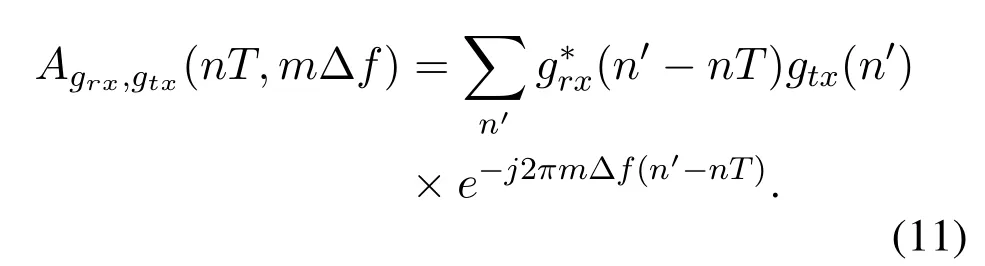
By observation we can see in (9) that the second term from the samplesX[n,m′] at different frequenciesm′ mis the total interference as inter carrier interference,and the third term is the accumulated inter symbol interference from the sampled signalX[n-1,m′]in the previous time slotn-1.

Next,the symplectic finite Fourier transform(SFFT) is performed on the output signalY[n,m] in the time-frequency domain to obtain the final received symboly[k,l]in the delay-Doppler domain

2.4 Delay-Doppler Domain Analysis

In this subsections,we presents an explicit inputoutput relation and reformulate the OTFS system relation in the delay-Doppler domain.The detailed derivation is found in [24],here we directly give the inputoutput relation with the rectangular waveform as

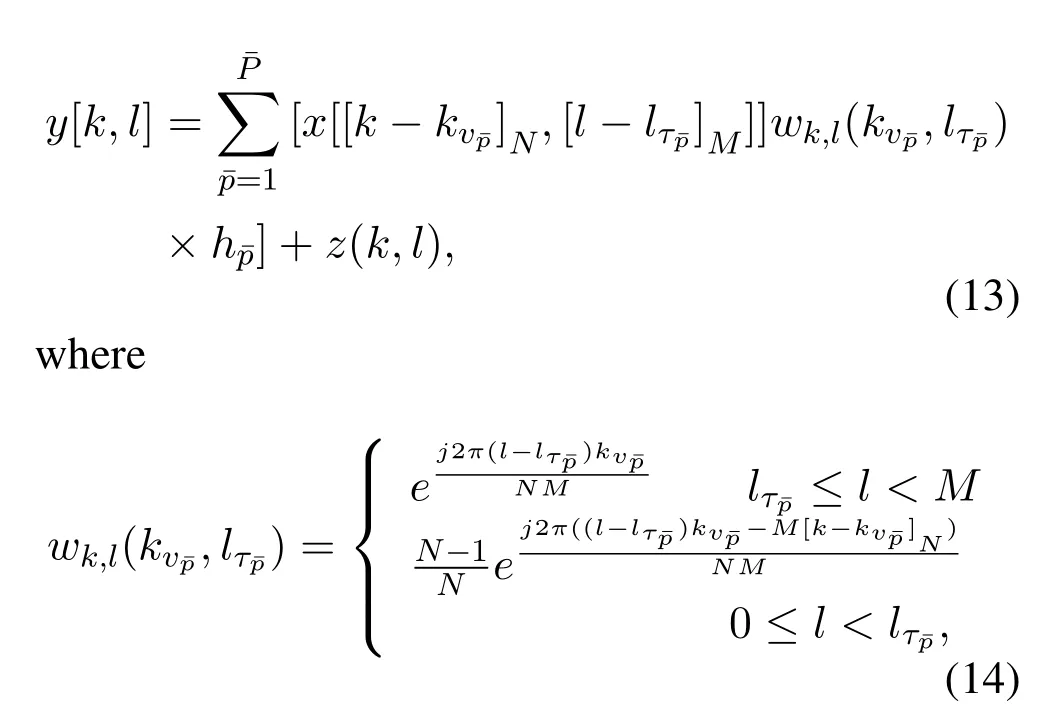
wherez[k,l] denotes the noise symbol in the delay-Doppler domain.Through the analysis in(13),we can see that the received signaly[k,l] is formed by three parts,which are the circularly shifted transmit signal,the phase interference,and the channel gain.

Next we give the received signal in matrix form.First we defnie a row vector xn′ ∈and row vector wn′ ∈,whose elements from cyclically shifted transmit symbols and phase interference in the-th path,respectively.xn′and wn′can be given by

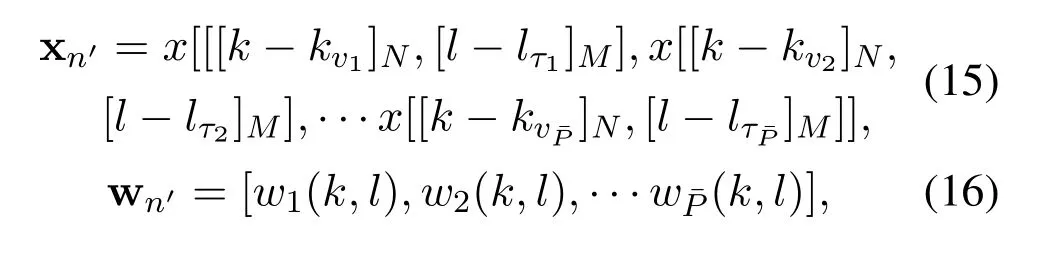
wheren′=Nl+k+1 denotes the(k,l)-th element on the delay-Doppler grid.In addition,we define a vectorwhose elements from the gain of the-th path,i.e..Then,the received signal in(13)can be written as

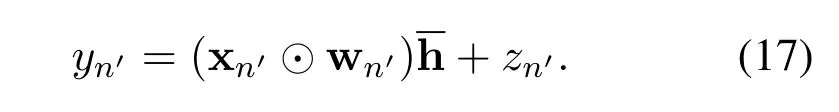
The stackingyn′’s into anNMdimensional vector y yields the following system of equations

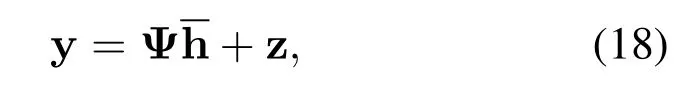
where the composite matrix Ψis comprised of xn′⊙wn′as its rows:Ψ=[x0⊙w0;···;xNM-1⊙wNM-1].The received signal in Equation(18)can be further quantified and written as

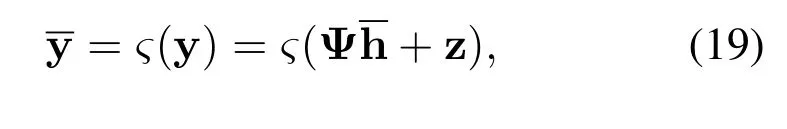
whereς(·) is the complex-valued quantizer,which is found in[25].

Through the above analysis,we can clearly observe that the received signal y is the product of the channel vector h and the composite matrix Ψ in(18).Ψ is the stack of the inner product of then′-th transmit symbol xn′and then′th phase interference wn′for corresponding cyclic shifts in different dimensions.We reformulate the system model for the OTFS in (17)and(18)to give the relation between the channel vector and the composite matrix in the delay-Doppler domain,which contributes to the subsequent channel estimation problem.

III.THE PROPOSED SCHEME IN OTFS SYSTEMS

We first develop a delay-Doppler channel estimation scheme by designing the corresponding pilot pattern for the OTFS system,and then we formulate a sparse signal recovery problem.Next,the GAMP algorithm is proposed to estimate double-spread channels,and its performance and complexity are analyzed.

3.1 Virtual Representation and Problem Formulation

For the doubly Spread channel estimation problem in OTFS systems,it can be described by some potential physical parameters.However,in the case of the discrete path model(6),the channel estimation model in (18) is realistically difficult to analyze and learn due to its nonlinear[10].Thus,the virtual channel model is introduced,which aids a low-dimensional approximation of the discrete path model by uniformly sampling[26].Specifically in OTFS systems,the discrete path model in (6) can be represented as a twodimensional discrete channel model by uniform sampling in the delay dimension and the Doppler dimension.The delay resolution and Doppler resolution of the samples are fxied,i.e.That is,the two-dimensional virtual channel in the delay-Doppler domain can be given as

whereh[lτi,kvj]are termed as the virtual channel coefficients in the delay-Doppler domain.The delay shiftτiand the Doppler shiftvjare given by

wherelmaxandkmaxdenote the maximum number of resolvable delays and Doppler shifts within the delay-Doppler spreading function,respectively.lτiandkvjdenote the virtual index of delay dimension and the virtual index of Doppler dimension,respectively,which correspond to the continuous delayτiand Dopplervj.

Next,we introduce a multiple-pilot estimation scheme in the delay-Doppler domain,as shown in Figure 2.On the delay-Doppler grid,the pilot symbols are arranged in the middle to prohibit additional frame interference,and the guard intervals are arranged around the pilot region to avoid contamination of the pilot symbols.Note that the interval between pilot symbols and data symbols will be wider than the maximum Doppler shift and the maximum delay shift in different dimensions,respectively.We then employ the truncated received pilots to estimate the channel.In addition,our pilot energy is consistent with the data energy with a low signal-to-noise ratio (SNR),which avoids a high peak-to-average power ratio.The transmitted symbols are written as

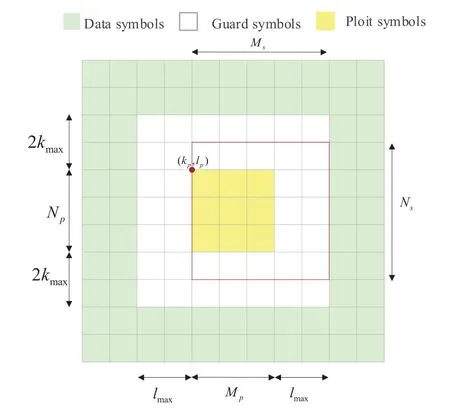
Figure 2. The pattern of transmitted symbols includes data,pilot,and guard intervals.

wherekpandlpdenote a baseline position of the pilots,Npdenotes the number of pilots in the Doppler dimension,Mpdenotes the number of pilots in the delay dimension.xddenotes the transmitted data symbol,which is arranged on a grid outside the range of the pilot symbols and guard intervals.

At the receiver,we extract the symbols of the truncated region as the received pilot vector ypin(13)for channel estimation.The truncated region is marked with a red box in Figure 2.To satisfy the minimum pilot overhead,the size of the truncation region is given by

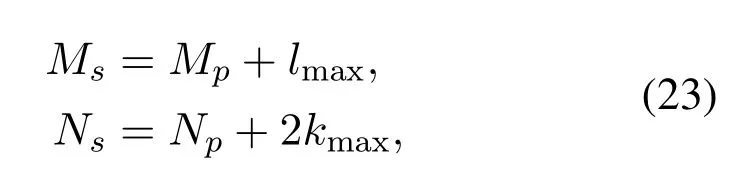
whereMsandNsdenote the size of the truncation region in the delay dimension and the Doppler dimension,respectively.So the total number of truncated regions isLp=NsMs.Furthermore,the input-output relationship based on pilot symbols is rewritten in(13)as

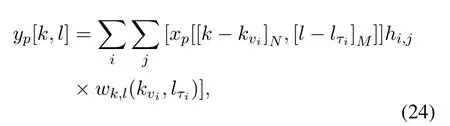
Similarly,the discrete pilot model in (24) can be rewritten in matrix form as

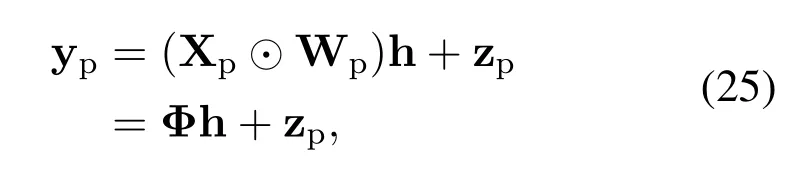
where h=vec(H),H∈C(2kmax+1)×(lmax+1)denotes the two-dimensional virtual channel matrix in the delay-Doppler domain,Hj,i=h[kvj,lτi].So the total number of two-dimensional virtual channels isLh=(2kmax+1)×(lmax+1).Φ=Xp⊙Wp∈CNM×Lha composite matrix;Wp∈CNM×Lhis the phase compensation matrix.Xp∈CNM×Lhis corresponding pilot matrix.zp∈CNM×1is the additive noise in corresponding pilot position.Here we assume that zpfollows a white Gaussian distribution with zero mean and varianceσ2.Finally,the pilot signal can be quantized by a quantizer as

In the channel estimation,,which means that the spreading function has few nonzero elements compared with its dimensionLh.Thus,h is a structured sparse vector in (25),and the channel estimation problem in(25)can be formulated as a structured sparse signal recovery problem.we shall treat h as a deterministic but unknown vector.Next,we propose a GAMP algorithm to recover the sparse vector h and further obtain the estimates ofhi,j,lτiandkvifor the double spread channel.In particular,the noise variance and channel prior distribution can be estimated via the EM algorithm.

3.2 GAMP Algorithm for Channel Estimation

In this subsection,we will give a detailed description of the proposed structured sparsity-based GAMP algorithm to achieve unknown sparse vector recovery.Moreover,our proposed algorithm can reap better performance and lower complexity than existing work[12,11],owing to the approximate message with low complexity heuristics.The block diagram of the proposed scheme is illustrated in the receiver part of Figure.1,which contains two modules,i.e.module A and module B.Module A employs a conventional minimum mean square error estimate in(25)to obtain the quantized received signaland noise varianceσ2,and the corresponding posterior mean and variance are denoted.Then extrinsic messagesandof module A is fed back to module B as an input message[25].Module B is a structured estimator to further refine the performance of the estimator.The sparse GAMP algorithm is employed as a structured estimator,whose input messages from module A and the prior distribution of the channel.Finally,the extrinsic messagesof module B are passed to module A as a priori information in(25).Both modules are executed iteratively until convergence.

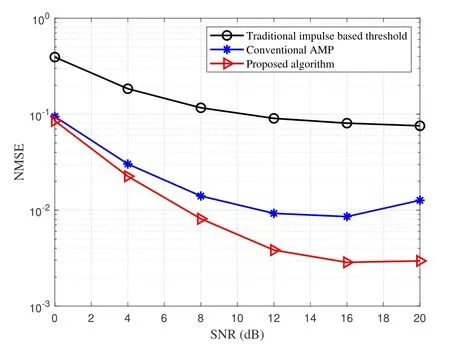
Figure 3. The NMSE performance comparison versus the SNR.

3.2.1 Brief Description of Module A

In this module,the posterior probability of the channel vector ypis given by

Next,the mean and variance of the extrinsic message are calculated by

3.2.2 Proposed Structured Sparsity-based GAMP Algorithm

In general,the optimal problem in (25) is estimated using the minimum mean square error,which is equivalent to estimating the posterior mean of the channel vector h given as

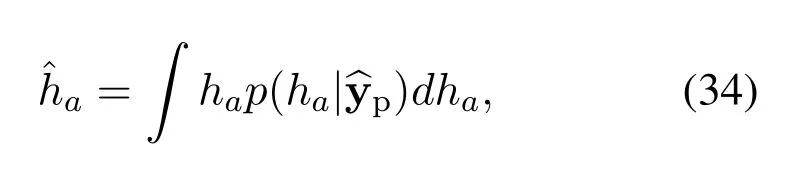
wherehadenotes thea-th element of the channel vector h,a=(2K+1)(lτi) +kvj+κvj.The conventional solution in (34) is optimal Bayesian channel estimation[27],which is dedicated to optimal performance.However,optimal Bayesian estimation has prohibitive complexity for marginal probability calculations.Therefore,in order to calculate the marginal posterior probability with low complexity,we resort to the GAMP algorithm [17,28].GAMP is an iterative message passing algorithm that employs an approximate message mechanism to achieve low computational complexity.

Next,we will give a detailed description of the proposed structured sparsity-based GAMP estimator.To start with,the AMP algorithm decouples the matrix problem intoNMscalar estimation problem.Based on this premise,the modelis given as an additional white Gaussian noise as

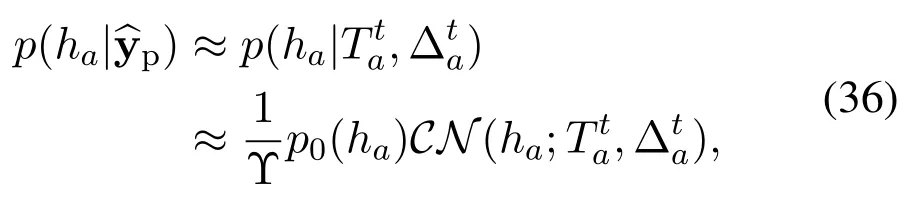
where Υcis a normalization factor andp0(ha)denotes the a priori distribution ofha.The asymptotic estimateofhaand variancein thet-th iteration can be calculated as

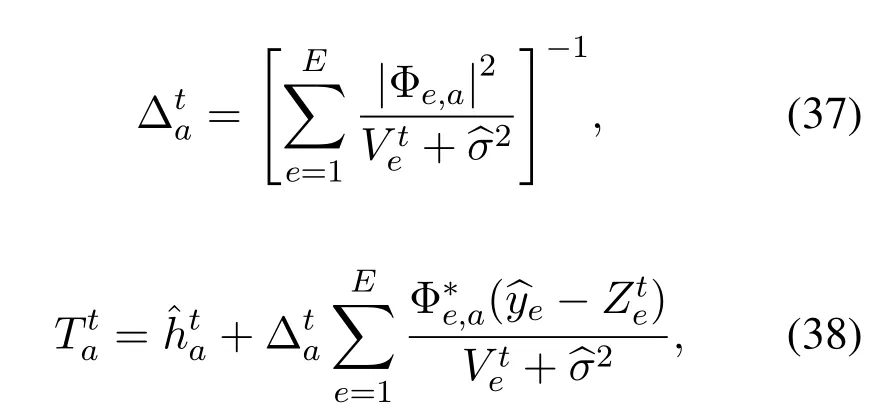
where messagesare updated at the factor nodes as follows

wheret=0,...,tmaxdenotes the iteration count;is the posterior variance ofha,eandadenote the index of the row number E and the index of the column number A in Φ,respectively.denotes thee-th element of the pilot vector.

To characterize the sparsity of the channel vector h,we employ a Bernoulli-Gaussian distribution to model the prior distribution of h[29],which can be given by

where 0＜λ ＜1 denotes the sparsity ratio,i.e.,the probability ofhlbeing non-zero,δ(·)is the Dirac delta function.µpri=0 denotes the priori mean of the channel gain,andvpriis the a priori variance of the non-zero part.

Further,the posterior probability distribution ofhacan be calculated based on the prior model in(36).The detailed derivation is given in [30],here we directly present the results as

whereis referred to as the belief indicator.As a result,the posterior mean and variance of the channel gainhacan be calculated by

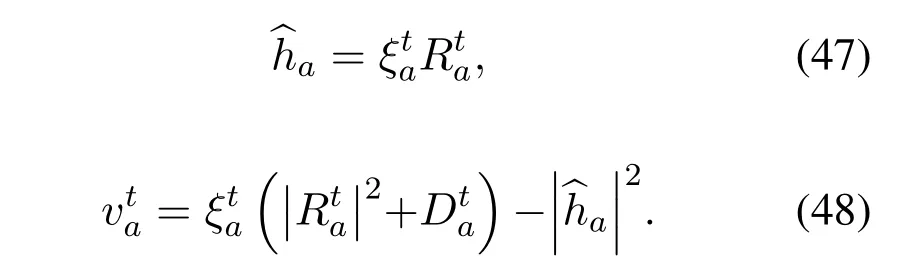
In the above key steps,we assume that the receiver is fully knowledge of the a priori distribution of the channels{µpri,vpri,λa}and the noise varianceσ2for the GAMP algorithm.But in real underwater acoustic communication it is difficult to obtain these parameters.Hence,we employ the EM algorithm to learn the unknown hyperparameters in the practical system.

The EM algorithm is an iterative technique that increases a lower bound on the likelihoodat each iteration [31],whereis unknown hyperparameter.Briefly,we give a previous parameter estimateθt,the EM update for the parameters is achieved by

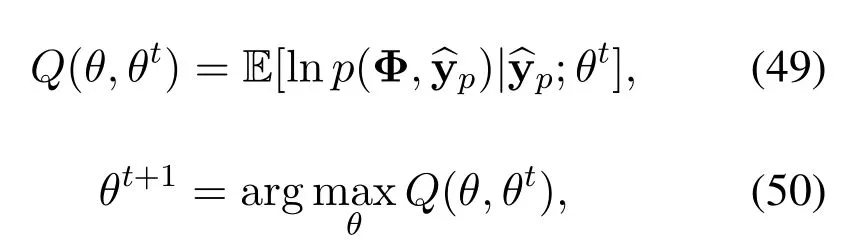
where E[·|y;θt] denotes the expectation conditioned on measurements y with parametersθt,i.e.,the expectation is with respect to the posterior distributionp(h|y;θt).By setting the derivative of (49) with respect to one element ofθto zero,the update rules of the hyper-parameters are obtained as[30]

Note that we initialize the prior parameters with reference to [32],and GAMP algorithm and parameter learning are performed iteratively until convergence.In addition,an appropriate damping factor is employed to improve the convergence speed.Finally,the posterior mean and variance of the channel vector h are calculated as a priori message in module A by[25]

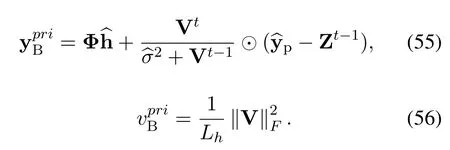
To sum up,we can observe that message passing is iteratively executed between module A and module B,which is referred to as structured Turbo-GAMP algorithm.The proposed algorithm is summarized inAlgorithm 1.In particular,the channel estimation problem is decoupled into a scalar estimation problem in(35),resulting in the proposed algorithm having lower complexity than state-of-the-art channel estimation algorithms in OTFS systems.

3.3 Computational Complexity Analysis

The computational complexity analysis is important in the hardware implementation for practical communication,so we briefly analyze the computational complexity of the proposed algorithm.Here we only consider the maximum number of complex multiplications as an operational analysis.The complexity of the proposed structural sparsity-based GAMP algorithm is order ofO((7LpLh+16Lp+20Lh)tmax);The computational complexity of the Turbo structure is order ofO((LpLh+Lp)gmax),so the total computa-tional complexity is order ofO(LpLh(7tmax+gmax)+Lp(16tmax+gmax)+20Lhtmax).Specifically,the complexity of the Turbo-GAMP algorithm scales linearly with the number of pilot symbolsLpand channel sizeLh.In addition,the computational complexity of the proposed algorithm is compared with the conventional SBL algorithm[11],variational Bayesian algorithm[33,34],and traditional impulse based channel estimation methods(threshold-based method)[7].The computational complexity of different algorithms is given in Table 1.We can observe that the proposed algorithm has approximately linear computational complexity,while the computational complexity of the conventional method is more than the cubic computational complexity.Moreover,the thresholdbased method shows worse performance despite its low complexity.The fact that the proposed algorithm decouples the matrix into scalars using approximate messages,thus the matrix inversion is avoided.As a result,the proposed algorithm is more attractive than state-of-the-art algorithms for solving the channel estimation problem in OTFS systems.

Table 1. Computational complexity of different algorithms.

IV.NUMERICAL SIMULATIONS

In this section,we perform several simulations to verify the effectiveness of the proposed algorithm in terms of channel estimation accuracy and BER performance in UWA scenarios for OTFS modulation.The transmitted symbol adopts quadrature phase shift keying(QPSK)modulation,which is mapped onto a twodimensional delay-Doppler grid with sizeN=16 andM=64.And with reference to [35],we set the related parameters to characterize the real underwater scenario.Here we set the carrier frequency isfc=6 kHz,the bandwidth is B=4 kHz,and the speed of sound isc=1500 m/s.Furthermore,the symbol sampling interval and the slot duration are given byTs=0.25 ms andT=16 ms,respectively.Note that the pilot symbols are also obtained via QPSK,which maintains the same energy as the data symbols to avoid high peak-to-average power ratio.

We consider a sparse underwater acoustic channel from [36].The paths amplitudes follows a Rayleigh distribution with the average energy growing exponentially decreasing profile with delay,where the difference between the first path and the last path is 20 dB.Further,we consider that the maximum delay spread is set tolmax=7,maximum Doppler shift iskmax=3.Each tap have a single Doppler shift that is randomly generated through Jake’s formulaki=kmaxcos(θi),whereθidenotes uniformly distributed between-πandπ[24].In addition,we set the initialization of the convergence indicator to beη=10-5.To evaluate the performance of the proposed algorithm,the normalized mean square error is employed as a conventional evaluation criterion,which is defined by

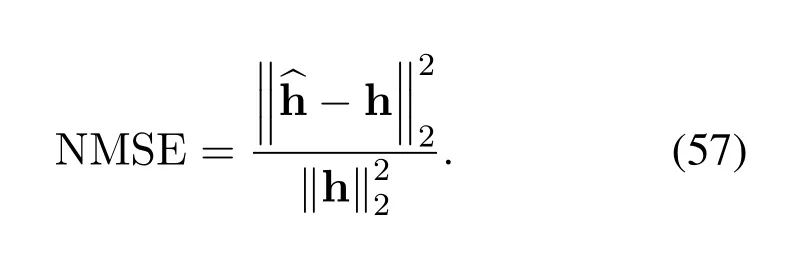
The traditional impulse pilot scheme based on channel estimation techniques is presented as a benchmark[7].We also present the conventional AMP algorithm with SLM to process the quantized signal as a comparison in the OTFS system.We will compare the NMSE performance of the proposed structure sparsity-based GAMP algorithm based on channel estimation technique,traditional impulse pilot,and the conventional AMP algorithm based on the channel estimation technique against the SNR,the pilot overhead ratio.

4.1 Performance Analysis

In Figure 3,we present the NMSE performance comparison versus SNR.We observe that the NMSE performance of the proposed structured sparsity-based GAMP algorithm based on channel estimation is substantially improved with increasing SNR.Moreover,the proposed algorithm based on channel estimation technique significantly outperforms the traditional impulse based channel estimation technique.The NMSE performance of traditional impulse based channel estimation technique is inferior due to inaccurate threshold decisions,and this scheme causes unreliable estimators from unpredictable noise interference.The proposed algorithm is also distinctly better than the conventional AMP algorithm based on channel estimation technique with different SNR,because the proposed scheme takes full advantage of the nonlinear module to process the quantized signals in the OTFS system.Moreover,we adopt the EM algorithm to learn the channel parameters and noise variance adaptively,resulting in a more accurate channel estimator.Hence,our proposed scheme can achieve accurate delay-Doppler channel estimation in OTFS system.

In Figure 4,we give the BER performance comparison against the SNR,where the BER of the perfect the channel state information is used as a benchmark.We resort to the conventional minimum mean square error (MMSE)algorithm as a symbol detector in OTFS systems.We observe that the proposed structured sparsity-based GAMP algorithm achieves satisfactory BER performance,which is closest to the case of perfect channel state information in the OTFS system.Moreover,the BER performance of the proposed algorithm is better than that of the conventional AMP algorithm under different SNR,because the proposed algorithm obtains more accurate channel state information.The traditional impulse-based channel estimation method obtains inaccurate CSI,which leads to worse BER performance.

Figure 4. The BER performance comparison versus the SNR.

The computational complexity analysis is the crucial issue in this paper.Specifically,the total number of pilot symbolsLpand channel sizeLhdetermine the order of complexity in the conventional OTFS channel estimation.Figure 5 shows the computational complexity of the proposed GAMP algorithm,the conventional SBL algorithm[11],variational Bayesian algorithm [33,34],and the threshold-based method as a function of channel size and number of pilot symbols.From Figure 5,it can be observed that the thresholdbased method has the lowest complexity,however it shows poor performance.We can also observe that the complexity of the proposed algorithm is significantly lower than other conventional channel estimation methods in terms of complex multiplication.This is because the computational complexity of the proposed estimator scales with the number of channel size or pilots number,while other algorithms are at least the cube of the number of pilot symbols or channel size for the computational complexity.In this way,it can be concluded that the proposed channel estimation scheme is effective in terms of computational complexity.

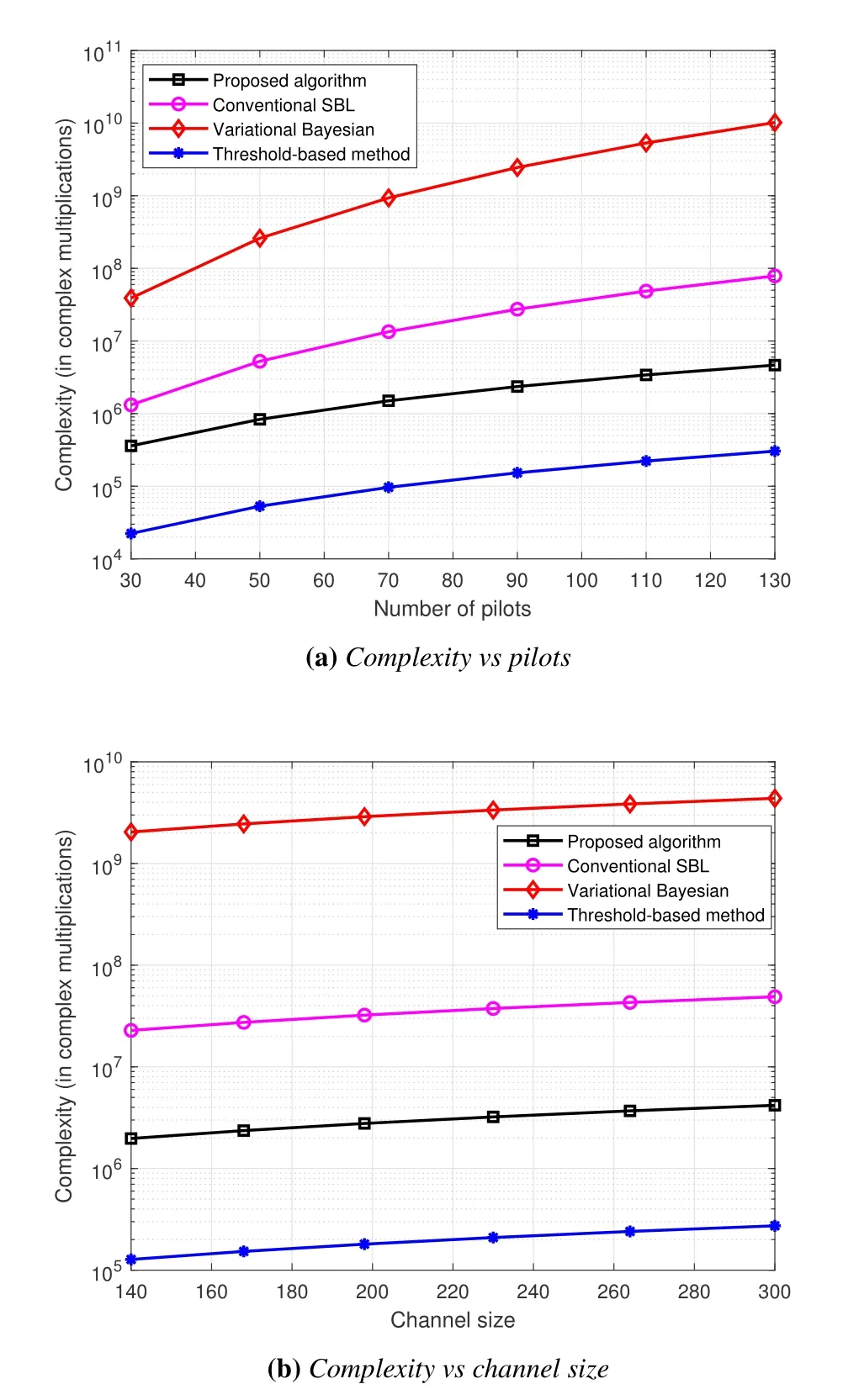
Figure 5. Complexity comparison with proposed algorithm and other conventional algorithms.

V.EXPERIMENTAL RESULTS

We adopt the Watermark database as a available benchmark for the proposed algorithm based on UWA channel estimation [37].Watermark is released with five measurement channels from various deployment scenarios,which is driven by at-sea measurements of the time-varying impulse response.KAU1 is employed in the Watermark as a experimental scenarios to verify the effectiveness of the proposed algorithm.The channel of the KAU1 is characterized by distinct time-varying Doppler shifts,and the test conditions and platform deployment are presented in [37].We observe that the KAU1 channel is remarkably timevarying in Figure 6(a),and the propagation paths are approximately distinguished.Figure 6(b) shows the delay-Doppler function of KAU1,where the propagation paths are clustered and exhibit cluster-sparse characteristics.Moreover,the channel impulse response also scales to the Doppler dimension attributed to the time-varying Doppler shift in KAU1.Thus,the experimental channel has sparse feature in the delay-Doppler domain.Note that for ease of analysis we only select some typical path gains in KAU1,which are normalized for performance analysis.

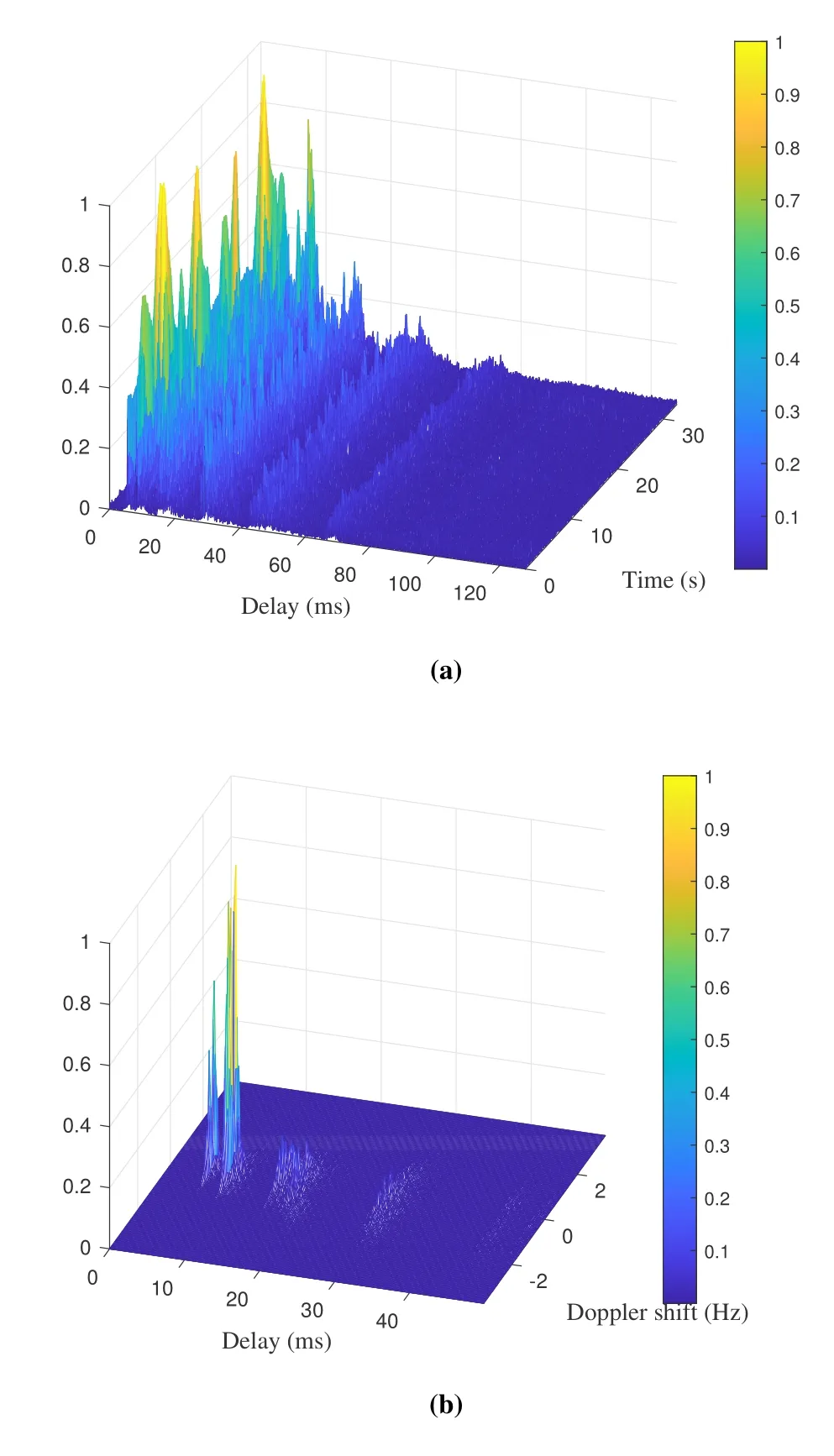
Figure 6. Time-varying channel impulse response from KAU1.

In Figure 7,we present the NMSE performance against SNR as a comparison.We can observe that the proposed algorithm based on channel estimation technique still enjoys excellent performance compared with the traditional impulse based channel estimation technique.Specifically,the proposed GAMP algorithm can improve the NMSE performance with increasing SNR over rapidly time-varying UWA channels from the KAU1 data,while the traditional impulse based channel estimation technique still remains stuck with a worse NMSE performance with same SNR.In contrast to the conventional AMP algorithm based on channel estimation technique,the proposed algorithm still shows reliable performance in time-varying underwater acoustic channels,which is due to the use of EM algorithm to learn unpredictable noise interference and channel parameters in practical underwater acoustic scenarios.Overall,we can conclude that the proposed scheme based on channel estimation technique still maintains considerable performance in real time-varying channels for OTFS systems.

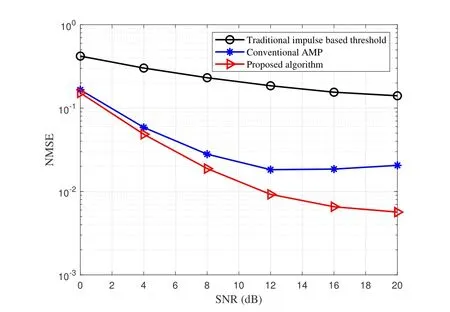
Figure 7. The NMSE performance comparison versus the SNR in KAU1 channel.

VI.CONCLUSION

In this paper,we propose a structured sparsity-based GAMP algorithm to solve the channel estimation problem for quantized OTFS UWA systems.We first reformulate the input-output relation of the OTFS system in the delay-Doppler domain.Next,the channel estimation is transformed into a sparse signal recovery problem by exploiting virtual sampling.Finally,the GAMP algorithm is employed to achieve a reliable channel quantization estimator in the OTFS system.Both simulation results and experiments verify the effectiveness of the proposed method.In particular,(1)the proposed algorithm in the simulation significantly outperforms the conventional AMP algorithm and pulse-based channel estimation techniques under different SNRs,and the structured sparsity of the channel is exploited to reduce the computational complexity;(2) the proposed method still exhibits substantial performance advantages compared with other channel estimation methods in experiment.(3) also,the proposed channel estimation technique has excellent BER performance in simulations due to more accurate channel state information obtained by the proposed algorithm.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China(No.62071383).