Max-Min Fair RIS-Aided Rate-Splitting Multiple Access for Multigroup Multicast Communications
2023-02-02TiantianLiHaixiaZhangShuaishuaiGuoDongfengYuan
Tiantian Li ,Haixia Zhang ,Shuaishuai Guo ,Dongfeng Yuan
1 School of Information Science and Engineering,Shandong Normal University,Jinan 250014,China
2 School of Control Science and Engineering,Shandong University,Jinan 250061,China
3 Shandong Key Laboratory of Wireless Communication Technologies,(Shandong University),Jinan 250061,China
Abstract: Rate-splitting multiple access (RSMA)can cope with a wide range of propagation conditions in multigroup multicast communications through rate splitting optimization.To breakthrough the grouprate limited bottleneck,reconfigurable intelligent surface(RIS)technique can be introduced to assist wireless communications through enhancing the channel quality.In RIS-aided RSMA multigroup multicasting,how to provide fair and high-quality multiuser service under power and spectrum constraints is essential.In this paper,we propose a max-min fair RIS-aided rate-splitting multiple access (MMF-RISRSMA)scheme for multigroup multicast communications,where the rate fairness is obtained by maximizing the minimum group-rate.In doing so,we jointly optimize the beamformers,the rate splitting vector at the transmitter,as well as the phase shifts at RIS.To solve it,we divide the original optimization problem into two subproblems and alternately optimize the variables.The beamforming and rate splitting optimization subproblem is solved by using the successive convex approximation technique.The phase shift optimization subproblem is solved through the penalty function method to achieve a rank-one locally optimal solution.Simulations demonstrate that the proposed MMF-RIS-RSMA scheme can obtain significant performance gain in terms of the minimum group-rate.
Keywords: multigroup multicast communications;rate-splitting multiple access(RSMA);reconfigurable intelligent surfaces(RIS);max-min fairness(MMF)
I.INTRODUCTION
Being able to simultaneously deliver the same data stream to multiple users at the same time-frequency resource,wireless multicasting technique has the remarkable ability in enhancing spectrum efficiency and has gained extensive attention in recent years[1-6].The multicast paradigm has been expanded from single-group unicast [1,2] to multigroup multicast[3,4],even to hybrid unicast and multicast [5,6].In multigroup multicast scenarios,through proper multicast precoding or beamforming design,the transmitter can form multiple narrow beams pointing to different groups by exploiting the spatial multiplexing gain and spatial diversity gain introduced by multi-antenna.The essential in precoding design is how to suppress the co-spectrum inter-group interference effectively.To this end,interference neglecting (IN),successive interference cancellation (SIC),or other interference management techniques have been adopted in multiple access schemes according to user channel conditions.To be specific,in space division multiple access(SDMA) systems,IN is used by treating all interference as noise,and the spatial multiplexing gain is exploited to support parallel transmission of multiple streams.This scheme is suitable to underloaded networks.Under the overloaded or massive connectivity cases where the antenna-number of the transmitter is insufficient,it can not neutralize all the intergroup interference and thereby resulting in saturating in rate performance.To support massive connectivity,non-orthogonal multiple access (NOMA) is proposed to transmit multiple streams across the same resource block with different power levels [7-9].Its main idea is to exploit SIC at the receivers to decode the strong interference and intended stream sequentially.Compared to SDMA,NOMA actually degrades into single-beam transmission,resulting in all annihilated spatial multiplexing gains[10].That is to say,although NOMA can avoid rate performance saturating,it suffers from a spatial degree of freedom(DoF)loss in multi-antenna systems.To tackle this issue,Clerckxet al.proposed a generalized interference management strategy,namely rate-splitting multiple access (RSMA),which exploits partial gains achieved through spatial multiplexing while maintaining a nonsaturating performance through power-domain multiplexing [10-14].Through rate or interference splitting design,i.e.,decoding part of the interference and treating the remaining part as noise,RSMA can flexibly manage inter-group interference and is deemed as a unifying interference management strategy.
In RSMA-based multigroup multicast communications,the message for each group is split into one common part and one private part at the transmitter.All the common parts are encoded into one common stream while the private parts are encoded into individual private streams,respectively.At the receiver,the common stream and its intended private stream are sequentially decoded using SIC.Existing works have demonstrated that through joint design of message(or rate) splitting and beamforming,RSMA can efficiently cope with a wide range of propagation conditions and achieve a significant system performance improvement in multigroup multicast networks[10,15-17].For instance,the authors in [15,16] proposed a rate-splitting transmission scheme for multigroup multicasting.Joudeh and Clerckx proposed a ratesplitting and beamforming strategy to achieve maxmin fairness (MMF) amongst co-channel multicast groups and demonstrated its superiority through DoF analysis[10].Furthermore,Yin and Clerckx extended[10]to the case with imperfect channel state information at the transmitter(CSIT)and demonstrated the superiority of RSMA multigroup multicast for both underloaded and overloaded scenarios[17].
All the above schemes such as SDMA,NOMA and RSMA,are considered as passive channel-adaptive mechanisms,among which RSMA is the most adaptive one.In multigroup multicast scenarios,as there exists large difference of channel quality in the same multicast group,the multicast group-rate is often limited by the user with the worst channel quality,which restricts the further improvement of the spectrum efficiency and energy efficiency.To break through the rate-limitation bottleneck,an active channel-changing strategy,namely reconfigurable intelligent surface(RIS),has been proposed recently as a green and costeffective technology to assist wireless communications[18-21].A RIS is implemented as a planar array consisting of a large number of reconfigurable passive elements which can reflect incident signals by controlling their amplitude and/or phase shift [22].Different from other existing cooperative technologies such as amplify-and-forward (AF) relay,RIS operates in full-duplex mode and reflects the received signals as a passive array without the need of any transmit radiofrequency chains[23].Due to these significant characteristics,RIS has been adopted to actively enhance the communication system performance.For instance,Yeet al.[24]adopted RIS to minimize the symbol error rate.Guoet al.[25] proposed a differential modulation scheme with the help of RIS.Wu and Zhang proposed a joint active and passive beamforming scheme for a RIS-aided communication system[22].Without CSI acquisition,the authors in [26] proposed a novel random passive beamforming scheme where RIS performs independent random reflection.While Huet al.[27]proposed a novel phase shift beam training algorithm in a multicast system with RIS-based transmitter.More applications and design aspects of RIS in the future wireless networks can be found in[28].
In RIS-aided multigroup multicast systems,through joint design of precoding matrix at the transmitter and reflection coefficients at the RIS,the equivalent link channels can be adjusted both in phase and amplitude to suppress inter-group interference efficiently.In[29],the precoding matrix at the transmitter and the reflection coefficients at the RIS were designed to maximize the sum rate of all the multicast groups.Two efficient algorithms based on majorization-minimization were proposed to tackle the non-convex problem.To minimize the transmit power,Liet al.investigated the beamforming and phase shifting problem and developed an efficient alternative algorithm with matrix lifting to decouple the optimization variables[30].To support massive connectivity and enhance channel link quality simultaneously,[31]studied RIS-assisted non-orthogonal unicast and multicast simultaneous transmission systems and jointly designed phase-shift matrix as well as unicast and multicast beamformers to minimize the transmit power.The performance gain of RIS-NOMA scheme comes from the introduced desirable channel differences among NOMA users through adjusting the reflection coefficients of RIS.
Since RSMA is the most passive channel-adaptive mechanism,while RIS can actively change the wireless channel or enhance the link quality,this arouses a question that whether the combination of RIS and RSMA can bring in excellent performance gain.To explore this question,Yanget al.studied the joint design of the transmit beamforming,rate splitting and phase shifts to maximize the energy efficiency of multi-user unicast systems in[32].The simulation results revealed that RIS-RSMA scheme has more flexible designs and can achieve higher energy efficiency than RIS-NOMA scheme.As far as we know,research on RIS-RSMA scheme is still scarce,especially in multigroup multicast systems.And in such a scenario,there not only exist complex inter-group interference,multicast group-rate limitation issue,but also exists user-unfairness issue.How to design an efficient strategy to effectively suppress inter-group interference while guaranteeing user-fairness becomes an essential issue and remains unexplored as far as we know.In this work,we aim to explore the capability of RIS-RSMA in providing fair and high-quality user service in multigroup multicast scenarios.
1.1 Our Work and Contributions
With the aforementioned objective,in this work we propose a max-min fair RIS-aided rate-splitting multiple access scheme(MMF-RIS-RSMA)for multigroup multicast communications.The main contributions of this work can be summarized as follows.
• We focus on providing fair and high-quality user service for multigroup multicast communications.By exploiting the idea of flexible interference splitting and active signal reflection,we propose a MMF-RIS-RSMA scheme to maximize the minimum group-rate.Under the constraints of given transmit power,rate splitting and unit-modulus,the beamformers and rate splitting vector at the transmitter,as well as the phase shifts at RIS are jointly designed and optimized.
• To solve the formulated non-convex problem,an alternative algorithm is proposed to optimize the beamforming,rate splitting and phase shifts iteratively.The beamforming and rate splitting optimization subproblem is solved by using the successive convex approximation (SCA) techniques.The phase shift optimization subproblem is solved through a penalty function method to achieve a rank-one locally optimal solution.
• Comprehensive comparisons are made,which reveal that the proposed MMF-RIS-RSMA scheme can obtain significant performance gain in terms of the minimum group-rate compared with the other schemes (such as MMF-RIS-NOMA scheme,MMF-RIS-SDMA scheme,etc).
1.2 Organization
The remainder of this paper is organized as follows.Section II introduces the system model,problem formulation and reformulation.The alternative algorithm based on SCA and penalty function method is presented in Section III.In Section IV,simulation results and analysis are done.Finally,Section V concludes the whole paper.
1.3 Notations
In this paper,vectors and matrices are denoted by boldface lowercase and uppercase letters,respectively.CN×1represents theN-dimensional complex vector space.(·)Tand(·)†denote the transpose operator and complex conjugate transpose operator,respectively.∅represents an empty set.CN(a,B)represents the circularly symmetric complex Gaussian random distribution with mean a and varianceB.A0 denotes a positive semidefinite matrix.E[·] means expectation.The absolute value of a scalar is denoted by|·|,and thel2-norm of a vector is denoted by||·||.INdenotes aN ×Nidentity matrix.tr(·)and rank(·)denote the trace and rank operator,respectively.Re(·)is the real part of a complex number.diag(·)stands for a diagonal matrix of vector.
II.SYSTEM MODEL AND PROBLEM FORMULATION
2.1 System Model
We consider a RIS-aided downlink multigroup multicast system as shown in Figure 1.There is anM-antenna transmitter servingKsingle-antenna receivers which are grouped intoLmulticast groups.To help the downlink transmission,a RIS equipped withNelements acts as a cooperator to reflect the signals.For clear denotation,we useK={1,2,···,K}to denote the set of all users,L={1,2,···,L}to represent the group index set,Glto stand for the set of users in thel-th group.Based on these denotations,we haveandGl ∩Gl′=∅,.We assume that receivers belonging to the same group request the same message,i.e.,all receivers in thel-th group request messageWl,l ∈L.
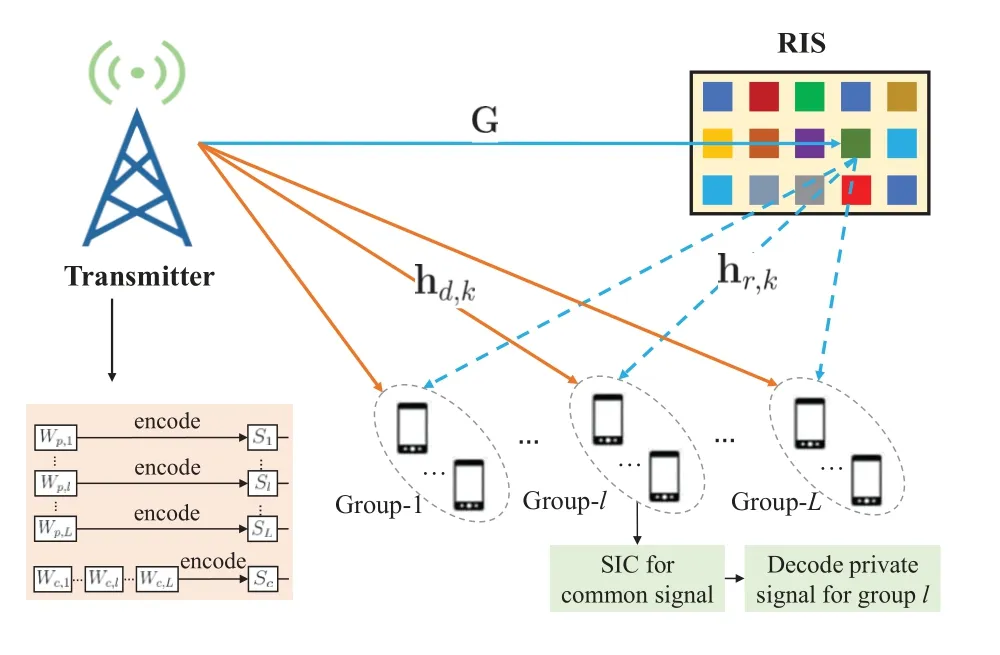
Figure 1. System model of RIS-aided RSMA multigroup multicast.
During the downlink transmission,RSMA [11-13]is adopted.At the transmitter,messageWlfor users inGlis split into a common partWc,land a private partWp,l,l ∈L.The common parts{Wc,1,Wc,2,...,Wc,L}are jointly encoded into a common streamscintended for all groups.The private partWp,lis encoded into streamslintended for receivers inGl,l ∈L[14,33].All the streamsscand{sl}are launched with normalized power,i.e.,E[|sc|2]=E[|sl|2].Then,the signal vector,s,to be sent by the transmitter can be generated by superimposing all of them together with different power levels as
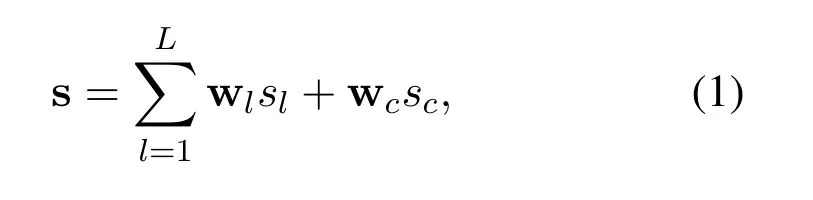
where wc ∈CM×1and wl ∈CM×1are the corresponding beamforming vectors for the common and private messages,respectively.We assume the maximum average transmit power isPmaxand we have
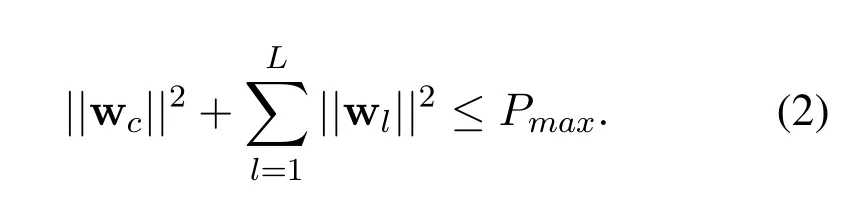
As it is shown in Figure 1,the RIS reflects the signal launched from the transmitter to the receivers.The reflection coefficient matrix is denoted as Φ=diag(β1ejθ1,β2ejθ2,...,βNejθN)∈CN×Nwithθn ∈[0,2π).For simplicity,we assumeβn=1 for alln ∈N.We defineµ(k) to denote the group index of userk,then its desired signal issµ(k).At userk,the received signal can be expressed as
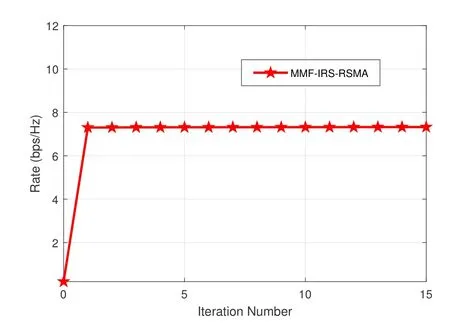
Figure 2. Convergence performance of the proposed alternative algorithm in a fully-overloaded network,where K=6,L=3,M=N=4,SNR=20 dB.
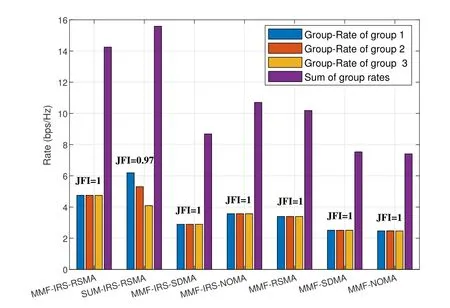
Figure 3. The group-rate of the seven schemes in a fullyoverloaded network,where K=6,L=3,M= N=4,SNR=20 dB.

2.2 Problem Formulation
In this work,our objective is to provide fair and highquality user service among co-channel users through exploring the capability of RIS-RSMA.To achieve this goal,we formulate an optimization problem to maximize the minimum achievable user rate.
Since the common streamscis broadcast to and decoded by all the users,the achievable data rate of the common stream,Rcis actually limited by the minimum common rate among users,i.e.,
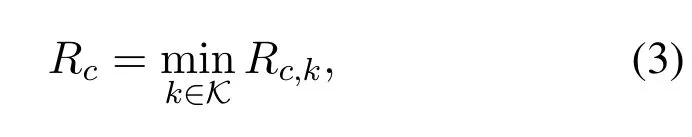
whereRc,kdenotes the achievable rate when decoding common streamscat userk.Note that in groupGl,only the portion of common rate,Rcis intended for the users ofGl,where|W|denotes the length of messageW.For easy denotation,we defineRcas the common data rate for groupGl,which satisfeisThe private streamslis multicast to and decoded by all users inGl,the achievable data rate of the private stream for groupGlis limited by mini∈Gl Rp,i,whereRp,iis the achievable rate of useri ∈Glwhen receiving the private streamsl.
From the above analysis,we know that the achievable data rates of the users in the same group are identical,and we define this rate as group-rate.In groupGl,the group-rateconsists of its intended common stream ratecland the private stream rate,i.e.,
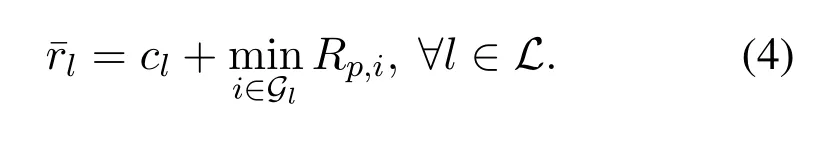
When detecting,userkfirst decodes the common streamscby treating all the private streams{sl},l ∈Las noise.According to Shannon theory,the achievable rate when decodingscat userkcan be expressed as

is the corresponding signal to interference plus noise ratio(SINR)ofscat userk.RecallingEq.(3)can be rewritten as
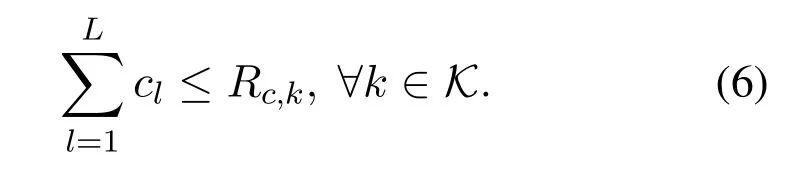
Oncescis successfully decoded and removed fromykat userk ∈K,the desired private streamsµ(k)can be decoded by treating the other private streamssj,(k) as noise.Similarly,according to the Shannon theory,the achievable rate of decoding private streamsµ(k)at userkcan be written as

represents the SINR to decode intended private streamsµ(k)at userk.
As the objective is to maximize the minimum user rate (i.e.,group-rate) under the transmit power constraint in(2),the common rate splitting constraints in(6) and the unit-modulus constraints,the beamformers wc,{wl}and rate splitting vector(or common rate vector) c=[c1,c2,...,cL] at the transmitter,as well as the phase shifts at RIS Φ are jointly designed to manage the inter-group interference efficiently.The optimization problem is formulated as

It is computationally intractable to find the global optimal solution for problem (8)due to the non-convex objective function and constraint in (6) where variables wc,{wl}and Φ are coupled with each other.
By introducing auxiliary variablestand r=[r1,...,rL],(8) can be equivalently transformed into
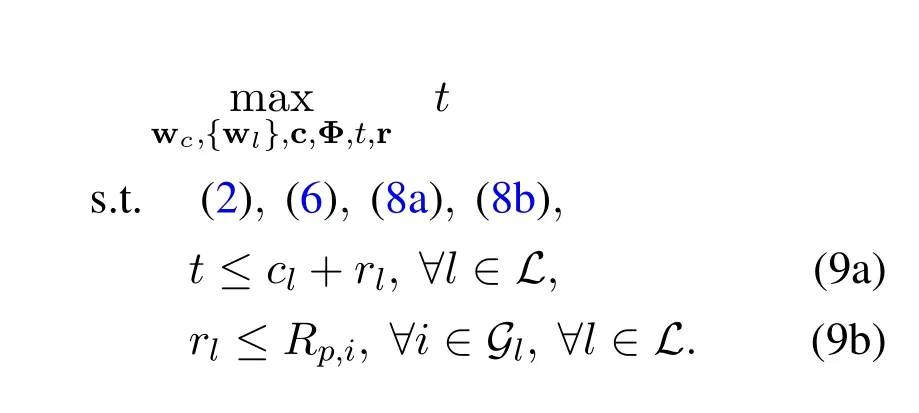
The transformed problem is still non-convex due to the non-convex constraints.In the next section,an alternative algorithm based on SCA and penalty function methods are introduced to solve the problem (9)in an iterative way.
III.PROPOSED ALTERNATE ALGORITHM BASED ON SCA AND PENALTY FUNCTION METHODS
In this section,we will first optimize the beamformers and rate splitting as well as auxiliary variables for given phase shifts at RIS based on SCA method.Then,based on the obtained variables,the phase shift is optimized with penalty function method.This alternative algorithm executes until convergence.
3.1 Beamforming and Rate-Splitting Design Based on SCA
Given a phase shift Φ,the overall downlink channel to userk,is fixed at a given time slot.The joint beamforming and rate splitting optimization problem is expressed as
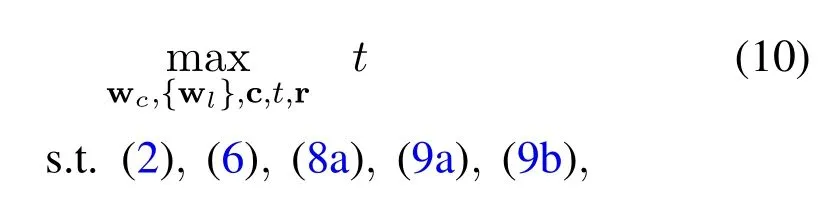
which is non-convex,since constraints (6) and (9b)are non-convex.To transform the constraints into more tractable ones,we introduce a auxiliary variable vectorα=[α1,...,αk,...,αK]Twhose elementαkrepresents the sum of interference and noise of the private signal at userk.Then the constraint (9b),i.e.,

Similarly,by introducing vectorδ=[δ1,...,δk,...,δK]Twhose elementδkrepresents the rate of the common stream at userk,and vectorq=[q1,...,qk,...,qK]Twhose elementqkrepresents the interference plus noise of the common signal at userk,constraint (6),i.e.,

can be equivalently transformed to the following three inequalities:
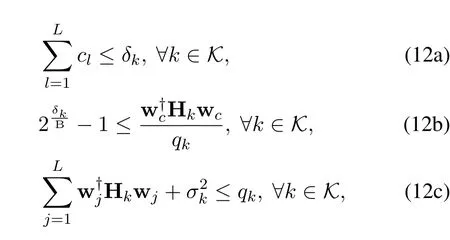
where (12a) and (12c) are convex constraints while(12b)is not.
Focusing on the non-convex constraints (11a) and(12b),there exists a quadratic-over-linear termwhich is jointly convex in variables{w,y}given H a Hermitian positive semidefinite matrix[35,36].So,we can get that both sides of the inequalities in (11a)and (12b)are convex and can be treated as the difference of convex (DC) form [37].Therefore,problem(10) can be equivalently transformed into the following non-convex DC programming:
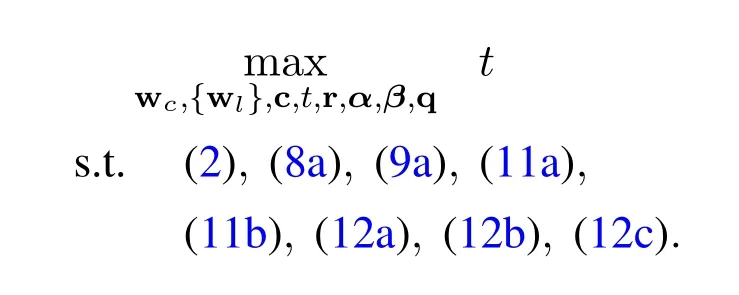
To solve it,we adopt the SCA-based algorithm to achieve a local minimum solution iteratively.To be specific,the termis approximated by using the first-order lower approximation at point{w(j),y(j)}in thej-th iteration[38]
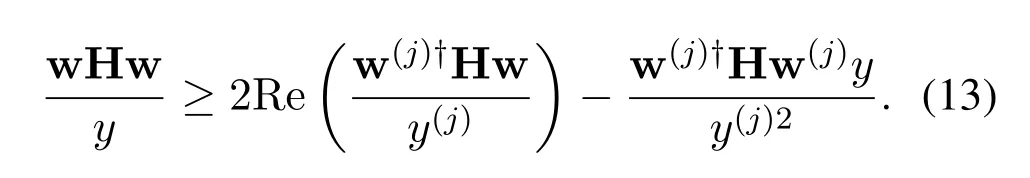
Thus (11a)and (12b)can be approximated as

respectively.Obviously,these functions are all affine.
For easy denotation,we define a column variable vector,cT,t,rT,αT,βT,qT]T.Based on the preliminaries above,the original optimization problem can be approximated to a convex optimization problem in thej-th iteration as follows

This is a standard convex optimization problem,thus can be solved by using the interior point method provided by CVX toolbox [35].The obtained solution will be seen as the updated feasible point in the next iteration.Such iteration process goes until it converges to a local minimum.Note that the convergence of the process and the local optimality of the obtained solution can be guaranteed[36,39].Algorithm 1 summarizes the detailed procedure of the proposed algorithm.

3.2 Phase Shift Design Based on Penalty Function Method
Given the beamforming wc,{wl}and common rate splitting c,problem (9) is reduced to a feasibilitycheck problem of finding phase shift Φ.Letϕ=[ejθ1,ejθ2,...,ejθN]†,we have

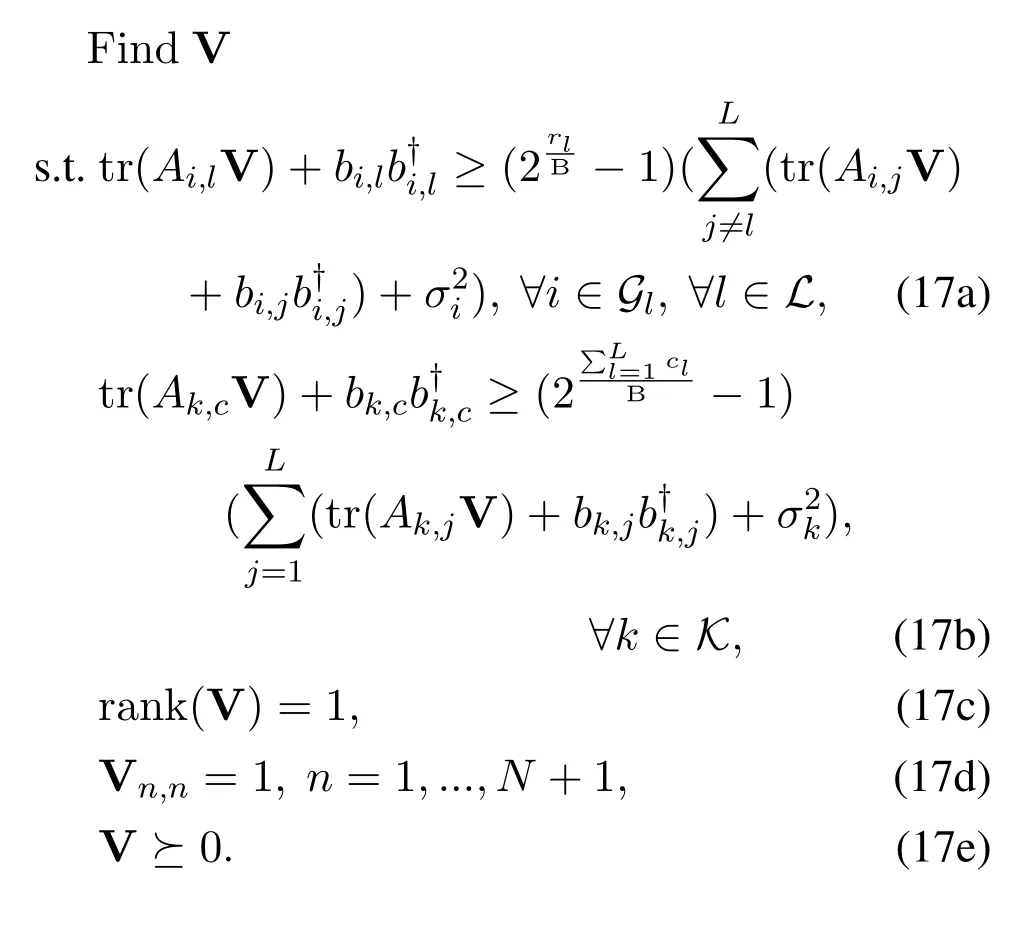
According to [22],we can further transform problem(17)into an optimization problem with an explicit objective in the following,which can help achieve better converged solution.
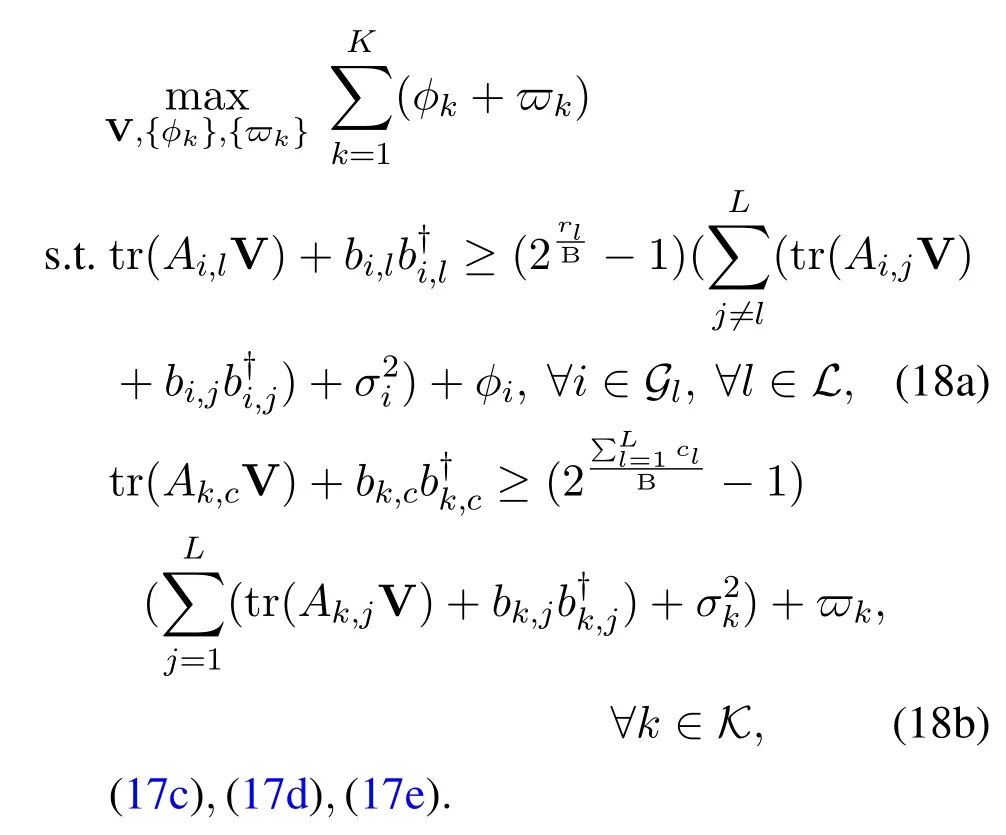
According to [8,40],the rank-one constraint (17c)in problem(18)can be transformed into the following equivalent reverse convex constraint,
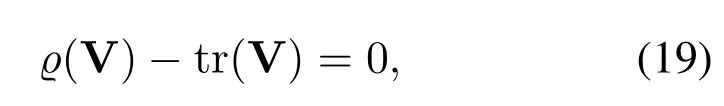
whereϱ(V)is the maximal eigenvalue of V.Eq.(19)impliesϱ(V)=tr(V).Thus it is possible to requirewhere vmaxis the unitnorm eigenvector of V corresponding toϱ(V).We knowϱ(V)-tr(V)≤0 always holds.To makeϱ(V)-tr(V) as great as possible,we adopt the penalty function method to augment the objective function as,whereς >0 denotes the penalty factor.Then,the rankone constrained SDP programming(18)can be further transformed into the following
where all the constraints are convex.The objective function is in the form of DC,which can be approximated by using the first-order lower approximationV(j)))+tr(V)]}at point{V(j)}in thej-th iteration[38].Based on the preliminaries above,the original optimization problem can be approximated as a convex optimization problem in thej-th iteration,
This is a standard convex optimization problem,and can be solved by CVX toolbox [35].The rank-one locally optimal solution can be achieved through iterative computation.For better illustration,the detailed procedure of the proposed penalty function algorithm is summarized in Algorithm 2.

Note that the whole proposed alternative algorithm includes Algorithm 1 and Algorithm 2.In one external iteration,the objective function is maximized and finally converges to a local minimum through executing Algorithm 1.Then in Algorithm 2,the value of objective function,beamformers and rate splitting vector are fixed,a better feasible phase shift matrix is searched.The solution obtained from the two algorithms is also a feasible solution in the next iteration.Hence,the alternative algorithm can guarantee convergence.
3.3 Complexity Analysis
The total complexity of the proposed alternative algorithm comes from two parts,Algorithm 1 and Algorithm 2.At each iteration of the proposed alternative algorithm,problem(16)as well as(21)are solved separately.To be specific,the complexity of Algorithm (1) solving the nonlinear convex problem (16)is
whereϵ1denotes the the given solution accuracy,I1denotes the number of iterations before convergence,and (M+LM+2L+3K) represents the number of variables[41-44].The complexity of Algorithm 2 solving the SDP problem(21)is
where(N+1)denotes the dimension of the semidefinite cone andI2represents the number of iterations for Algorithm 2 to converge.To conclude,the aggregate complexity of the proposed alternative algorithm is
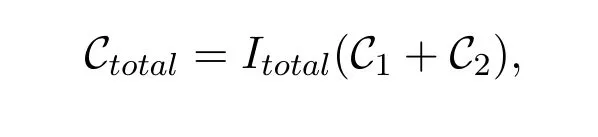
whereItotalstands for the total number of iterations executing the alternative algorithm.
IV.SIMULATION RESULTS AND ANALYSIS
In this section,simulations are carried out to evaluate the performance of the proposed MMF-RIS-RSMA scheme.For comparison purpose,six similar transmission schemes are simulated and included as benchmarks,the details are shown in the following.
• MMF-RIS-SDMA: It aims to provide fairness among users by adopting RIS-SDMA.The beamforming and phase shift are optimized to maximize the minimum group-rate.The adopted algorithm can be simplified from our proposed algorithm by settingcl=0,l ∈L.The users decode their signal by treating all interference as noise;
• MMF-RIS-NOMA: It aims to provide fairness among users by adopting RIS-NOMA.The beamforming,phase shift and decoding order are optimized to maximize the minimum group-rate.The receivers decode their intended signal via SIC;
• MMF-RSMA: It aims to provide fairness among users by adopting RSMA [10],the beamforming and rate-splitting are jointly optimized without phase shift optimization;
• MMF-SDMA: It aims to provide fairness among users by adopting SDMA.The beamforming is optimized to maximize the minimum group-rate and there is no RIS assisting;
• MMF-NOMA:It aims to provide fairness among users by adopting NOMA.The beamforming is optimized to maximize the minimum group-rate and there is no RIS assisting;
• SUM-RIS-RSMA: It aims to maximize the sumrate of all users by adopting RIS-RSMA.The beamforming,phase shift and rate-splitting are jointly optimized to maximize the sum-rate;
In all the following simulations,the system setup of all the schemes is the same.Recall that the achievable data rates of the users in the same group are identical,i.e.,group-rate.In the following the convergence of performance and the group-rate fairness performance is first evaluated.And then,the simulations of the minimum group rates for different transmit SNR,different number of the transmitter antennas and different number of the RIS elements are investigated,respectively.Finally the effects of user channel correlation and channel strength disparity on system performance are also investigated.
4.1 Convergence Performance
To evaluate the convergence performance of the proposed algorithm,we set the total number of users to beK=6,and the 6 users are divided intoL=3 groups with two users in a group.The number of the transmitter antennas and the number of RIS elements are set to beM=N=4.All the channels are assumed to follow both large-scale pass loss fading and small-scale Rayleigh fading.For simplicity,all the transceiver distances are assumed to be identical and normalized.The Rayleigh fading channels follow independent and identically distributed (i.i.d.) complex Gaussian distribution,i.e.,hd,k~CN(0,IM),hr,k~CN(0,IN),G~CN(0,IN×M).The convergence performance of the proposed algorithm for MMF-RIS-RSMA scheme is evaluated.The simulation results are averaged over 100 independent channel realizations,as illustrated in Figure 2.We observe that the minimum group-rate converges to a stationary point after several iterations,which confirms the theoretical analysis.
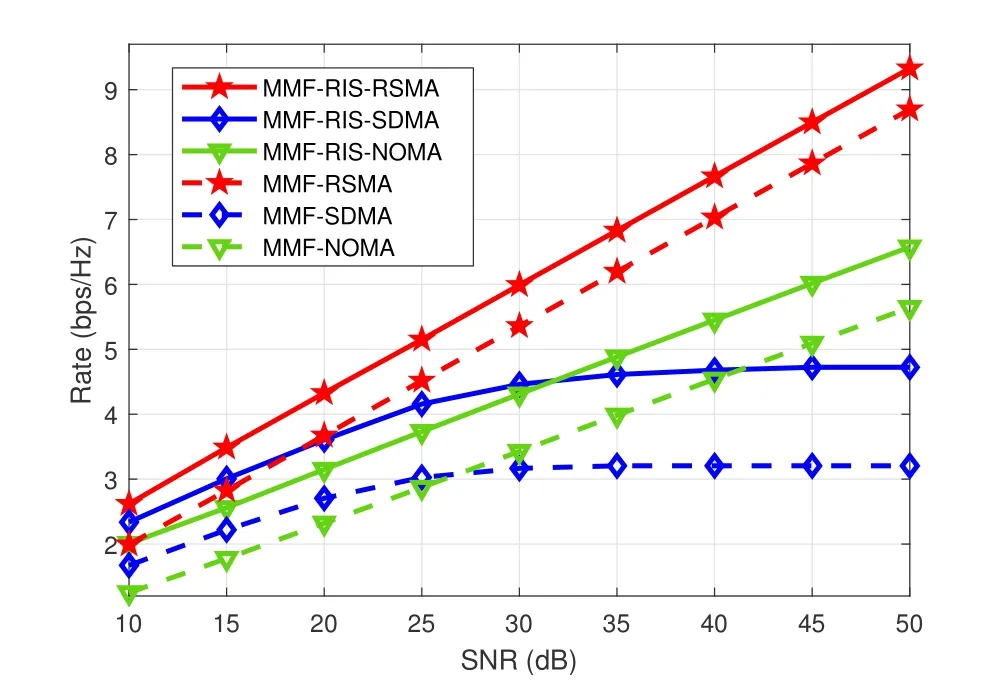
Figure 4. The minimum group-rate performance versus the transmit SNR in a fully-overloaded network,where K=6,L=3,M=N=4.
4.2 Group-Rate Fairness Performance
To evaluate the rate fairness performance of the proposed scheme,the group-rate is investigated in a overloaded network.To measure the rate fairness achieved by different schemes,the Jain’s fairness index(JFI)is adopted [45].It is defined asfor a nonnegative real vector,where 0≤JFI≤1,and a higher JFI indicates better fairness.
By settingK=6,L=3,andM=N=4,we investigate the group-rate fairness performance of all schemes.Similar to Subsection 4.1,the Rayleigh fading channels are hd,k~ CN(0,IM),hr,k~CN(0,IN),G~CN(0,IN×M).For the same system setups,simulations of all the seven schemes are done.The obtained group-rate distribution and fairness of all schemes are illustrated in Figure 3.Results indicate that the proposed MMF-RIS-RSMA scheme performs worse than SUM-RIS-RSMA in terms of sum group rates,but it offers better fairness among groups(JFI=1).In addition,we find that the JFI achieved by the other five MMF-related schemes is also 1,but their minimum group-rate and the sum group-rate are less than the counterparts of MMF-RIS-RSMA.
Since SUM-RIS-RSMA can not provide good rate fairness among users or groups,the simulations of the minimum group-rate for this scheme is no longer included in the following subsections.
4.3 Minimum Group-Rate Versus SNR
By settingK=6,L=3,andM=N=4,we investigate the minimum group-rate performance for different transmit SNR.Similar to Subsection 4.1,the Rayleigh fading channels are hd,k~CN(0,IM),hr,k~ CN(0,IN),G~ CN(0,IN×M).All the simulations of the six schemes are carried out under the same system setups.In Figure 4,we can see that the three RIS-aided schemes,i.e.,MMF-RISRSMA,MMF-RIS-SDMA and MMF-RIS-NOMA,outperform their corresponding schemes without RIS assisting.This is because with RIS the wireless transmission channel is strengthened.Among the three RIS-aided schemes,the rate of MMF-RIS-SDMA saturates in high SNR regime due to the DoF limitation under the case of overloaded networks.MMFRIS-NOMA can avoid rate performance saturating issue by exploiting power-domain multiplexing gains of NOMA.But,its rate is far less than that of MMF-RISRSMA in high SNR regime.That’s because NOMA actually degrades into single-beam transmission and suffers from a spatial DoF loss in multi-antenna systems.While MMF-RIS-RSMA performs the best as RSMA exploits partial gains achieved through spatial multiplexing while maintaining a non-saturating performance through power-domain multiplexing[10].
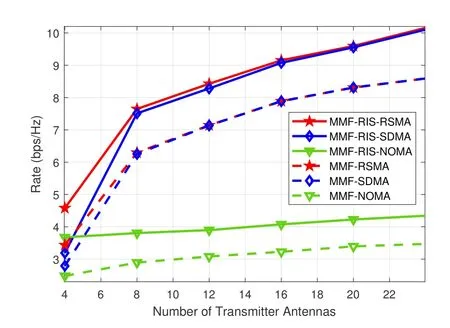
Figure 5. The minimum group-rate performance versus the antenna-number of the transmitter for K=6,L=3,N=4,SNR=20 dB.
4.4 Minimum Group-Rate Versus the Antenna-Number of the Transmitter
By settingK=6,L=3,N=4 and SNR=20 dB,we investigate the minimum group-rate performance for different antenna-number of the transmitter,M.Similar to Subsection 4.1,the Rayleigh fading channels are hd,k~CN(0,IM),hr,k~CN(0,IN),G~CN(0,IN×M).All the simulations of the six schemes are carried out under the same system setups.In Figure 5,asMincreases,the rate achieved by MMF-RISSDMA is approaching to that of MMF-RIS-RSMA,in the meanwhile the rate of MMF-SDMA is approaching to that of MMF-RSMA.The reason is that asNincreases,the network becomes underloaded and hence full DoF can be achieved by both MMF-RSMA and MMF-SDMA.In addition,we find that the rates of both MMF-RIS-NOMA and MMF-NOMA have a slight improvement asNincreases.Since NOMA degrades the spatial DoF and the improvement is only from the spatial diversity gain.
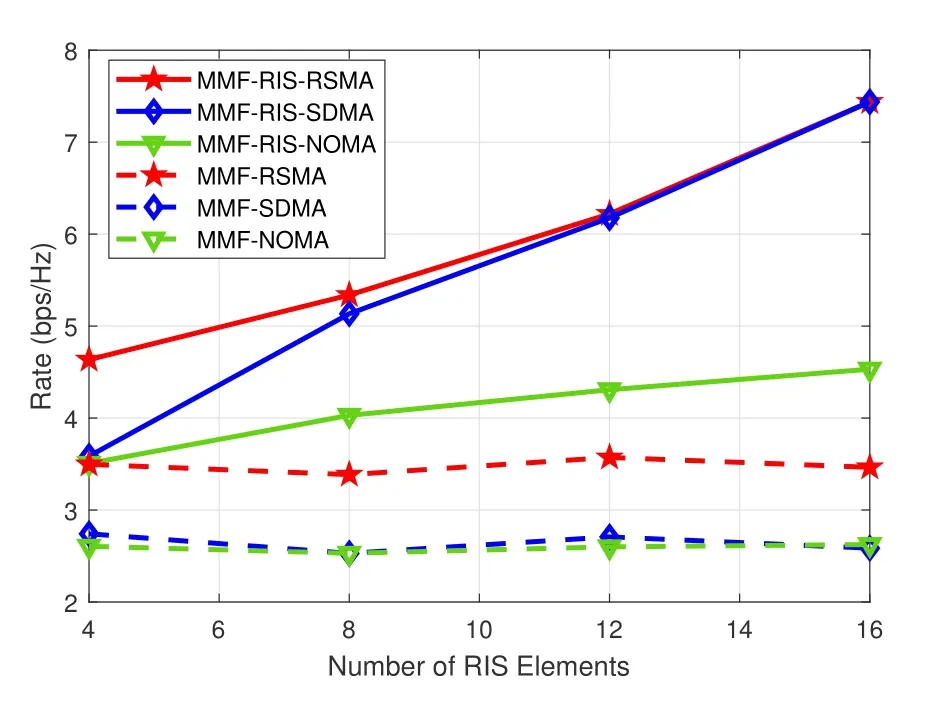
Figure 6. The minimum group-rate performance versus the number of RIS elements for K=6,L=3,M=4,SNR=20 dB.
4.5 Minimum Group-Rate Versus the Number of RIS Elements
By settingK=6,L=3,M=4 and SNR=20 dB,the minimum group-rate performance is investigated for different number of RIS elements,N.Similar to Subsection 4.1,the channels are hd,k~CN(0,IM),hr,k~CN(0,IN),G~CN(0,IN×M).From Figure 6,we observe that the rate achieved by MMF-RISSDMA is approaching to that of MMF-RIS-RSMA asNincreases.That’s because for an increasingN,RIS has growing powerful ability in changing the channel by adjusting the reflection phase to make the spatial multiplexing gain of the channel increase.AsNincreases,the rate of MMF-RIS-NOMA also increases but more slowly than MMF-RIS-RSMA and MMFRIS-SDMA.That’s because the channel strength difference among users in this simulation is not obvious,hence the performance gain of NOMA is underutilized.Note that performance of the schemes without RIS is not sensitive toN.
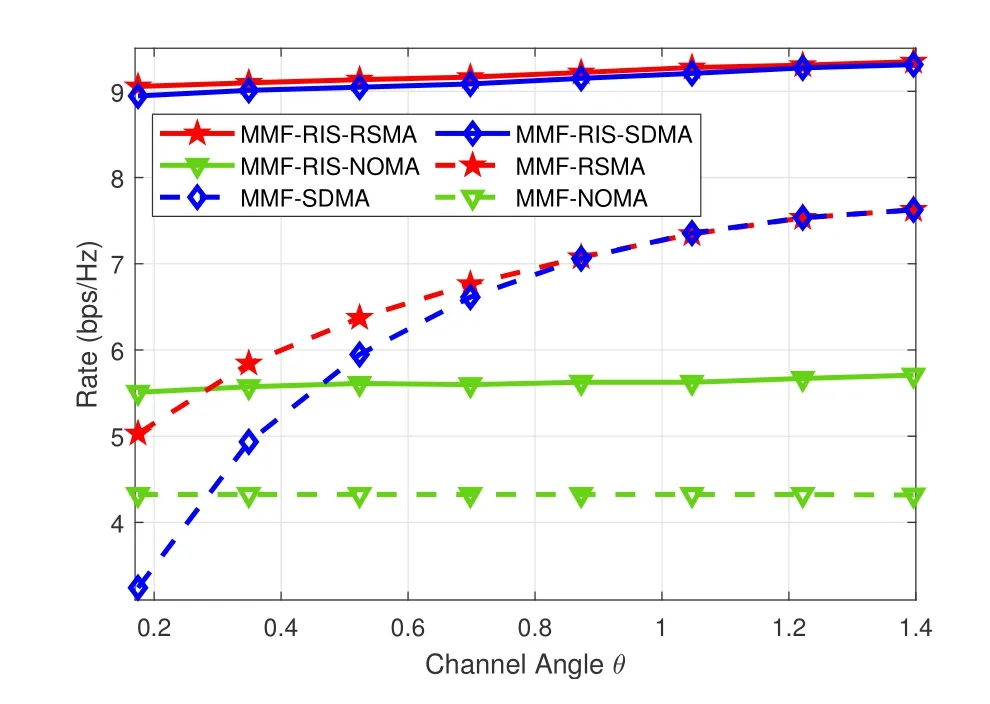
Figure 7. The minimum group-rate performance versus the channel angle disparity θ for K=2,L=2,M=N=4,SNR=20 dB,γ=1.
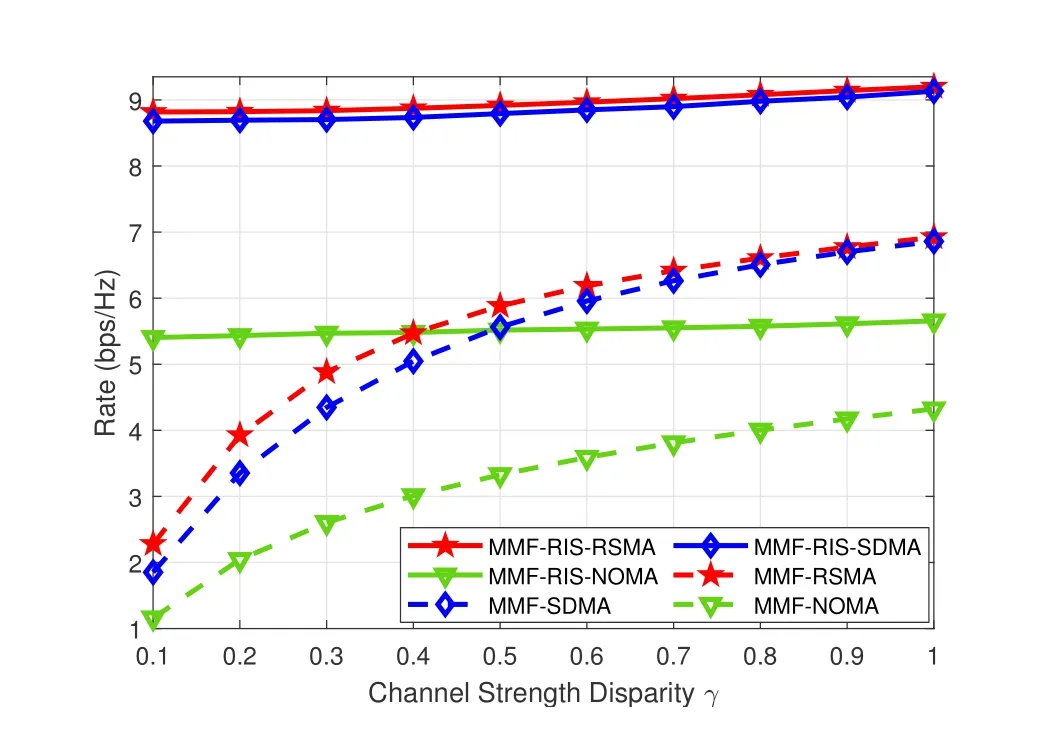
Figure 8. The minimum group-rate performance versus the channel strength disparity γ for K=2,L=2,M=N=4,SNR=20 dB,θ=π/4.
4.6 The Effects of Channel Correlation and Channel Strength Disparity on the Minimum Group-Rate
By settingK=2,L=2,M=N=4 and SNR=20 dB,the effects of channel correlation and channel strength disparity of users on the minimum group-rate are investigated in an underloaded network.We adopt the channel model in [14]where the channels are hd,1=[1,1,1,1]†,hd,2=γ[1,ejθ,ej2θ,ej3θ]†.γcontrols the channel strength disparity of the two users,andθcontrols the channel correlation or channel angle disparity.Other links are hr,k~CN(0,γ2IN),G~CN(0,IN×M).
Figure 7 illustrates the minimum group rates for different channel angleθby settingγ=1.We find that MMF-RIS-RSMA and MMF-RIS-SDMA obviously outperform the other schemes and almost keep stable asθincreases.That’s because the network is underloaded,both the two schemes can make full use of the spatial multiplexing gain through adjusting the wireless channels to be orthogonal enough via RIS.For the schemes without RIS,as the channels are non-changeable,they have to adjust the interference management strategy to adapt to the channels.With the increase ofθ,the user channels become orthogonal.Thus the rate performance of MMF-SDMA is approaching to that of MMF-RSMA for largeθ.In addition,the rate performance of both MMF-RIS-NOMA and MMF-NOMA is not sensitive toθ.
Figure 8 illustrates the minimum group rates for different channel strength disparityγby settingθ=π/4.The performance trends of all the schemes are almost the same with those in Figure 7.Note that the performance gap of MMF-RIS-NOMA and MMF-NOMA is very large whenθis small.That’s because MMFRIS-NOMA can adjust the channel environment to improve the rate performance while MMF-NOMA can only adapt to the channels.Furthermore,the performance gap of MMF-RSMA and MMF-SDMA is not too large as the user channels are orthogonal relatively.
V.CONCLUSION
In this paper,we have proposed an MMF-RIS-RSMA scheme for multigroup multicast communications to provide fair and high-quality multiuser service.The minimum rate maximization problem was formulated through jointly designing the beamformers and rate splitting at the transmitter,as well as the phase shifts at RIS.To solve the formulated non-convex problem,an alternative algorithm was proposed to decouple the original problem into two subproblems and solve them iteratively.The two subproblems were solved through SCA-based algorithm and penalty function method,respectively.Benefiting from the dual utilization of RSMA and RIS,it is shown that the proposed MMF-RIS-RSMA scheme brings significant performance gain in terms of the minimum group-rate.
ACKNOWLEDGEMENT
This work was supported in part by the Project of International Cooperation and Exchanges NSFC under Grant No.61860206005,in part by the National Natural Science Foundation of China under Grant No.62201329,No.62171262,and in part by Shandong Provincial Natural Science Foundation under Grant ZR2021YQ47.
杂志排行
China Communications的其它文章
- Coordinated Planning Transmission Tasks in Heterogeneous Space Networks: A Semi-Distributed Approach
- Secrecy Rate Maximization for 6G Cognitive Satellite-UAV Networks
- Secure Transmission in Cognitive Radio Networks Using Full-Duplex Technique with Outdated CSI
- Computation Rate Maximization in Multi-User Cooperation-Assisted Wireless-Powered Mobile Edge Computing with OFDMA
- A Novel Multi-Granularity Flexible-Grid Switching Optical-Node Architecture
- Model-Free Adaptive Frequency Calibration for Voltage-Controlled Oscillators
