基于可靠性理论的关键链缓冲区计算方法

肖勇 管致乾

(上海电力大学，上海 200082)

0 引言

在项目实施过程中，工期延误问题屡见不鲜，其主要原因在于对关键资源的管理缺乏足够的重视[1-2]。关键链项目管理 (Critical Chain Project Management，CCPM) 方法能够有效降低项目工期的不确定性影响，并缩短项目计划工期[3-4]。与传统的项目进度管理方法相比，CCPM具有三个特点[5-6]：①通过考虑人的行为学假设消除非必要的安全时间，保证安全时间不会被滥用[7]；②强调资源的可用性，能够在两个工序之间发生资源冲突时合理分配资源[8]；③通过在项目流程中插入应急缓冲区，降低项目完工的超时风险[9]。

不同的缓冲区(项目缓冲区、驳接缓冲区和资源缓冲区)在关键控制点具有不同的作用。项目缓冲区位于项目网络末端，用来保证项目完成时间免受单个任务工期变化的影响。驳接缓冲区位于交点上，用来保证非关键工序即使发生变化也不会影响关键链任务。非关键工序和关键工序之间的资源缓冲区[10]用来保护关键链免受资源不可用的影响。这些缓冲区作为警告信号，能够确保及时完成关键链上的工序所需的资源是可用的[11]。

1 理论基础

当前，经典的缓冲区计算方法是剪切粘贴法(Cut and Paste Method,C&PM)。该方法将预期活动工期的50%作为安全时间，再将安全时间之和的50%作为缓冲区，具有操作简单的优势。然而，非关键链会线性地影响缓冲区大小，导致在较长的非关键链中缓冲区相对较长且不实用。Newbold进一步完善了C&PM方法，提出了根平方误差法(RSEM)[12]。虽然该方法考虑了任务持续时间的已知变化，但可能导致工序多的关键链缓冲区不足[13]。在上述理论的基础上，Tukel和Eksioglu开发了两种方法：带密度的适应性程序(APD)和带资源紧密度的适应性程序(APRT)。前者根据进入关键链的子网络结构估算缓冲区大小，后者考虑了通往缓冲区的链上工序所需资源的稀缺性[14]。

在上述方法中，缓冲区的大小是由大于1的系数缩放的缓冲区内的路径合并的标准偏差确定的[15]。De等[16]引入熵理论衡量调度网络的复杂性，以此确定CCPM时间缓冲区大小。Zhang等[17]通过整合资源紧密度和网络复杂性模型，提出估算缓冲区大小的单一框架。王肖文等[18]认为，在实际操作中并非所有项目都存在帕金森定律中所描述的情况，不能对每个工序的安全时间进行平均化，应对每个工序的不确定性影响因素进行分析，通过加入不同属性因子，使缓冲区的设置更加科学合理[20]。同样，张静文等[19]结合时差定义和缓冲区设置原则，在设置项目缓冲区时考虑了不确定性因素对各个工序影响的不同，引入关键工序工期的影响因子。刘士新等[21]认为，在设置缓冲区时，应依据在指定资源分配方式下每个工作的自由时间分别设置缓冲区。周阳等[22]提出，在单资源约束下缓冲区的大小可采用排队论确定，通过消除整个项目实施过程中的不确定性因素，使工期和成本得以平衡。王晶[23]认为，关键链汇入缓冲区的取值具有区间性，采用自由时差法和总时差法确定汇入缓冲区的大小更符合缓冲区设置的本质；采用影响因子法确定项目缓冲区的大小更加符合实际。

虽然上述研究将不同的项目属性纳入缓冲区大小的考量，但没有考虑项目进度中资源获取的随机效应。基于此，本文提出一种嵌入可靠性理论的缓冲区设置方法，以解决项目进度管理中资源可用的随机性问题。

2 缓冲区设置方法

2.1 基于资源的可靠性

本文在计算缓冲区大小时，进行以下假设：

(1)资源在有限的供应条件下，项目进度受到资源制约。

(2)分配给工序的资源可靠性值在工序执行期间保持不变。

(3)同一类型的所有资源具有相同的可靠性值。

(4)资源在统计上是独立的，即某一特定资源的可用性并不影响其他资源的可用性。

将工序i的资源结构功能定义为一个模型，分配给工序i的每种资源的状态用随机变量Xij表示。如果资源可用，则Xij=1；否则，Xij=0。根据以下二元函数公式评估每种工序在所需资源方面的状态(资源结构功能)，即

θ(Xi1,Xi2,…,XiN)=

(1)

考虑到每个工序的资源结构函数，计算工序i的基于资源的可靠性Ri。Ri被定义为完成工序i所需资源的可用概率。事实上，它是资源结构函数等于1的概率。公式如下

Ri=Pr[θ(Xi1,Xi2,…,XiN)=1]

(2)

为了完成工序i，必须在整个工序期间拥有所有的资源。即当且仅当工序i的所需的n个资源在其执行期间都可用时，工序i才能完成。资源结构函数如下

(3)

若每个Xij=1，则θ(Xi1,Xi2,…,XiN)=1。或者说，任何一个资源的不可用性都会导致工序延时。因此，Ri可以用资源可靠性的乘积表示，公式如下

(4)

式中，Ri是工序i整体基于资源的可靠性；rij是工序i对分配给该工序的资源类型j的可靠性。

此外，式(4)成立的条件是假设只有一个单位的资源j是可用的，同时需要一个单位的这种资源来完成工序i。然而，在实践中，对于某些工序而言，资源的可用量可能高于对该资源的需求量，因此，nij>kij。其中，nij和kij分别是分配给工序i的资源类型j的可用单位和所需单位的数量。在这种情况下，如果nij个资源中至少有kij个可用于执行工序，那么工序i就可以进行。或者，如果所需资源中的kij或更多的nij资源不可用，则工序i将被延迟。假设所有j类型的可用资源具有相同的可靠性rij，那么j类型的nij个资源中的kij的可靠性r(kij/nij)可以通过以下公式计算，即

(5)

对于一个需要分配N种不同类型资源的工序，式(5)可以扩展为

(6)

需要注意的是，当nij=kij=1时，式(6)可以简化为式(4)。式(6)中表示的分配给项目工序的多种资源的总体可靠性的概念可以通过逻辑图表示，即资源可靠性框图(RBD[R])，如图1所示。RBD是较为常用的可靠性图表，RBD[R]对可靠性框图(RBD)进行了改进和完善。

RBD显示了一个系统中各组成部分之间的逻辑联系，说明了系统的功能状态，给定了功能各组成部分的状态，能够直观地分析项目工序所需资源的总体可靠性，并考虑到每个单独资源的可靠性[25]。RBD[R]中的矩形表示一个工序所需的资源，线条表示资源之间的关系。RBD[R]直观地展示了如何将资源分配给一个工序，以便在其目标结束日期内完成该工序。

2.2 基于资源可靠性的缓冲区估算

综上所述，本文将项目工序的资源可靠性进行量化，将数值设定为一个比例系数以调整时间缓冲区大小。换言之，缓冲区的大小是在一个关键链采用RSEM算法后所得到的数值上分配一个由各个工序可用资源的可靠性函数构成的比例系数确定的。

(7)

对工序持续时间采用悲观和乐观估计。如果T是工序i的悲观工期，则与90%的估计置信度有关；如果T是工序i的乐观工期，则与50%的置信度有关。考虑到Ri的工序资源的不可靠性，假设工序完成时间为对数正态分布，将有m个工序的驳接关键链的缓冲区大小定义为BSR，公式如下

(8)

通过用资源可靠性代替资源不可靠性，公式如下

(9)

由此可见，资源可靠性值是从一个常量中减去的，这意味着缓冲区的大小随着资源可靠性的降低而增加。显然，若Ri=1，则比例因子(2-Ri)对BSR没有影响，故式(9)等同于根平方误差法。

3 实例应用

3.1 案例概况

某项目关键链网络图如图2所示，包含10项工序和8项资源。矩形方框表示工序，箭头表示工序执行顺序。该网络包含一个关键链(A→E→H→J)和两个非关键链。非关键链B→C→D→F与关键链上的工序H接驳，非关键链G→I通过工序J与关键链接驳。在工序J和项目到期日之间的项目网络末端增加一个项目缓冲区(PB)。为了确保非关键链B→C→D→F中的任何变化不会影响关键链上的工序H，在工序I和J之间增加缓冲区FB2。其中，非关键链G→I和关键链A→E→H→J在J工序处进行接驳。

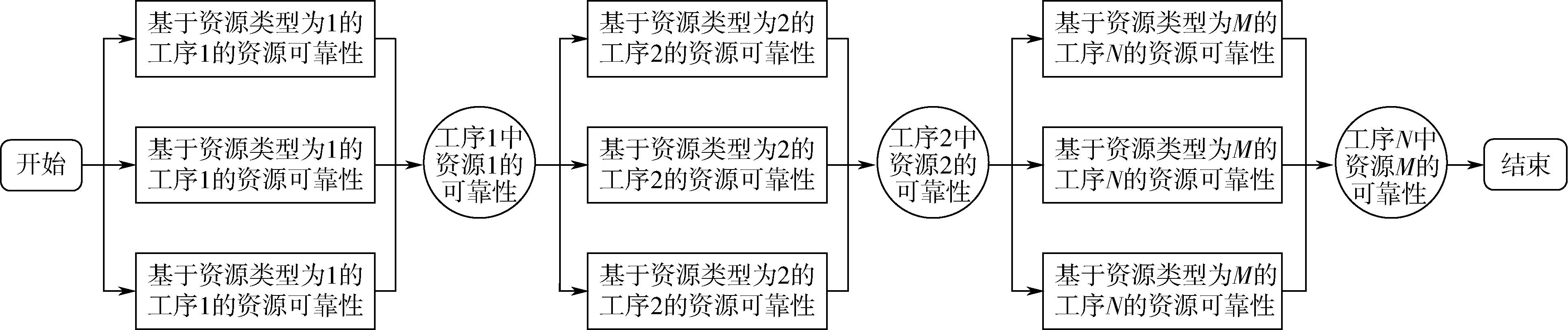
图1 资源可靠性框图(RBD[R])

图2 某项目关键链网络图

3.2 结果分析

对工序A和工序B的计算过程进行分析。首先，完成这项工序所需的资源被映射成RBD。工序A和工序B的RBD被表示为其所需资源(4、6和1、2)的系统，以及由该资源所有可用单元的平行组合构成的每个资源的功能块，如图3所示。

首先，计算工序A和工序B网络中每个工序的rij值。资源类型为4的可靠性是通过计算该资源的4个单位中至少有3个单位被分配给工序A的概率进行估计，公式如下

同理，得到

rA6=0.902 5

rB1=0.995 3

rB2=0.996 4

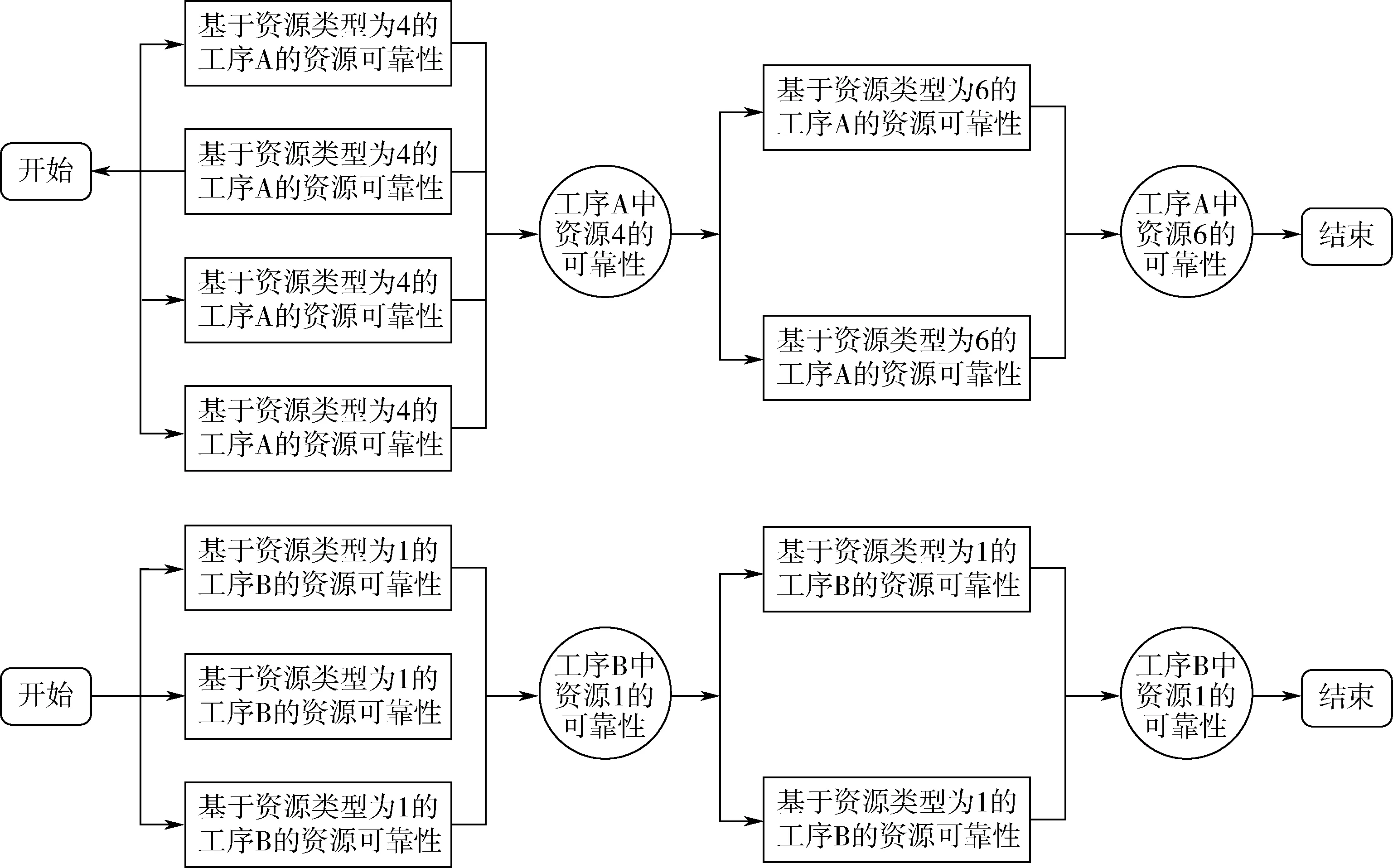
图3 工序A和工序B的RBD

其次，估计工序J的整体资源可靠性，即2、4、5、8类资源都可用的概率。计算公式如下

RA=0.999 9×0.902 5=0.902 4

RB=0.995 328×0.996 4=0.991 7

同理，计算其他项目工序的整体资源可靠性，结果见表1。

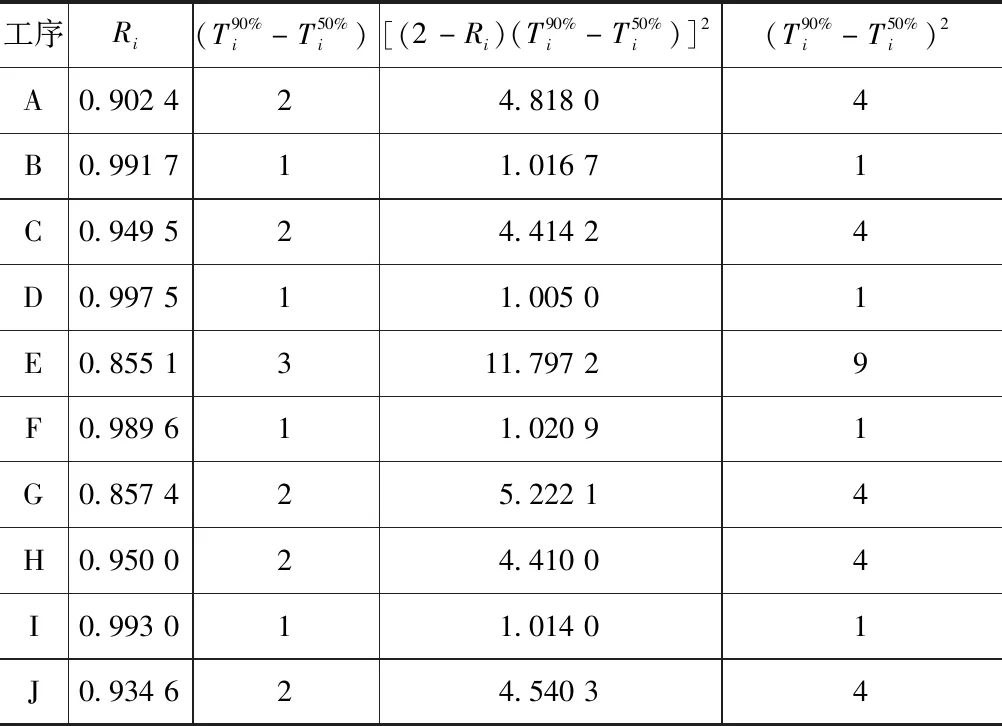
表1 其他工序关键链相关数据

利用公式计算出对应链的BSR值。关键链A→E→H→J的缓冲区计算公式如下

BSR(A→E→H→J)

=5.06

同理可得

BSR(B→C→D→F)=2.73

BSR(G→I)=2.5

最后，分别计算出对应链的BSRSEM和BSC&PM，结果如下

BSRSEM(A→E→H→J)=4.583、BSRSEM(B→C→D→F)=2.646、BSRSEM(G→I)=2.236

BSC&PM(A→E→H→J)=9、BSC&PM(B→C→D→F)=5、BSC&PM(G→I)=3

式中，BSRSEM表示平方根误差法得到的缓冲区大小；BSC&PM表示剪切粘贴方法得到的缓冲区大小。

综上所述，采用C&PM方法计算得到的关键链A→E→H→J的缓冲区为9周，远远大于通过本文方法计算得到的缓冲区5.06周，误差比例为77.8%。使用C&PM方法计算的非关键链G→I的缓冲区大小与本文方法相比，缓冲区误差比例为20%。这是因为在C&PM方法中，缓冲区的大小与工序链的长度呈线性增长，时长较长的工序链产生了较大的缓冲区[26]。

本文提出的方法与RSEM方法相比会产生更大的缓冲区。这是因为资源可靠性在式(9)中的对应比例系数大于1。在非关键链B→C→D→F中，工序的Ri值很高(0.949 5～0.991 7)，导致两种方法之间误差较小，为3.1%。在关键链A→E→H→J中，工序E的RE值相对较低，导致本文方法计算得到的缓冲区(5.06周)大于RSEM方法计算的结果(4.583周)，误差为10.4%。同样，非关键链G→I上的工序G的资源可靠性低，导致使用本文的计算方法的结果和RSEM方法计算的平均缓冲区大小误差较大，为11.8%。

4 结语

随着项目规模越来越大、项目内容越来越复杂，项目资源(物质资源和人力资源)对项目进度具有决定性影响。基于此，本文在研究项目工序资源可用性概率的基础上，结合可靠性理论改进了RSEM方法。该方法克服了C&PM和RSEM方法的不足，能够降低资源可靠性对项目进度的影响，更符合项目实际需求。通过案例验证可知，本文提出的项目关键链缓冲区计算方法与C&PM和RSEM方法相比，能够更好地解决基于C&PM方法缓冲区过大的问题。同时，弥补了项目属性的缺失，使缓冲区计算结果更加可靠，解决了基于RSEM方法缓冲区过小的问题。