改进的三电平逆变器变虚拟空间矢量调制策略

周冠卿，张国荣，解润生，王春鹏，陈伟伦

（1. 合肥工业大学电气与自动化工程学院，安徽省合肥市 230009；2. 光伏系统教育部工程研究中心（合肥工业大学），安徽省合肥市 230009）

0 引言

中点钳位型（NPC）三电平逆变器相比于传统的两电平逆变器具有输出电压谐波分量小、承压能力强等优点，因此在中高压大功率领域得到了广泛应用［1-2］。然而，NPC 三电平逆变器始终存在着中点电位失衡的问题［3］。中点电位失衡不仅会导致直流侧上下电容和开关管承压不均，还会引起输出电流谐波含量增大，开关器件寿命降低等问题［4］。

针对该问题，许多学者对其进行了研究。常见的中点电位控制方法有基于载波脉宽调制的方法［5-7］和基于空间 矢量脉宽调 制（SVPWM）的方法［8-21］，两 类 方 法 在 一 定 条 件 下 相 互 等 效［22］。SVPWM 方法由于其控制简单以及较高的电压利用率，得到了广泛应用。文献［8］基于SVPWM，在冗余小矢量中引入平衡因子，可以有效控制中点电位。文献［9］根据补偿电荷能力强弱对冗余小矢量进行选择并引入平衡因子，进一步提高了中点平衡能力。文献［10］采用一种简化的脉宽调制（PWM）策略，根据三相基准电压的极性直接计算作用时间，并通过控制零电平状态持续时间来控制中点电位。但以上方法无法消除中矢量对中点电位的影响，在高调制度和低功率因数情况下会产生低频振荡［11］。文献［12］提出了虚拟空间矢量脉宽调制（VSVPWM）策略，以流出中点电流为零为原则，重新定义中矢量，可以实现全调制度和全功率因数内的中点平衡。但该方法缺少中点电位反馈控制，因此在中点偏移情况下的平衡控制效果并不理想。文献［13］在VSVPWM 的基础上，利用冗余小矢量的分配对中点电位偏移进行控制，但在调制度较大的某些区域内，由于小矢量不参与合成，控制效果有限。文献［14］考虑到直流侧不平衡所引起的基本矢量变化，引入中点电位不平衡度进行补偿，中点控制效果较好。文献［15-16］重新定义虚拟矢量，通过选取含共模电压较小的基本矢量参与合成，可以在保持稳态中点平衡的基础上有效降低系统的共模电压，但由于参与合成的矢量非最近空间矢量，输出电压的谐波含量会有所增加。文献［17］采用断续脉宽调制（DPWM）策略，通过引入偏移信号，可以在保持系统较小开关损耗的同时实现中点平衡。文献［18-19］采用混合调制策略，在不同调制度下采用不同的调制方法，能有效抑制中点电压的波动，但计算过程较为复杂。文献［20-21］采用一种变虚拟空间矢量脉宽调制（VVSVPWM）方法，通过调整正、负小矢量作用时间来改变虚拟中矢量大小，进而改变中点电流，控制中点电位。该方法具有较高的稳态精度，但由于虚拟中矢量中仅有一对固定的小矢量进行调控，其在高调制度下的中点平衡能力有限。

本文为提高逆变器中点电位的动态平衡效果，在可变虚拟中矢量概念的基础上，提出了一种改进的变虚拟空间矢量脉宽调制（I-VVSVPWM）方法。该方法将虚拟中矢量中包含的基本小矢量拓展成两对冗余小矢量，并引入变虚拟中矢量平衡因子，在保持VVSVPWM 算法中变长系数取值的前提下，根据变虚拟中矢量平衡因子值计算补偿的电荷量并据此确立矢量顺序，从而在保持中点电位稳态精度的基础上，提高中点偏移时的动态平衡速度。此外，针对所提算法在动态平衡过程中输出状态反复切换的问题，本文进行了原理分析并引入相占空比法进行优化，在保持中点平衡能力不变的基础上，有效降低了系统的输出状态切换次数。最后，通过仿真和实验对所提调制算法的有效性进行验证。

1 NPC 三电平逆变器拓扑结构

I 型NPC 三电平逆变器拓扑结构如图1 所示，每相由4 个可控开关管和2 个钳位二极管构成。图1 中：ia、ib、ic为逆变器输出的三相电流；Udc为逆变器直流侧总电压；C1、C2为直流侧上下电容；Ls为滤波电感；Zload为负载。

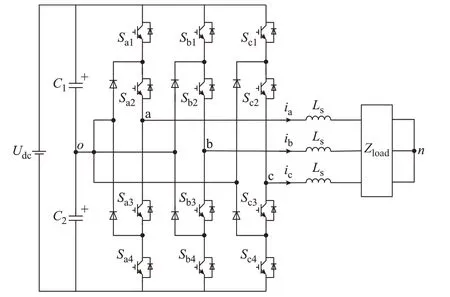
图1 I 型NPC 三电平逆变器拓扑结构Fig.1 Topology of I-type NPC three-level inverter

以a 相为例，令a 相的开关状态为Sa，对应的4 个功率开关管的状态记为Sa1、Sa2、Sa3和Sa4，则a 相输出状态及电压与器件导通的对应关系如表1所示。

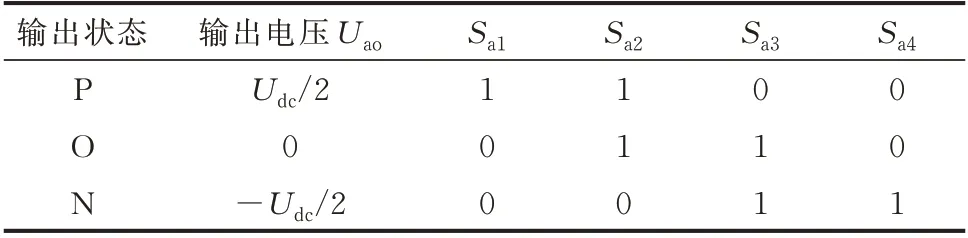
表1 a 相输出状态及电压与器件导通对应关系Table 1 Corresponding relationship between a-phase output state and voltage and device conduction

由表1 可知，三电平逆变器共有33=27 种输出状态，对应27 个基本空间电压矢量。NPC 三电平逆变器的基本空间电压矢量图如附录A 图A1 所示。

根据空间电压矢量的模值和其对中点电位的作用，可以将27 个空间电压矢量分为5 类：零矢量、正小矢量、负小矢量、中矢量和大矢量。其中，零矢量和大矢量对中点电位不产生影响。设电流从逆变器侧流向负载侧为正方向，则中小矢量作用时产生的中点电流如附录A 表A1 所示。

由附录A 表A1 可知，正负小矢量对应产生的中点电流大小相等，方向相反，可以相互抵消，而中矢量产生的电流则无法进行抵消，因此传统的SVPWM 算法在高调制度和低功率因数情况下，中点电压存在不能完全平衡的区域。而传统的VSVPWM 通过合成新的小矢量和中矢量，能够减小其对中点电压产生的影响。

2 传统的三电平逆变器VSVPWM 算法

2.1 VSVPWM 算法原理

VSVPWM 算法的基本思想是利用基本小矢量和中矢量合成虚拟中矢量，使得其在一个开关周期内产生的中点电流满足ia+ib+ic=0，此时逆变器可以在全调制度和全功率因数的范围内实现中点平衡。VSVPWM 算法在A 大扇区的矢量分布如附录A 图A2 所示，其他扇区的矢量分布图通过变换皆可归算到A 大扇区。VSVPWM 算法中各虚拟矢量的定义为：

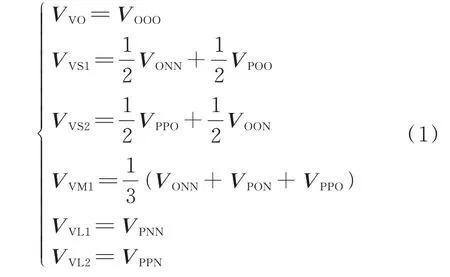
式中：VOOO为基本零矢量；VONN、VPOO、VPPO、VOON为基本小矢量；VPON为基本中矢量；VPNN、VPPN为基本大矢量；VVO为该算法下的虚拟零矢量；VVS1、VVS2为该算法下的虚拟小矢量；VVM1为虚拟中矢量；VVL1、VVL2为该算法下的虚拟大矢量。

在确立参考电压矢量Vref所处的小扇区后，根据最近三矢量原则选出参与合成的矢量，然后由伏秒平衡原理可以计算出三矢量的作用时间。在选择出合成Vref所需的三矢量并计算作用时间之后，即可确定电压矢量的作用顺序。

2.2 VVSVPWM 算法原理

传统的VSVPWM 算法在附录A 图A2 中的A5扇区内，并没有成对的冗余小矢量进行中点平衡，因此当中点电位发生偏移时，中点平衡的效果并不理想，为此文献［20］提出一种VVSVPWM 算法。

VVSVPWM 算法的基本思想是通过调整虚拟中矢量的长度，从而调整虚拟中矢量在一个开关周期内所产生的中点电流，使得虚拟中矢量也具有调整中点电位的能力，增强了高调制度下中点电位的平衡效果。VVSVPWM 算法在A 大扇区的空间矢量图如附录A 图A3 所示，各个虚拟矢量的定义为：

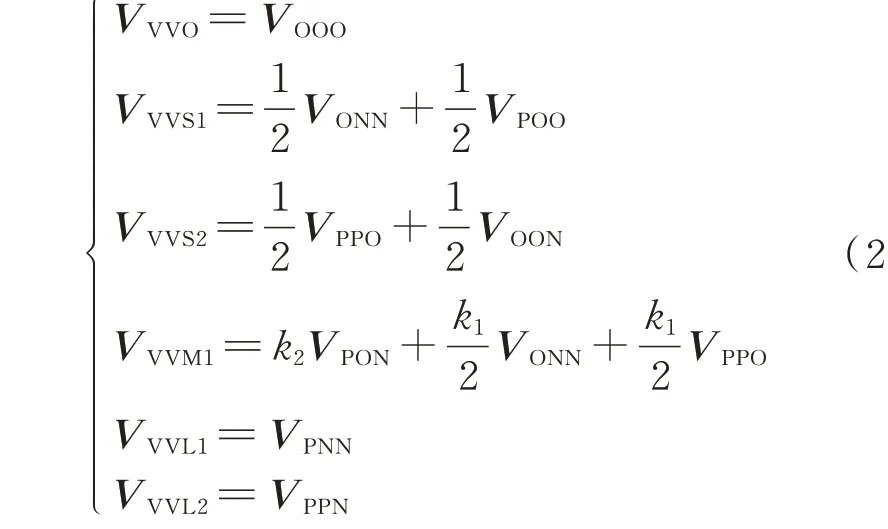
式中：VVVO为该算法下的虚拟零矢量；VVVS1、VVVS2为该算法下的虚拟小矢量；VVVM1为变虚拟中矢量；VVVL1、VVVL2为该算法下的虚拟大矢量；k1、k2为变长系数，满足k1+k2=1，0＜k1＜1、0＜k2＜1。

同样地，在确立参考电压矢量Vref所处的小扇区后，可以根据最近三矢量原则选出参与合成的虚拟矢量，然后由伏秒平衡原理计算出三矢量的作用时间，最后确定电压矢量的作用顺序，如附录A 表A2 所示。

VVSVPWM 方法的虚拟中矢量中包含了可控的基本小矢量，因此能实现A5 区域的中点电位控制，但由于该虚拟中矢量中仅有固定的一对冗余小矢量参与调节，其中点平衡能力有限。

3 改进的VVSVPWM 算法

为了进一步提高中点电位在高调制度下的平衡能力，本文对VVSVPWM 算法中的虚拟中矢量进行了重新定义，提出一种I-VVSVPWM 算法。该算法在虚拟中矢量的定义中包含两对冗余小矢量，其基本思想是对虚拟中矢量中的两对冗余小矢量进行选择并确定其相应的矢量序列，从而在保持中点平衡稳态精度的前提下，提高中点电位的动态平衡速度。

3.1 变虚拟中矢量定义与电荷量分析

重新定义的变虚拟中矢量为：

式中：k为变虚拟中矢量平衡因子，满足0≤k≤1。

设电流从逆变器侧流向负载侧为正方向，则由式（3）的定义可知，变虚拟中矢量在其作用时间TM内流出中点的电荷量QM为：

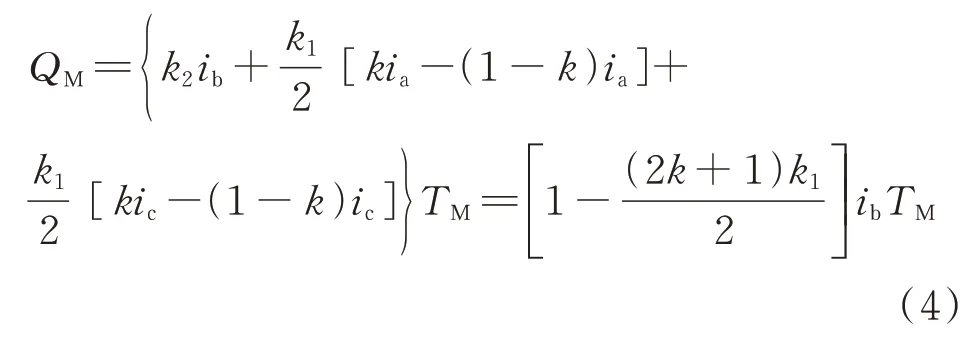
由式（4）可知，k、k1、ib均会影响流出中点的电荷量。当k1=2/3、k=1 时，变虚拟中矢量同传统VSVPWM 的虚拟中矢量相一致，不具备中点平衡的能力。为使变虚拟中矢量在电荷量可控的同时仍具有一定的中点平衡能力，同时为分析本文算法与VVSVPWM 算法［20］在k1取值相同时，由不同的k值引起的补偿电荷量的差异，以进行中点平衡能力的定量对比，本文选取k1的值为其临界值与2/3 的中间点，即k1=1/3 或k1=5/6。令变虚拟中矢量的作用时间为TM，对其流出中点的电荷量QM进行分析。

1）当k1=2/3、k=1 时，QM=0，此时该变虚拟中矢量与传统VSVPWM 的虚拟中矢量定义相同，不具备恢复中点平衡的能力，逆变器具有较低的中点电位波动。

2）当k1=1/3 时，此时中矢量流出中点的电荷量为：

（1）当ib＞0 时，中矢量作用时间内流出中点的电荷量的最大值和最小值分别为：

由上述分析可知，当QM≠0 时，变虚拟中矢量具有中点电位调节的能力，且调节能力随k和k1的取值变化而变化，为后面电压矢量序列的选择提供了参考。

3.2 小扇区划分

对于新定义的虚拟中矢量，在k1取值确定的情况下，k的取值并不会影响其模长，因此小扇区的划分方法同VVSVPWM 一致（见附录A 图A3），将其重新整理至图2。

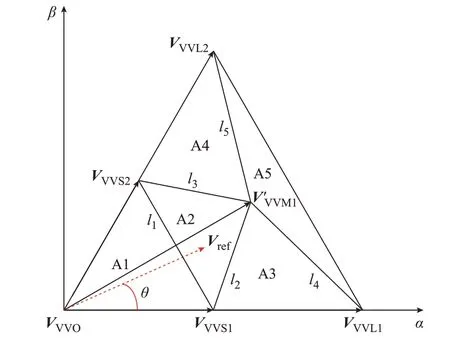
图2 I-VVSVPWM 算法在A 大扇区的矢量图Fig.2 Vector diagram of I-VVSVPWM algorithm in large sector A

式 中：Vα、Vβ和Vg、Vh分别为参考电压矢量Vref在α-β和g-h坐标系下的投影长度。

然后，计算图2 中划分小扇区的直线方程：

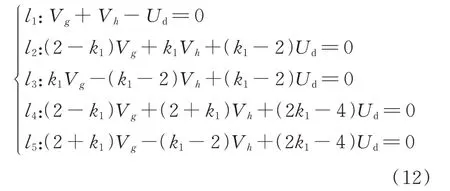
可以看到，式（12）中不含三角函数和根式计算，运算量有效降低。令直线方程等式左边的表达式分别为m1～m5，则小扇区的判断规则如附录A 表A3 所示。

3.3 三矢量作用时间计算

在确立参考电压矢量Vref所处的小扇区后，需要根据最近三矢量原则选取合成Vref所需的三矢量并计算其作用时间。为简化计算，仍在g-h坐标系下进行运算，以A2 小区域为例，根据伏秒平衡原理可以列出参考电压矢量的合成方程为：

式中：Ts为开关周期；Ta、Tb、Tc为三矢量各自的作用时间；Um=Ud（1-k1/2）为虚拟中矢量V′VVM1在g-h坐标系下的投影长度。

由式（13）可以解得：

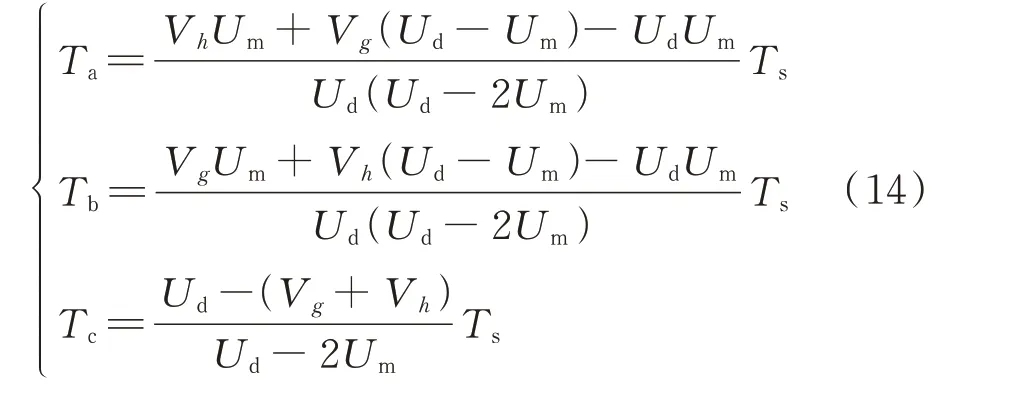
同理，可得到A 大扇区中其他区域的矢量作用时间如表2 所示。

表2 A 大扇区虚拟矢量作用时间Table 2 Action time of virtual vectors in large sector A

3.4 中矢量因子选择

由于系数k和k1会影响到基本合成矢量的选择，在此对其取值进行分析。从3.1 节中对虚拟中矢量所产生电荷量的分析可知，在k1取值确立的基础上，虚拟中矢量产生的流出中点电荷量的最大值或最小值只存在于k=0 或k=1 处。设H为允许的上下电容电压偏差，ΔU为实际的上下电容电压差，UC1、UC2分别为上下电容电压，则ΔU=UC1-UC2。

1）当-H≤ΔU≤H时，电容电压偏差在允许范围之内，无须中点平衡控制。此时，直流侧只需保持较低的中点电位波动，虚拟中矢量无须具有平衡中点电压的能力，因此取k1=2/3、k=1。

2）当ΔU＜-H时，电容电压偏差值超过允许的下限值，此时需要进行中点平衡控制，降低下电容电压。为维持中点平衡，需要满足流出中点的电荷量QM＞0：

（1）当ib＞0 时，有3 种情况：

由式（15）及变虚拟中矢量的定义可以看出，当k1=1/3，k=1 时，对应的补偿电荷量为VVSVPWM算法所能补偿的电荷量，此时该电荷量并非目前情况所能补偿的最大电荷量。为使中点电位快速恢复平衡，|QM|应取最大值（5/6）|ib|TM，此时对应k1=1/3，k=0。

（2）当ib＜0 时，此时k和k1的取值只有 一种情况：k1=5/6，k=1。此时流出中点电荷量的绝对值为：

3）当ΔU＞H时，电容电压偏差值超过允许的上限值，此时需要进行中点平衡控制，提高下电容电压。为维持中点平衡，需要满足流出中点的电荷量QM＜0：

（1）当ib＞0 时，此时k和k1的取值只有一种情况：k1=5/6、k=1。此时流出中点电荷量的绝对值如式（16）所示。

（2）当ib＜0 时，有3 种情况，如式（15）所示。

同理，当k1=1/3、k=1 时，对应的补偿电荷量为VVSVPWM 算法所能补偿的电荷量，此时该电荷量并非目前情况所能补偿的最大电荷量。为使中点电位快速恢复平衡，|QM|应取最大值（5/6）|ib|TM，此时对应k1=1/3、k=0。

综上，k和k1的取值流程图见附录A 图A4。

3.5 确立矢量顺序

在确定好中矢量因子k和k1的取值之后，需要对矢量的作用顺序进行合理的分配。电压合成矢量的分配需遵循以下原则：1）每相输出状态仅在P→O 以及O→N 切换，不能出现P→N 直接切换的情况；2）每个开关周期首发小矢量均为正小矢量。根据以上原则，初步定义A 大扇区的基本矢量作用顺序如附录A 表A4 所示（取前半个开关周期）。

由附录A 表A4 可知，所提算法依据单位开关周期内所能补偿的电荷量确定k值及矢量顺序，但在k=0 时会出现两相输出状态同时切换的情况，而输出状态的切换直接反映着开关管的切换，故此时的矢量顺序并不合适。为此，本文采用相占空比法进行优化，在保持中点平衡能力的情况下，确立最终的矢量顺序。

对于三电平逆变器而言，从直流侧中点o流出的中点电流等于连接至中点o的各相电流之和，因此在一个开关周期内从中点流出的电荷量为：

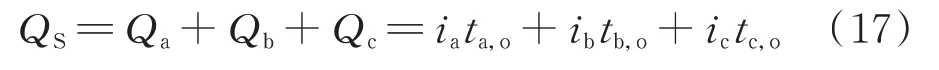
式 中：Qa、Qb、Qc分 别 为 三 相 所 能 产 生 的 中 点 电 荷量；ta，o、tb，o、tc，o分别为三相O 状态所持续的时间。

由式（17）可知，在不改变各相O 状态持续时间的前提下，更改某相输出电平的作用顺序并不会改变该相产生的流出中点的电荷量，即不会对中点电位平衡能力产生影响，此即为相占空比法的原理依据。现以A2（k=0）区域为例进行优化，附录A 图A5 给出了优化前A2（k=0）区域对应的输出状态图，未进行优化时，三相桥臂的输出状态在半个开关周期内分别切换了1、4、1 次，总共切换了6 次。引入相占空比法进行优化，在保证各相各电平作用时间占空比不变的情况下，将输出电平进行微调，将b 相P 状态移至最前，N 状态移至最后，得到优化后的矢量顺序如附录A 图A6 所示。

可以看到，优化后a、b、c 三相桥臂的输出状态分别为P→O、P→O→N、O→N，三相总共切换4 次，相比优化前的切换次数有所降低，且符合矢量顺序的基本要求。其他空间矢量区域的优化过程与A2（k=0）区域类似，表3 总结了A 大扇区采用相占空比法后最终确立的矢量顺序。

表3 相占空比法优化后的矢量顺序Table 3 Vector sequence optimized by phase duty cycle method

值得说明的是，在输出状态优化的过程中，由于各相各电平的作用时间占空比并未发生变化，各相输出电压在一个开关周期内的平均值也并未发生改变，合成的电压矢量也同优化前一致。实际上，相占空比法改变了矢量的作用顺序，但其中所包含的各相各电平的占空比信息是相同的，这些信息保证了相占空比法前后合成矢量和中点平衡能力的一致性。

3.6 中点平衡控制

当中点电位发生偏移时，此时需要利用平衡因子进行中点平衡。以A2 小区域为例，由于虚拟小矢量和变虚拟中矢量均可进行中点平衡控制，故单位开关周期内流出中点的总电荷量QS为：

其中，k和k1的取值在3.4 节中已经给出，故由式（20）即可得到r的取值。

综上，本文所提调制算法的整体实现流程如图3 所示，其中：N为大扇区位号，n为小扇区位号，ta，x、tb，x、tc，x分 别 为 三 相 各x状 态 所 持 续 的 时 间，x=p，o，n 分别表示P、O、N 状态。

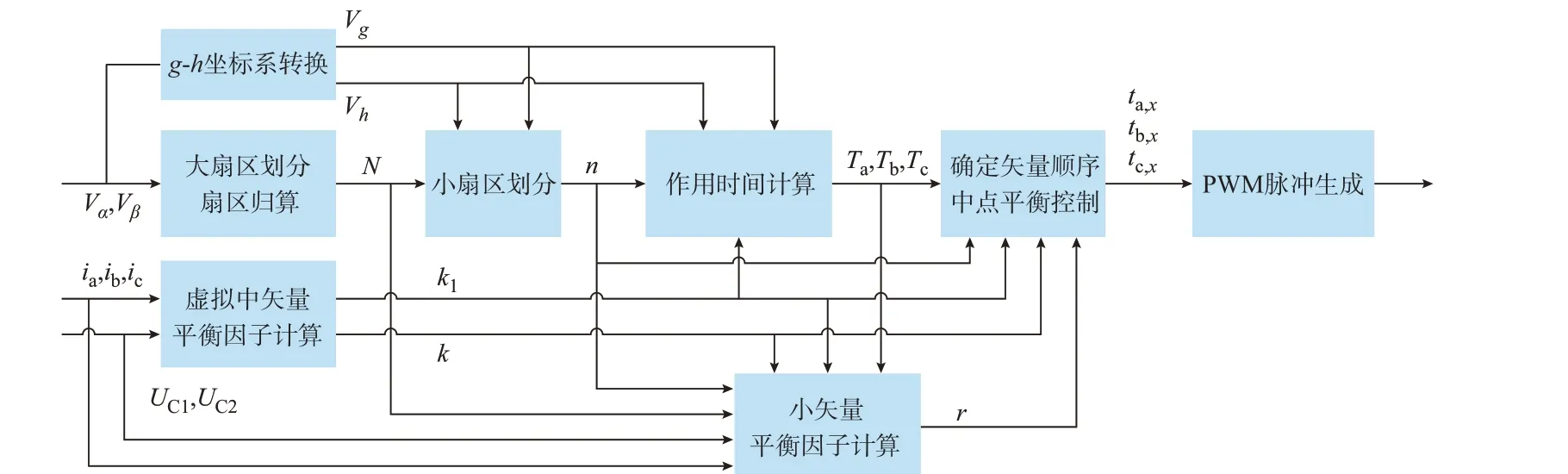
图3 I-VVSVPWM 算法实现流程图Fig.3 Flow chart for implementation of I-VVSVPWM algorithm

4 仿真分析和实验验证

4.1 仿真分析

为验证本文所提调制策略的有效性，在MATLAB/Simulink 中搭建了仿真模型进行验证。其中主电路采用I 型NPC 三电平逆变器拓扑结构，直流母线电压Udc=50 V，直流侧上下电容值C1=C2=4 000 μF，开关频率fs=12 kHz，输出频率f1=50 Hz，调制度m=0.8，功率因数cosφ分别为1（阻性）和0.3（阻感性）。

附录A 图A7 给出了高功率因数条件下的SVPWM、VSVPWM、VVSVPWM 以及输出状态优化后的I-VVSVPWM 这4 种调制算法的输出线电压、相电流以及上下电容电压波形，其中，上下电容电压初始偏差维持在20 V，在t=0.06 s 时进行中点平衡。由图A7 可知，SVPWM 的中点电压波动为0.1 V，其余3 种算法的中点电压波动为0.05 V，而 SVPWM、 VSVPWM、 VVSVPWM、 IVVSVPWM 这4 种调制算法的中点电位动态平衡时间分别为30、74、53、46 ms。由此可以看出，在高功率因数条件下，SVPWM 算法具有最快的动态恢复速度，但具有一定的中点电位波动，VSVPWM 算法具有较低的中点电位波动，但动态恢复速度较慢。VVSVPWM 算法和本文算法介于两者之间，且本文算法在保证稳态精度的前提下，动态恢复速度相比VVSVPWM 有所提高。

此 外，SVPWM、VSVPWM、VVSVPWM、IVVSVPWM 这4 种调制算法的线电压总谐波畸变率（THD）分 别 为38.43%、51.52%、51.47% 和51.52%，这是由SVPWM 与VSVPWM 算法中矢量合成规则的不同所引起的。VSVPWM 在一个开关周期的矢量顺序中含有P→O→N 的电平转换，电压变化率du/dt较大，故线电压THD 相比SVPWM 较大，这点在线电压波形中也可体现。而其余3 种调制策略在稳态时采用相同的矢量合成顺序，故输出线电压的THD 基本一致。

附录A 图A8 给出了低功率因数条件下4 种调制策略的输出线电压、相电流以及上下电容电压波形。由图A8 可知，SVPWM 算法的中点电压波动为0.8 V，其余3 种算法的中点电压波动为0.05 V，而SVPWM、VSVPWM、VVSVPWM、IVVSVPWM 这4 种调制算法的中点电位动态平衡时间分别为123、335、84、64 ms。可以看出，在低功率因数条件下，SVPWM 算法会产生低频振荡，且中点平衡所需时间较长。而本文算法在保持稳态精度的基础上，具有最快的动态恢复速度，且中点平衡的优化效果相比高功率因数条件时更加明显，体现了良好的稳态和动态性能。为对所提调制算法进行更全面的分析，将所提算法与文献［14-16］进行了对比，对比结果及相关分析见附录B。

为了验证所提算法的抗扰性能，附录A 图A9给出了该算法在负载和直流电压扰动下的上下电容电压变化过程。其中，调制度m=0.8，负载功率因数cosφ=0.3，初始上下电容电压为22.5 V。系统在t=0.1 s 时由空载转为带载，在t=0.2 s 时将直流电压由45 V 提升至55 V。由图可知，在负载和直流电压扰动情况下，本文调制算法均可以快速实现中点平衡，且中点电位波动很小，体现了该方法较强的抗扰性。

对于开关状态的优化，由于开关管的通断反映了开关状态的切换，本文通过开关管的导通次数来验证开关状态的切换次数。图4 给出了几种算法的三相开关管总导通次数对比以及相占空比法优化前后的平衡过程对比。

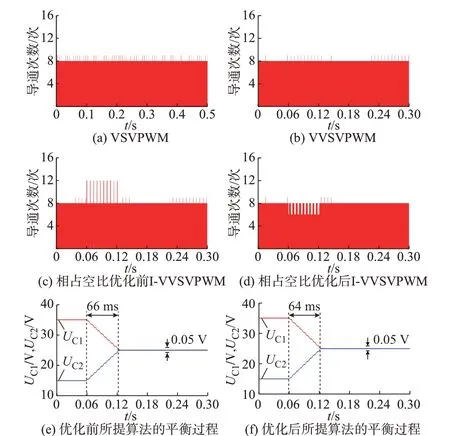
图4 各算法的三相开关管总导通次数对比以及所提算法在输出状态优化前后的电压平衡过程对比Fig.4 Comparison of total conduction times of threephase switch of each algorithm and voltage balancing process of the proposed algorithm before and after output state optimization

从图4（a）至（d）可知，输出状态优化前，所提算法在动态平衡时的开关管导通次数较多，这是由于开关状态在k=0 时的反复切换所导致；而在优化过后，所提算法在动态平衡时的导通次数明显减少，反映了采用相占空比法优化的有效性。根据图4（e）和（f）可知，本文算法在输出状态优化前后的中点平衡时间基本不变，体现了中点平衡能力的一致性。

从图4（a）至（d）中还可看出，各调制策略的开关管导通次数在某些时刻超过8 次，这是由于不同大扇区的首发作用矢量不同，参考电压在从某个大扇区向下一个大扇区转换的过程中，会产生额外的输出状态切换，使得开关管的总导通次数超过8 次。

4.2 实验验证

为验证本文所提调制算法的可行性，在实验室搭建了NPC 三电平逆变器的实验平台。该平台采用Freescale MC56F84789 DSP 和EPM570T100C5 N CPLD 作为控制器，采用F3L150R07W2E3_B11模块化绝缘栅双极型晶体管（IGBT）作为主开关器件。调制度m=0.8，C1=C2=4 000 μF，负载分别为阻性负载R=3 Ω 和阻感性负载R=1.5 Ω、L=15 mH，死区时间设置为2 μs，其余参数同仿真一致，实验平台照片如附录A 图A10 所示。

图5 和图6 分别为阻性和阻感性负载下采用4 种调制算法的上下电容电压的平衡过程图，初始电压偏差通过软件设置为20 V。

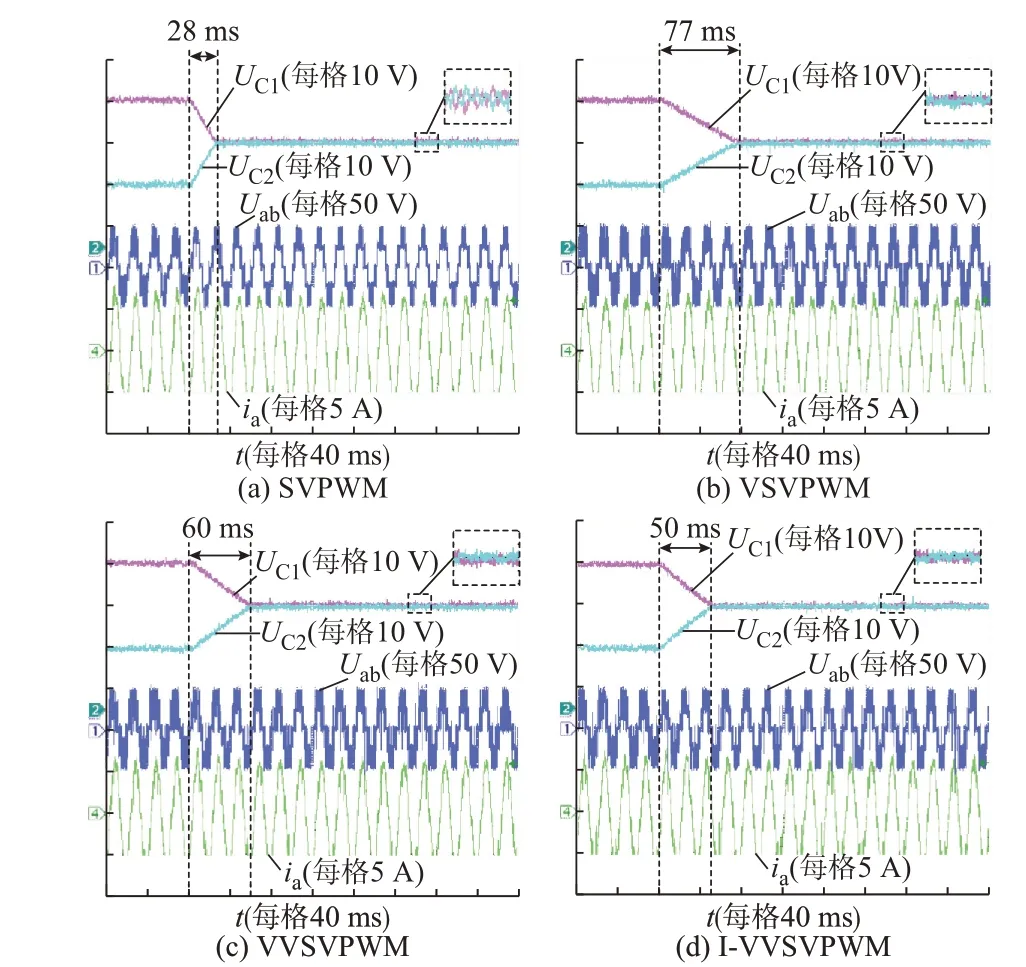
图5 阻性负载下4 种调制算法的电容电压平衡过程Fig.5 Capacitor voltage balancing process of four modulation algorithms with resistive load

由图5 和图6 可知：在阻性负载下，SVPWM 的中点平衡时间最短，但具有一定的中点电位波动，而其余3 种算法均可以保证中点电位稳态精度，同时本文算法具有最快的动态平衡速度；在阻感性负载下，SVPWM 的中点电位波动进一步加大，且平衡时间也有较大增加，而本文算法仍然可以保持良好的稳态精度和动态平衡速度，说明本文方法在低功率因数负载下能够很好地抑制中点电位低频振荡，与仿真结果分析一致。

图6 阻感性负载下4 种调制算法的电容电压平衡过程Fig.6 Capacitor voltage balancing process of four modulation algorithms with resistive and inductive load

为更全面地进行分析，表4 给出了低功率因数下含文献［14］在内的5 种算法在不同调制度时的平衡时间tNP和逆变器输出线电压THD。当m≤0.5时，合成三矢量中不包含中矢量，中间3 种虚拟空间矢量调制算法所需的平衡时间基本相同。当m＞0.5 时，中矢量参与矢量合成，由于VSVPWM 的虚拟中矢量不产生补偿电荷，因此平衡时间相比另外几种调制有明显增加。另一方面，随着调制度增大，5 种调制算法的线电压THD 逐渐减小，这是由于输出电压从低调制度下的三电平转为高调制度下的五电平，正弦化程度逐渐明显。此外，SVPWM 的电压THD 小于其余调制算法，这是由于SVPWM 采用七段式合成，开关频率处的谐波要小于九段式的VSVPWM。对于后4 种调制算法，受到实验参数、噪声等影响，输出电压THD 不完全相同。但随着调制度的增大，杂散干扰对输出的影响占比逐渐减小，几种算法的电压THD 也趋于一致。

表4 不同调制度下各算法中点平衡时间及线电压THDTable 4 Neutral point balance time and line voltage THD of each algorithm with different modulation degrees

根据表4，可以得到图7 所示的不同调制度下各算法的中点平衡时间。由图7 可知，与前3 种算法相比，当调制度m＞0.5 时，随着调制度增加本文所提算法的中点平衡速度优化效果愈发显著，体现了所提算法的优越性；与文献［14］相比，当0.5＜m＜0.8时，由于虚拟中矢量和小矢量共同参与中点控制，因此所提算法的中点平衡速度较快。而当调制度继续增加时，由于所提算法仅由中矢量参与中点控制，其中点平衡能力会逐渐弱于文献［14］。

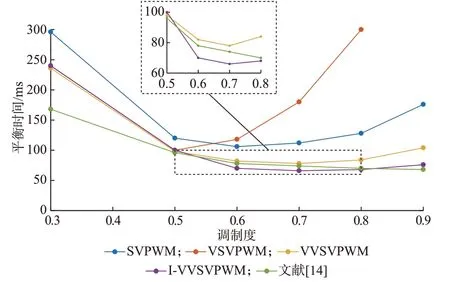
图7 不同调制度下各算法的中点平衡时间(cos φ=0.3)Fig.7 Neutral point balance time of each algorithm with different modulation degrees (cos φ=0.3)

附录A 图A11 给出了负载和直流电压扰动下的上下电容电压平衡过程图，其中负载由空载转为带载，直流电压由45 V 变化到55 V。可见，本文算法在负载突变和直流母线电压变化情况下，均可以快速稳定地实现上下电容电压的平衡，动态跟踪性能较好。

综上，本文所提算法的中点电位相比SVPWM有更高的稳态精度，相比于VSVPWM 与VVSVPWM 有更快的动态平衡速度，且在不同功率因数条件下均有较好的平衡效果，其综合性能更优。

5 结语

针对NPC 三电平逆变器的中点平衡问题，本文提出一种I-VVSVPWM 方法，该方法重新定义了虚拟中矢量，分析其在单位开关周期内所能产生的电荷量，并据此确立合适的矢量顺序，可以使系统在保持中点电位稳态精度的基础上提高其动态平衡速度。此外，本文引入g-h坐标系对计算过程进行简化，并对所提方法的开关状态进行了分析和优化。通过对仿真和实验结果的分析和讨论，可以得到以下结论：

1）所提算法在不同功率因数条件下均可以有效抑制中点电位波动，较快地实现中点平衡，且在高调制度、低功率因数的条件下对平衡速度的优化效果更加明显。

2）采用相占空比法可以在保持中点平衡能力和合成矢量不变的前提下，减小系统在动态平衡过程中的输出状态切换次数。

在本文的研究中，重点关注了系统的中点平衡问题，而对系统的共模电压抑制等方面没有涉及。因此后续将结合现有基础，深入探究能够兼顾中点平衡和共模电压抑制的控制方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。