基于分布式深度强化学习的微网群有功无功协调优化调度

巨云涛，陈 希，李嘉伟，王 杰

（1. 北方工业大学电气与控制工程学院，北京市 100144；2. 中国农业大学信息与电气工程学院，北京市 100083）

0 引言

微网（microgrid）是一种将分布式电源（distributed generator，DG）、负荷、储能装置及监控保护装置有机整合在一起的小型源网荷储系统［1-5］，是消纳分布式新能源和提高配电网可靠性的有效手段。然而，单个微网存在抗扰动能力差、工作容量有限且缺乏备用的缺点。针对以上问题，研究人员提出将相邻微网互联构成微网群（networked microgrids，NMG）［6-7］，并通过有效的优化调度策略协同调度，提升对新能源不确定性的适应性［8］。由于微网阻抗比较大，有功和无功功率间存在着强耦合关系，并且大量DG 的接入使得潮流由传统的单向流动变为双向流动，电压越限问题严重，仅调控有功资源并不能保证系统运行的安全和经济性，需要同时协调有功和无功资源［9-11］。

目前，有功无功协调优化调度问题的求解方法主要有基于物理模型的优化方法和数据驱动的方法两类。基于物理模型的优化方法中，文献［12］对配电网有功无功协调优化调度问题建立二阶锥规划模型并求解。文献［13-14］在文献［12］的基础上，应用场景法处理可再生能源和负荷的不确定性。文献［15］则利用区间描述不确定性，建立基于区间不确定性的微网有功无功协调优化调度模型。而文献［16］则采用基于模型预测控制的方法处理含不确定性的优化调度问题。但上述方法均为集中式方法，无法保障各子微网信息的隐私性且通信压力较大［17］。虽然已有文献通过引入交替方向乘子法（alternating direction method of multipliers，ADMM）实现了微网群的分布式优化调度［18-19］，但ADMM 对通信系统的要求较高。同时，无论是集中式优化还是分布式优化，均无法避免对精确电网模型的依赖。

基于数据驱动的方法中，深度强化学习（deep reinforcement learning，DRL）被证明是解决无模型优化决策问题的有效方法，已在电力系统能量管理［20-21］、无功优化［22-23］、需求响应［24］、紧急控制［25］等方面开展了大量研究。文献［26］提出了基于DRL的有功无功协调优化方法，但文中并未考虑离散变量。文献［27］设计了一种基于混合随机变量联合分布的随机策略，适应了离散-连续混合动作空间。然而，上述DRL 算法只能训练单一智能体，与集中式优化面临着相同的问题。对此，多智能体深度强化 学 习（multi-agent deep reinforcement learning，MADRL）给出了解决方案［28］。文献［29-30］将DRL扩展为MADRL，通过训练多个智能体实现分布式控制。但是，文中采用“集中训练，分散执行”框架，集中训练期间未能保护各分区信息的隐私性。虽然文献［31-32］提出了基于通信神经网络的MADRL来克服集中训练的问题，但所提方法仅面向连续动作。此外，上述文献中均未考虑网络拓扑变化带来的影响。

综上所述，当前基于模型的传统集中式和分布式优化方法依赖于精确的网络模型且对通信要求高，而基于MADRL 的方法又难以同时适应分布式训练和离散-连续混合动作空间，并且缺乏对拓扑变化的处理。因此，为了解决上述问题，本文提出一种基于分布式MADRL 的微网群有功无功协调优化调度方法，具有以下优点。

1）在训练学习阶段，各智能体仅需本地观察量和其余智能体传递的少量信息，而无须像基于“集中训练”框架的MADRL 一样收集全局信息，减少了通信压力，保证了各子微网信息的隐私性。

2）采用的算法可以训练具有离散-连续混合动作空间的智能体，智能体在线执行阶段能够以毫秒级实时性给出近似集中式优化水平的调度策略。

3）考虑到一组智能体难以匹配多种网络拓扑下的调度任务，提出一种迁移强化学习方法，通过改进Critic 和Actor 网络函数，实现利用已有策略引导新智能体加速训练。

4）本文方法对通信要求低，且对通信故障具有较好的鲁棒性。在训练阶段，智能体间有限时间的通信中断并不会影响训练效果，而在执行阶段智能体间则无须通信。

本文的结构如下：首先，以网损最低为目标，构建微网群有功无功协调优化调度模型；然后，将该模型描述为马尔可夫博弈（Markov game）问题，给出各智能体的具体观察空间、动作空间以及奖励函数；进而，介绍用于训练多智能体组的分布式多智能体软演员-评论家（distributed multi-agent soft actorcritic，DMASAC）算法，以及迁移强化学习方法；最后，通过数值算例验证本文所提方法相较于其他算法的有效性和优越性。

1 微网群有功无功协调优化调度模型

1.1 目标函数

本文考虑通过合理控制光伏逆变器、静止无功补偿器（static var compensator，SVC）、分布式储能系统（distributed energy storage system，DESS）、有载调压变压器（on-load tap-changer，OLTC）、投切电容器组（capacitor bank，CB）等设备，使得调度周期内的网损最小。构造目标函数如下［12］：

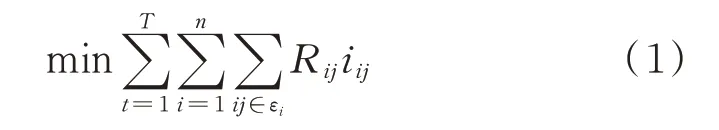
式中：n为子微网的个数；T为一天的总调度时段数；Rij为 支 路ij的 线 路 电 阻；iij为 支 路ij电 流 的 平 方；εi为子微网i的支路集合。

1.2 约束条件

1）潮流约束为：

2）光伏出力约束。为提高经济性，规定光伏系统以最大功率发电，仅无功功率可调［33］，即

4）支路传输功率约束。支路上传输的有功功率约束为：

式 中：Pij，t为 支 路ij在t时 刻 传 输 的 有 功 功 率；Pˉij为支路ij传输的有功功率最大限值；ε为支路集合。

5）电压幅值约束。各个节点的电压幅值约束为：

2 基于分布式MADRL 的微网群有功无功协调优化调度

2.1 微网群分布式优化调度的马尔可夫博弈模型

MADRL 方法是令智能体与环境进行多轮交互，通过“试错”学习到最优策略。每轮交互均从环境初始状态开始，各智能体会先观察局部环境状态，再根据自身策略由观察量选择动作，并使环境进入下一状态，然后获得环境给予的奖励，从而对自身策略进行优化。重复上述过程，直到环境状态达到终止状态便完成一轮训练。通过在交互过程中对自身策略的逐步优化，智能体获得的累积奖励会逐渐增加直至趋于稳定。

上述交互过程常用马尔可夫博弈定量描述，其包括6 个要素，采用元组S，Oi，Ai，P，R，γ表示。其中，S代表公共环境的所有状态集，t时刻的状态为st∈S；Oi为智能体i的局部观察集，t时刻智能体i的本地观察为oi，t∈Oi，n个智能体的观察联合在一起组成了联合观察O=O1O2…On；Ai为智能体i的动作集，t时刻智能体i的本地动作为ai，t∈Ai，n个智能体的动作联合组成了联合动作A=A1A2…An；P为状态转移概率，表示在状态st下执行联合动作at后使环境进入下一状态st+1的概率；R为奖励函数，表示在状态st下智能体组执行联合动作at后，环境给 予 的 反 馈 奖 励，满 足stat→rt，rt∈R；γ为 折 扣因子。

利用MADRL 求解具体问题的关键在于对上述马尔可夫博弈进行设计。在微网群有功无功协调优化调度背景下，给出各智能体的观察、动作空间以及奖励函数的具体设置，如下所述。

1）智能体观察空间

智能体的观察空间是智能体对本地环境的感知信息。这里，设定智能体i的局部观察量为每个时间步t本地各节点负荷功率、可再生能源发电功率、储能的电量、OLTC 和CB 的挡位以及时刻t。同时，为了考虑离散设备的动作次数约束，将OLTC和CB 已动作的次数也加入观察空间，如式（17）所示。

2）智能体动作空间

智能体的动作空间是本地可控设备的调节量。由于本地既有离散调节设备又有连续调节设备，故这里智能体的动作空间包括离散动作空间和连续动作空间，即

3）智能体奖励函数

需要注意的是，由于不存在协调中心，策略优化时无法直接获取系统的总网损以及总越限惩罚。观察式（21）可以分解为各子微网的本地网损和越限惩罚再累加，因此，可以通过智能体间的通信传递得到。由于并不涉及各子微网本地源荷出力、设备调度动作、网络参数以及运行成本等隐私信息，故并未侵犯隐私。

离散设备的动作次数有限，在动作次数越限之后强行加入一个惩罚容易导致训练结果发散。考虑到离散智能体的动作集有限，这里采用Mask 掩码约束离散智能体的动作，具体方法见附录A。

2.2 DMASAC 算法

本节介绍用于求解所提马尔可夫博弈模型的MADRL 算法。已知文献［34］采用经典的“集中训练，分散执行”框架，将软演员-评论家（soft actorcritic，SAC）算法扩展为多智能体软演员-评论家（multi-agent soft actor-critic，MASAC）算法，但在训练过程中各子微网的信息隐私性得不到保障。本文以MASAC 算法为基础，进行相应调整使其可以适应分布式训练以及离散-连续混合动作空间。

MASAC 算法仅适用于连续动作空间，为使其可以适应离散-连续混合的动作空间，需要对其进行改进。参考文献［35］对SAC 的更改，这里在每个智能体的Critic 网络中补充一个输出层，维数为hdim×Nˉ，其中hdim为隐藏层神经元的个数，Nˉ为本地离散设备的最大动作挡位，用于输出每个离散挡位对应的Q值。相应地，Actor 网络也补充一个输出层，维数同样为hdim×Nˉ，输出经Softmax 函数后，得到每个离散挡位对应的概率。修改后的Critic、Actor、Estimate 网络结构分别如附录B 图B2、图B3、图B4所示。

通过上述改进便得到了DMASAC 算法。算法的训练目标为寻找到智能体i的最优策略π*i，如式（26）所示。

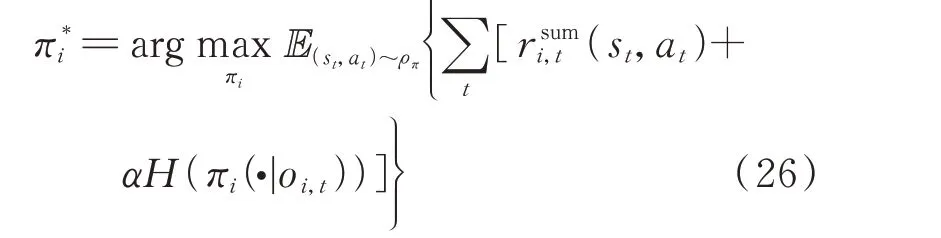
式中：E{·}表示求期望函数；(st，at)～ρπ表示由策略π诱导的状态动作轨迹分布；H(πi(·|oi，t))为智能体i在 观 察 量oi，t下 按 照 策 略πi采 取 动 作 的 熵；α为 温 度系数，用于调整动作熵相对于奖励的重要性。

上述寻优过程在智能体与环境交互的过程中进行，可简单描述为策略迭代更新。从一个随机策略π0开始，Actor 网络通过策略选择动作，而Critic 网络评估Actor 所选择动作的价值，并指导Actor 按照评估值最大更新策略参数，得到新策略π1，然后重复前述步骤，使得策略逐步提升。上述过程主要有两个关键步骤：策略评估（policy evaluation）和策略改进（policy improvement），分别对应Critic 和Actor网络的更新，具体流程见附录B。

2.3 拓扑变化后的迁移学习方法

多拓扑下的调度控制需要为每种网络拓扑训练一组对应的智能体。为提高训练效率，可以在上述DMASAC 的基础上引入迁移学习机制。

首先，将已训练好的智能体的Critic 网络参数迁移至新智能体，并将新智能体的动作价值函数修改为如式（27）所示的形式，以保证新智能体的Critic网络在初期能较为准确地评估动作的好坏。然后，借鉴文献［36］的思路，令已训练好的智能体的Actor网络作为教师模型，并在新智能体的Actor 网络的损失函数中补充一项与教师模型的“差距”，如式（28）所示。期望通过缩小“差距”，实现利用教师模型指导新智能体训练。不同于文献［33］，这里将“差距”描述为在同一状态下分别按教师策略和新智能体当前策略采样动作，进而得到的两动作价值之差，不仅更好地体现了利用教师模型引导新智能体向更高的动作价值方向学习，并且连续、离散动作空间均适用，很容易推广到其他基于Actor-Critic框架的算法。

3 数值算例

3.1 系统设置

为验证基于DMASAC 的微网群分布式有功无功协调优化调度方法的有效性，以改进IEEE 33 节点系统为例进行仿真研究。系统拓扑如附录C 图C1 所示，共分为3 个子微网，其中，在节点6、14、18、22、25、33 处接有光伏，装机容量为800 kW，逆变器视在功率为装机容量的1.05 倍；节点18 处接有储能装置DESS18，荷电状态（SOC）范围为0.1～0.9，充放电效率均为0.9，容量为2 MW·h；节点23、29 处接有SVC，无功调节范围为-500～500 kvar；节点8、27 处接有CB，共4 组，每组0.2 Mvar，一天内挡位最大调节次数为6；节点0、1 之间接有OLTC，一天内挡位最大调节次数也为6。调度周期为一天24 h，以1 h 为一个调度时段。

Critic、Actor、Estimate 网络均含有2 个隐含层，各层的神经元数量均为256。所有隐含层均采用ReLU 激 活 函 数。Critic、Actor、Estimate 网 络 的 学习率σ=0.001。折扣因子γ=0.99，温度系数α=0.1，延迟参数η=0.001。文中所有MADRL 算法均由Python 实现，利用了深度学习框架PyTorch。

3.2 训练效果分析

3.2.1 收敛性分析

为验证本文方法的收敛性，将负荷和光伏出力的历史数据作为训练样本，分别采用本文的DMASAC 算法和“集中学习，分散执行”框架的MASAC 算法训练智能体组，统计每个调度周期智能体组获得的累积奖励，生成奖励曲线如图1（a）所示，可以观察到两者在大概100 次训练后均收敛。如图1（b）所示，在约70 次训练后，智能体受到的约束越限惩罚趋于0，说明智能体动作被限制在合理的区间内。但是，在收敛性相当的情况下，采用DMASAC 训练并不需要收集全局信息，保障了各子微网信息的隐私性。

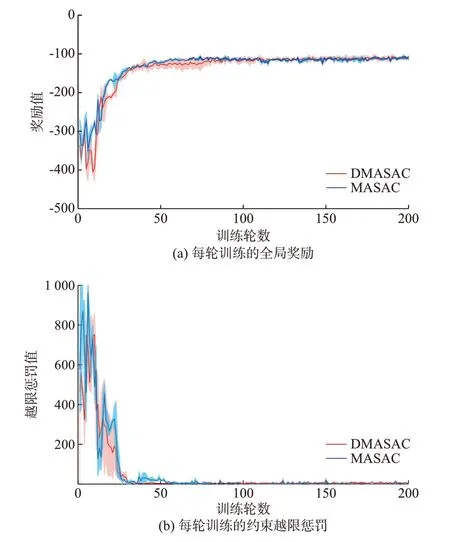
图1 DMASAC 与集中学习的训练结果对比Fig.1 Comparison of training results between DMASAC and centralized learning

为验证本文方法在处理离散-连续混合动作空间上的有效性，采用文献［37］中的双层强化学习算法作为对比算法，并比较其训练效果。如图2 所示，可以看到本文方法的训练效果更好，不仅智能体获得的累积奖励更大，而且智能体的约束越限惩罚也更小。这是由于双层强化学习算法中，连续智能体以离散智能体的调度动作为部分观察，而离散智能体获得的奖励大小又取决于连续智能体的动作优劣，导致两智能体的训练效果彼此相互影响。这种相互影响的存在，使得对于两智能体而言，环境都是不稳定的，训练更加困难。

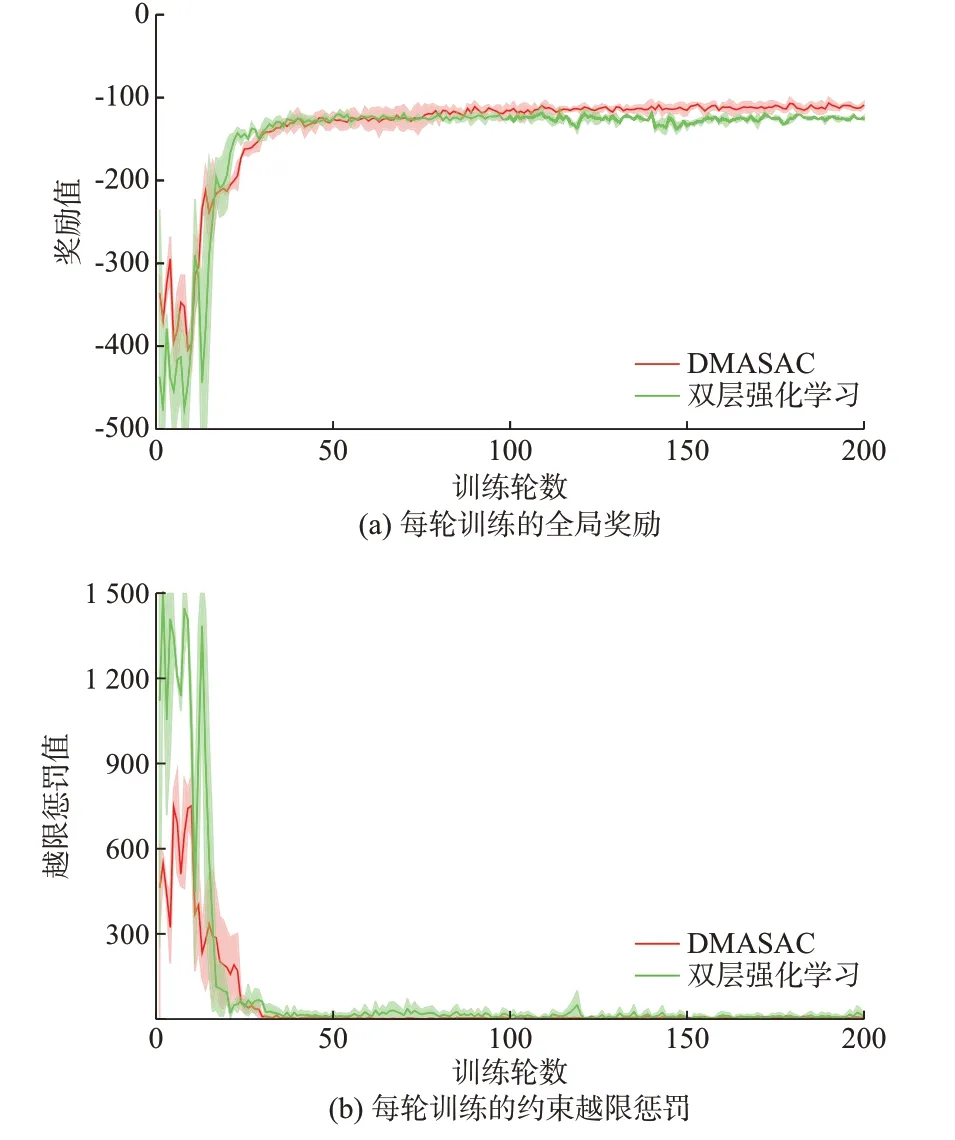
图2 DMASAC 与双层强化学习算法的训练结果对比Fig.2 Comparison of training results between DMASAC and bi-level reinforcement learning algorithms

3.2.2 训练所需通信数据量分析

对于MADRL，为克服多个智能体的存在导致的非马尔可夫性，在训练过程中智能体均需要来自其他智能体的信息。不同MADRL 算法所需的通信信息不同。

在改进的IEEE 33 节点3 微网算例下，训练过程中各算法需要的通信数据如表1 所示。可以看出在每个更新步，采用DMASAC 算法时智能体间传递的数据量明显少于采用集中训练框架的MASAC算法。在MASAC 中，每个智能体的Critic 和Actor网络在中央协调器中集中训练。要完成一个更新步，需要中央协调器向每个智能体i广播nstatei×nbatchi维从经验池采集的状态数据，其中nstatei为观察向量维数，nbatchi为采样个数。然后，从每个智能体获得nactioni×nbatchi维动作数据，其中nactioni为动作向量维数。对于集中式的双层强化学习算法，每个智能体的观察向量和动作向量均是全局信息，但采用DMASAC 算法时，各智能体拥有自己独立的经验池，仅需智能体间传递边界信息和奖惩信息，不仅通信数据量少，更保障了智能体的数据隐私性。

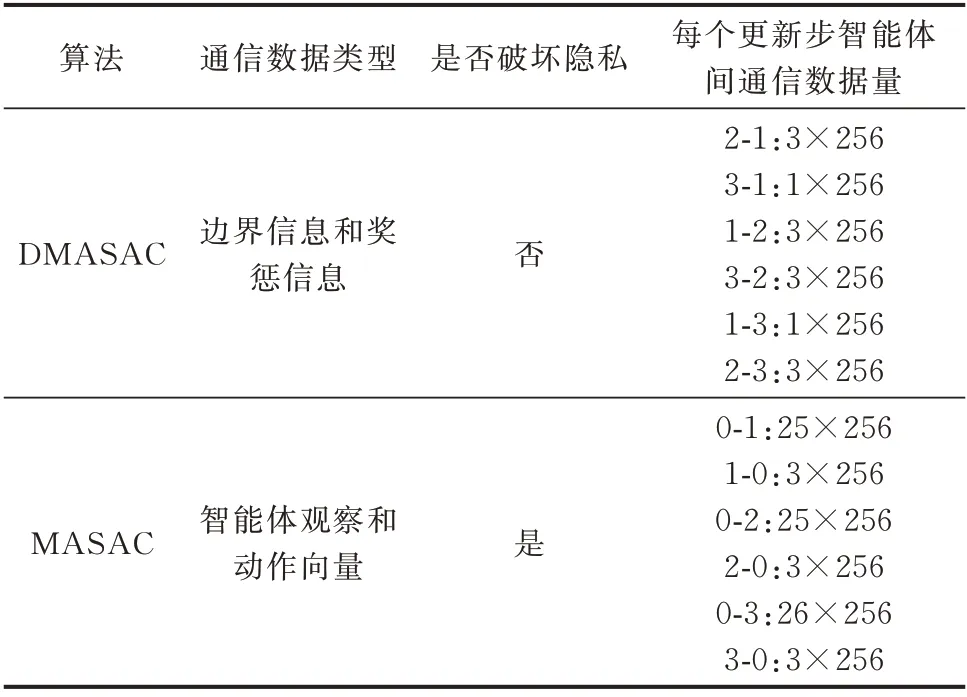
表1 各算法下的通信需求Table 1 Communication demand of each algorithm

3.2.3 训练对通信故障的鲁棒性分析

由于本文方法在训练阶段智能体间需要相互通信，考虑到通信系统非理想，难免出现通信中断、数据丢包等问题，这里对比不同程度的通信中断情况下智能体组的训练效果，如图3 所示。可以看出，有限时间的通信中断并不会对方法的收敛性造成很大的影响，这是因为在通信中断后，受影响的智能体不更新参数，保留当前策略，而当通信恢复后，智能体会继续训练，只要训练次数充足便能够收敛到与没有通信中断相当的结果。数据丢包同理，通信中断仅停止策略的更新优化，并不影响当前策略的执行。综上所述，本文方法对通信中断以及数据丢包等问题具有较好的鲁棒性。

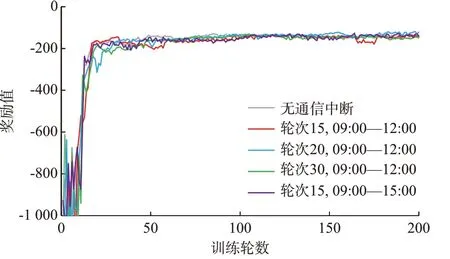
图3 不同通信中断情况下的训练效果Fig.3 Training effect under different communication interruption conditions

3.3 调度结果分析

选取某一天的源荷数据进行测试，见附录C 图C2，利用训练好的智能体组进行调度，调度结果如图4 所示。

图4 各设备调度结果Fig.4 Dispatching results of each equipment

由图4（a）可以看出，从09：00 开始，随着光伏出力的增加，储能充电达到容量上限，以就地消纳光伏、减少功率倒送；而在16：00 后，光伏出力不足以供应本地负荷，储能开始放电，直到21：00 达到容量下限并保持，以维持一个调度周期内储能的状态不变。通过上述调度方式，一定程度上实现了削峰填谷，减少了光伏波动性对系统带来的干扰。对于无功补偿装置，光伏逆变器的出力如图4（b）所示。可见，大部分光伏逆变器发出无功功率，以支撑电压并减小网损，仅节点6 和14 所接光伏逆变器在光伏出力较高时吸收无功功率，防止电压越限。

此外，节点29 和23 所接SVC 也根据所在节点的电压幅值，发出和吸收感性无功功率，进而平抑电压波动，如图4（c）所示。

离散设备在调度周期内的动作次数不宜过多，从图4（d）可以看出，OLTC 和CB 的动作次数均未超过限值。在01：00—08：00 以及18：00—24：00，光伏出力为0，OLTC 将挡位调至最高以提高系统电压等级，降低网损；在09：00—17：00 挡位下调，防止因光伏功率倒送引起电压越限。而节点27 和8 所接CB 则调整挡位用于提升节点27 和8 的电压。

为了直观地体现出本文方法的优化效果，比较了优化调度前后系统各时刻的网损以及电压幅值，分别如图5、图6 所示。从图中可以看出，采用有功无功协调调度显著降低了网损，并且改善了电压分布，治理了电压越限问题。

图5 各时刻网损Fig.5 Network loss at each moment

图6 优化前后各节点电压幅值Fig.6 Voltage amplitude of each node before and after optimization

为进一步验证本文方法的优越性，选用混合整数动态优化［38］和ADMM 作为传统优化方法的代表，选取3.2 节中的MASAC 和双层强化学习算法作为数据驱动方法的代表，与本文方法进行对比分析。为了较为全面地评估各方法的优劣，这里从多个方面对5 种方法进行对比，如表2 所示。

表2 不同方法的性能对比Table 2 Performance comparison among different methods

虽然传统优化方法在降低网损方面似乎更优，但这是因为传统方法的调度结果是在假设日前负荷、可再生能源出力预测数据以及网络模型参数均无误差的情况下求得的，而实际应用时无法达到上述理想条件。采用本文方法经过19 min 的训练，智能体能以毫秒级实现在线决策，且无须重复计算。同时，由于智能体基于历史源荷数据进行训练，其能够自适应学习到源荷的分布，从而适应源荷的不确定性。此外，相较于传统集中式优化方法，本文方法保护了各子微网信息的隐私性，相较于ADMM，本文方法则展现出对通信故障的鲁棒性：训练阶段的通信中断或数据丢包不会影响训练效果，执行阶段智能体间则无须通信，而相较于另外两种数据驱动方法，本文方法不仅在降低网损的效果上更优，并且能够保护隐私。综上所述，本文方法在整体处理效果上具有优越性。

3.4 迁移强化学习的训练效果分析

为验证迁移强化学习方法的有效性，仍以改进的IEEE 33 节点系统为例来比较迁移学习和普通训练的训练效果。IEEE 33 节点系统共分为3 个子微网（拓扑1），如附录C 图C1 所示，拓扑2、3 是分别在拓扑1 的基础上断开支路9-10 并连通支路9-15、断开支路7-8 并连通12-22 得到的，同时假设已在拓扑1 下训练好一组智能体，记为源智能体组。如图7 所示，在拓扑2、3 情况下采用迁移强化学习方式，均更快地实现了收敛。这是因为在引入源智能体作为教师模型修改新智能体网络损失函数后，在训练初期新智能体会向着源智能体的方向学习，相当于在源智能体的指导下探索环境，增强了前期探索的方向性，提高了学习效率。

图7 迁移强化学习训练效果Fig.7 Training effect of transfer reinforcement learning

4 结语

本文针对微网群的分布式有功无功协调优化调度问题，提出了一种基于MADRL 的方法。首先，相较于传统优化方法，所提方法得益于数据驱动的特性，训练时无需精确的微网群模型和源荷预测数据，训练后智能体仅依据本地观察量便能以毫秒级实时性给出调度动作，而且方法对通信故障具有鲁棒性；其次，与基于“集中训练”框架的MADRL 方法相比，所提方法在无全局信息的情况下也可达到与之等同的训练效果，在学习过程中保障了各子微网信息的隐私性。此外，还补充了一种迁移强化学习方法，用于系统拓扑变换后加速训练新智能体组，弥补了MADRL 模型泛化能力差的缺点。

然而，本文方法对于约束的处理仅是将其作为一种惩罚加入奖励函数中，虽然通过多轮训练使得惩罚降为零，但也影响了训练效率。因此，对约束的处理进行改进，令智能体在允许的范围内高效探索环境是值得进一步研究的方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。