计及用户热舒适度的综合能源系统可靠性指标及评估方法

2023-02-02王舒萍张沈习程浩忠

电力系统自动化 2023年1期

王舒萍，张沈习，程浩忠，原凯，宋毅，韩丰

（1. 电力传输与功率变换控制教育部重点实验室（上海交通大学），上海市 200240；2. 国网经济技术研究院有限公司，北京市 102209）

0 引言

“碳达峰·碳中和”等战略目标的提出为中国的能源转型和发展指明了新的方向，如何优化能源结构、促进能源高效合理利用已成为研究热点［1-2］。综合能源系统（integrated energy system，IES）实现了电、气、热（冷）等异质能源的关联耦合和互补互济，是未来能源系统的重要发展趋势［3-5］。然而，IES 中能源转换设备的多样化、不同能源系统运行特性的差异化以及能源耦合程度的逐步加深给系统的高可靠供能带来了挑战。实现IES 可靠性水平的定量评估是提高IES 供能可靠性水平的关键之一。

目前，国内外在IES 可靠性评估方面已有一定的研究成果。首先，在IES 可靠性指标方面：文献［6-8］选择能量不足持续时间、能量不足期望、供能可靠率、切负荷概率等常见指标来衡量IES 可靠性水平，然而，考虑到IES 中不同能源动态特性差异较大，不同能源子系统受到扰动后达到稳态过程的时间尺度各异，且IES 中存在复杂的耦合互联及供需不确定性因素，使得上述传统指标并不完全适用于IES 可靠性评估；文献［9］结合不同能源价格，定义了可靠性影响评价指标，该指标从价格方面评估设备故障对综合能源微网带来的影响；文献［10］通过引入设备的“阀级”概念，定义了设备重要程度指标来衡量不同设备对IES 可靠性水平的影响程度；文献［11］定义了可靠性提升率指标来反映储能和需求响应对IES 可靠性的影响；文献［12］计及热网延时特性和负荷热惯性对IES 供热可靠性指标进行了修正；文献［13］在考虑热网传热延迟的基础上，提出了适用于IES 中热力子系统的可靠性指标。其次，在IES可靠性评估模型及算法方面：文献［9］将蒙特卡洛模拟法与故障模式影响分析法相结合，建立了并网和孤岛运行两种模式下的综合能源微网可靠性模型；文献［10］基于马尔可夫过程相关理论对系统设备状态变化进行建模，通过蒙特卡洛模拟法评估IES 可靠性水平；文献［14］建立了电-气互联IES 供电可靠性模型及其评估解析算法，但文献［9-10，14］均未考虑IES 的多时间尺度问题；文献［15］建立了考虑热负荷动态特性的IES 可靠性评估模型，通过基于马尔可夫链的序贯蒙特卡洛法评估了系统供能可靠性；文献［16］提出了适用于IES 优化调度的分层解耦方法，并将其与基于影响增量的状态枚举法相结合，对IES 可靠性水平进行了评估，但文献［15-16］均未充分考虑IES 中可再生能源出力不确定性和负荷需求响应等因素。

上述研究表明，IES 可靠性评估相关研究已受到国内外学者的广泛关注，但仍存在以下亟待解决的问题［17-19］：1）IES 中不同能源系统运行特性差异较大，需根据不同能源特性定义合理的可靠性指标以更准确地反映IES 可靠性水平；2）现有的可靠性评估模型及算法难以考虑IES 的多时间尺度问题，尤其是惯性较大的热力系统，热用户对供热中断的反应具有滞后性，且热用户的用能目的通常为获得满意的温度值或热舒适感，因此，需计及热负荷的上述特征提出IES 可靠性评估方法；3）IES 可靠性评估需充分考虑可再生能源出力不确定性和负荷需求响应等对系统可靠性的影响。

鉴于此，本文提出了计及用户热舒适度的IES可靠性指标及评估方法。首先，在负荷热惯性模型的基础上，从用户热舒适度的角度出发，建立了IES可靠性指标体系，包括负荷点可靠性指标和系统级可靠性指标；其次，在考虑可再生能源出力相关性及负荷需求响应的基础上，设置了计及用户热舒适度的负荷削减策略，提出了基于序贯蒙特卡洛模拟法的IES 可靠性评估方法及评估流程；最后，通过修改的IEEE 33 节点电力系统与天然气11 节点系统、热力32 节点系统经2 个能源集线器耦合而成的IES 进行算例仿真分析，验证了所提指标和方法的有效性。

1 计及用户热舒适度的IES 可靠性指标体系

1.1 热舒适度建模

1.1.1 负荷热惯性模型

IES 中不同能源系统的传输特性和时间尺度差异较大。相比于电、气负荷，热负荷的状态变化相对较慢，一般为小时级，其用能本质是在一段时间内保持温度在用户满意的区间，而不是固定的功率值［15］。因此，当设备故障导致供热中断时，用户对供热中断的反应具有滞后性，其在一定时间范围内的热需求仍可以得到满足，这一特性即为热惯性。以采暖建筑物这一热负荷为例，其热惯性模型可表示为［20］：

式中：c为采暖建筑物室内空气比热容；m为采暖建筑物室内空气质量；Tint为t时刻采暖建筑物室内温度；Qt为t时刻采暖建筑物总供热功率；Qenvt为t时刻采暖建筑物的围护结构热损失，与围护结构面积、围护结构热传导系数、室内外温度等有关；Qcolt为t时刻采暖建筑物的冷风渗透热损失，与冷风渗透量、室内外温度等有关；Qvent为t时刻采暖建筑物的通风热损失，与通风量、室内外温度等有关；Tint+1为t+1 时刻采暖建筑物室内温度；Δt为时间间隔。

1.1.2 用户热舒适度指标

热惯性模型体现了供热功率与热负荷温度之间的关系，但由于用户对环境热舒适度的感知具有模糊性，即当温度在一定范围内变化时，用户不会感受到明显的差异，因此，用户的采暖负荷需求是一个区间。目前，关于人体热舒适度的相关建模已有较多研究［21］，具体包括热感觉投票（thermal sensation vote，TSV）、标准有效温度（standard effective temperature*，SET*）、生理等效温度（physiological equivalent temperature，PET）、通用热气象指数（universal thermal climate index，UTCI）、预计平均热感觉指数（predicted mean vote，PMV）等。考虑到TSV 指标依赖于被调查者的主观投票，SET*指标的热舒适评价范围不包含“很冷”环境，PET 和UTCI 指标更适用于室外热舒适评价，本文选择PMV 指标来量化温度对用户热舒适度的影响。

PMV 值是以人体热平衡状态方程式为基础并考虑人体生理、心理学等因素来评价热舒适度标准的综合指标［22］。PMV 值表明群体对7 个等级热感觉投票的平均指数，PMV 为0 表明温度适中，PMV为-1、-2、-3 分别表示微凉、凉和冷，PMV 为+1、+2、+3 分别表示微暖、暖和热。PMV 值可通过下式计算得到［23］：

式中：M为人体新陈代谢率；η为人体机械做功效率；fcl为衣着系数，与服装热阻有关；hc为换热系数；Tcl为服装表面平均温度；Ta为室内空气温度；Rr为辐射散热量，与fcl、Tcl和环境平均辐射温度有关；E为包括呼吸不可测热损失量和皮肤出汗热损失量等的人体散热量。本文假设式中除室内空气温度Ta外，其他参数均为常数。

根据《民用建筑供暖通风与空气调节设计规范》，PMV 值宜处于［-1，+1］之间［22］。因此，通过热惯性模型求得热负荷在每个时刻的温度后，可根据式（3）求得对应的PMV 值，其值大小反映了用户热舒适度情况。在此基础上，便可从用户热舒适度的角度出发，建立IES 可靠性指标体系。

1.2 IES 可靠性指标体系

1.2.1 负荷点可靠性指标

1）负荷点故障率λ

式中：λj为负荷节点j的故障率；Tall为总模拟小时数；Nfj为在整个模拟时间段中负荷节点j的总故障次数。

对于电、气负荷，如果当前时间段内系统供能低于该负荷点负荷需求，则认为出现供电或供气故障；对于热负荷，通过式（1）和式（2）计算建筑物室内温度，如果温度低于最低允许温度则认为出现供热故障。其中，最低允许温度可根据PMV 指标进行设定，本文设置最低允许温度为PMV 值为-2，即体感为凉时所对应的温度值。

2）负荷点平均停供持续时间γ

式中：γj为负荷节点j的平均停供持续时间；Tfj为在整个模拟时间段中负荷节点j的总故障时间。

3）负荷点年平均停供持续时间U

VPMV，j(Xi)为系统在状态Xi下热负荷节点j处采暖建筑物的室内PMV 值，可通过式（3）计算得到。

1.2.2 系统级可靠性指标

选择系统平均停供频率（system average interruption frequency index，SAIFI）、系统平均停供持续时间（system average interruption duration index，SAIDI）、系统平均供能可靠率（average service availability index，ASAI）和系统供应不足期望（expected energy not supply，EENS）作为衡量电力系统、天然气系统、热力系统和IES 可靠性水平的指标［24］。其中，IES 整体的可靠性指标为各能源子系统可靠性指标的综合，可在负荷点可靠性指标的基础上，通过负荷点用户数加权得出，其具体计算方法如附录A 所示。此外，定义系统热用户满意度（system heat user satisfaction，SHUS）指标来衡量系统热用户处于热舒适的概率，由下式计算得到：

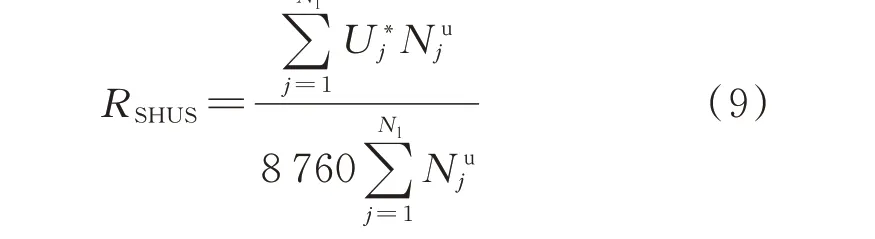
式中：RSHUS为系统热用户满意度；Nl为系统负荷节点总数；Nuj为负荷节点j处的用户数。

为衡量各种能源形式的耦合互联对系统可靠性水平的影响，定义系统可靠性提升率（system reliability improvement rate，SRIR）指标如下：

式中：RSRIR为系统可靠性提升率；R(0)为不同能源形式间无耦合互联时的系统级可靠性指标，包括SAIFI、SAIDI、ASAI、EENS 和SHUS；R为不同能源形式间存在耦合互联时的系统级可靠性指标。

综上，建立计及用户热舒适度的IES 可靠性指标体系如表1 所示。

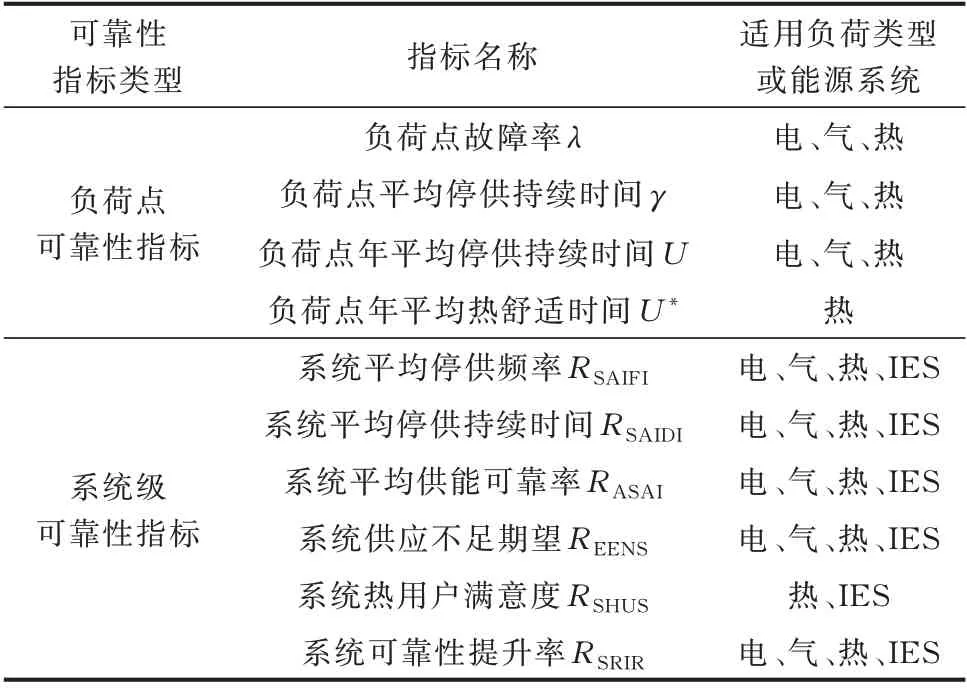
表1 IES 可靠性指标体系Table 1 Reliability index system of IES

2 IES 可靠性评估方法

考虑到IES 中可再生能源出力的不确定性以及负荷需求响应对IES 的运行状态有着不可忽视的影响，本章考虑可再生能源出力相关性以及需求响应，提出了基于序贯蒙特卡洛模拟法的IES 可靠性评估方法：通过序贯蒙特卡洛模拟法得到系统运行状态序列，依次对每个系统状态进行网络连通性分析，并根据网络连通状态，采用计及用户热舒适度的负荷削减策略进行负荷削减，以保证剩余负荷的正常供能。最后，总结了IES 可靠性评估流程。

2.1 可再生能源出力相关性处理

本文采用Nataf 变换生成具有相关性的可再生能源出力样本，其具体步骤如下所示［25］。

1）对于m维输入变量X=[X1，X2，…，Xm]T，其相关系数矩阵为ρ=(ρij)m×m，根据等概率原则将其转换为标准正态分布向量Y=[Y1，Y2，…，Ym]T，设Y的相关系数矩阵为ρ'=(ρ'ij)m×m。根据Nataf 的性质，(ρij)m×m与(ρ'ij)m×m的关系为：

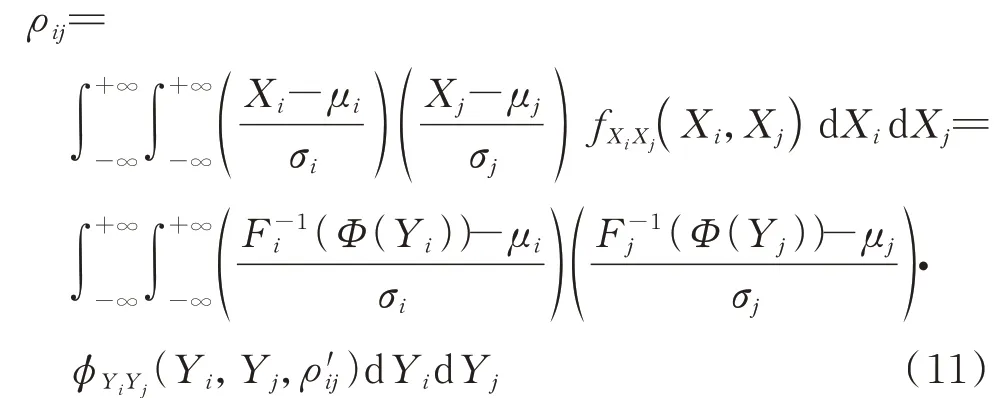
式中：μi和μj分别为随机变量Xi和Xj的均值；σi和σj分别为随机变量Xi和Xj的标准差；fXi Xj(Xi，Xj)为Xi和Xj的联合概率密度函数；Fi（·）和Fj（·）分别为随机变量Xi和Xj的累积分布函数；Φ（·）为标准正态分布的累积分布函数；ϕYiYj(Yi，Yj，ρ'ij)为相关系数ρ'ij的二维标准正态分布概率密度函数。考虑到上式求解较为复杂，为提高求解效率，本文采用文献［26］中的方法求取(ρ'ij)m×m。

2）对ρ'进行Cholesky 分解得到下三角矩阵G：

2.2 IES 需求响应建模

2.2.1 基于电价的需求响应机制

基于电价的需求响应主要通过设置峰谷分时电价来对用户的用能行为进行引导。通过引入电量电价弹性矩阵，实施峰谷分时电价后的用户用电量可由下式计算：

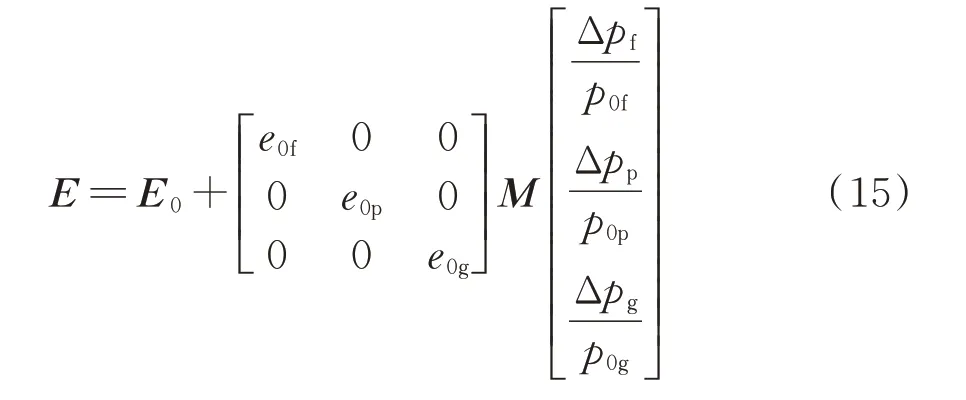
式中：E=[ef，ep，eg]T为实施分时电价后峰、平、谷时段的用电量；E0=[e0f，e0p，e0g]T为实施分时电价前峰、平、谷时段的用电量；M为电量电价弹性矩阵，其具体计算方法详见文献［27］；p0f、p0p、p0g分别为实施分时电价前峰、平、谷时段的电价；Δpf、Δpp、Δpg分别为实施分时电价前后峰、平、谷时段的电价变化量。

2.2.2 柔性负荷建模

柔性负荷可以灵活调节用能行为，缓解供需矛盾，对IES 的可靠性评估有着不可忽视的影响。本文主要考虑以下3 类柔性负荷：可平移负荷、可转移负荷和可削减负荷，其具体建模方法详见文献［28］，在此不再赘述。

2.3 基于序贯蒙特卡洛模拟法的IES 可靠性评估

2.3.1 序贯蒙特卡洛法仿真模型

假设系统所有元件均采用工作-故障两状态模型，元件的故障率和修复率分别为常数λ和μ，此时元件的无故障工作时间（time to failure，TTF）和修复时间（time to repair，TTR）均为服从指数分布的随机变量，可按式（16）和式（17）依次进行抽样［29］，形成元件运行状态持续时间序列，综合各元件可得到系统运行状态序列。

式中：TTTF为无故障工作时间；TTTR为修复时间；δ1和δ2分别为［0，1］上均匀分布的随机数。

选取评估指标的方差系数作为收敛判据，当所有评估指标的方差系数均小于给定值ε时认为程序收敛，其中ε一般取为0.03～0.08。方差系数具体计算方法为：

式中：βV为评估指标V的方差系数；σV为评估指标V的均值；μV为评估指标V的标准差；Nyear为模拟仿真年数。

2.3.2 IES 网络连通性分析

对蒙特卡洛模拟所得到的系统状态进行网络连通性分析，主要目的是分析系统中某一设备故障后，系统包含连通域的数量及每个连通域的构成情况。此处，采用节点标记法进行系统的连通性辨识。节点标记法通过依次搜索每条支路及其两端节点编号，将可以连通的节点划分为同一区域，完成所有支路的搜索后即可完成系统的连通性分析。

2.3.3 计及用户热舒适度的负荷削减策略

当IES 中设备出现故障导致系统不能完全满足所有负荷需求时，需要进行负荷削减以保证剩余负荷的正常供能［30］。本文通过定义负荷削减系数来确定负荷削减的优先顺序，综合考虑负荷所处位置和负荷重要程度，定义负荷削减系数如下式所示［31］：

式中：αi为负荷节点i的位置系数；di，sj为负荷节点i与电（气、热）源节点sj的最小距离，其与系统拓扑结构有关，相邻两负荷点距离为1；Ns为电（气、热）源节点总数；βi为负荷节点i的重要程度系数；Ii为负荷节点i的负荷削减系数，其值越小表示负荷削减优先级别越高。

基于上述负荷削减系数，设置计及用户热舒适度的负荷削减策略如下：对网络连通性分析后得到的所有连通域分别进行状态分析，若第k个连通域内能源供给不能完全满足所有负荷能源需求，则需根据负荷削减系数依次削减负荷，每完成一个节点的负荷削减工作后便重新进行功率平衡分析，直至第k个连通域内能源供给量不小于负荷量。

对于电负荷和气负荷，每次将负荷点处负荷削减至零。对于热负荷，本文基于负荷热惯性以及PMV 值来设置负荷削减策略，其基本原则是使负荷削减后的温度尽量不低于最低允许温度，即当要削减某一负荷点处的负荷时，先假设将此负荷点处负荷削减至零，通过式（1）和式（2）计算下一时刻温度，若下一时刻温度高于设置的最低允许温度，则将此负荷点处负荷削减至零；若下一时刻温度低于设置的最低允许温度，则将下一时刻温度设置为最低允许温度，通过式（1）和式（2）计算负荷功率，从而得到负荷削减功率。

计及用户热舒适度的负荷削减策略流程如图1所示。

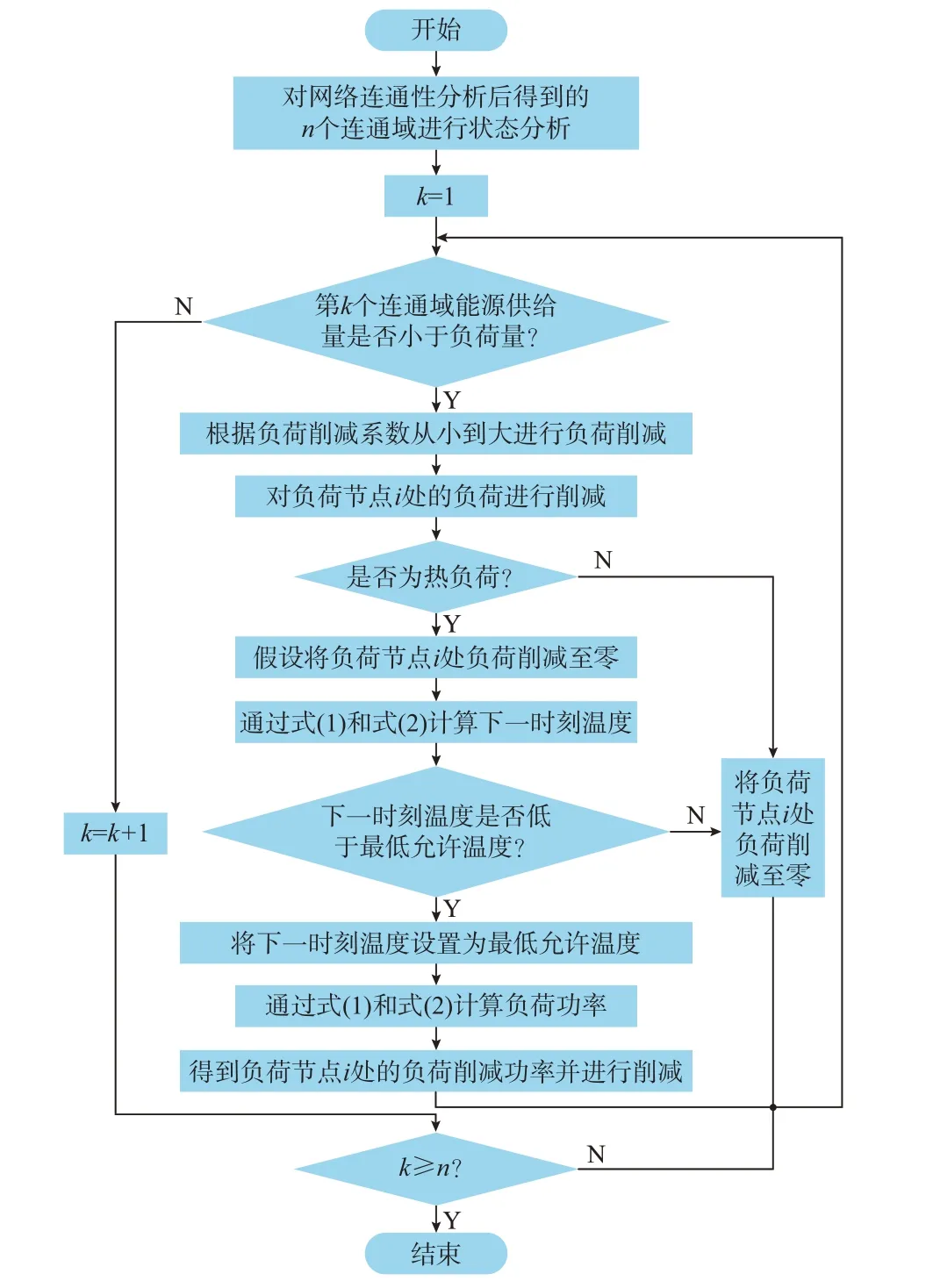
图1 计及用户热舒适度的负荷削减策略流程图Fig.1 Flow chart of load shedding strategy considering thermal comfort level of customers

2.4 IES 可靠性评估流程

综上所述，基于序贯蒙特卡洛模拟法的IES 可靠性评估流程具体步骤如下：

1）输入系统原始参数并进行数据初始化，设置仿真时间t=0，仿真年数Nyear=1。

2）随机产生与元件数量一致的随机数，根据式（16）求取每个元件的TTF。

3）选取TTF 最小的元件作为故障元件，得到系统的正常工作时间T=min(TTTF)，累计仿真时间t=t+T。

4）再产生一随机数，根据式（17）求取故障元件的TTR，作为系统故障持续时间。

5）采用节点标记法对网络进行连通性分析，分析系统包含连通域的数量及每个连通域的构成。

6）判断系统中可再生能源出力是否具有相关性，若是，则通过Nataf 变换生成具有相关性的可再生能源出力样本，否则进入下一步。

7）首先，对故障设备所处的子系统进行状态分析，若区域内能源供给量为零，则区域内所有负荷均得不到能源供给；若能源供给量不为零且不小于负荷量，则无须进行负荷削减；若能源供给量不为零且小于负荷量，则基于计及用户热舒适度的负荷削减策略，对区域内负荷进行削减，直至能源供给量大于等于负荷量。

8）判断故障是否通过能源耦合设备影响到其他能源子系统，即判断能源集线器的输入、输出量是否发生变化，对其他能源子系统进行状态分析。

9）对于热负荷节点，通过式（1）和式（2）计算下一时刻温度。

10）累计负荷点故障时间、故障次数和热舒适时间，累计仿真时间t=t+T+TTTR。

11）判断仿真时间t是否大于仿真年数Nyear，若是，则进入下一步，否则返回第2）步。

12）计算负荷点、系统级可靠性指标，判断可靠性指标是否收敛，若是，则进入下一步，否则Nyear=Nyear+1，返回第2）步。

13）输出负荷点、系统级可靠性指标计算结果，对IES 可靠性水平进行评估。

IES 可靠性评估流程图见附录A 图A1。

3 算例分析

3.1 算例概况

本文采用修改的IEEE 33 节点电力系统与天然气11 节点系统、热力32 节点系统经2 个能源集线器耦合而成的IES 进行算例仿真分析。其中，在修改的IEEE 33 节点电力系统中，节点EB18、EB22、EB25 和EB33 各配置一台光伏机组。算例系统拓扑结构如附录B 图B1 所示，其中，虚线为电力系统联络线，天然气系统和热力系统参数见文献［32-33］，采暖建筑物热惯性方程相关参数见文献［20］，PMV 计算方程相关参数见文献［23］，能源集线器参数及光伏机组参数如附录B 表B1、表B2 所示。

假设不同设备的故障相互独立，并且只考虑单重故障的情况［9］，故障元件包括变压器、光伏机组、配电线路、气源、天然气管道、热源、热力管道以及能源转换设备，系统元件可靠性参数参照文献［9，16］，其具体取值如附录B 表B3 所示。实施分时电价前后的负荷（以节点EB7 为例）曲线如附录B 图B2 所示，由图可知分时电价的实施起到了削峰填谷的作用。此外，设置节点EB20 为可削减负荷、节点EB28 为可平移负荷、节点GB6 为可转移负荷。设置采暖建筑热负荷最低允许温度为18 ℃（在本算例参数设置下PMV 值为-2 时对应的温度值），最高温度为25 ℃，热负荷温度仿真步长Δt为1 h，热负荷在一天内的温度变化如附录B 图B3 所示。由图可知，由于负荷热惯性的存在，使得用户对供热状态的感知滞后于设备状态的改变。仿真收敛条件为系统级可靠性指标的方差系数小于0.05。

3.2 算例结果分析

3.2.1 可靠性指标分析

采用本文所提的IES 可靠性评估方法对上述算例进行仿真分析。负荷点可靠性指标计算结果如附录C 图C1—图C3 所示，系统级可靠性指标计算结果如表2 所示。

表2 系统级可靠性指标计算结果Table 2 Calculation results of system-level reliability indices

表中可靠性指标计算结果表明：

1）电力系统、热力系统与天然气系统中，系统平均停供持续时间RSAIDI和供应不足期望REENS逐渐增大，系统平均供能可靠率RASAI逐渐减小，说明电力系统可靠性水平最高，热力系统次之，天然气系统可靠性水平最低。

2）相比于电力系统和天然气系统，热力系统平均停供频率RSAIFI较小，分析其原因如下：系统故障时采用了计及用户热舒适度的负荷削减策略进行负荷削减，并且选择温度而不是功率作为热负荷故障的判断标准，导致热力系统会出现功率削减后仍然满足热需求的情况，使得负荷点故障率降低。

3）3 个能源子系统和IES 整体的平均供能可靠率RASAI均在99%以上，系统热用户满意度RSHUS为99.905%，可靠性水平较高但仍有提升空间。

3.2.2 光伏出力相关性对系统可靠性的影响

为了验证光伏出力相关性对系统可靠性的影响，设置不同光伏机组的出力相关系数均相同。相关系数分别为0.01、0.50、0.99 时，电力系统负荷点平均停供持续时间γ如图2 所示，电力系统和IES 整体的系统级可靠性指标如表3 所示。通过图2 可以看出，随着光伏出力相关系数的增大，电力系统负荷点平均停供持续时间γ呈降低趋势，可靠性水平升高。进一步通过表3 可以看出，光伏出力相关系数增大，电力系统和IES 整体可靠性水平上升，与图2结果相吻合。

表3 不同光伏出力相关系数下电力系统和IES 系统级可靠性指标Table 3 System-level reliability indices of power system and IES with different correlation coefficients of photovoltaic output

图2 不同光伏出力相关系数下的电力系统负荷点可靠性指标γFig.2 Load-level reliability index γ of power system with different correlation coefficients of photovoltaic output

分析其原因如下：相比于负荷水平而言，系统光伏机组容量较小，当光伏出力相关系数较小时，不同光伏机组出力差别较大，只要个别光伏机组出力偏低便会导致供电不足，使得可靠性水平偏低；当光伏出力相关系数较大时，光伏机组同时出力偏高的可能性增加，有利于可靠性水平的提高。此外，由于系统中存在电转热设备，电力系统可靠性水平上升进而导致热力系统可靠性水平上升；电力系统和热力系统可靠性水平的升高导致IES 整体可靠性水平上升；而系统中没有电转气等电能转换成天然气的装置，电力系统可靠性水平升高不会对天然气系统产生明显影响。

3.2.3 负荷削减策略对系统可靠性的影响

设置2 种不同的负荷削减策略：一种是本文2.3.3 节提出的计及用户热舒适度的负荷削减策略，即对热负荷进行削减时，以下一时刻温度不低于最低允许温度为准则进行削减；另一种是不计及用户热舒适度的负荷削减策略，即对热负荷进行削减时，与电负荷和气负荷相同，直接将负荷功率削减至零。2 种情况下热力系统负荷点故障率λ计算结果如图3 所示，热力系统和IES 的系统级可靠性指标计算结果如表4 所示。

通过图3 可以看出，相比于计及用户热舒适度的负荷削减策略，不计及用户热舒适度时负荷点故障率λ呈增大趋势，说明可靠性水平降低。进一步从表4 可以看出，当采取计及用户热舒适度的负荷削减策略时，热力系统及IES 的可靠性指标计算结果更优。因此，当IES 发生故障时，采取恰当的负荷削减策略对系统可靠性水平评估结果有提升作用。

图3 不同负荷削减策略下的热力系统负荷点可靠性指标λFig.3 Load-level reliability index λ of heating system with different load shedding strategies

表4 不同负荷削减策略下热力系统和IES 系统级可靠性指标Table 4 System-level reliability indices of heating system and IES with different load shedding strategies

3.2.4 需求响应对系统可靠性的影响

为了验证需求响应对系统可靠性的影响，设置以下2 种场景：场景1 考虑需求响应，包括基于电价的需求响应机制和柔性负荷；场景2 不考虑需求响应。2 种场景下的电力系统负荷点年平均停供持续时间U如图4 所示，电力系统和IES 的系统级可靠性指标计算结果如表5 所示。

图4 需求响应对电力系统负荷点可靠性指标U 的影响Fig.4 Effect of demand response on load-level reliability index U of power system

由图4 可见，不考虑需求响应时电力系统负荷点年平均停供持续时间U呈增大趋势，柔性负荷节点EB20 和EB28 的年平均停供持续时间U有较大幅度增加，可靠性水平降低。进一步从表5 可以看出，考虑需求响应有利于提高系统的可靠性水平。

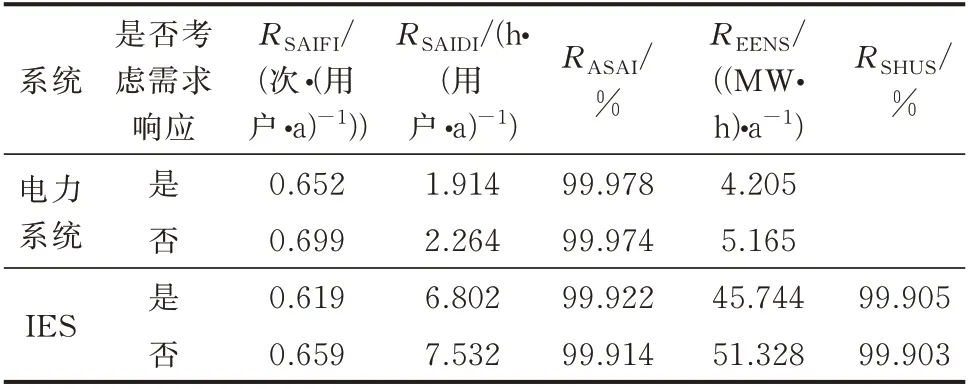
表5 需求响应对系统级可靠性指标的影响Table 5 Effect of demand response on system-level reliability indices

3.2.5 耦合互济对系统可靠性的影响

为了验证IES 中不同能源子系统的耦合互济对系统可靠性的影响，设置以下2 种场景：场景1 中IES 不存在耦合互济，即能源集线器容量为0；场景2 中IES 存在耦合互济，能源集线器参数与3.1 节相同。2 种场景下IES 系统级可靠性指标计算结果如表6 所示。通过表6 可以看出，相比于各能源子系统单独运行，耦合互济运行有利于充分利用各类能源以提升系统的可靠性水平，且系统热用户满意度RSHUS有所提高，用户热舒适感提升；通过不同系统级可靠性指标计算的系统可靠性提升率从不同角度体现了能源耦合互济对系统可靠性水平的影响程度。