针对机动目标的三维实时滚动优化制导策略
2023-02-01杨秀霞姜子劼
杨秀霞, 姜子劼, 张 毅, 王 聪
(海军航空大学, 山东 烟台 264001)
0 引 言
飞行器制导(导引)律是根据目标的位置、速度等状态信息,引导飞行器接近目标,实施拦截的技术手段,是实现精确打击或拦截导引的火控系统关键技术之一[1],制导律设计是否合理对飞行器能否精准拦截目标起到了至关重要的作用。
比例导引律由于形式简单、导引精度高等诸多优点,是目前应用最为广泛的制导律[2-4],它通过在飞行器上施加过载,抑制视线旋转,从而实现制导。Yang等[5]通过对描述相对运动的3个耦合非线性二阶状态方程进行解析求解,推导了拦截非机动目标和小机动目标的三维真比例导引律,当目标不机动且飞行器与目标的速度为常值时,该制导方法被证实为一种最优制导律[6],而当目标具有强机动性时,比例导引律的制导性能将急剧下降[1]。
对此,研究人员纷纷提出改进措施,滑模变结构制导律[7]、自适应模糊制导律[8-9]等新型制导律应运而生,与此同时,最优导引律也因为能够解决带状态约束的制导问题,而获得了更为广泛的应用。最优导引律以最优控制理论为基础,根据飞行器制导的实际情况,将包括终端脱靶量、制导时间、能量消耗在内的诸多性能指标纳入考虑,并通过优化性能函数得到具有最优性能的导引律。Kishi等[10]首次将最优控制理论应用到制导律设计当中,其后Hughes等[11]、Rusnak等[12]学者纷纷效仿,并对攻击角约束、加速度约束下的制导问题展开研究[13-14]。目前,基于线性二次型最优理论的导引律已进入实用阶段。但是,由于全局优化的最优导引律要求目标运动信息全部已知,这对飞行器的测量元件而言是难以实现的,并且,由于制导过程中需要实时估计终端时刻,这在目标运动加速度信息未知的条件下亦是极为困难的,因此部分学者开始将目光投向局部最优导引律。
局部最优导引律采用滚动式的有限时域优化策略。与全局最优导引律不同,局部最优导引律的优化过程不是一次离线完成的,而是通过优化相对于某一时刻的局部性能指标,得到从该时刻起到未来有限时间的最优导引律,并且随着时间反复不断地进行在线优化,直到完成制导过程。这一方法的优势在于无需估计终端时间,仅需要对未来一段时间内的未知信息进行预测,同时由于能够实时地进行反馈校正,因而具有较强的鲁棒性。但是,在无法求得最优控制解析解的情况下,采用迭代法求解最优控制数值解是一项耗时的工作,如果不需要在每一个时域内反复求解最优控制,局部最优导引律将取得更广泛的应用。
近年来,随着机器学习技术不断发展,各领域都在尝试与之进行结合,不少学者也在飞行器制导领域进行了相关探索,Li等[15]基于模型预测控制理论,在有限时域上利用原始-对偶神经网络求解约束二次规划问题,并利用其在线解实时做出制导决策;Shao等[16]利用径向基函数神经网络实时估计目标信息,减少三维运动模型中的耦合干扰;Liang等[17]基于模型预测路径积分控制,提出了一种适用于执行器失效情况下的深度强化学习制导方案;刘扬等[18]通过对制导问题的状态和动作进行设计,实现了从环境交互数据中学习回报最优的制导决策。
受此启发,为了解决目标机动策略未知条件下的三维空间制导问题,本文在滚动时域优化框架下提出了基于深度神经网络(deep neural networks, DNN)的实时制导策略。首先,用零效脱靶量(zero effort miss, ZEM)代替相对距离作为局部终端指标,改进性能函数,利用极小值原理推导性能函数最小化的必要条件,并设计粒子群优化算法求解有限时域内的最优控制;其次,针对目标可能采取的若干种随机机动形式,利用粒子群优化算法分别进行滚动优化求解,提取求解过程中产生的状态量、控制量,组成网络训练样本数据,对DNN进行离线训练,使经过训练的网络能够根据状态输入自行解算制导指令;再次,针对目标角速度等状态信息难以直接观测的问题,利用单隐含层神经网络对目标历史运动状态进行时序分析,在线预测目标未来运动状态;最后,将飞行器当前状态、目标未来状态预测结果组成特征向量,输入DNN,实时输出飞行器制导指令。仿真实验结果表明,相较于传统制导律,本文设计的制导策略具有更好的制导性能,且提升了局部最优导引律的在线优化效率,可以为基于数据和学习方式的飞行器制导指令实时解算提供参考和支持。
1 问题描述与建模
1.1 问题描述与模型假设
本文主要研究单个飞行器对单个机动目标的三维拦截制导问题,主要性能判据为(全局)终端脱靶量和飞行器能量消耗。在制导律推导过程中做出如下假设:
(1) 飞行器控制系统具有理想动态特性,信息传输及控制指令传递无延迟;
(2) 飞行器与目标在运动过程中可视为质点,二者速度均为常值;
(3) 飞行器与目标运动可在水平面与铅垂面解耦。
1.2 系统状态方程及优化模型建立
在三维制导问题中,飞行器与目标的运动学方程分别为
(1)
(2)

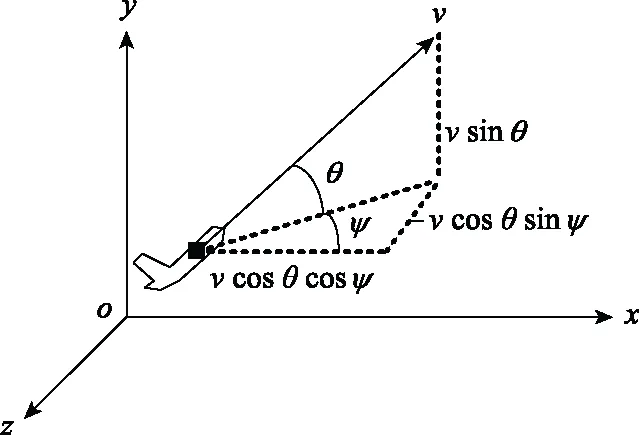
图1 飞行器(目标)三维运动示意图Fig.1 Three dimensional motion diagram of aerocraft (target)
设控制量:
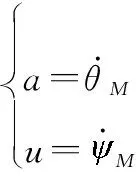
令:
(3)
则制导系统状态方程为
(4)
式中:

实现精准快速的拦截是飞行器制导的首要目的。而在拦截大机动高速目标时,飞行器通过不断地调整控制指令、纠正自身航向,来保证始终处于拦截目标的有利态势,这一过程往往伴随着大量的能量消耗,因此能否对能量进行动态高效的分配与管理,也是维持与保证飞行器制导效果的关键所在。出于以上考虑,将制导过程中的能量损耗作为积分指标,把终端脱靶量作为终端指标,设计制导问题的全局性能函数:
(5)
式中:tf为制导终止时刻。

2 粒子群-滚动时域优化方法
2.1 滚动时域优化框架
滚动时域优化将整个控制时域[t0,tf]分隔为若干控制周期与预测周期。其中,预测周期TP是能够较为准确地预测目标运动状态的时间周期,该周期的主要任务为预测和优化,即利用目标先前的运动信息,对目标倾角速度、偏角速度等难以观测获得的信息进行预测,并借助预测结果,通过优化性能函数,确定飞行器在τ∈[t,t+TP](t为当前时刻)的最优控制序列a*(τ),u*(τ);控制周期TC为飞行器进行滚动控制的时间周期,该周期的主要任务为控制与反馈,即将最优控制序列中τ∈[t,t+TC]的部分作为实际控制指令作用于飞行器,实时反馈并观测双方状态信息。完成当前控制周期后,即进入下一控制周期,并同时基于更新反馈的状态信息进行新一轮预测和优化。如此循环,直到制导过程终止。该方法伪代码如下:
t=t0
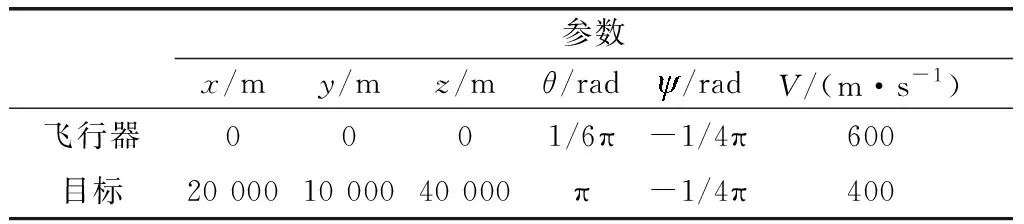
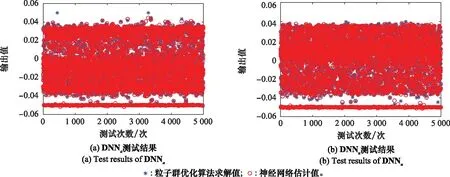
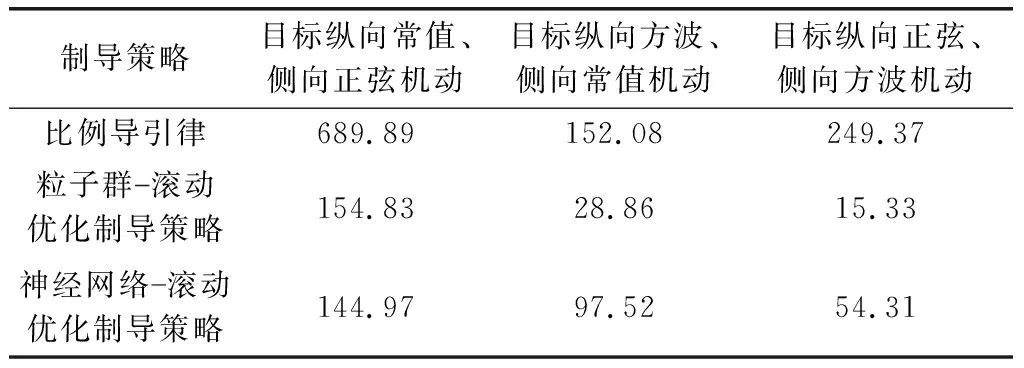
whilet solve minJ(t,TP) geta*(t),a*(t+Δt),…,a*(t+TP); u*(t),u*(t+Δt),…,u*(t+TP) a(t)←a*(t) ⋮ a(t+TC)←a*(t+TC) u(t)←u*(t) ⋮ u(t+TC)←u*(t+TC) t←t+TC End while 其中,Δt为采样时间;TC,TP取为Δt的正整数倍。 关于滚动时域优化方法,还有以下两点需要说明: (1) 不论采取何种预测方式,对于目标未来状态的预测结果均会存在偏差,因此依赖于预测结果获得的控制序列并非完全可靠,如果将其全部作用于飞行器,将会影响控制的精度。所以在TP与TC之间,通常有TP>TC; (2) 在预测周期以外,由于无法准确地预测目标未来状态,亦无法通过优化性能函数求解飞行器最优控制指令,因此参照文献[19],基于当前时刻t做出如下假设: 假设2当时间τ>t+TP时,对飞行器停控,即控制量a、u均为0。 在滚动时域优化框架下,全局最优制导问题式(5)被分解成多个子问题,这样一来,每一个子问题的初始时刻和终端时刻便能固定下来(初始时刻即当前时刻t,终端时刻为t+TP),那么仅需对每一个具有相同形式的子问题进行优化求解,便能最终获得全局制导问题的解。 由于目前所能查阅的文献仅给出了二维平面ZEM的计算公式,因此需对三维空间ZEM表达式进行推导。 根据文献[20]得到二维平面上ZEM的计算公式: (6) 式中:r表示飞行器与目标的相对距离;q表示飞行器与目标的视线角。用第1.1节所设状态量,对xoy面的ZEMxoy进行描述: (7) 对qxoy和rxoy求导,得到 (8) (9) 将式(8)、式(9)代入式(7),得到 (10) 再对ZEMxoy取平方,并将其转化为如下形式: (11) (12) (13) 据此,设计局部终端指标: (14) 改进后的局部性能函数为 (15) 一般来说,在整个制导过程中,飞行器与目标的相对距离持续减小,即飞行器与目标的相对速率始终为负,直至飞行器与目标的相对速率符号转变瞬间,制导过程结束。此外,考虑到飞行器的动力学特性,对其倾角速度与偏角速度施加边界约束。因此,制导问题的约束条件为 (16) 根据式(15),列写Hamilton函数: H(x,a,u,λ,τ)=a2(τ)+u2(τ)+λTf(x,a,u,τ) 式中:λ(τ)为拉格朗日乘子向量函数: λT(τ)=[λ1(τ),λ2(τ),…,λ6(τ)] f(x,a,u,τ)=Ax(τ)+B1(τ)a(τ)+B2(τ)u(τ)+ 得到协态方程: (17) 横截条件 (18) 式中: K(t+TP) 另外,由庞特里亚金极小值原理可知,在最优控制[a*(τ),u*(τ)]上,Hamilton函数取极小值。对H(x,a,u,λ,τ)求其关于a(τ),u(τ)的导数及二阶导数: (19) 不难看出,当控制量a(τ),u(τ)不受边界约束的条件,H(x,a,u,λ,τ)在 (20) (21) (22) (23) 至此,我们已经获得了使性能函数J取极小值的全部必要条件,下面只需确定协态变量即可算出有限时域内的局部最优控制。 一般情况下,对于如式(15)所示的优化问题,我们很难得到其解析解表达式,此时往往需要采用数值方法求解。梯度法、共轭梯度法等直接方法是计算该类问题的通用范式,这类方法采取双向积分方式,计算过程稳定,但也存在易落入局部最优、接近最优解时收敛过缓等缺陷。而边界迭代法等间接方法涉及复杂的求逆运算,较易引入误差,进而影响最优控制的求解精度。对此,提出一种基于粒子群优化算法的求解策略,该策略通过更新粒子飞行速度完成迭代,迭代过程中,粒子既可利用自身寻优的历史信息,还可向优秀粒子学习,从而避免局部收敛。此外,该算法无需大量的求梯度、求逆运算,易于实现的同时保证了求解精度。 首先,对协态方程式(17)求其关于时间τ的积分,得到 (24) 基于粒子群优化算法求解最优控制的具体步骤描述如下: 步骤3根据横截条件式(18)定义误差向量为 (25) 适应度函数采用误差向量的2-范数与性能函数之和的形式,定义为 (26) 步骤5更新粒子位置 (27) 更新粒子速度 (28) 其中,超参数wmax,wmin表示最大、最小惯性权重。相比于定值惯性权重,自适应惯性权重的优势在于能够根据粒子适应度调整搜索方式:当粒子适应度大于种群平均适应度时,其惯性权重越大,越有利于粒子跳出局部最优值进行全局搜索;反之,当粒子适应度小于种群平均适应度时,其惯性权重越小,越有利于粒子对当前区域进行精细的局部搜索。 步骤7根据粒子适应度,选出个体最优粒子和全局最优粒子,并进入下一次迭代。 步骤8迭代终止,输出cbest=[c1best,c2best,…,c6best]T,根据式(22)和式(23)计算最优控制序列a*(τ),u*(τ)(t≤τ≤t+TP)。 至此,我们通过粒子群优化算法,在滚动时域优化框架下,得到了局部最优控制的数值解序列。但是对于状态变换迅速、攻防对抗激烈的制导问题而言,如果在每一个控制周期都通过此类数值迭代方法求解最优控制,虽然能够保证足够的求解精度,但却会耗费大量计算时间,从而造成控制延迟甚至失效。 为了满足制导指令实时规划的要求,利用DNN强大的泛化能力,提出一种制导指令在线生成的智能制导策略。 通过粒子群优化算法求解局部最优控制,为制导问题提供了一种解决方式,如果这种方式被保留下来,用以指导实际任务中的制导指令在线生成,将会大大提高制导指令的解算精度。神经网络是一种进行分布式并行信息处理的算法,通过对网络结构和训练方式的合理设计,理论上可以使其逼近任意复杂的算法或模型。如果将神经网络应用于实际制导过程中,通过一组输入即可使其输出容许范围内的最优控制,那么制导指令的解算效率也将获得大幅提升。 基于上述考虑,本节利用具有多隐含层的DNN对粒子群优化算法滚动求解得到的大量样本数据进行离线学习,使之模仿飞行器动态决策行为,再将经过学习的网络用于制导指令的在线生成。通过这种方式获得制导指令,无需在每个控制周期反复地迭代求解最优控制,从而提高了指令生成速度,且能够充分利用粒子群优化算法的求解信息,保证了指令求解精度,因此更适合作为一种在线制导策略。 离线学习是指对独立的数据进行训练,再将训练得到的模型用于预测任务中的机器学习方式,其目的是使神经网络更好地逼近实际模型,且在遇到新任务时具有较强的泛化能力。 3.1.1 样本数据采集 为了使神经网络适应目标可能采取的各种机动行为,基于几种常见的随机信号生成若干组目标倾角速度、偏角速度时间序列,根据式(1)得到若干目标运动状态。 (29) (30) 其中,输入矩阵行数为10,列数为样本数量,记为Ns。 3.1.2 DNN构建 神经网络由输入层、隐含层及输出层构成,为了使神经网络更好地逼近实际模型,通常要基于实测数据对各种可行的网络结构及训练方式进行测试和对比,并从中选择拟合程度较高、泛化能力较好的网络模型应用于实际问题。 网络结构由神经网络层数和隐含层神经元个数共同决定,对于复杂模型来说,一般要通过隐含层数大于1的DNN进行学习,而在不增加隐含层数的情况下,盲目增加神经元数量并不会使网络性能得到太大提升。 训练方式取决于激活函数和优化算法。常用的激活函数有S型生长曲线函数(Sigmoid)、双曲正切函数(tanh)以及线性整流函数(ReLU)等,而常用的优化算法主要包括梯度下降法、牛顿算法、共轭梯度法以及Levenberg-Marquardt算法等。 通过采用不同的网络结构及训练方式对第3.1.1节获得的样本数据进行学习发现,当隐含层数量为5时网络拟合程度较高,采用tanh作为激活函数,Levenberg-Marquardt作为优化算法时训练速度较快、性能较好。此外,为了保证预测精度,以控制量a与u作为输出分别构建DNNa与DNNu。 3.1.3 离线学习 下面以控制量a作为输出的神经网络DNNa为例,介绍网络离线学习过程。 将a′转置后作为实际输出,即网络输出目标值: Sout=[a′]T (31) 每一隐含层的神经元个数分别设为nhi(i=1,2,…,5)。于是可以确定权值、阈值矩阵维数:W1nh1×10,W2nh2×nh1,…,W5nh5×nh4,W61×nh5,B1nh1×1,B2nh2×1,…,B5nh5×1,B61×1。 激活函数采用tanh: 定义矩阵运算s(A)=[tanh(aij)]m×n,其中A=(aij)m×n,于是网络前向传递过程可以描述为 H1out=s(W1Sin+B111×Ns) Hi+1 out=s(Wi+1Hi out+Bi+111×Ns),i=1,2,3,4 Nout=W6H5out+B611×Ns (32) 式中:1m×n表示元素全为1的m×n维矩阵;Hi out表示第i层隐含层输出;Nout表示网络输出。 定义误差向量: E=Sout-Nout (33) 损失函数: (34) 网络训练的目的是使网络输出值尽可能逼近目标值,即通过更新网络参数,使L(E)<ε,其中ε为一较小正值。为了使损失函数收敛,传统的梯度下降法基于梯度进行参数更新,从几何意义上讲,梯度代表函数增加最快的方向,因此沿着与之相反的方向便可以更快地找到损失函数的极小值。而不同于传统的梯度下降算法,Levenberg-Marquardt算法不仅能够找到函数下降的方向,还能合理地决定参数更新的速度,因此收敛速度快、收敛性好。 如果将神经网络的某一参数矩阵铺陈为nw维向量w,则基于Levenberg-Marquardt算法的参数更新方式为 (35) 式中:Jw表示误差(向量)E关于参数(向量)w的Jacobian矩阵: 基于Levenberg-Marquardt算法的反向传播过程描述如下: 步骤1随机生成网络权值矩阵、阈值矩阵; 步骤2当迭代次数小于最大迭代次数时执行步骤3和步骤4,否则转步骤5; 步骤3根据式(32)~式(34)计算损失函数,当损失函数小于预设值时,转步骤5; 步骤4根据式(35)更新网络参数,进入下一次迭代并转步骤2; 步骤5终止迭代,输出网络权值、阈值。 在完成网络训练之后,最终可以获得最优网络参数,当新的一组状态量输入网络时,即可通过式(32)计算网络输出。 至此,利用粒子群优化算法求解得到的大量样本数据,完成了基于DNN的制导指令生成器的设计。而在实际制导过程中,能否取得良好的制导效果不仅取决于生成器设计是否合理,还极大地依赖于对于目标运动状态的估计是否准确。下面,基于浅层神经网络,设计目标倾角、偏角速度的在线估计器。 由于目标倾角、偏角速度无法通过直接观测获得,因此在基于滚动时域优化的制导过程中,如果能够准确地预测两者的大小,将会极大地解决由于预测偏差引发的系统失稳等问题。一般来说,目标在某一时刻的机动指令并非完全随机的,而是具有某些时间相关的变化特点,因此可通过分析目标运动状态的历史信息,预测其未来的运动状态。而神经网络作为一种通用的状态估计器,同样可以用于目标机动指令的时序分析与预测。为了兼顾预测精度和预测效率,基于单隐含层神经网络设计目标倾角、偏角速度的在线估计器。 首先,将目标倾角、偏角速度的历史信息组成网络训练样本数据。以目标倾角速度为例,设当前时刻为t,历史信息数量为m+n-1,则样本数据矩阵为 (36) 网络激活函数仍采用tanh,训练过程采用基于Levenberg-Marquardt的反向传播算法。由于上文已对该方法进行过详细描述,此处不再赘述。 在t+Δt时刻到来时,则以t+Δt时刻为当前时刻,更新网络训练样本数据,训练神经网络并产生新的预测值。 经过离线训练的神经网络可以根据当前状态直接输出制导指令,而无需考虑控制输出延迟,因此为了充分利用双方状态的实际测量值,提升制导精度,把控制周期设定为采样时间Δt。 至此,完成了制导指令在线生成的智能制导策略设计,下面通过算例对该制导策略的性能进行仿真验证。 本文设定的实验场景为目标初始位置、倾角、偏角以及飞行器初始位置、倾角、偏角已知,并且目标的位置、角度可实时获取,目标机动策略未知且具有一定的随机性。在制导过程中,飞行器制导指令延迟不做考虑。 飞行器与目标的初始状态参数如表1所示。 表1 飞行器-目标初始状态参数 基于随机信号形成500组目标机动指令序列,根据初始状态参数及状态方程式(1)获得各组目标运动状态。设定预测周期为0.5 s,控制周期为0.1 s,利用粒子群-滚动时域优化算法对每组目标求解最优控制序列,生成20余万组网络训练样本数据。飞行器分别对具有不同机动形式的目标实施拦截的三维运动轨迹如图2所示。 图2 对具有不同机动形式的目标实施拦截的三维轨迹Fig.2 Three dimensional trajectories of intercepting targets with different maneuver forms 按照97.5%、2.5%的比例将样本数据划分为训练集与测试集,利用训练集分别对DNNa和DNNu进行离线训练。网络性能函数随训练次数的变化情况如图3所示。分别经过406次与603次训练,网络输出误差达到预设要求。利用测试集测试网络训练效果,测试结果如图4所示。 图3 神经网络离线训练情况Fig.3 Off-line training of neural network 图4 神经网络测试结果Fig.4 Test results of neural network 从随机常值机动、随机正弦机动、随机方波机动中任取两种分别作为目标在纵向和侧向的机动方式,对神经网络-滚动时域优化制导策略的制导效果进行检验。 选取的目标机动方式为:(a)纵向常值机动、侧向正弦机动;(b)纵向方波机动、侧向常值机动;(c)纵向正弦机动、侧>向方波机动。 针对上述3种组合机动方式,利用神经网络-滚动优化制导策略对目标实施拦截,设定预测周期为0.5 s,控制周期为0.1 s。飞行器对目标运动状态的滚动预测结果如图5~图7所示。 图5 目标运动轨迹预测情况Fig.5 Prediction of target trajectory 图6 目标倾角预测情况Fig.6 Prediction of target inclination angle 图7 目标偏角预测情况Fig.7 Prediction of target deflection angle 将神经网络-滚动优化制导策略的制导效果与三维比例导引律以及粒子群-滚动优化制导策略(预测周期为0.5 s,控制周期为0.1 s)进行对比,得到仿真结果如图8~图11所示。 图8 飞行器-目标三维运动轨迹Fig.8 Three dimensional trajectory of aerocraft and target 图9 飞行器-目标二维运动轨迹(目标纵向常值、侧向正弦机动)Fig.9 Two dimensional trajectory of aerocraft and target(target longitudinal constant and lateral sinusoidal maneuver) 图10 飞行器-目标二维运动轨迹(目标纵向方波、侧向常值机动)Fig.10 Two dimensional trajectory of aerocraft and target(target longitudinal square wave and lateral constant maneuver) 图11 飞行器-目标二维运动轨迹(目标纵向正弦、侧向方波机动)Fig.11 Two dimensional trajectory of aerocraft and target(target longitudinal sinusoidal and lateral square wave maneuver) 图12 飞行器-目标相对距离变化情况Fig.12 Relative distance between aerocraft and target 观察飞行器-目标运动轨迹发现,由于能够较为准确地预测目标运动信息,采取神经网络-滚动优化制导策略与粒子群-滚动优化制导策略的飞行器提前针对目标机动行为做出反应,并且较快地接近目标。图12表明,针对上述3种机动目标,神经网络-滚动优化制导策略与粒子群-滚动优化制导策略均能够引导飞行器以较小的终端脱靶量完成拦截。 在优化效果上,采取3种制导策略对上述3种目标实施拦截的性能指标(式(5))如表2所示。 表2 利用3种制导策略分别实施拦截的性能指标 可以看出,神经网络-滚动优化制导策略的优化效果介于粒子群-滚动优化制导策略与比例导引律之间,但是在计算时间上,利用神经网络-滚动优化制导策略生成制导指令平均耗时少于0.01 s,而利用粒子群-滚动优化制导策略生成制导指令平均耗时0.47 s,显然,神经网络-滚动优化制导策略大大提升了制导指令生成速度,相较于后者,更能满足制导拦截任务的实际需要。 本文针对三维空间内目标机动策略未知条件下的制导拦截问题,基于滚动时域优化理论和神经网络设计了一种制导指令在线实时规划方案,并通过仿真实验初步表明该方案具有良好的制导性能,可以为基于数据和学习方式的飞行器制导指令在线规划提供参考和支持。在此后的工作中,考虑把本文的研究方法应用于多飞行器协同拦截制导问题,寻求一种基于机器学习的多飞行器协同智能制导方案。
2.2 基于ZEM的最优制导问题


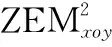


2.3 最优制导问题的粒子群优化算法







3 基于神经网络的滚动优化制导策略
3.1 神经网络构建及离线学习



3.2 目标倾角、偏角速度在线滚动预测


3.3 实时滚动优化制导策略设计

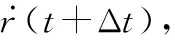
4 仿真实验与分析











5 结 论
