基于合作目标的外辐射源雷达发射站直接定位
2023-02-01饶云华朱华梁郑志杰
饶云华, 朱华梁, 郑志杰
(武汉大学电子信息学院, 湖北 武汉 430072)
0 引 言
外辐射源雷达利用第三方发射站(如广播电视等)发射的信号作为照射源对目标进行探测定位,具有抗干扰能力强、隐蔽性好等优点,受到学者们的广泛关注[1-4]。外辐射源通常为带宽较宽的连续波信号,有利于对目标进行精细化探测,占伟杰等[2]利用数字电视外辐射源雷达对直升机、通航飞机及无人机等多种目标的微动特征进行了提取与分析。还有学者研究了外辐射源雷达获取目标多维特征的方法,实现了目标的分类识别[3]。
在利用外辐射源雷达进行目标探测定位时,首先对参考通道接收到的直达波信号和监测通道接收到的目标反射信号进行处理,从中估计出包含目标位置信息的定位参数,如到达时间、到达时间差、到达角度、到达频差等。然后再利用包含目标位置信息的定位参数与收发站位置之间的几何关系建立定位方程并求解[5-10]。一般而言,只需其中一个参数便可进行定位。例如,Zhao等[5]和Li等[6]分别基于到达时间和到达时间差进行定位。为了进一步获得更高的定位精度,往往需要联合多个参数进行定位,Pine等[7]基于信号到达不同接收站的时延差和频率差进行定位,Zhao等[8]则基于到达角度、多普勒频率和多普勒频率变化率提出了一种运动目标定位方法。
然而,无论是使用单个参数还是多个参数,外辐射源雷达目标定位性能都会极大地受到发射站位置信息精度的影响。其中,接收站位置可控,故其位置信息容易获得,而发射站由于为不可控的第三方发射站,其精确位置信息有时候往往无法预先获取,极大影响了外辐射源雷达的实际应用。同时,即使可预先获取部分发射站位置信息,实际中也可能会有发射站位置变化或者新增发射站。因此,快速高效的获得发射站位置是外辐射源雷达实用化所必须解决的一个重要问题。
目前,关于外辐射源雷达的发射站定位方法主要是首先估计出合作目标的速度、双基地距离差等中间参数,然后利用合作目标所携带的全球定位系统或广播式自动相关监视(automatic dependent surveillance-broadcast, ADS-B)系统来获取目标精确位置信息,实现对发射站位置的估计。该方法中目标参数估计和位置估计是分开的,故常称为两步定位法。Yi等[11]在获取飞机所携带ADS-B提供的目标位置信息基础上,通过测量目标双基距离与基线距离之差得到多个发射站可能位置的椭圆,多个椭圆交点即为发射站真实位置。Malanowski等[12]也利用ADS-B得到飞行目标的笛卡尔坐标系轨迹信息,并将其变换到双基地轨迹,然后通过匹配双基地轨迹的双站距离和速度得到发射站位置。Krueckemeier等[13]针对多目标情况下关联的复杂性,将三坐标目标信息近似处理转换为两坐标,建立距离和多普勒的代价函数,将双站雷达目标观测值与真实信息正确稳定关联,从而实现发射站定位。
以上研究都是基于两步定位法开展的,该方法在经过中间参数估计后会存在信息损失问题。针对这一不足,本文提出了利用直接定位方法进行发射站定位。直接定位方法最初由Weiss[14]和Amar等[15]提出。该方法直接对原始采样信号进行处理,利用信号中蕴含的目标位置信息,构建与目标位置相关的代价函数,通过优化算法实现定位。直接定位法无需估计中间参数,故信息利用高,损失较少,可获得更好性能,尤其是在低信噪比时优于两步定位法[16-18],因此逐渐成为定位领域的研究热点[19-22]。
Tirer等[23]和Wu等[24]研究了窄带信号源的直接定位,然而外辐射源雷达系统常用的信号为宽带信号,因此并不适用。Ma等[25]研究了宽带信号源的直接定位法,但是需要多个接收站联合进行定位。Weiss[26]研究了接收站和宽带信号源之间存在相对运动时的直接定位法,可用于单个接收站场景,但是其所用的信号源受到一定的约束。Ma等[27]所提算法虽然代价函数不受信号形式的限制,但是未知的发射信号会带来性能下降问题。除此之外,针对正交频分复用(orthogonal frequency division multiplexing, OFDM)信号、非圆信号等特殊信号,也有学者展开相关研究。然而这些研究均是基于OFDM信号的特点,因此适用范围往往受到限制[28-29]。
本文在基于合作式无人机的发射站两步定位方法[12]基础上,提出了一种发射站直接定位法。该方法利用了外辐射源雷达同时接收直达波和目标回波的特性,将航迹信息已知的合作式无人机作为探测目标,并利用接收到的发射站直达波信号代替发射信号,减少了发射信号未知带来的性能下降问题。另外,还分析了该场景下的克拉美罗下界(Cramer-Rao lower bound, CRLB),并将其作为衡量算法性能的参考标准。仿真结果表明,该方法不仅优于两步定位法,且优于文献[27]中信号未知时的直接定位方法。
1 信号模型
考虑如下外辐射源雷达工作场景:一个静止的发射站(位置坐标为u=[x(t),y(t)]T)发射未知宽带信号,静止接收站(位置坐标为q=[x(r),y(r)]T)可通过监测通道和参考通道分别接收来自目标的反射信号和来自发射站的直达波信号,接收站对反射信号进行了K次观测。若观测间隙较短,每个观测间隙内目标的位置和速度可以认为是固定的。设第k个观测间隙目标的位置为pk=p+(k-1)Tv。其中,p为目标初始位置,v为目标运动速度,T为每个观测时隙的时间长度。则目标回波信号经过下变频后,可表示为
rk(t)=αks(t-τk)ej2πfkt+nk(t), 0≤t≤T
(1)
式中:s(t)是发射信号;αk是第k个观测间隙的信道复响应;nk(t)是零均值的复高斯白噪声。设τk≪T,式(1)中时延τk和多普勒频率fk为
(2)
(3)
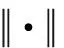
式(1)表示的是一个发射信号未知时的直接定位问题,而当发射信号已知时,其定位性能远高于发射信号未知时的情形[27]。由于发射信号可以通过参考通道获取,因此用来自参考通道的直达波信号代替发射信号,此时式(1)的目标回波信号可改写为
(4)
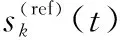
(5)
式(3)中的频移和式(5)中的时延不仅包含发射站位置信息,也包含目标的位置和速度信息,因此将已知位置和速度信息的合作式无人机作为探测目标,则目标回波信号中只包含信道响应和发射站位置两个未知参数。
对每个观测间隙内接收到的目标回波进行N次快拍采样,采样间隔为Ts,则第n个采样时刻的回波信号可以表示为如下形式:
(6)
其中,
(7)
将接收的目标回波信号、直达波信号和采样脉冲分别定义为如下向量:
(8)
那么式(6)的向量形式为
rk=αkFkAksk+nk
(9)
式中:Fk是移位矩阵;Fksk表示将sk位移τk/Ts。发射站定位问题即是从已知的目标回波信号和直达波信号中估计出发射站位置。
2 直接定位法
根据式(9)所示的信号模型,噪声nk服从高斯分布,此时极大似然估计等价于最小二乘估计,因此发射站的位置可以通过最小化如下代价函数得到:
(10)
(11)
将式(11)代入式(10)中可得
(12)
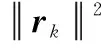
(13)
其中
(14)
(15)
由此得到发射站位置估计值为
(16)
基于上述对方法原理的推导分析,本文所提直接定位方法的主要步骤可总结如下。
步骤1在目标信号源可能存在区域内合理划分网格节点:u1,u2,…,ug,…,uG。
步骤2令g=1,根据式(3)、式(5)和式(8)分别计算网格ug在每个观测间隙内到各观测站的时延矩阵Fk(ug)和多普勒频移矩阵Ak(ug)。
步骤3根据式(14)和式(15)计算每个观测间隙内包含时延和多普勒频移的位置信息矩阵Qk(ug)。
步骤4根据式(13)求得代价函数值L1(ug)。
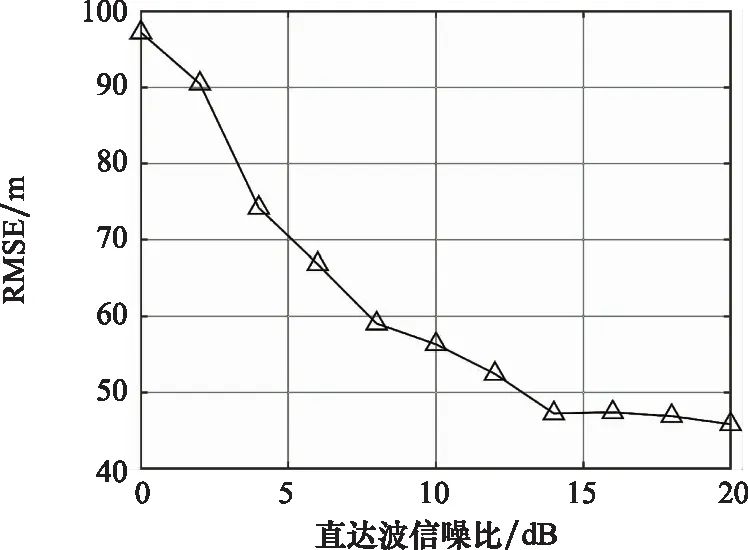
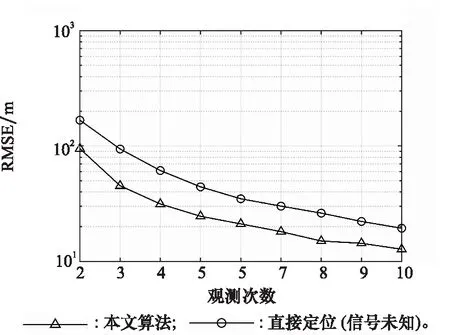
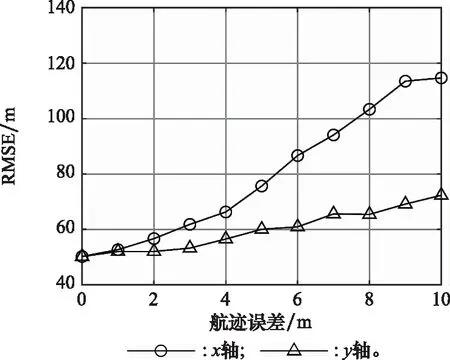
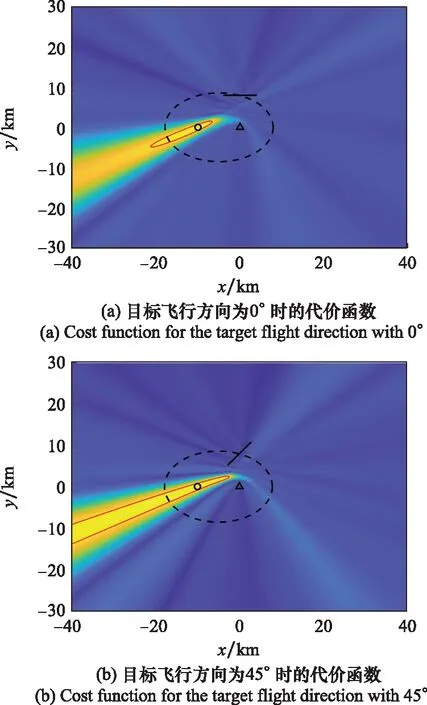
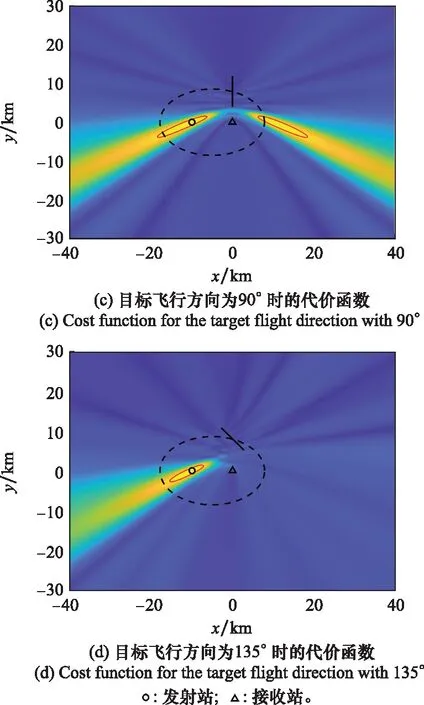
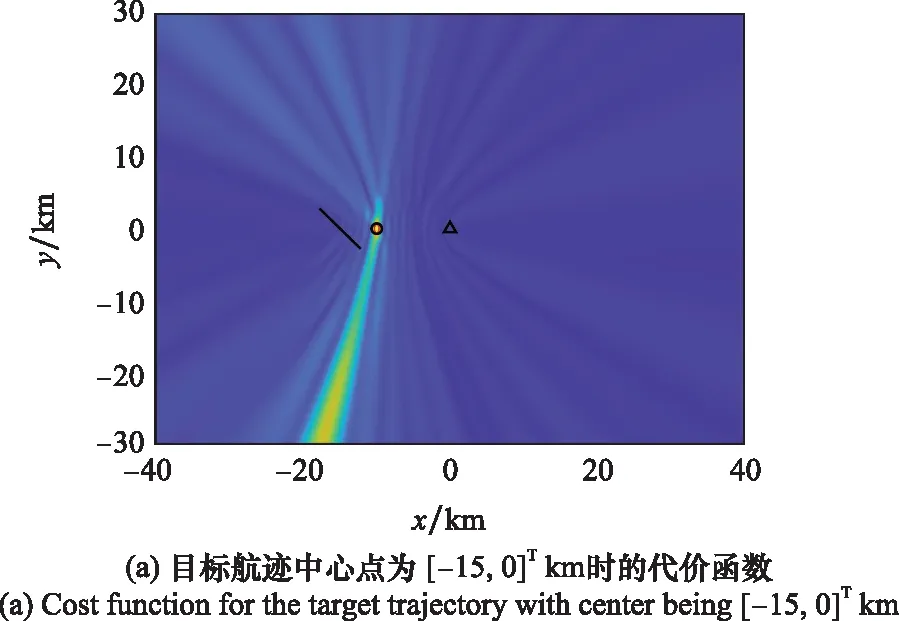
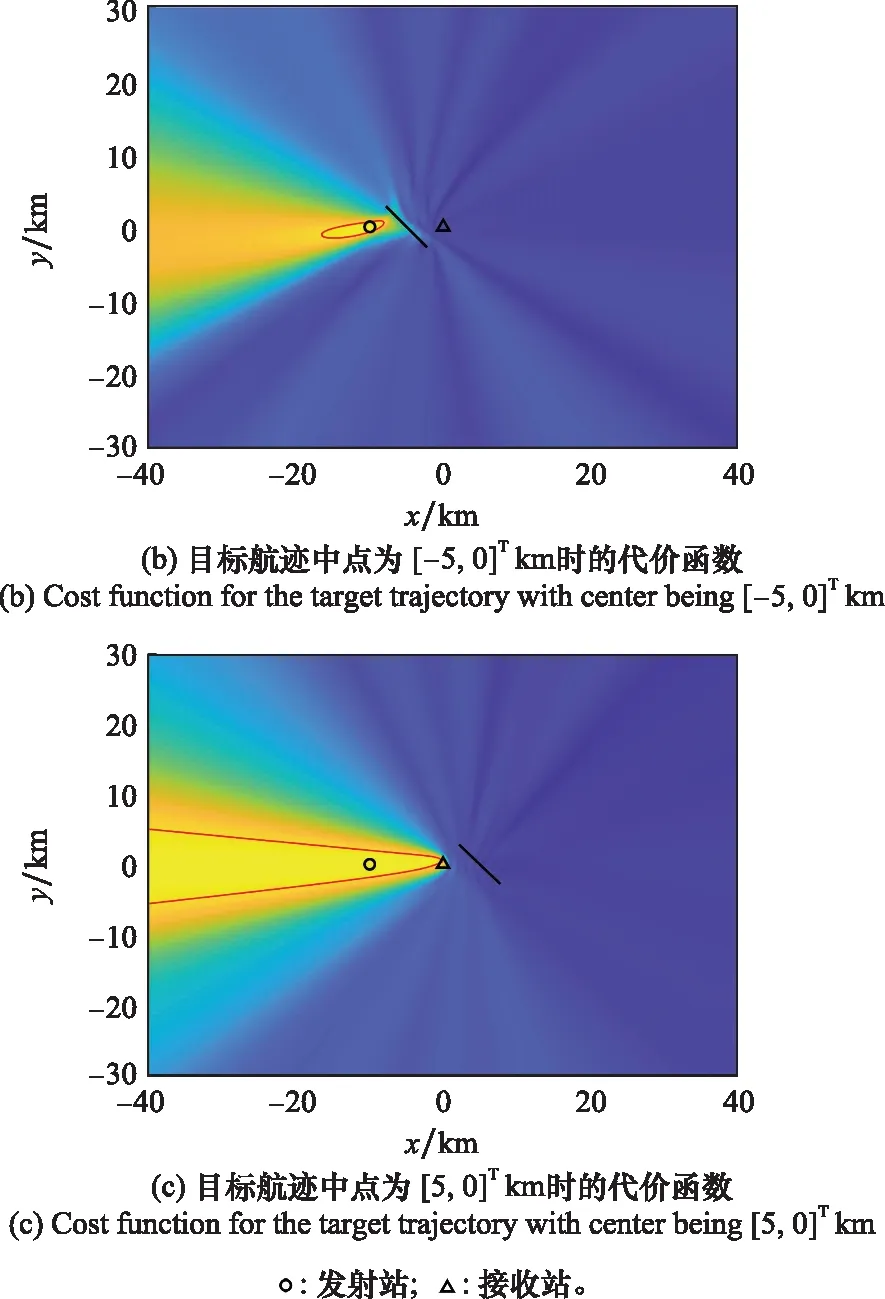
步骤5若g 本节将分析信号发射站位置估计的CRLB。首先根据式(9),可得到接收信号的平均值mk为 mk=αkFkAksk (17) 定义如下向量: (18) (19) 确定完整的Fisher信息量: (20) 其中 (21) 发射站位置估计的CRLB[30]可以表示为 (22) 其中Fisher量的元素[31]可表示为 (23) (24) (25) 其中, (26) (27) (28) (29) (30) 则 (31) (32) (33) (34) 则 (35) (36) 最后,将式(24)、式(25)、式(35)、式(36)代入式(23)可以得到Fisher量的元素,最后再代入分块矩阵式(20)即可求得完整的Fisher信息量,由此可得出发射站位置估计的CRLB。 为了验证所提出算法的定位性能,下面进行仿真分析。仿真设置如下:发射站位置固定为u=[-10,0]Tkm,向外发射载频为762 MHz的地面数字多媒体广播(digital terrestrial multimedia broadcast, DTMB)信号,信号带宽为8 MHz。接收站位置固定为q=[0,0]Tkm,无人机的初始位置为p=[-4,8]Tkm,以飞行速度20 m/s向x轴正方向飞行。接收站对无人机共进行了9次观测,每次观测间隔内无人机飞行距离为1 km。采用蒙特卡罗实验的方法将本文所提算法与文献[27]中信号未知时的直接定位算法及文献[12]中基于合作式无人机的两步法进行对比,并用均方根误差(root mean square error, RMSE)衡量算法性能。RMSE定义如下: (37) 式中:N是蒙特卡罗实验次数,N=1 000;ui是第i次独立实验中发射站位置估计值。 首先,研究在不同无人机回波信号信噪比下,各种不同定位算法的定位精度。假设直达波信号信噪比为20 dB,无人机回波信号信噪比为0 dB到20 dB,其仿真结果如图1所示。从图1可以看出,随着无人机回波信号的信噪比增加,所有算法定位精度都随之提高,但本文所提算法定位精度优于信号未知时的直接定位算法及信号已知时的两步定位法,其性能接近信号已知时定位精度的克拉美罗界。同时也可看出,若发射信号已知,则对于定位性能较信号未知时会有较大的提升。 图1 不同定位算法精度比较Fig.1 Accuracy comparison of different localization algorithms 一般而言,外辐射源雷达所获取的直达波信号并非纯净的,而是会包含噪声信号。为了研究直达波信号噪声对本文算法的影响,假设无人机反射回波信号的信噪比固定为10 dB,直达波信号信噪比为0 dB到20 dB,此时本文算法性能如图2所示。由图2可见,随着直达波信号信噪比的提升,算法性能也会随之提升。 图2 所提算法的RMSE随直达波信号信噪比变化曲线Fig.2 Variation curve of RMSE with the signal to noise ratio of the direct wave signal for the proposed algorithm 其次,研究定位性能与观测次数的关系。在直达波信噪比为20 dB,无人机回波信噪比为20 dB时,观测次数为2~10次之间的定位结果如图3所示。由图3可见,随观测次数增加,两种算法定位精度都随之增加,本文算法相对信号未知时的直接定位算法性能更优。 图3 两种算法的RMSE与观测次数的关系Fig.3 RMSE of two algorithms under different interception intervals 无人机的航迹信息可由GPS获得,但是这些信息往往会存在误差,因此本文将研究这些误差对算法性能的影响。仿真参数设置如下:仿真设置如下,发射站位置为u=[-10,0]Tkm,接收站位置为q=[0,0]Tkm,无人机的初始位置为p=[-4,8]Tkm,以飞行速度20 m/s向x轴正方向飞行。接收站对无人机共进行了9次观测,每次观测间隔内无人机飞行距离为1 km,目标回波信号与发射站直达波信号信噪比均为10 dB。假设获得的无人机航迹与实际的无人机航迹在x轴或y轴方向存在一定的偏差,则图4展示了存在误差时算法的性能。由图4可知,随着航迹误差的增大,本文算法性能也随之下降。 图4 所提算法的RMSE随无人机位置误差变化曲线Fig.4 Variation curve of RMSE with unmanned aerial vehicle position error for the proposed algorithm 然后,进一步研究不同无人机飞行方向对代价函数的影响。假设无人机的航迹与x轴正方向所形成的夹角即为无人机的飞行方向,无人机分别沿着0°、45°、90°、135° 这4个方向以速度20 m/s飞行,4条航迹长度固定为8 km且航迹中心点均为p=[0,8]Tkm,接收站对无人机共进行了9次观测,每次观测无人机移动1 km。代价函数仿真结果如图5所示。其中,黑色圆形和三角形分别表示发射站和接收站,黑色虚线表示无人机处于航迹中心点时的双基距离,黑色实线和红色实线分别表示无人机航迹和代价函数等高线。 图5 不同飞行方向时的代价函数Fig.5 Cost function for different flight directions 由图5可知,无人机飞行角度为135°时,红色等高线包围的区域最小,则定位性能最高。而当无人机飞行角度为90°时,会出现定位模糊。 最后,研究无人机相对于发射站和接收站的飞行位置对代价函数的影响。假设无人机飞行角度为135°,分别按照3条不同的航迹以速度大小为20 m/s飞行,3条航迹长度固定为8 km且航迹中心点分别为[-15,0]Tkm、 [-5,0]Tkm和[5,0]Tkm,其他条件不变。代价函数的仿真结果如图6所示。从图6可见,无人机在背离接收站的位置飞行时,定位性能最好。 图6 不同相对飞行位置时的代价函数Fig.6 Cost function for different relative flight positions 本文针对外辐射源雷达系统中发射站快速定位问题,提出了以无人机作为合作目标,采用直接定位对发射站进行定位信息获取的方法。并针对常规直接定位方法在信号形式未知带来的性能下降问题,将直达波信号作为已知发射信号,不仅可以得到较常规直接定位方法和两步定位法相对更好的性能,而且其定位精度逼近CRLB。当接收信号信噪比和观测次数增加,其定位精度也随之增加。同时,合作目标相对于收发站位的飞行方向和位置对定位性能也有不同影响,这对于实际应用具有较好的参考意义。仿真结果验证了所提方法的优越性。
3 定位方法性能分析

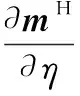

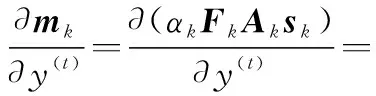
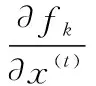
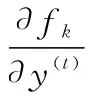
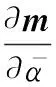
4 仿真实验与分析
4.1 仿真1:不同定位算法性能比较

4.2 仿真2:信号参数对算法性能影响
4.3 仿真3:无人机航迹对算法性能影响
5 结 论
