复合地层中盾构滚刀磨损实用预测方法及应用
2023-01-31龚泽佳鱼志鸿章定文李兆国
龚泽佳,鱼志鸿,章定文,3,冯 硕,李兆国
(1. 东南大学交通学院,江苏南京 211189; 2. 中建八局轨道交通建设有限公司,江苏南京 210046; 3. 东南大学道路交通工程国家级实验教学示范中心,江苏南京 211189)
0 引 言
盾构法因具有不影响地面正常活动、对土体扰动小等优点,近年来在地铁隧道施工中被广泛采用。刀具磨损常导致掘进工效降低甚至刀具失效,是盾构施工中面临的主要挑战。目前掘进中的刀具磨损状况主要依靠经验判断,也可采用停机后人工进仓检查的方法,但是危险性很高且代价较大。实际施工过程中一般只有在无法掘进时才进行开仓检查,这时盾构刀具通常已发生了严重的磨损或者变形,无论是换刀难度还是工程进度都会受到严重影响。因此准确预测刀具磨损状况具有重要意义。
国内外学者在滚刀磨损机理、滚刀破岩力学模型和滚刀磨损预测模型等方面进行了大量研究。吴俊等[1-2]基于金属摩擦学理论指出,盾构刀具磨损主要包括磨粒磨损、黏着磨损和疲劳磨损,其中磨粒磨损和黏着磨损是刀具磨损的主因。罗华[3]将磨粒磨损分为两类,其中二体磨粒磨损是磨料沿一个固体表面相对运动产生的高应力碾碎式磨损,三体磨粒磨损是坚硬的矿物颗粒或脱落的金属颗粒夹在刀具和岩石表面之间摩擦时,产生的高接触应力导致的磨损。赵海鸣等[4]指出以磨粒磨损为主要形式的滚刀磨损中,引起刀圈表面材料损耗的机制主要是基于塑性固体的显微切削与犁沟去除,以及基于韧性固体的微观断裂剥离。Su等[5]依托深圳地铁6号线盾构工程分析了刀盘不同位置滚刀的磨损类型,统计结果显示磨粒磨损为滚刀磨损的主要原因,并与相对滑动距离和贯入度直接相关。
磨损是两个固体接触表面之间相互作用的结果。关于滚刀与岩石的相互作用和运动模式,国内外学者基于不同的接触理论和摩擦理论对滚刀破岩的过程进行了定量描述,得出了很多经典的滚刀力学模型。Evans等[6]认为滚刀破岩所需的垂直力和刀圈与岩石接触表面的投影面积成正比,其比值为岩石的单轴抗压强度。Tosaburo[7]采用了Evans垂直力计算公式,并分别基于挤压破碎理论和剪切破碎理论提出了两种侧向力计算公式。Roxborough等[8]修正了Evans的理论,认为公式中的接触面投影面积应为矩形。Sanio[9]基于几何分析和室内滚刀切削试验,提出了一个较实用的滚刀受力计算模型——科罗拉多矿业学院模型(CSM模型),该模型经过了大量室内试验和实际工程的验证[10-13],相比于其他模型具有更高的准确性。
滚刀磨损预测模型的构建主要通过掘进参数的统计分析或滚刀破岩规律的理论推导来实现。挪威科技大学构建的NTNU模型[14]采用统计方法,基于大量工程的现场掘进数据和岩层地质参数得到经验公式以预测磨损;石超等[15]基于BP神经网络建立了滚刀磨损预测模型,并采用遗传算法和粒子群算法提升模型精度;祝和意等[16]建立了基于磨粒磨损的滚刀磨损速率预测模型,并结合实测数据对预测结果进行了误差分析;李彬嘉等[17]基于CSM力学模型模拟了滚刀动态受力特性,并通过与现场实测值对比验证其准确性。
本文依托深圳地铁13号线白应区间盾构隧道工程,研究基于磨粒磨损的盘形滚刀磨损预测模型,在CSM力学模型的基础上推导出更为实用的滚刀磨损量预测方法,并通过案例实测数据证明该方法预测滚刀磨损的可行性。
1 深圳13号线白应区间工程概况
1.1 工程地质条件
深圳地铁13号线白应区间盾构隧道全长2.25 km,左右线间距为11.8~25.0 m,隧道埋深8.6~49.2 m。区间普遍分布有风化花岗岩夹层,地层软硬分布不均匀且变化频率高,部分区间存在基岩突起现象并伴有孤石发育,工程地质条件较为复杂。图1为区间穿越岩层的分布比例。
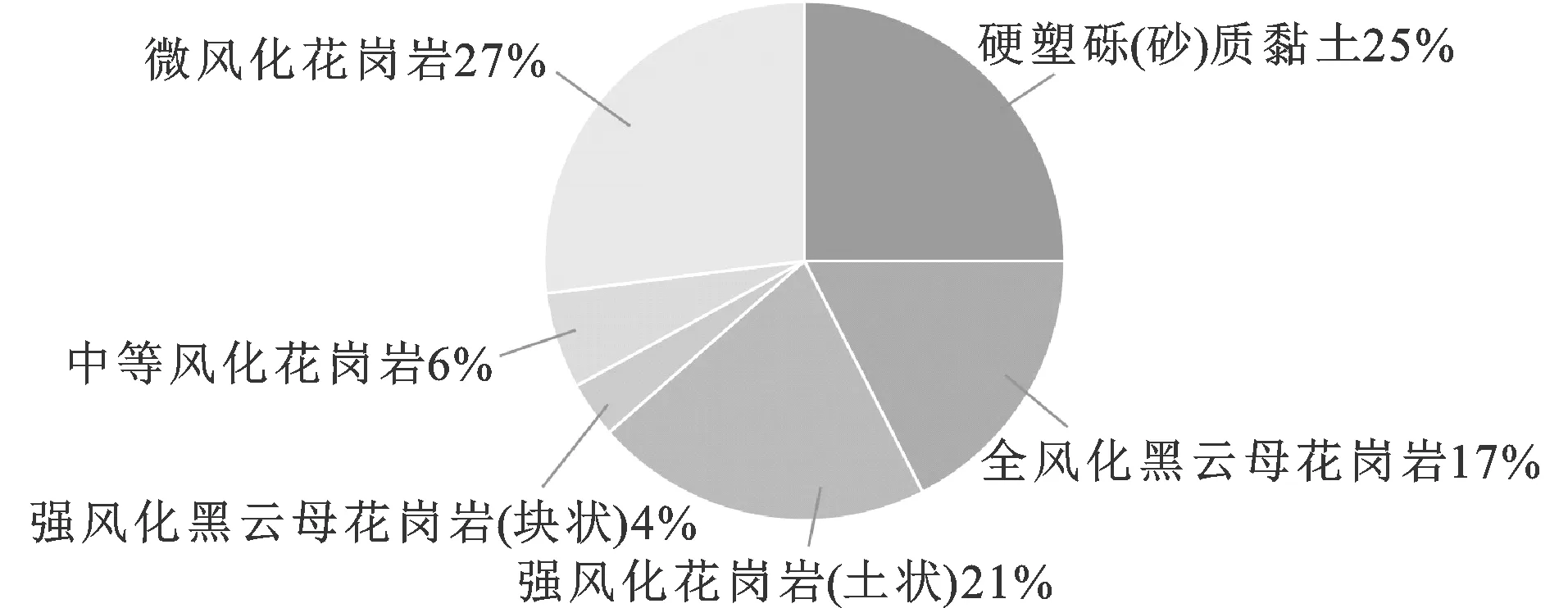
1.2 刀盘刀具配置
白应区间采用2台EPB/TBM双模式盾构机,可在土压模式(半敞开&闭胸)和TBM模式下互相切换。为平衡盾构机在不同地质条件下的掘进工效与可靠度,刀盘采用辐板式复合结构设计,拥有较宽的辐条和小块的面板,并可根据掘进地层情况进行改造。
表1为刀盘配置情况。由于盾构区间穿越的地层数量较多、地质条件复杂且小部分区间为全断面硬岩地层,盾构刀盘选择了开口率较低、中心双联滚刀的配置,便于在适应多变地质环境的同时保持较高的破岩效率。
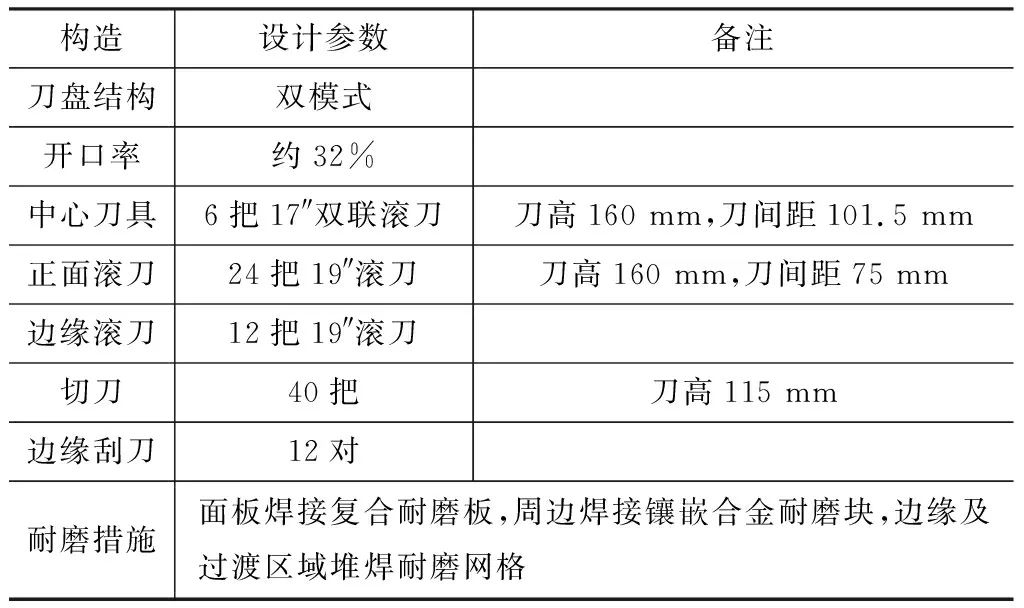
表1 刀盘设计参数Table 1 Cutter head design parameters
1.3 滚刀磨损与换刀数据统计
依据刀具破岩机制和磨损机理,滚刀磨损失效方式主要包括均匀磨损和非均匀磨损。均匀磨损常见于岩层均一、强度较高的地层情况;非均匀磨损主要发生于松散地层或黏性土地层中,通常为刀盘结泥饼导致滚刀停转形成偏磨。本节统计了深圳地铁13号线白应区间滚刀磨损情况,从而得到该区间滚刀的主要失效方式。
深圳地铁13号线白应区间左线掘进1~600环共计开仓换刀13次,其中带压换刀12次,常压换刀1次;右线掘进1~500环共计开仓换刀26次,其中带压换刀15次,常压换刀11次。左线90~140环通过孤石分布区域,同一掘进面内软硬差距悬殊,增加了滚刀崩刃的风险。右线160~260环掘进通过全断面硬岩段,区间微风化黑云母花岗岩硬度可达90 MPa,高硬度高磨蚀性岩体增加了开仓换刀的频率。左右线换刀统计见表2。

表2 左右线换刀统计Table 2 Statistics of tool change of left and right lines
由表2可知,均匀磨损是滚刀失效的主要形式。均匀磨损主要集中于正面滚刀和边缘滚刀,中心双联滚刀绝大多数由于结泥饼导致了偏磨。右线由于岩石整体硬度较大,滚刀崩刃、掉刀和偏磨等破坏情况的比例均高于左线。基于上述分析,可将均匀磨损的滚刀失效方式作为磨损预测的主要对象,且应排除中心滚刀磨损对预测模型的影响。
2 滚刀磨损实用预测方法
滚刀磨损机理主要包括磨粒磨损、黏着磨损和疲劳磨损,三者并非单独出现,而是互相耦合与影响。考虑到磨粒磨损机理对滚刀以均匀磨损为主的失效方式描述效果更好,本方法引入Rabinowicz[18]磨粒磨损计算公式并构建了适用于深圳地区岩性的磨损实用预测方法。
2.1 Rabinowicz滚刀磨粒磨损计算模型
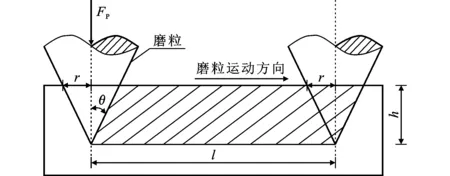
滚刀均匀磨损失效的主要原因为磨粒磨损,即硬质颗粒在滚刀和岩石之前滑动造成的切削和犁沟效应。Rabinowicz提出的磨粒磨损计算模型是以二体磨粒磨损的切削作用为主的定量计算公式,模型如图2所示[18-19]。
模型中有效半径为r、中心角度为2θ的微圆锥形磨粒受法向荷载FP作用,在受压屈服强度为σs的被磨物体表面滑动,滑动距离为l,切削深度为h。假设共有n个锥形磨粒且磨粒与被磨物体的接触概率为P,即可得n个锥形体滑动距离l产生的磨粒磨损体积Vn为
(1)
式中:K=Pcot(θ)为磨粒磨损系数,主要与磨粒材料、尺寸、形状等参数有关,依据参考值取K=8×10-3;滚刀受压屈服强度σs在掘进过程中基本保持不变,依据合金钢强度规范标准[20]取σs=1 636 MPa。
式(1)表明,在磨粒磨损系数和刀具屈服强度保持不变的条件下,磨损体积与接触面法向荷载和滑 动距离成正比。依据滚刀CSM模型可得接触面法向荷载Fp,依据滑移率定义式可得滑动距离l,将二者代入式(1)并结合岩石强度指标和盾构掘进参数即可求解滚刀磨粒磨损体积。
2.2 滚刀滑动距离确定
根据图3[21-22]中的几何关系可得接岩角度φ=arccos(R-p/R),在盘形滚刀制式确定的情况下[以正面滚刀使用标准19 in(直径为483 mm)制式为标准],可进一步通过非线性拟合得到角度φ和滚刀贯入深度p的近似关系式,即
φ≈0.009p0.5
(2)
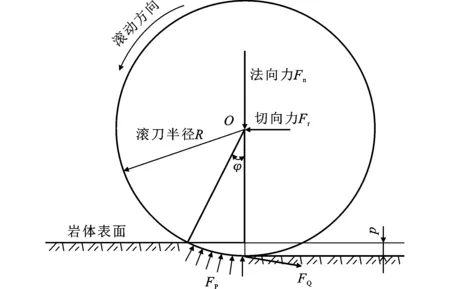
盾构机在岩石中掘进时,贯入深度一般不超过20 mm。滚刀刀圈材料刚度大,可以看作是一个弹性圆柱;岩石也可以看作是弹性体。岩石平面可视为具有无限半径的圆柱体。因此根据赫兹弹性接触理论,圆盘刀具与岩石之间的接触区域为椭圆形。由于接触材料力学性能的差异和切向合力FQ的影响,接触部分同时包含滚动区和滑移区。滚动和滑动两种运动的叠加导致滚刀外缘的实际运动距离小于滚刀破岩的推进总距离,两种距离之差就是滑动距离。由于滚刀外缘实际运动距离无法直接求出,滑动距离可单由滚刀推进总距离表示为
l=ξL
(3)
式中:ξ为滚刀滑移率;L为滚刀推进总距离。
滚刀推进总距离L可通过将盾构掘进参数代入式(4)求得。
(4)
式中:Ri为第i个滚刀在刀盘中的安装半径;Ln为掘进距离;v为掘进速度;rn为刀盘转速。
滑移率ξ由Popov[23]从接触力学角度定义为
(5)
式中:α=Rφ/2,物理意义为椭圆形接触面的长半轴;μ为硬岩摩擦因数。
定义接触面切向力与法向力之比FQ/FP为切削系数C,将式(2)代入α=Rφ/2,则式(5)可简化为
(6)
实际计算中,切削系数C通常由掘进参数计算得出,即
(7)
式中:MT为刀盘的总扭矩;FT为刀盘的总推力;N为滚刀的数量。
从式(6)中可看出,在滚刀半径R确定的条件下,滚刀滑移率ξ与贯入深度p、硬岩摩擦因数μ和切削系数C有关。由统计数据可知,C大于0.05,且最大值约为3μ/4。而摩擦因数μ通常在0.25~0.75之间变化,由此可得C的变化范围为0.05~0.6。为减少未知变量,现分析贯入深度p和摩擦因数μ对滑移率ξ的影响程度大小。当摩擦因数μ=0.75时,不同贯入深度p下滑移率ξ与切削系数C之间的关系如图4所示。

当贯入深度p=10 mm时,不同摩擦因数μ下的滑移率ξ和切削系数C之间的关系如图5所示。
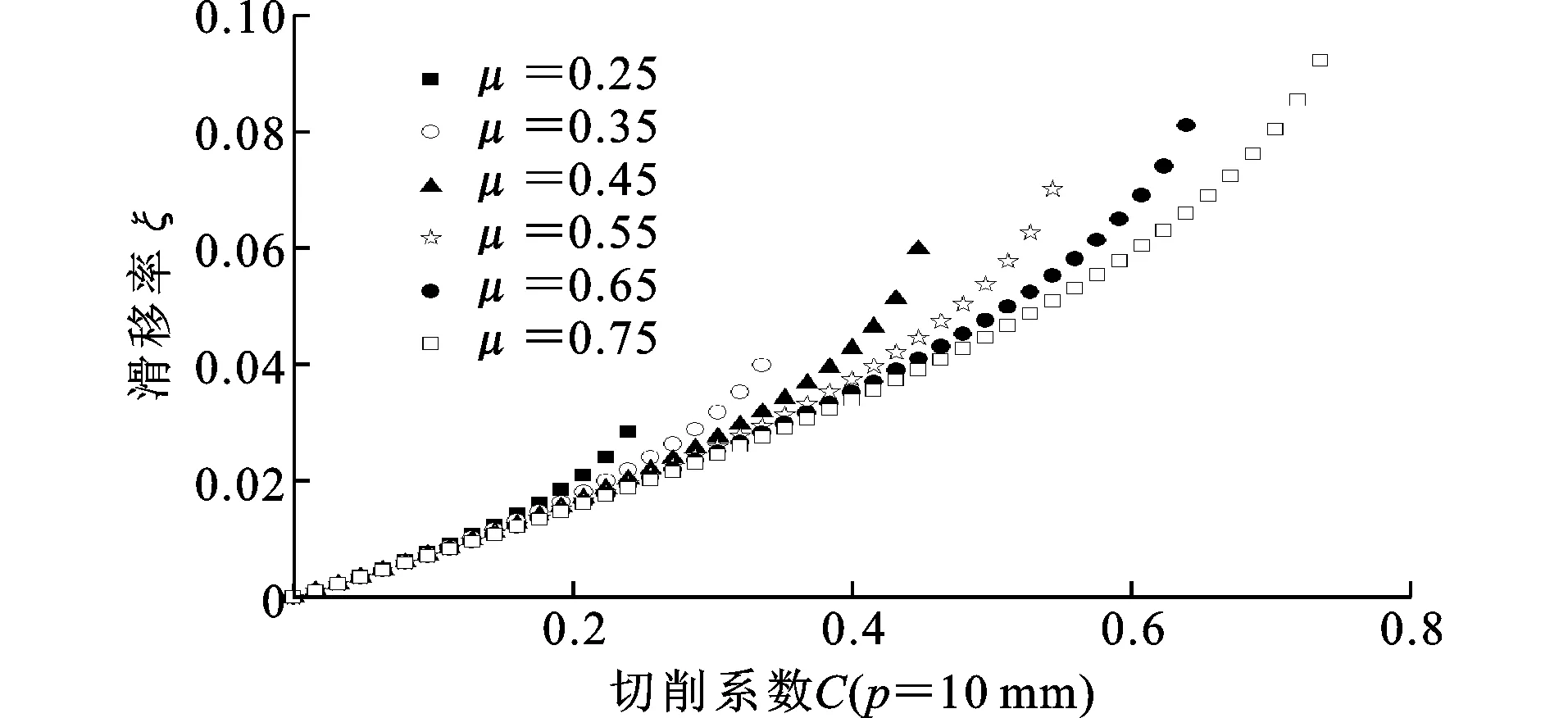
对比图4、5可知,μ值变化对ξ与C关系的影响较小。根据盾构机设计资料,钢-土间摩擦因数宜取0.25;钢-岩石间摩擦因数视情况而定。岩石干燥、水湿润、泥浆湿润3个状态下花岗岩的摩擦因数分别为0.47~0.55、0.46~0.53、0.45~0.52,可取摩擦因数μ=0.5。将μ=0.5代入式(6)后滑移率ξ的计算公式可简化为
(8)
将式(4)、(8)代入式(3)并结合滚刀贯入深度计算公式p=v/rn,可得滑动距离l的计算公式为
(9)
2.3 接触面法向荷载确定
接触面法向荷载FP可由接触面合力F间接求得,计算公式为
FP=Fcos(φ/2)
(10)
基于CSM模型可推导出滚刀岩石接触面合力计算公式,即
(11)
式中:量纲一的系数C通过试验确定取值为2.12;d为滚刀刃宽;Ψ为压力分布系数,随刀尖宽度增加而减小,通常取Ψ=-0.2~0.2,本文取0.1;S为滚刀间距;σc、σt分别为岩石的抗压强度、抗拉强度。
由于滚刀配置保持不变,可取19 in滚刀刃宽(d=20 mm)及半径(R=241.5 mm)、正面滚刀间距S=75 mm作为定值。将式(2)和其他定值代入式(11),可得到仅关于贯入深度p、岩石抗压强度σc、抗拉强度σt的接触面合力公式,即
(12)
将式(2)、(12)代入式(10),即可得接触面法向荷载FP计算公式,即
(13)
2.4 滚刀磨损量实用计算公式
把式(9)、(13)代入式(1),可得基于磨粒磨损的滚刀磨损量计算公式为
(14)
(15)
式中:常数项α=4.219 7×10-4;τ为修正系数,可由实测磨损体积与未修正磨损体积的倍数关系得到;β(p)为关于贯入深度p的函数。
综上所述,在滚刀制式和材料性能保持不变的条件下,已知滚刀安装半径Ri、掘进距离Ln、岩体力学参数σc和σt和盾构机主要掘进参数(掘进速度、刀盘转速、刀盘扭矩和刀盘推力),即可由式(14)求得单个滚刀在某段掘进过程中的磨损体积Vn。
为更方便与实测数据比对,可通过几何关系得到滚刀磨损高度表达式,即
(16)
式中:δn为滚刀磨损高度。
3 工程案例应用与分析
选取深圳地铁13号线左线561~595环进行滚刀磨耗预测分析。该盾构段先后掘进通过了强风化黑云母花岗岩(土状)、强风化黑云母花岗岩(块状)和中风化黑云母花岗岩三地层的界面(565~580环),属典型软硬不均复合地层结构;直接掘进通过了大直径孤石段(568~575环);通过的中风化黑云母花岗岩层(581~589环)和微风化黑云母花岗岩层(590~595环)属高硬度高磨蚀性岩层界面,易发生偏磨、崩刃等问题。
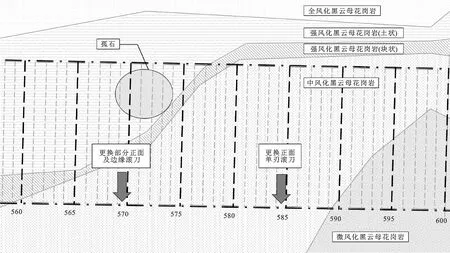
左线561~595环地层变化频繁,单环掘进周期长,期间有2次换刀记录(570环,更换S13~S36正面滚刀和全部边缘刮刀;585环,更换S13~S36正面滚刀),选择2次开仓均被更换过的滚刀即可精确测量更换期间的磨损量,适合作为分析案例。盾构段地层纵断面如图6所示。
3.1 单个正面滚刀磨耗预测与分析
现选择S29号和S35号正面滚刀作为磨损预测对象,这两把刀具均于570环处更换为全新国产光面滚刀,又均于585环处达到均匀磨损失效标准被换下。571~585环区间为非均质地层,571~575环区间存在孤石和上软下硬不良地质条件。参考详勘报告,同一掘进面内含不同地层的情况取单轴抗压强度的平均值,花岗岩抗拉强度一般为抗压强度的1/10左右[24],由此得到岩石抗压强度σc、抗拉强度σt如表3所示。
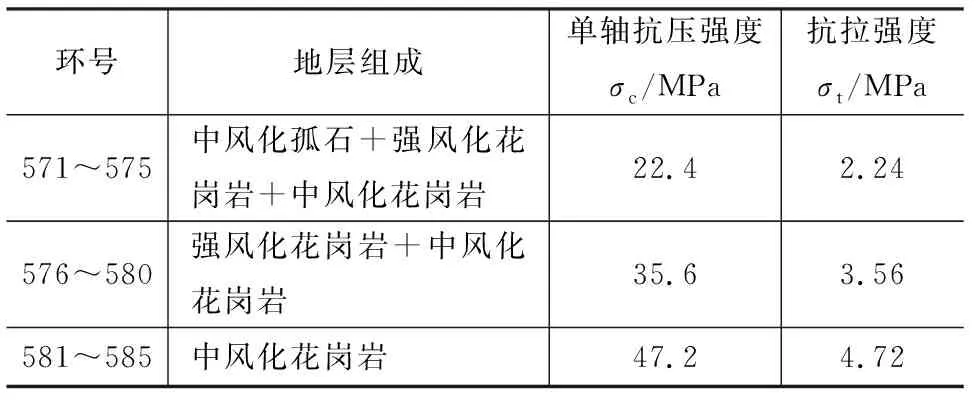
表3 571~585环岩石强度参数Table 3 Rock strength parameters of ring 571-585
两把滚刀的安装半径分别为RS29=2 519 mm、RS35=2 969 mm;单环掘进距离Ln=1 500 mm,共掘进15环。将盾构机掘进参数和地层力学参数代入滚刀磨损体积预测模型,可得到15环内滚刀S29和S35的平均未修正磨损体积Vni=22 986 mm3。两把滚刀的实测磨损高度均为14 mm,据此可由式(16)反算得滚刀实际磨损体积Vn′=412 554 mm3。为便于预测值和实测值的定量比较,取修正系数τ=Vn′/Vni≈18,代入式(14)、(16)后可绘出修正后的滚刀磨损高度累计值预测曲线,如图7所示。

3.2 局部掘进区间整体磨损量预测与分析
盾构机实时掘进数据通常以1 min为间隔进行不间断监测,因此原始数据中存在大量无效及冗余数据,但通过细致的参数变化可以更好地体现非理想状态下盾构机刀具破岩及磨损情况。本次模拟共处理了左线实时盾构掘进原始数据27 000余条,包含571~595环共计35环、20个工作日的盾构机实时监测数据。经过筛选后,可用于模型构造和分析处理的数据共计5 429条。571~595环岩石强度如表4所示。

表4 571~595环岩石强度参数Table 4 Rock strength parameters of ring 571-595
设VT为所有正面滚刀的整体磨损量,结合式(14)可得整体磨损量计算公式为
(17)
通过式(17)可求得单位时间间隔(1 min)内正面滚刀平均磨损量,以环号为单位均布后可绘制出如图8的折线图。
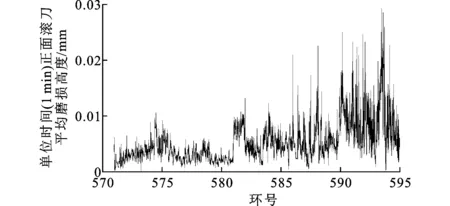
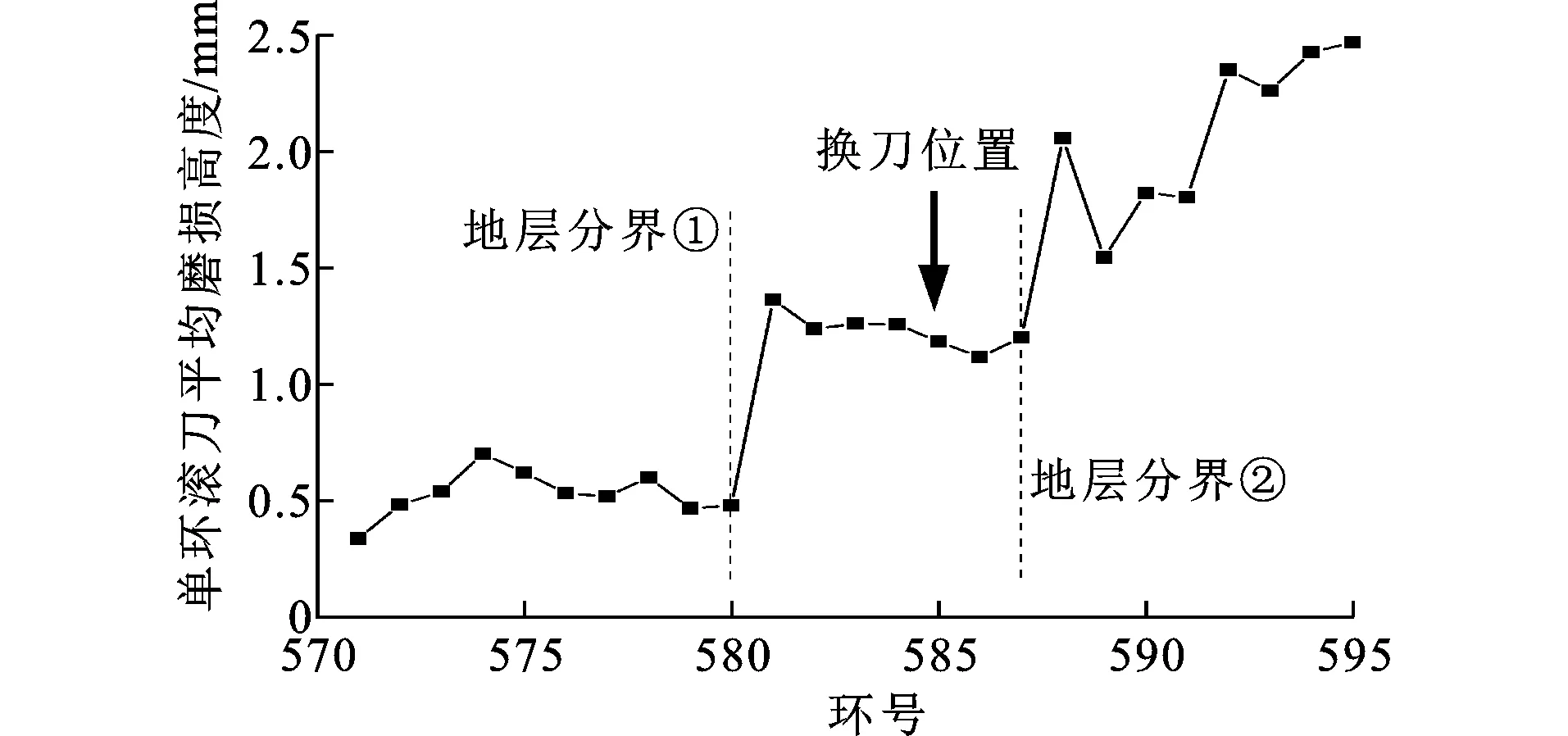
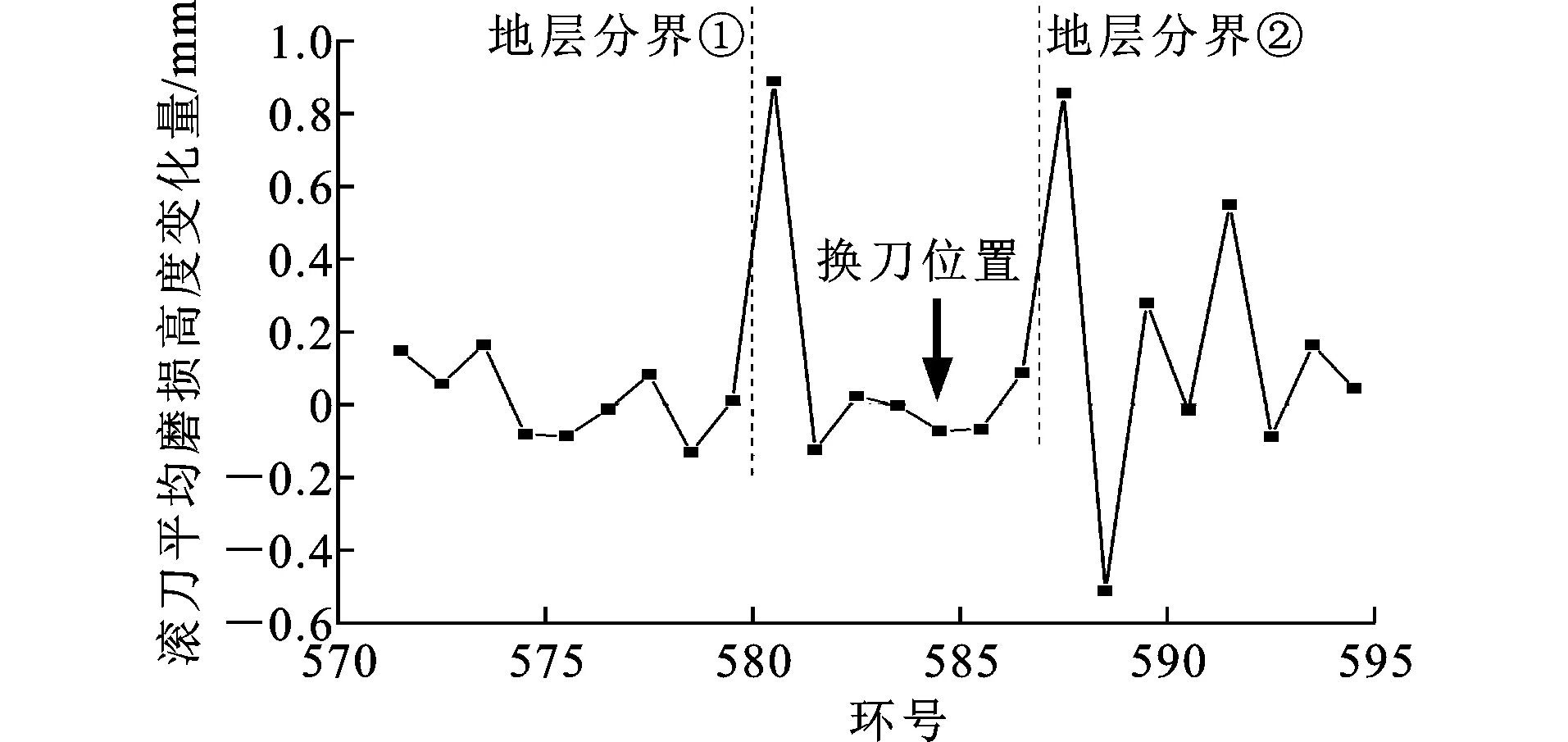
基于图8数据,将单位时间磨损量按时刻所属环号归类并相加,可得到单环滚刀平均磨损高度(图9),计算相邻两环间磨损高度差值,可得滚刀平均磨损高度变化量(图10)。图10中纵轴数值为正即表示磨损量较上一环有所增加;数值为负则相反。磨损高度差值绝对值的大小则代表了磨损量增加或降低的速率。
滚刀的磨粒磨损和其他磨损形式是互相增益和促进的,随着磨损量的增加,滚刀的磨损速率也会加快,而全新滚刀的磨损量和磨损速率则较低。因此可通过滚刀平均单环磨损量和平均磨耗速率大小预测滚刀的磨损状态并确定换刀时机。
根据图9、10与实际刀盘扭矩和推力变化曲线及换刀数据的对比,可对预测的准确性和模型对实际工况的表征效果进行评估和分析。滚刀磨损量变化的外部原因可大致归类为人为因素和地质条件因素,下面将基于这两个因素定性评价模型的表征效果。
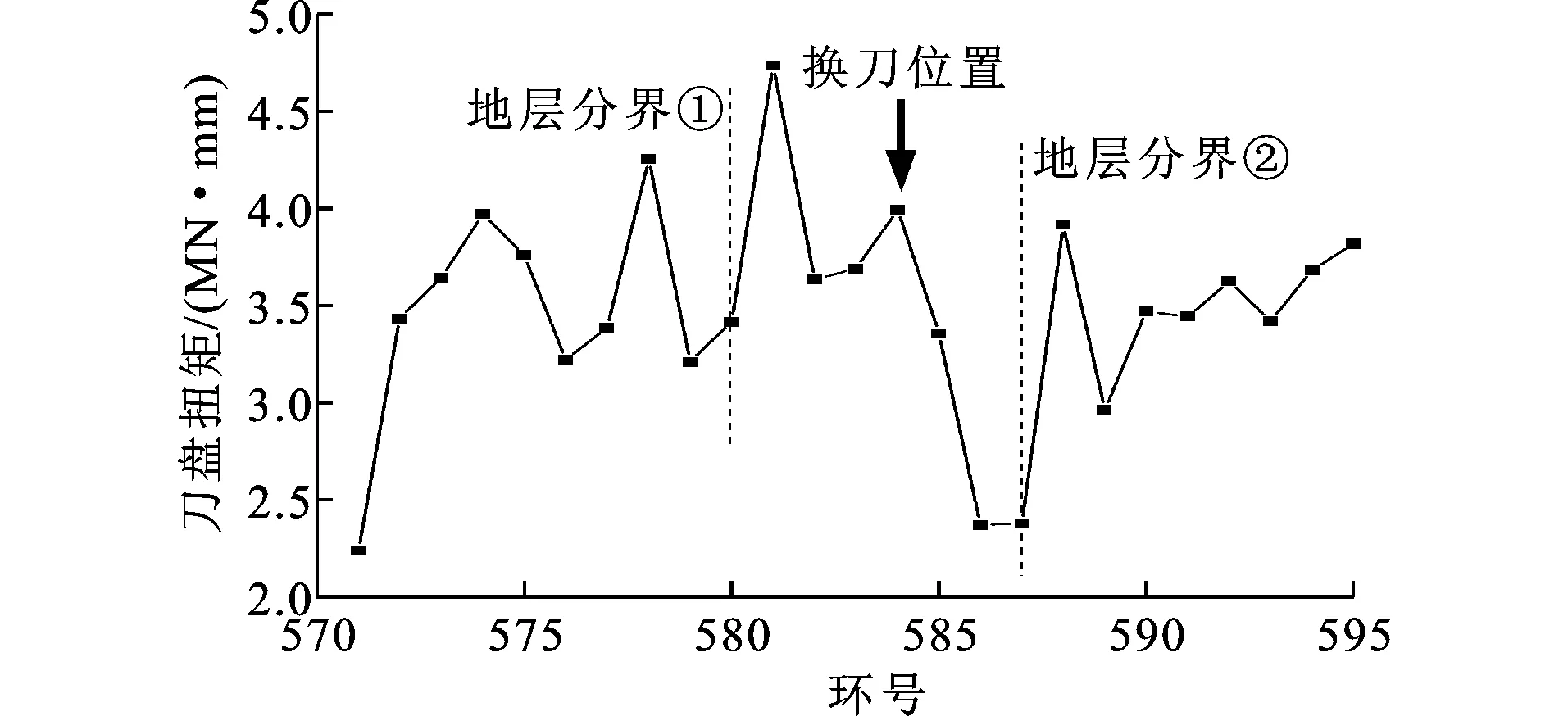
结合图9和图11的单环扭矩平均值变化曲线,可以观察到在585环换刀之后单环刀具磨损量和扭矩有明显下降,这说明本模型有一定预测滚刀磨损程度的能力,并对换刀导致的滚刀磨损量降低表征效果良好,在结合扭矩等其他掘进参数进行分析时可取得更好效果。
结合图9、10和图6的地质纵断面图可以看出,在580环和590环的地层分界面,滚刀磨损量和磨损速率均明显增加,这说明本预测模型能较好地表征地质条件对滚刀磨损的影响,但从图10可以看出,地层分界处的预测结果变化过于突兀,进一步细化岩体力学参数的分组可使数据过渡更为平滑,但需要更精确的勘察结果支持。
4 结语
(1)本文通过对深圳地铁13号线白应区间盾构滚刀磨损数据的总结和研究,确定了以磨粒磨损为主要失效形式的滚刀磨损规律。
(2)依据Rabinowicz滚刀磨粒磨损计算模型提出了一种滚刀磨损预测方法。该方法优化了滑动距离计算流程并应用CSM模型计算了接触面法向荷载,最终得出关于滑动距离、接触面法向荷载、刀具材料强度的滚刀磨损体积计算公式。
(3)应用滚刀磨损预测方法得到了深圳地铁13号线白应区间复合地层段单个正面滚刀的磨损高度累计值变化曲线,结果显示磨损速率随磨损累计值的增加呈上升趋势,预测磨损量经修正后与实测值偏差小于5%,符合均匀磨损条件下滚刀的磨损规律。
(4)拓展上述单个滚刀的磨损预测方法并计算所有正面滚刀的整体磨损量,结合该复合地层段岩层界面和换刀记录进行分析,结果显示整体磨损预测的结果与地层变化趋势较为吻合,在地层分界处磨损量均有50%以上的增加,说明预测方法较为合理,有一定的应用价值。
