多年调节水库调蓄的影响因素判别与影响时长分析

2023-01-31鲍淑君周翔南尚文绣

中国水利水电科学研究院学报 2022年6期

鲍淑君，周翔南，尚文绣，尚弈

（1.国家发展和改革委员会国际合作中心，北京 100045；2.黄河勘测规划设计研究院有限公司，河南郑州 450003；3.华北水利水电大学，河南郑州 450045）

1 研究背景

多年调节水库通过蓄丰补枯，在应对连续枯水、保障供水安全中发挥了重要作用[1-3]。水库调蓄可能受到上游来水、下游用水、入库泥沙、水文预报、管理策略等多因素的复合影响[4-7]，明确多年调节水库调蓄的影响因素及其影响时长，对于科学制定水库调蓄方案、有效应对连续枯水、开展水库调度精准模拟优化、提高水库运行综合效益等具有重要意义。在多年调节水库调蓄的影响因素上，已有研究基于理论和实践经验，人为筛选出水库调蓄的可能影响因素[8-11]，缺少对可能影响因素准确性的判别方法。现有分析方法具有较强的主观性，受研究者个人认知的影响较大；此外，由于各水库的气象水文条件、规模、任务等存在差异，影响因素不尽相同，仅通过理论和经验难以保障提出的可能影响因素的准确性，需要结合水库的长系列实际调蓄过程进一步量化研究。多年调节水库调蓄周期长，前期来水、用水等因素可能持续影响当前及未来的水库调蓄方案，但已有研究缺少影响因素的影响时长量化分析方法。

格兰杰因果关系检验（Granger causality test）是经济学和社会学领域常用的分析方法，用于检验两个时间序列是否存在统计学意义的因果关系[12-14]。格兰杰因果关系检验已经在水资源相关研究中得到了初步应用，例如，雷玉桃等[15]识别了我国工业用水量的影响因素，申建建等[16]建立了水电站调峰压力指标间的联动关系，秦腾等[17]研究了不同地区水资源利用效率间的影响关系。格兰杰因果关系检验为基于历史实测资料识别水库实际调蓄中的影响因素提供了可行方法。此外，格兰杰因果关系检验结果随着前期信息滞后时长的变化而改变，为识别影响因素的作用时长提供了可能。但目前尚无研究将格兰杰因果关系检验应用于多年调节水库调蓄的影响因素判别与影响时长分析中。

本文应用格兰杰因果关系检验判别多年调节水库的影响因素，提出改进方法将格兰杰因果关系检验用于分析各因素的影响时长，结合理论分析、多元线性回归等分析了格兰杰因果关系检验结果的合理性，分析了多年调节水库在黄河供水安全保障中发挥的作用。

2 研究方法简介

2.1 方法步骤多年调节水库调蓄的影响因素判别方法步骤为：（1）基于理论和经验提出可能的影响因素；（2）对可能的影响因素及水库调蓄的时间序列进行平稳性检验；（3）对通过平稳性检验的时间序列进行格兰杰因果关系检验；（4）对通过格兰杰因果关系检验的时间序列进行多元线性回归F检验；（5）当步骤（3）和步骤（4）的检验结果一致时，认为影响因素对多年调节水库调蓄具有显著影响，否则需结合理论和实践经验判断检验结果的合理性。

影响因素的影响时长分析方法步骤为：（1）采用格兰杰因果关系检验得到影响因素的最长显著影响时长；（2）采用多元线性回归t检验得到影响因素在不同时段的影响程度差异。

2.2 平稳性检验具有趋势或周期性变化的时间序列会导致格兰杰因果关系检验失效，因此需要先对数据序列进行平稳性检验[15]。采用增广的迪基-富勒（Augmented Dickey-Fuller，ADF）单位根检验判断时间序列的平稳性。该方法假设待检验序列为非平稳时间序列，如果检验结果为拒绝原假设，则认为序列为平稳时间序列[18]。ADF检验模型有3种形式：不含截距项和趋势项，仅含截距项，同时有截距项和趋势项[19]。通过任一形式的ADF检验即可说明序列为平稳时间序列[16]。本文采用仅含截距项的检验模型：

式中：yt为待检验序列Y的第t时段的数值；Δyt为yt的一阶差分，即Δyt=yt-yt-1；a为常数项；b和φi为回归系数；m为滞后阶数；εt为误差项。

将普通最小二乘法下的t统计量作为ADF检验值，如果ADF检验值小于显著性水平5%下的临界值，则拒绝原假设，认为Y是平稳时间序列。如果两个时间序列没有通过平稳性检验，但两者的一阶差分序列均能通过平稳性检验且不存在协整关系，那么可以对一阶差分序列进行格兰杰因果关系检验[20]。

2.3 格兰杰因果关系检验现有研究常通过相关分析研究变量间的关系，但两个变量在统计上具有显著相关性并不意味着两者存在因果关系。本文通过格兰杰因果关系检验来分析自变量X和因变量Y之间是否存在因果关系。格兰杰因果关系检验的原理是：如果在同时考虑X和Y的前期信息的情况下对Y的预测结果显著优于只考虑Y的前期信息的情况下对Y的预测结果，说明考虑X的前期信息显著地提高了对Y的预测精度，那么X是Y的格兰杰原因[21]，存在X和Y互为格兰杰原因的现象。

格兰杰因果关系检验采用的回归模型如下[16]：

式中：yt和xt分别为序列Y和X的第t时段的数值；n为滞后阶数；αj、βj、λj、δj均为回归系数；ε1t、ε2t为误差项。

格兰杰因果关系检验的原假设是X和Y之间不存在格兰杰因果关系。计算式（2）和式（3）的F统计量及其对应的频率[22]，如果F统计量对应的频率小于显著性水平5%，则拒绝原假设，说明存在格兰杰因果关系。

在多年调节水库调蓄的影响因素分析中，如果存在格兰杰因果关系，那么最大滞后阶数N反映了影响因素的对多年调节水库调蓄的最长显著影响时长，将N作为影响时长。

2.4 多元线性回归显著性检验格兰杰因果关系检验得到的最大滞后阶数可以反映各影响因素的影响时长，但不能反映各影响因素的作用效果随时间的变化情况。为了解答这一问题，本文采用多元线性回归的F检验和t检验，量化分析各影响因素在不同时段对多年调节水库调蓄的影响程度差异，同时也作为格兰杰因果关系检验结果合理性的辅助分析方法。

建立多元回归方程：

式中：yt为因变量；h为常数项；gj为回归系数；v为自变量数量，取值为1～N；N是通过格兰杰因果关系检验的最大滞后阶数；xt-j是自变量。F检验可判断回归方程是否具有显著的线性关系，t检验可判断每个自变量是否对因变量具有显著影响。随着v的增大，F检验和t检验结果随之改变，从而反映不同时段的影响因素对回归方程线性关系及因变量的影响程度差异。

构造F统计量检验回归方程线性关系的显著性：

式中：F为多元线性回归方程的F统计量；c为样本数量；y^t为用式（4）计算出的yt的估计值；y¯t为yt的平均值。如果F统计量对应的频率小于显著性水平5%，则认为回归方程具有显著的线性关系。

构造t统计量检验回归方程中每个自变量对因变量的影响是否具有显著性：

式中：tj为多元线性回归方程自变量xt-j的t统计量；g^j为gj的估计值；ej为gj的标准误差。如果 t统计量对应的频率小于显著性水平5%，则认为自变量对因变量具有显著影响。

2.5 多年调节水库数据处理多年调节水库调度计划的制定受到来水与用水的影响。来水、用水与水库调蓄在年内均呈现出周期性变化，例如汛期来水多、非汛期来水少，农业用水集中于灌溉期，水库枯水期补水、汛期蓄水等。如果采用日尺度或月尺度数据，时间序列无法通过平稳性检验。在进行格兰杰因果关系检验时，采用年尺度数据较为合适。

水库调蓄决策的时间尺度一般小于月尺度，汛期调蓄可以达到小时尺度。如果采用年尺度数据，对水库调蓄发挥关键影响的年内前期信息会被视为当年值，导致其在格兰杰因果关系检验中被忽略。为了解决这一问题，本文对时间序列进行处理，待检验的初始时间序列为X0和Y0，构造时间序列X1和 Y1，令：

在检验X是否是Y的格兰杰原因时，对X1和Y0进行检验；在检验Y是否是 X的格兰杰原因时，对Y1和X0进行检验。采用这一处理方法可以保障来水、用水与水库调蓄在年内的前期信息不被忽略。

3 应用实例检验

3.1 研究区域与数据来源以位于黄河上游的龙羊峡水库为例进行研究。龙羊峡水库位于青海省共和县、贵南县交界处，是黄河干流上唯一一座多年调节水库，控制黄河天然径流量的40%以上，调节库容193.6亿m3（图1）。龙羊峡水库1978年开工建设，1986年开始蓄水。水库的开发任务以发电为主，兼有防洪、灌溉、防凌、养殖、旅游等综合效益。

图1 研究区域

从理论和调蓄实践分析，黄河天然径流量和地表水取水量可能是龙羊峡水库补水量的影响因素，龙羊峡水库补水量可能影响黄河取水量，但黄河天然径流量不受龙羊峡水库影响。因此，分析黄河天然径流量是否是龙羊峡水库补水量的格兰杰原因，检验黄河取水量与龙羊峡水库年补水量是否互为格兰杰原因，并根据最大滞后阶数识别影响时长。

将龙羊峡水库出库水文站贵德站和入库水文站唐乃亥站的实测年径流量之差作为龙羊峡水库的年补水量，为负值时代表水库蓄水。研究时段为1990—2018年，贵德和唐乃亥实测径流量采用相应水文站的实测数据，黄河天然径流量与取水量采用《黄河水资源公报》和第三次水资源调查评价成果。

3.2 平稳性检验结果时间序列平稳性检验结果见表1。1990—2018年黄河天然径流量、地表水取水量和龙羊峡水库补水量的ADF检验值均小于显著性水平5%时的临界值，说明均是平稳时间序列，可以进行格兰杰因果关系检验。

表1 ADF单位根检验结果

3.3 因果关系检验结果格兰杰因果关系检验结果见表2。对于原假设1，滞后阶数为1年和2年时，F统计量对应的频率小于5%，拒绝原假设，说明在考虑当年值和前1年值的情况下，天然径流量是龙羊峡水库补水量的格兰杰原因；滞后阶数为3年时，F统计量对应的频率大于5%，接受原假设，说明在考虑当年值和前2年值的情况下，天然径流量不是龙羊峡水库补水量的格兰杰原因；根据最大滞后阶数得到天然径流量对龙羊峡水库补水量的影响时长为2年。由原假设2和原假设3的检验结果可知，地表水取水量是龙羊峡水库补水量的格兰杰原因，影响时长为2年；龙羊峡水库补水量不是地表水取水量的格兰杰原因。

表2 格兰杰因果检验结果

3.4 多元线性回归显著性检验结果由于黄河天然径流量和地表水取水量均是龙羊峡水库补水量的格兰杰原因，因此对龙羊峡水库补水量及其两个影响因素分别进行多元线性回归，考虑滞后阶数为1年（即仅考虑影响因素的当年值）和2年（即考虑影响因素的当年值和前1年值），拟合效果和显著性检验结果见表3和表4。

表3 多元线性回归拟合效果与公式F检验结果

表4 多元线性回归自变量的t检验特征值的频率

对于天然径流量和龙羊峡水库补水量，在滞后阶数为1年和2年两种情景下多元线性回归的相关系数没有达到强相关性，但均高于0.3，且拟合公式均通过了显著性水平5%的F检验，说明天然径流量和龙羊峡水库补水量之间具有显著的线性关系。与滞后阶数为1年时的回归结果相比，滞后阶数为2年时相关系数增大，F检验特征值的频率减小，说明考虑天然径流量的前1年值增大了线性关系的显著性。自变量的t检验结果显示，当滞后阶数为1年时，天然径流量的当年值对龙羊峡水库补水量的当年值具有显著影响；当滞后阶数为2年时，天然径流量的当年值对龙羊峡水库补水量的当年值具有显著影响，但天然径流量的前1年值对龙羊峡水库补水量的当年值没有显著影响，说明天然径流量当年值对龙羊峡水库补水量的影响程度高于前1年值。

对于地表水取水量和龙羊峡水库补水量，在滞后阶数为1年和2年两种情景下多元线性回归的相关系数均低于0.3，虽然随着滞后阶数的增大拟合效果改善，但两种情景下拟合公式均没有通过显著性水平5%的F检验，说明变量之间的相关性很弱。两种情景下自变量的t检验特征值的频率均大于5%，说明每个自变量对因变量的影响均不显著。

4 讨论

4.1 来水与水库调蓄之间的关系分析由格兰杰因果关系检验和线性回归显著性检验结果可知，黄河天然径流量对龙羊峡水库调蓄的影响时长为2年，其中天然径流量当年值的影响大于前1年值。1990—2018年历年黄河天然径流量和龙羊峡水库补水量见图2。在统计的29年中，有12年龙羊峡水库蓄水，年均蓄水量38.44亿m3；有17年龙羊峡水库补水，年均补水量30.54亿m3。龙羊峡水库总体表现出丰水年蓄水、枯水年补水的特征，统计结果显示，可以将天然径流量470亿m3作为龙羊峡水库蓄补水的划分界限：在水库蓄水的12年中，有75%的年份天然径流量大于470亿m3；在水库补水的17年中，有71%的年份天然径流量小于470亿m3。

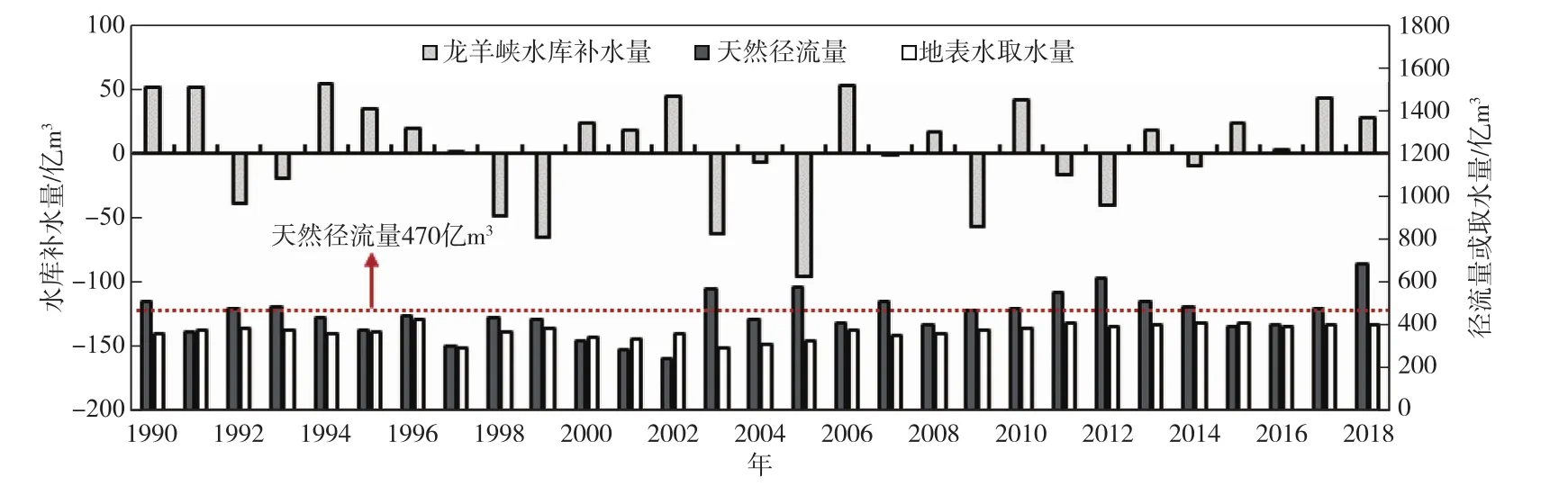
图2 龙羊峡水库补水量、天然径流量与地表水取水量变化

龙羊峡水库表现出连续蓄水和连续补水的特征，持续时间为2～3年。相关研究显示，黄河降水与径流均具有2～3年的短周期[23-24]，这与龙羊峡水库连续蓄补水特征一致。在2000—2002年连续枯水时段，黄河年均天然径流量仅289.31亿m3，比多年平均值490.04亿m3（1956—2016年系列，下同）偏低41%，期间龙羊峡水库累计补水85.35亿m3；在来水偏丰的2003—2005年，黄河年均天然径流量524.32亿m3，龙羊峡水库累计蓄水165.34亿m3。龙羊峡水库的蓄补水规律与天然径流量的丰枯特征并不完全对应，需要考虑前期影响，例如，1998—1999年黄河年均天然径流量433.28亿m3，比多年平均值偏枯12%，但龙羊峡水库蓄水113.10亿m3，原因在于1994—1997年黄河年均天然径流量仅389.89亿m3，期间龙羊峡水库持续补水，至1997年水库存蓄水量几乎耗尽，在黄河天然径流量302.25亿m3、下游断流超过200天的1997年，龙羊峡水库补水量已不足1亿m3，因此1998—1999年龙羊峡水库大量蓄水以应对未来可能发生的极端枯水。在随后发生的2000—2002年连续枯水中，1998—1999年龙羊峡水库蓄水量发挥了重要作用。

4.2 用水与水库调蓄之间的关系分析由格兰杰因果关系检验结果可知，黄河地表水取水量是龙羊峡水库补水量的格兰杰原因，影响时长为2年，但龙羊峡水库补水量不是地表水取水量的格兰杰原因；线性回归显著性检验结果显示，两者间没有显著的线性相关关系。针对两种统计分析结果相矛盾的问题，结合黄河取水和龙羊峡水库调度实践开展分析。

黄河地表水需水量主要取决于供水区的耕地面积、种植结构、人口等因素。黄河流域人均地表水资源量不足全国平均水平的1/4，是资源性缺水流域，实际供水能力远低于需水量。为了控制沿黄地区用水增长、保护黄河生态环境，1987年国务院批准实施了 “黄河可供水量分配方案”，即 “八七”分水方案，这是我国首个大江大河的水量分配方案。“八七”分水方案将黄河多年平均径流量580亿m3（1919—1975年系列）中的370亿m3分配给沿黄9省（区）及河北、天津。在实际分配中，考虑年度来水预报与水库蓄水量，对 “八七”分水方案丰增枯减得到年度省（区）分配耗水量，省（区）以分配耗水量为约束控制实际耗水量。

2001—2018水文年（当年7月至次年6月）黄河分配耗水量与实际耗水量见图3：极端枯水的2001—2002水文年实际耗水量超过分配耗水量；2003—2013水文年实际耗水量比分配耗水量小10%，年均剩余耗水指标33亿m3；2014—2017水文年实际耗水量超过分配耗水量7%，年均超指标耗水22亿m3；2018水文年来水偏丰，分配耗水量较大，实际耗水量小于分配耗水量。总体上黄河地表水耗水量在分配耗水量上下波动，呈现出先增加后减小的趋势，2010年后地表水耗水量在330亿m3附近小幅波动，地表水取水量在400亿m3附近小幅波动。

图3 黄河历年分配耗水量与实际耗水量

保障地表水的稳定供给是龙羊峡水库调蓄的重要任务，龙羊峡水库根据当年来水量和水库前期蓄水量，制定本年的蓄补水计划。1990—2018年黄河天然径流量极值比2.78，年际变化较大，龙羊峡水库在丰水年蓄水、枯水年补水，从而保障了黄河地表水的稳定供给，使地表水取水量波动幅度小于天然径流量，极值比1.46，2010—2018年极值比仅1.07（图2）。1990—2018年中有5年黄河地表水取水量甚至超过了天然径流量，这些年份龙羊峡水库均通过补水保障地表水供给，年均补水31.92亿m3。

格兰杰因果关系检验是一种统计分析方法，不涉及所检验的时间序列之间的内在作用机理，因此存在格兰杰因果关系并不意味着两个时间序列间一定具有因果关系，需要结合机制分析、实践总结等加以验证。在本文中，天然径流量是龙羊峡水库补水量的重要影响因素，但黄河地表水取水量对龙羊峡水库补水量的影响并不显著。黄河地表水取水量受到分水指标约束，总体较为稳定。龙羊峡水库根据天然径流量在年际间蓄丰补枯，是保障黄河地表水稳定供给的重要措施。