非参数化概率盒下随机与认知不确定性的分离式灵敏度分析
2023-01-31吴沐宸陈江涛夏侯唐凡赵炜刘宇
吴沐宸,陈江涛,夏侯唐凡,赵炜,刘宇,3,*
1.电子科技大学 机械与电气工程学院,成都 611731
2.中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000
3.电子科技大学 系统可靠性与安全性研究中心,成都 611731
复杂工程系统及其数值计算模型,如:飞行器及其计算流体力学(Computational Fluid Dy⁃namics, CFD)数值模拟模型,其性能响应受众多输入变量的影响[1]。工程设计人员需要从大量的输入变量中筛选出对系统响应有影响的变量,从而简化计算模型并降低计算复杂度。灵敏度分析是一种量化输入变量对输出响应不确定性贡献度的方法,可实现对输入变量的重要性排序。一方面,通过灵敏度分析可以将不重要变量固定为一个确定的常数,从而减小输入变量维数;另一方面,通过降低重要输入变量的不确定性可以大幅降低输出响应的不确定性,从而为复杂工程系统的稳健设计提供重要依据。
灵敏度分析方法主要包括以下3类[2]:局部灵敏度分析(Local Sensitivity Analysis, LSA)、区域灵敏度分析(Regional Sensitivity Analysis,RSA)和全局灵敏度分析(Global Sensitivity Analysis, GSA)。其中,全局灵敏度分析研究输入变量在整个取值域的不确定性对输出响应不确定性的影响程度[3-4],相较于局部灵敏度分析的结果更为准确,且适用于相对复杂的非线性系统。常用的全局灵敏度分析方法有扫描法[5]、微分法[6]、基于方差的灵敏度分析[7]、矩独立灵敏度分析[8]、基于信息量的灵敏度分析[9]等。
值得注意的是,现有的全局灵敏度分析方法及其拓展方法都是建立在输入变量只存在随机不 确 定 性(Aleatory Uncertainty)[10]或 认 知 不 确定性(Epistemic Uncertainty)[11]的条件上,对 于只含单一类型不确定性的输入变量可以得到较为准确的灵敏度结果。然而,由于对复杂工程系统的物理规律认识不清、待估计参数样本贫乏以及输入参数固有的随机性,随机和认知不确定性常常耦合在一起,称之为混合不确定性[12]。概率盒 模型(如图 1所示,图中p为概率;X1~X3为参数变量)是一种典型的混合不确定性量化方法,包括:参数化概率盒(Parametric P-box)和非参数化概率盒(Non-Parametric P-box)。参数化概率盒由一族同类型的累积分布函数(Cumu⁃lative Distribution Function, CDF)组成,而非参数化概率盒由边界分布包络的不同类型CDF曲线组成,其包络的分布函数的形式任意,并不局限于经典的分布函数[12],因此,在工程中应用更加广泛。本文主要针对非参数化概率盒,发展混合不确定性下的全局灵敏度指标。
要解决非参数化概率盒下全局灵敏度分析问题,首先需要解决非参数化概率盒下混合不确定性传播问题。非参数化概率盒下混合不确定性传播与概率框架下不确定性传播方法[13-14]不同,因为非参数化概率盒变量仅边界分布已知,内部包络的CDF形式均未知。近年来,学者们提出了高效的非参数化概率盒混合不确定性传播方法。Zhang等[15]提出了一种区间蒙特卡洛算法,也称作双层嵌套蒙特卡洛算法。外层对累积概率分布采样得到输入变量区间,内层通过外层采样区间内寻优获得响应概率盒的边界分布。Li等[12]提出了一种基于累积分布函数离散化的不确定性传播方法,计算响应概率盒的前4阶统计矩取值范围,并利用Johnson分布拟合[16]和基于百分数优化的方式构建响应概率盒的边界分布。本文通过双层嵌套蒙特卡洛算法得到输出响应的区间值序列,并利用经验累积概率分布[17](Empirical CDF)构建响应的边界分布。
由于非参数化概率盒模型耦合了输入变量的随机和认知不确定性,非参数化概率下的灵敏度分析挑战较大。本文将输入非参数化概率盒中的随机不确定性和认知不确定性分离,将非参数化概率盒下灵敏度分析转化为单独研究输入非参数化概率盒的随机不确定性(或认知不确定性)对系统响应的随机不确定性(或认知不确定性)的影响,从而指导后续系统参数的随机或认知不确定性降低甚至消除。然而,非参数化概率盒下构建灵敏度指标面临2大挑战:①如何分离非参数化概率盒变量的随机与认知不确定性;②如何构建指标分别衡量输入随机/认知不确定性对响应随机/认知不确定性的影响。针对挑战①,本文分别提出了基于格点法和期望值法分离非参数化概率盒的随机与认知不确定性。针对挑战②,本文将构建概率盒最大方差和面积度量指标分别衡量系统输入随机、认知不确定性对输出随机、认知不确定性的影响。最后,针对NACA0012翼型绕流问题,分析了来流参数和湍流模型设计参数中的混合不确定性,给出了相应的灵敏度分析结果和工程指导意义。
1 非参数化概率盒及其不确定性传播
1.1 非参数化概率盒
如 图2所 示,概 率 盒(Probability-Box, Pbox)是概率分布与区间的广义表现形式[18]。非参数化概率盒包络的分布函数形式任意,相较参数化概率盒更具有一般性。非参数化概率盒FX可以定义为一个五元组和为概率盒的上、下边界,概率盒包络的分布函数FX(x)隶属于概率盒空间FX,且满足关系和VFX分别为概率盒包络分布的均值和方差所属区间[19]:
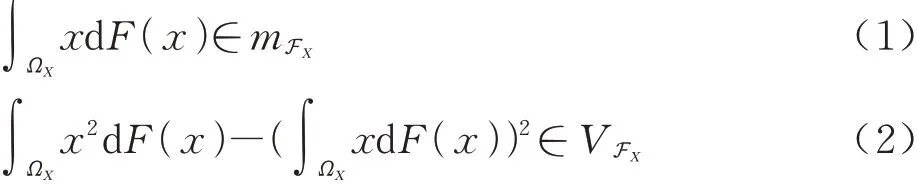
式中:ΩX为样本域。一般来说,非参数化概率盒的边界分布已知,边界分布内包络无数条非参数化的分布函数[12]。如图2所示,非参数化概率盒的 边 界 分 布 为 分 段 高 斯 分 布 函 数FX;μ,σ2(x)=N(μ,σ2):
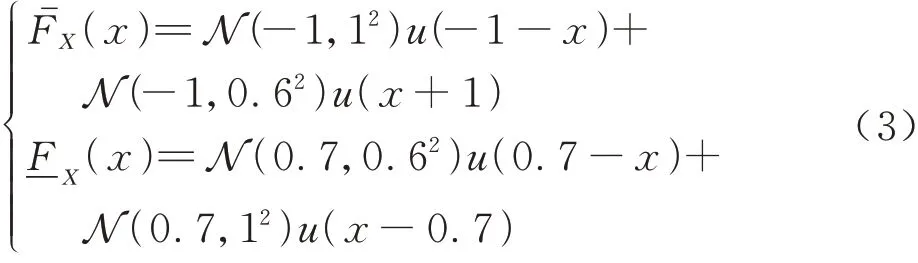
式中:u(x)为阶跃函数,x≥0时为1;否则为0。
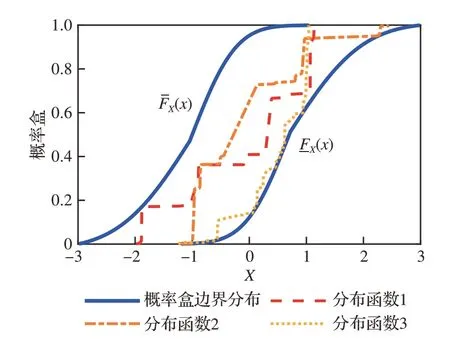
图2 非参数化概率盒示例Fig. 2 Illustration of non-parametric P-box
1.2 混合不确定性传播
假 定 系 统 响 应 函 数Y=g(X1,X2,…,Xn),输入X=[ ]X1,X2,…,Xn为非参数化概率盒向量,则系统输出响应Y的概率盒可通过双层嵌套蒙特卡洛方法得到[20]。如图3所示,双层嵌套方法包含2层循环:外层通过蒙特卡洛采样计算累积概率的笛卡尔积集p:
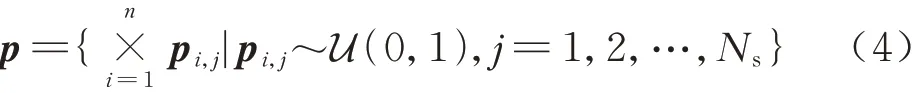
式 中:pi,j表 示 对Xi采 样 得 到 的 第j个 概 率 样 本。系统输入的区间笛卡尔积集[X]可通过p进行如下计算得到:
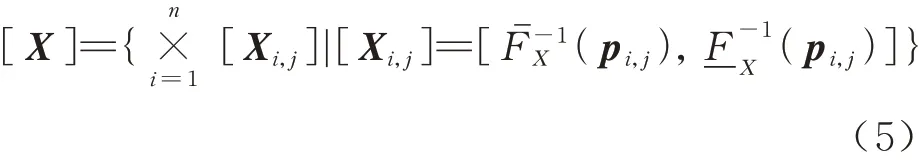
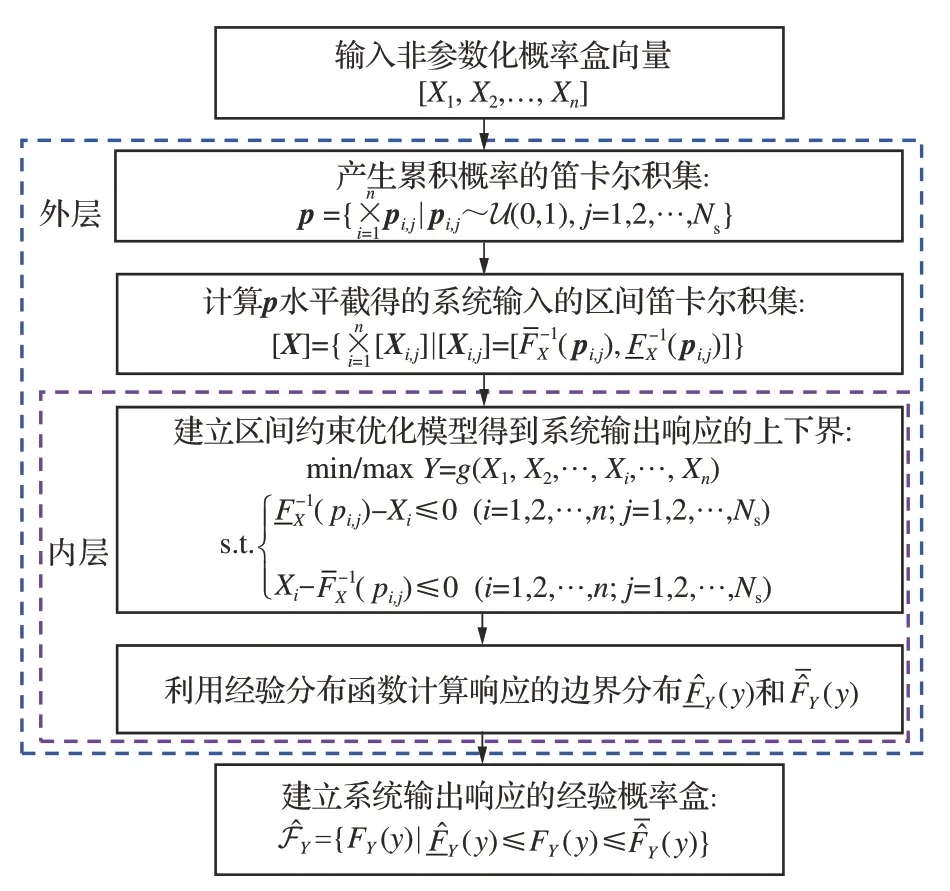
图3 非参数化概率盒下双层嵌套不确定性传播流程图Fig. 3 Double loop procedure with non-parametric Pboxes
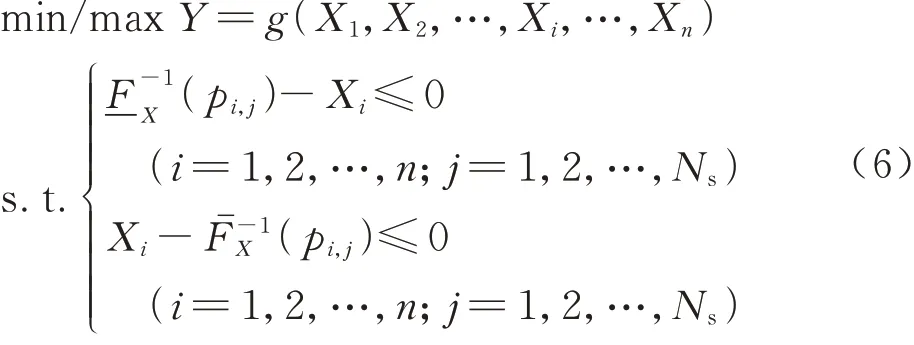
为了避免分布拟合误差[22],本文采用经验分布函数构建响应概率盒的边界分布[17]:
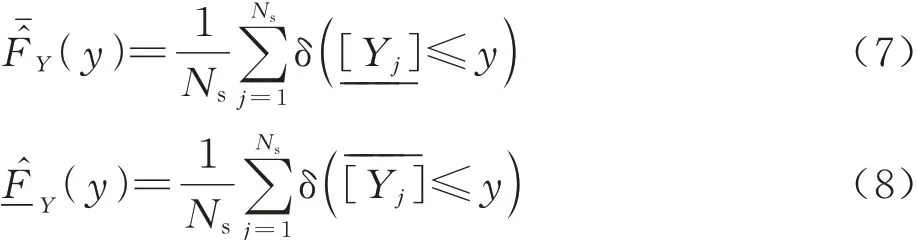
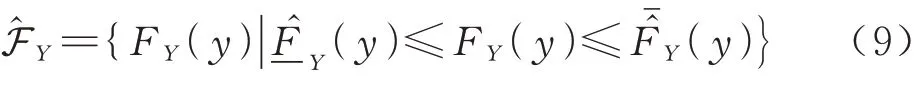
2 非参数化概率盒下随机与认知不确定性分离方法
2.1 基于期望值法的认知不确定性分离
非参数化概率盒FX由边界分布包络的任意分布形式的分布函数构成,分离FX的认知不确定性指概率盒包络的任意分布FX(x)退化为其期望值所 有EFX组 成 一 个 区 间为非 参数化概率盒分离认知不确定性的结果。显然,和即是概率盒上、下边界分布的期望。如图4所示,以式(3)定义的非参数化概率盒为例,分离认知不确定性后,概率盒退化为区间数[−1.11,0.84]。
2.2 基于格点法的随机不确定性分离
非参数化概率盒的随机不确定性分离等价于将概率盒退化为内部的一条分布函数[23]。根据分布函数性质,分离随机不确定性后得到的分布函数应满足:
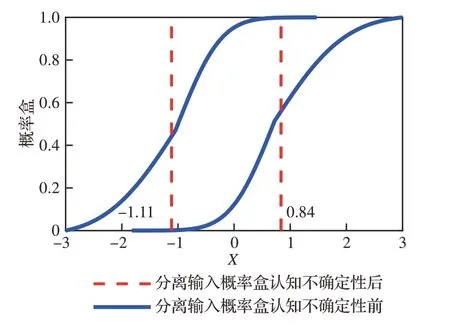
图4 非参数化概率盒认知不确定性分离示意图Fig. 4 Illustration for separating epistemic uncertainty of non-parametric P-box
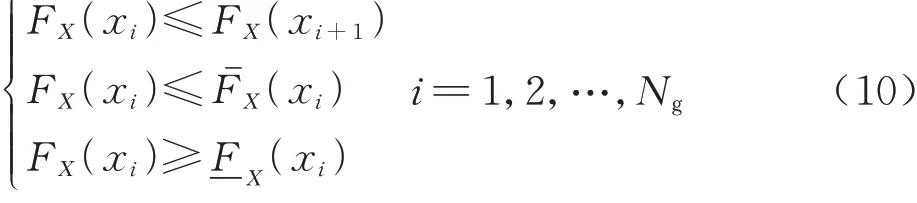
和

式中:Ng为样本数量;xi为样本取值。非参数化概率盒包络的任意分布应同时满足式(10)和式(11)。然而,由于式(10)线性不等式约束的系数矩阵为大型稀疏矩阵,直接求解式(10)和式(11)构建的可行域不可行。因此,为了高效求解非参数化概率盒分离随机不确定性后的分布函数,本文提出了基于格点法的非参数化概率盒随机不确定性分离方法。
格 点(xi,FX(xi)) (i=0,1,…,Ng+1)由 样本点xi与对应累积概率FX(xi)组成,分别称为x值和p值。如图5所示,格点法包括4个主要步骤:
步骤1 从 区 间和区间中均匀随机产生首末2个x值x0和xNg+1,通 过 轮 盘 赌 方 法[24]保 证0.5的概率得到和两个区间边界值,其余x值由等间距插值得到:

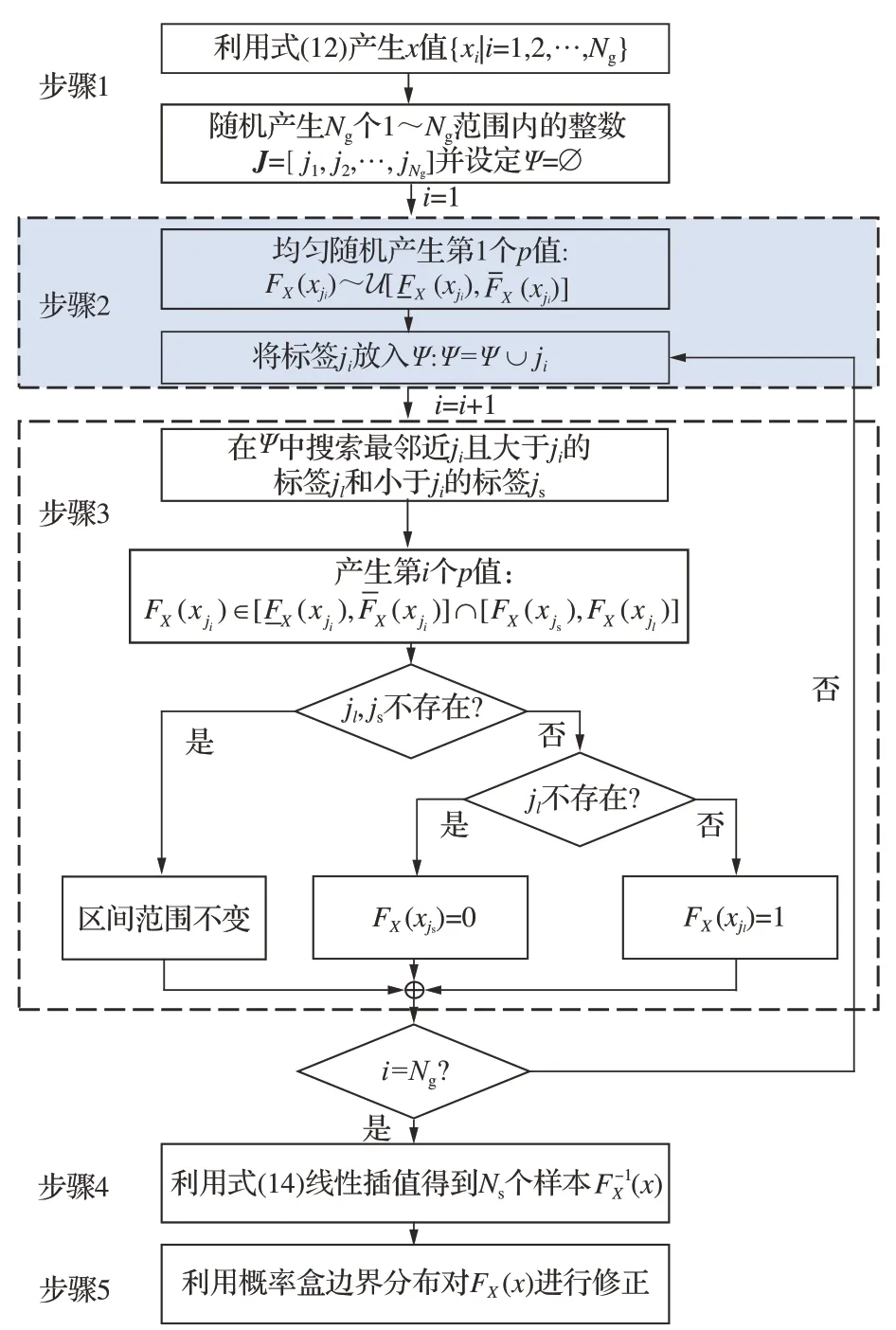
图5 基于格点法的非参数化概率盒随机不确定性分离Fig. 5 Grid point method for separating aleatory uncer⁃tainty of non-parametric P-boxes
此外,随机产生Ng个在1∼Ng范围内的整数,并用Ψ=∅存放已经产生的格点标签。
步骤2 按J中整数序列在区间FˉX(xj1)]中 均 匀 随 机 产 生 第1个p值FX(xj1),并将标签j1放入集合Ψ中。
步骤3 产生第i个p值时,在Ψ中搜索最邻近ji且大于ji的标签jl和小于ji的标签js,则第i个p值FX(xji)的取值范围:
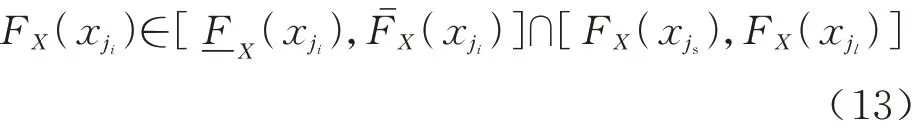
式中:当js不存在时FX(xjs)=0;当jl不存在时FX(xjl)=1。执行本步骤Ng次得到所有格点。
步骤4 将格点按标签1∼Ng的顺序顺次排列,并 加入FX(x0)=0和FX(xNg+1)=1这2个 格点,得到格点集{(xi,FX(xi))|i=0,1,…,Ng+1}。格 点 法 可 在 区 间[0,1]均 匀 随 机 产 生Ns个FX(x),通过线性插值得到FX(x)对应的样本
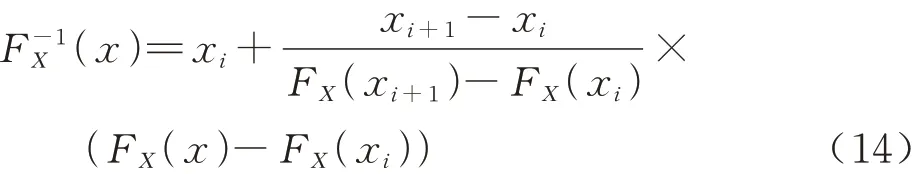
步骤5 线性插值后得到的分布函数FX(x)可能超出概率盒边界分布包络的范围。利用概率盒边界分布对FX(x)进行修正,若超出其取值范围,则将移至距离其最近的边界,保证了产生的分布函数FX(x)位于非参数化概率盒包络的范围之内。图5为格点法的示例,基于Ng=103个格点产生了3条分布函数。需要注意,分离随机不确定性后非参数化概率盒退化为非参数化概率盒内任意一条分布函数,因此结果不唯一。
3 随机与认知不确定性分离式灵敏度
3.1 基于面积的分离式灵敏度指标
考虑输入变量的认知不确定性对响应认知不确定性的影响,本文采用面积指标度量输出响应认知不确定性,构建基于面积的认知不确定性分离式灵敏度指标。图6为基于面积的输出概率盒认知不确定性量化示意图。
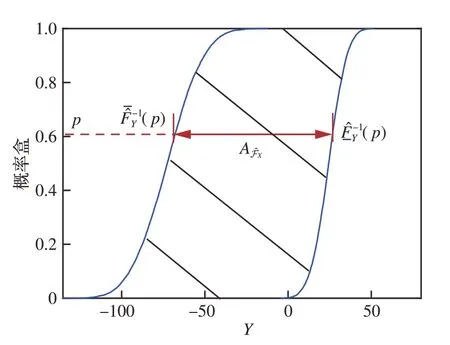
图6 输出响应的认知不确定性量化示意图Fig. 6 Quantification of output epistemic uncertainty
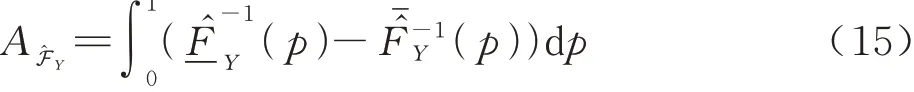
不失一般性,令Xs为输入非参数化概率盒变量,利用格点法分离Xs的随机不确定性,使Xs退化为概率盒包络的一条任意分布形式的分布函数,并通过双层嵌套不确定性传播方法构建下面的优化模型得到输出响应区间[Yj]:
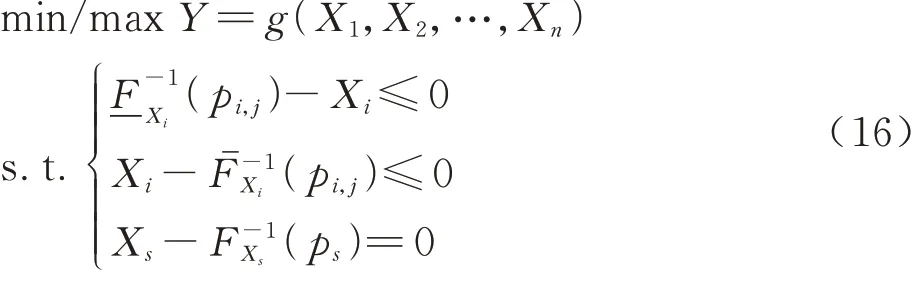
式中:s≠i;s,i=1,2,…,n;j=1,2,…,Ns。利用式(7)和式(8)可构建输出响应概率盒,进而得到分离Xs的随机不确定性后输出响应概率盒的面积:
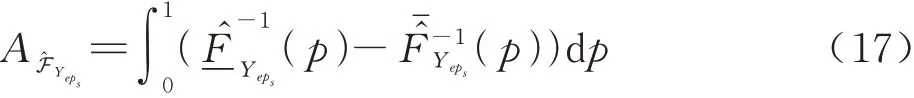

式中:Seps-ep∈[0,1]反映了输入变量Xs的认知不确定性对输出响应认知不确定性的影响,指标越大表明Xs的认知不确定性对输出响应的认知不确定性的影响越大。
由于分离输入非参数化概率盒变量中的随机不确定性结果为概率盒包络的任意一条分布函数,Seps-ep的取值不稳定。假设通过格点法产生了nep条分布函数,记nep个灵敏度指标结果为本文进一步研究指标随nep的变化规律,计算S的均值和均值的95%置信区间,选取使S的均值收敛、置信区间宽度较小的nep值,并将对应的均值作为指标Seps-ep的估计。S的均值和95%置信区间(CI)为
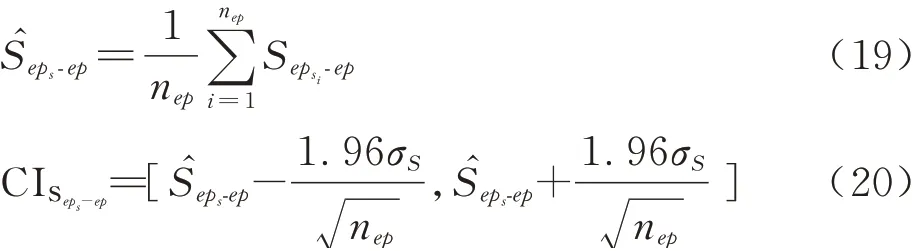
式中:σS为nep个灵敏度指标结果S的标准差:
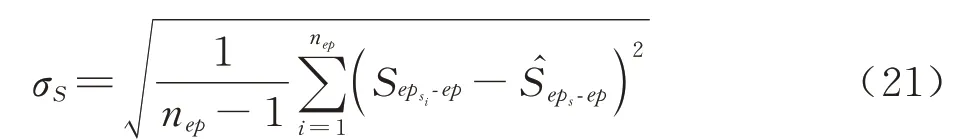
3.2 基于最大方差的分离式灵敏度指标
为了量化输入非参数化概率盒的随机不确定性对输出随机不确定性的影响,本文采用最大方差指标度量输出随机不确定性,构建基于最大方差的分离式灵敏度指标。
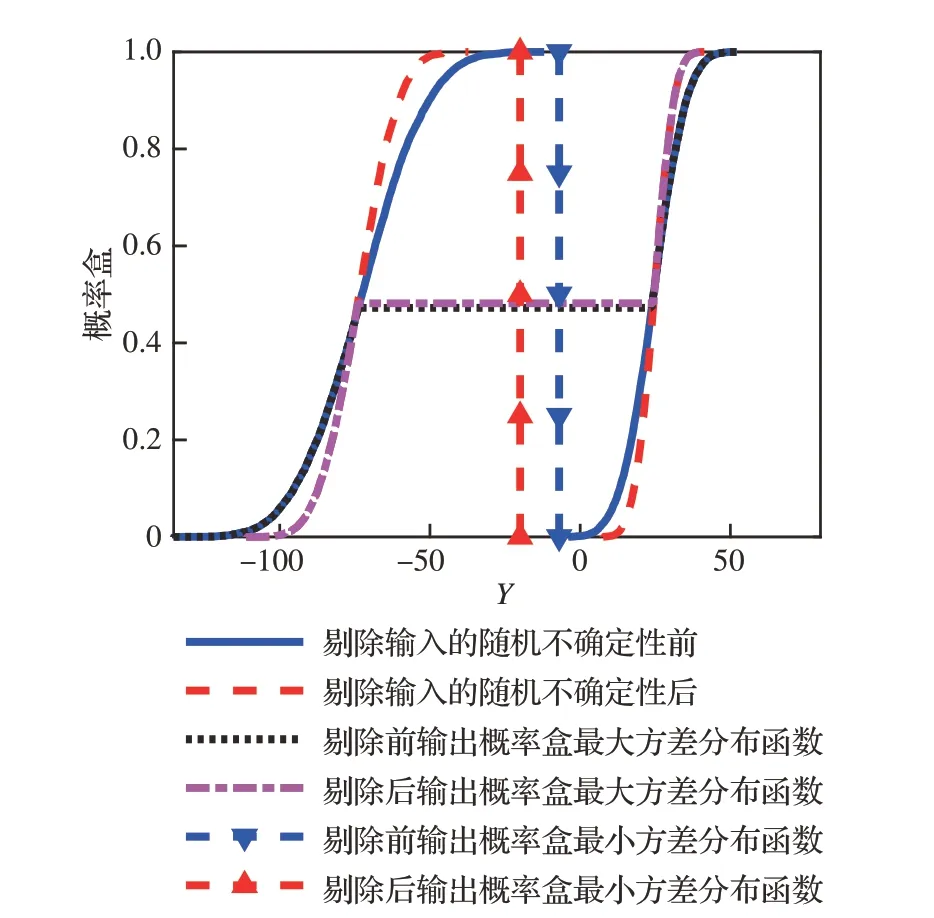
图7 输出响应概率盒的最大方差和最小方差示例Fig. 7 Maximum and minimum variances of output response
方差指标已经被广泛应用在灵敏度分析中,用于衡量输出随机不确定性的大小。对于输出为概率盒而言,其方差为一个包含最大值与最小值的区间数[19]。本文将概率盒方差的上界定义为概率盒最大方差,将概率盒方差的下界定义为概率盒最小方差,如图 7所示。然而,并非概率盒最大方差和最小方差都适用于衡量输入非参数化概率盒的随机不确定性对输出随机不确定性的影响。原因在于用于衡量输入概率盒的随机不确定性对输出随机不确定性的指标必须满足单调性,即:降低任意输入概率盒的随机不确定性,量化输出概率盒的随机不确定性指标必须满足单调不增。显然概率盒最小方差指标不满足该单调性。如图7所示,分离输入概率盒的认知不确定性后,输出的概率盒更加“立陡”(图 7中红色虚线包含的概率盒),其随机不确定性必然降低,但是通过计算发现,最小方差在分离输入认知不确定性前后始终为0,灵敏度指标不变。因此,概率盒最小方差不能用作衡量输入非参数化概率盒的随机不确定性对输出随机不确定性的影响。而最大方差在分离输入概率盒的认知不确定性后会降低,能够有效评判输入的随机不确定性对输出随机不确定性的影响。因此,本文提出建立基于概率盒最大方差的分离式灵敏度指标。
求解概率盒的最大方差等价于求解概率盒的一条分布函数,并使其方差最大,本文称该分布函数为“最大方差分布函数”。式(10)表明难以通过遍历概率盒的任意分布求解其最大方差。因此本文提出了一种高效的最大方差求解方法。分布的方差可通过生成[0,1]间均匀分布的概率样本,经逆分布函数采样获得。令p(j)(j=0,1,…,Ns)为均匀分布概率样本由小到大排列的顺序统计量,则响应的方差为
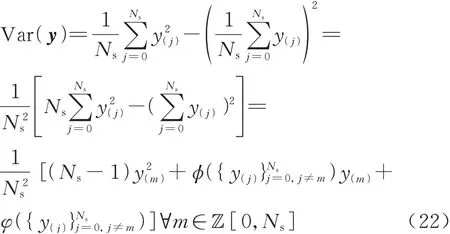
式中:y(j)为p(j)通过逆分布函数采样得到的输出样本和为 样 本集的函数:
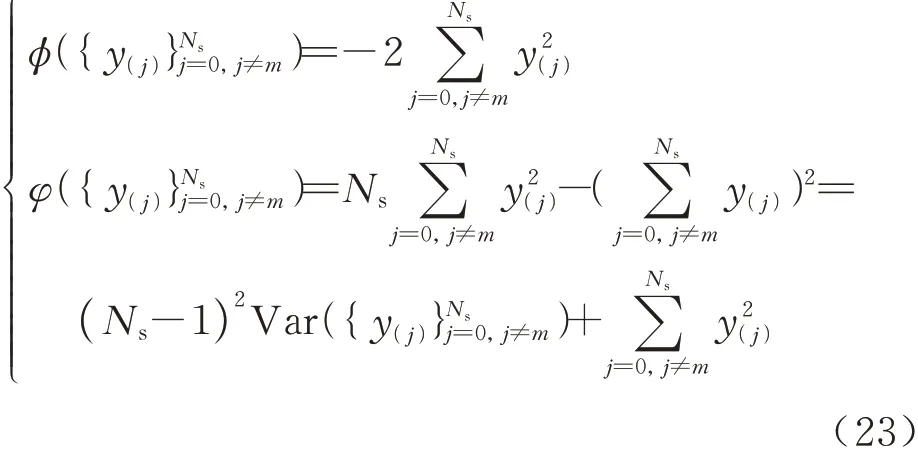
式(22)表明,输出响应的方差是样本y(m)的二次函数,而因此当且仅当全部样本y(j)取值为其边界时,才能得到概率盒的最大方差。考虑到最大方差分布函数需满足单调递增性以及离散程度尽可能大2个要求,如图 8所示,最大方差分布应由3段分布函数组成:(ⅰ)当y∈[y(0),y(k)]时,输出响应概率盒的上边界时,累积概率位于 区 间均 匀 分 布 函 数;(ⅲ)当y∈[y(k+1),y(Ns)]时,输出响应概率盒的下边界至此,遍历式(10)的可行域求解最大方差的问题简化为求解跳跃点y(k)的问题。
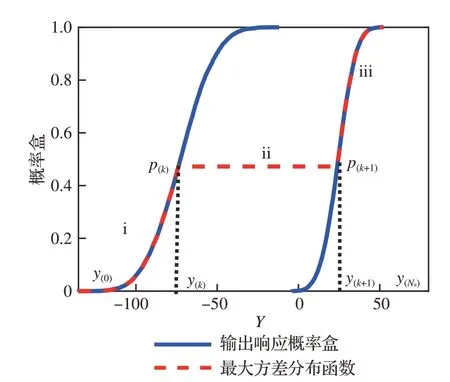
图8 输出响应概率盒最大方差示意图Fig. 8 Maximum variance of output response
下面将阐述概率盒最大方差的求解过程:首先由式(6)产生了Ns+1个输出响应区间第ⅱ段的累积概率可通过端点累积概率p(k)和p(k+1)进行线性插值得到,则各段的累积概率为
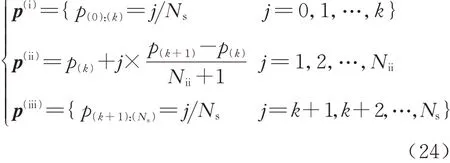
式中:Nii表示第ⅱ段含有的累积概率值个数,取决于第ⅱ段的累积概率p(k+1)−p(k):
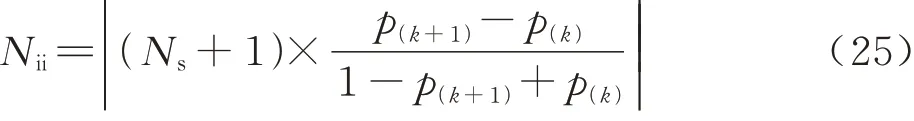
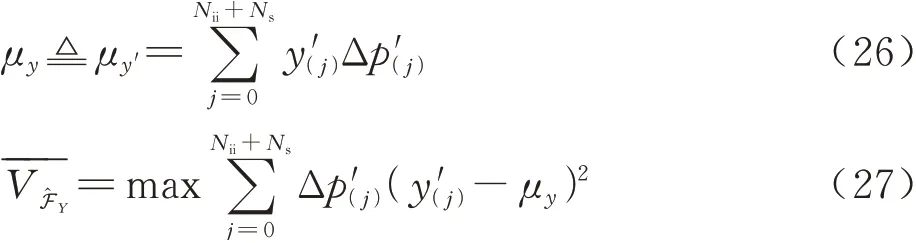
进一步地,以式(27)为目标函数构建优化模型,寻找方差最大时的跳跃点y(k)以及对应的最大方 差
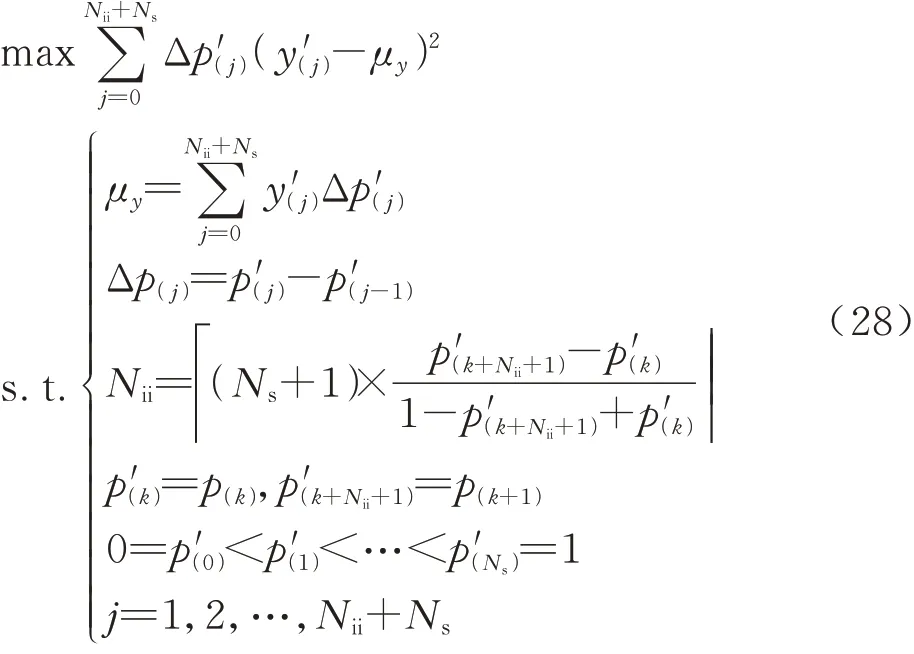
分离输入非参数化概率盒变量Xs的认知不确定性使概率盒FXs退化为概率盒边界分布期望组成的区间数[EFˉXs(x),E-F Xs(x)],并利用双层嵌套不确定性传播计算输出响应区间[Yj]:
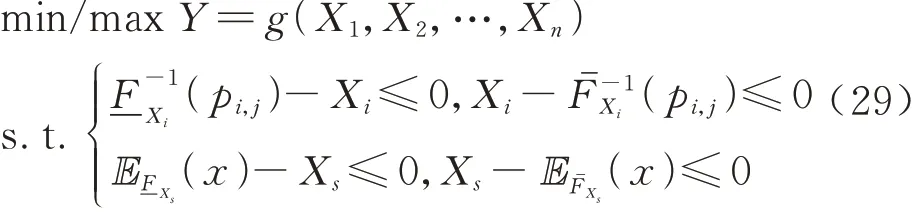
式 中:s≠i;s,i=1,2,…,n;j=1,2,…,Ns,利用式(7)和式(8)构建输出响应概率盒并利用式(28)计算分离输入非参数化概率盒变量Xs的认知不确定性后输出概率盒的最大方差。令表示输入变量Xs的认知不确定性分离前输出响应概率盒的最大方差,则基于最大方差的分离式灵敏度指标定义为

其中,Sals-al∈[0,1]反映了输入变量Xs的随机不确定性对输出响应随机不确定性的影响,指标越大表明Xs的随机不确定性对输出响应的随机不确定性的影响越大。
4 算例分析
4.1 数值算例
本算例采用简单的多项式方程验证本文所提出分离式灵敏度分析方法的正确性。具体的,有如下响应函数:

式中:X1~X3均为非参数化概率盒变量,如表1所示。表1中列举了Case1~Case5共5种类型概率盒边界分布,分别是高斯分布N(μ,σ2)、对数正态分布LN(μ,σ2)、伽玛 分布Γ(a,b)、多峰高斯分布[14]以 及 包 含 前3种 分 布 形式的混合边界分布。设定2层嵌套不确定性传播方法外层采样量为Ns=105,格点法产生Ng=103个格点,随机选择nep=600条分布函数曲线,分别计算5种边界分布形式下的分离式灵敏度指标的均值和Sals-al(s=1, 2, 3),结果如图 9所示。从图中可以看出,分离输入随机不确定性和分离认知不确定性的灵敏度排序结果分离均为X3>X2>X1。输入X3的随机不确定性和认知不确定性分别对输出Y的随机不确定性和认知不确定性的影响最大,而输入X1的随机不确定性和认知不确定性分别对输出Y的影响都是最小的。
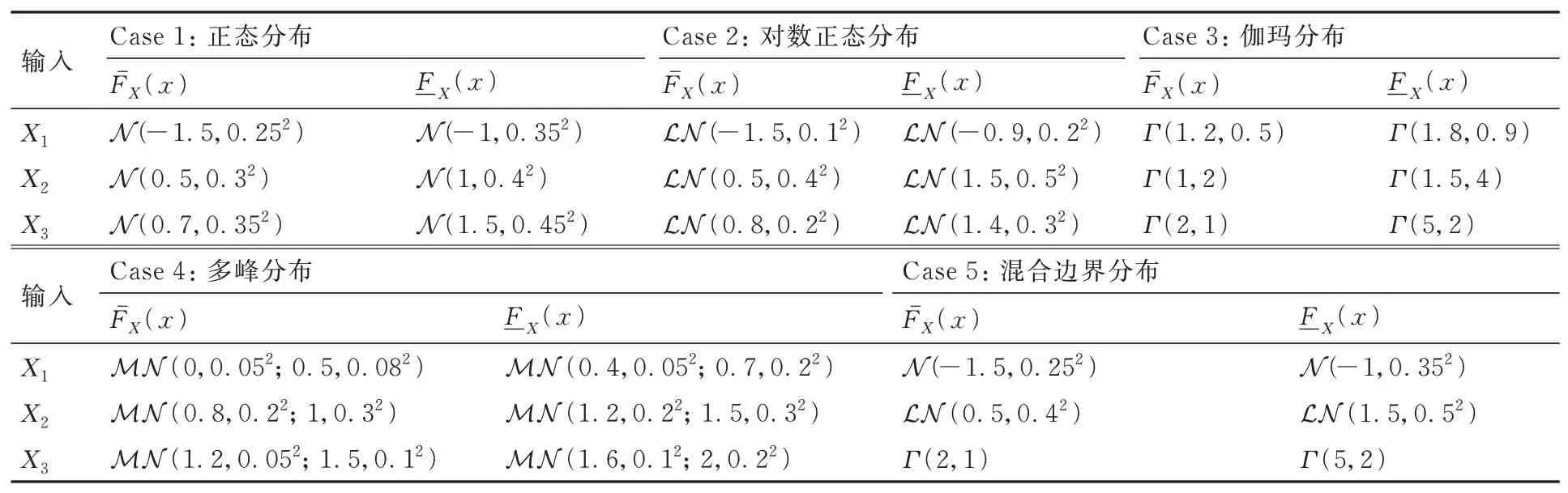
表1 输入非参数化概率盒变量的边界分布Table 1 Boundary distributions of input non-parametric P-box variables
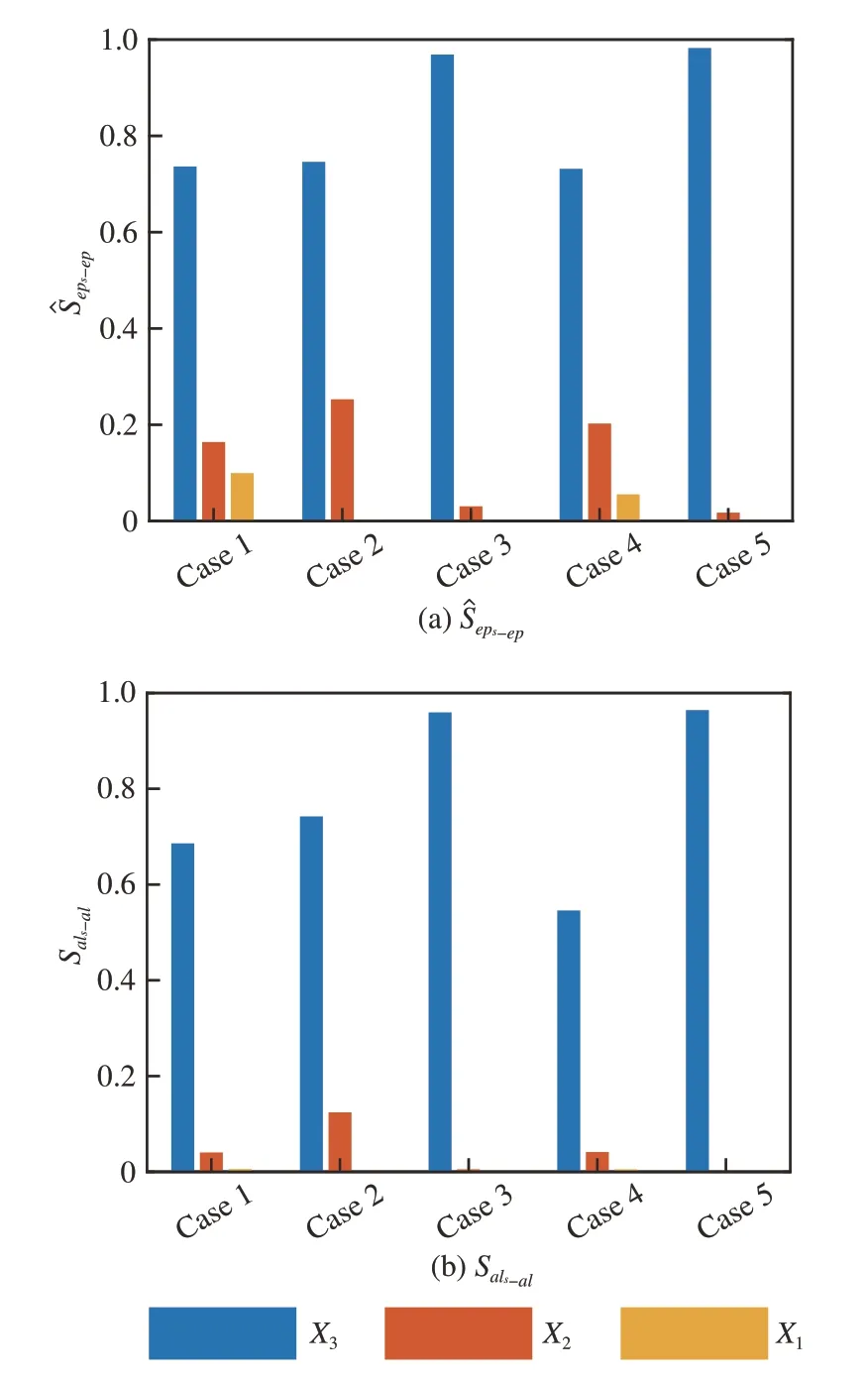
图9 5种边界分布形式下分离式灵敏度指标Fig. 9 Separating sensitivity analysis indices for five boundary distribution types
4.2 NACA0012翼型绕流模拟
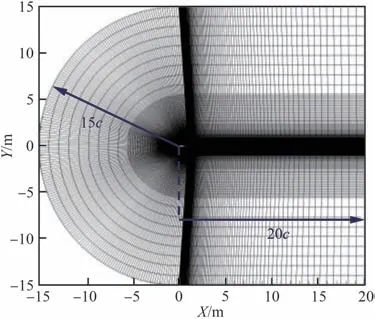
图10 NACA0012翼型绕流模拟网格划分Fig. 10 Grid setup of flow over NACA0012 airfoil simulation
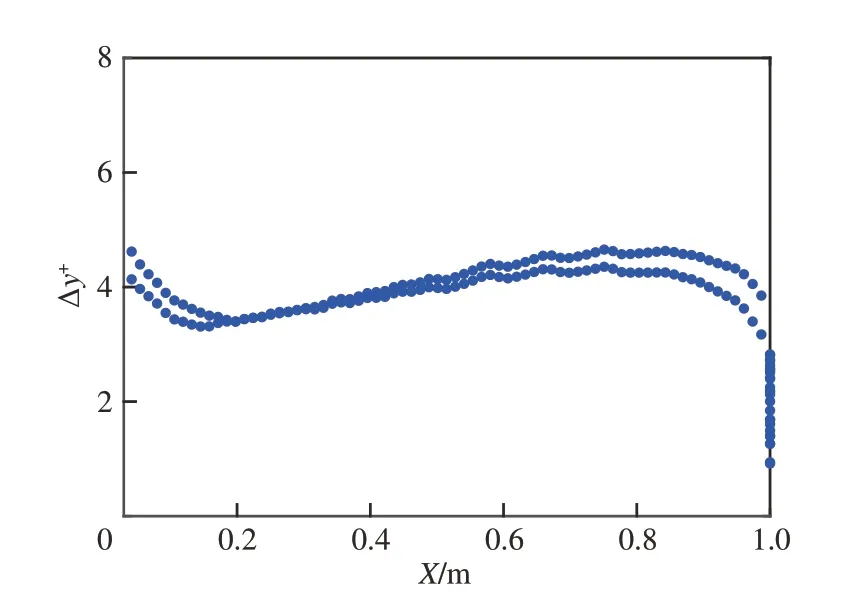
图11 无量纲壁面距离求解Fig. 11 Dimensionless wall distance resolution
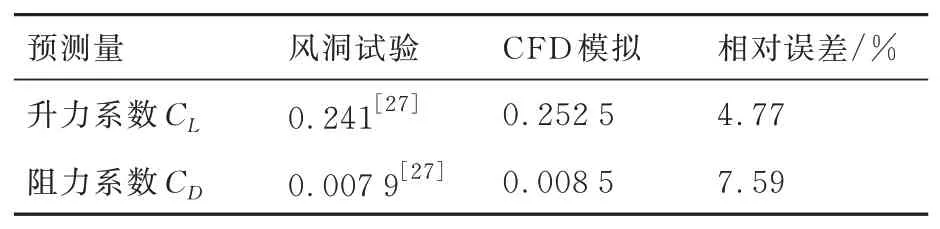
表2 CFD升阻系数预测与风洞试验对比Table 2 Comparison between CFD results and wind tunnel test data
本文提出的分离式灵敏度分析方法将应用于NACA0012翼型关键气动参数升阻比的预测,分析来流参数和湍流模型参数的混合不确定性对升阻比预测结果不确定性的影响。图10为NACA0012二维绕流模拟网格划分。利用ANSYS/ICEM CFD19.0软件构建总格点数为203×216的C型网格,其中翼型表面共有208个格点,近壁面第1层网格高度为2×10−6。翼型的弦长c=1 m,前缘和后缘分别距离上游流场、下游流场的距离为10c和20c。首先,给定自由来流马赫数Ma∞=0.7,迎角α=1.55°,雷诺数Rec=9×106,来 流 静 温T=288.15 K,采 用Spalart-Allmaras一 方 程 湍 流 模 型[25],利 用ANSYS/FLUENT19.0计算无量纲壁面距离Δy+。Δy+的计算结果如图11所示,可以发现最大无量纲壁面距离为4.63,满足Δy+<5的黏性底层的条件[26],并预测升阻系数与风洞试验结果[27]对比如表 2所示。通过表 2发现,本文构建的CFD模型预测结果与风洞试验结果误差较小,该CFD模型可以用于计算翼型气动参数。由于翼型绕流包含激波-边界层分离、转捩等复杂的空气动力学现象,采用确定性的湍流模型参数往往会带来较大的预测误差[28]。同时,真实飞行过程中翼面绕流机制较为复杂,存在大气紊流和阵风而对自由来流马赫数和迎角等来流参数产生一定干扰,因此来流参数也存在不确定性[29]。考虑到来流参数受大气扰流的影响,同时经典湍流模型参数的标定来源于试验、假设或专家经验,因此,实际工程中,来流参数和湍流模型参数用混合不确定性变量描述更加贴切。本文将NACA0012绕流模拟的边界条件设定为来流参数(自由来流马赫数Ma∞和迎角α)和Spalart-Allmaras一方程湍流模型参数[25](卡门常数κ和cv1等5个参数),输出为升阻比CLCD。NACA0012翼型绕流模拟模型由ANSYS/FLUENT19.0构建,采用基于压力的耦合算法,梯度计算采用格林高斯节点方法,使用二阶迎风Roe格式计算无黏通量[30]。由于求解一次数值解的时间过长,不利于不确定性量化与传播,因此本文采用Kriging模型[31]代替FLUENT求解器构建数值模型,并利用风洞试验[27]测得的394组升阻比数据近似代替CFD仿真模型验证代理模型的预测精度,计算平均绝对百分比误差为7.73%。表 3为来流参数、湍流模型参数非参数化概率盒的边界分布,其中湍流模型参数的试验标定和取值范围由文献[32]给定。本文采用的2层嵌套不确定性传播方法外层采样量[33]为Ns=105,得到输出升阻比概率盒如图12所示,并利用式(15)和式(28)计算输出升阻比概率盒的面积和最大方差,分别为10.738 0和86.973 9。

表3 NACA0012绕流模拟边界条件设置Table 3 Boundary condition setup for flow over NACA0012 airfoil simulation
下面构建基于面积的分离式灵敏度指标。格点法产生Ng=103个格点,利用式(14)进行线性插值得到分离概率盒随机不确定性后的分布函数曲线。如图 13所示,假定nep=200∼1 000,按式(19)~式(21)求解表 3中7个参数的nep个灵敏度指标结果S的均值和95%置信区间。
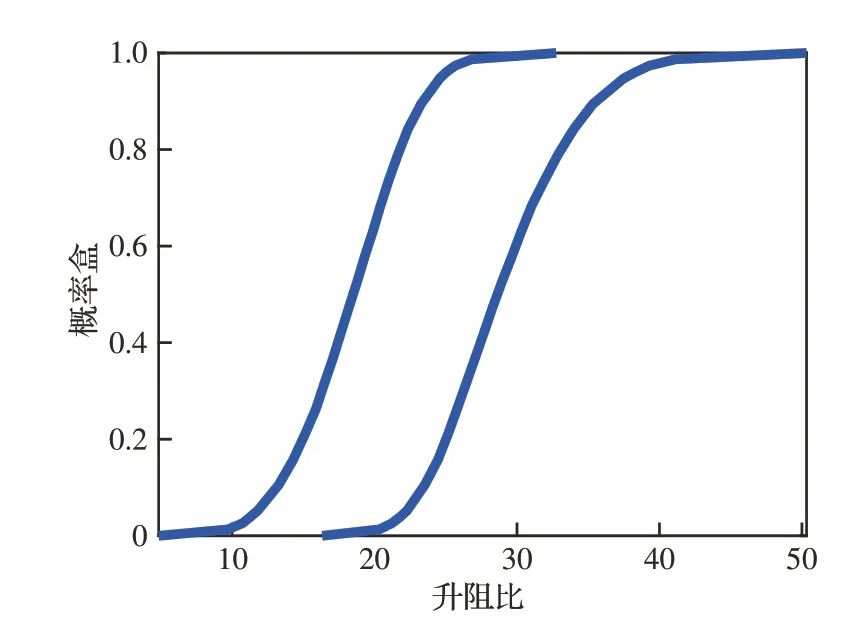
图12 输出升阻比的概率盒Fig. 12 Output lift-to-drag ratio P-box
从图 13中可以发 现,当nep=600时,S的 均值收敛且置信区间宽度较小。因此,本算例将随机选择nep=600条分布函数曲线开展后续灵敏度分析。单独分离表 3给出的7个参数的随机不确定性,得到输出升阻比概率盒如图 14所示。构建式(18)中的基于面积的分离式灵敏度指标,以nep=600时S的 均 值Ŝeps-ep作 为 灵 敏 度 指 标 的 估计,并给出均值的95%置信区间宽度WCISeps−ep,如表4所示。从表4中可以发现,自由来流马赫数Ma∞和迎角α是对输出响应升阻比的认知不确定性贡献最大的2组模型输入参数,表明采用阵风减缓等措施以减小自由来流马赫数的认知区间,同时利用颤振主动抑制减小迎角的浮动范围对降低升阻比预测结果的认知不确定性有显著影响。针对湍流模型参数,κ,cv1,cb1,cw2的影响均比较显著,但相对来流参数对升阻比的认知不确定性影响较弱,有必要重点考虑卡门常数κ和cv1的认知不确定性对升阻比的认知不确定性的影响。同时,分别单独分离表 3给出的7个模型参数的认知不确定性,得到输出升阻比概率盒如图15所示,建立式(30)中的基于最大方差的分离式灵敏度指标Sals-al(s=1,2,…,7)。表5说明自由来流马赫数Ma∞和迎角α依旧是最主要的2个模型参数,它们的随机不确定性对升阻比的随机不确定性影响最大。湍流模型参数中κ,cw2,cv1,cb1的影响均比较显著,需要重点考虑卡门常数κ的随机不确定性对升阻比的随机不确定性的影响。
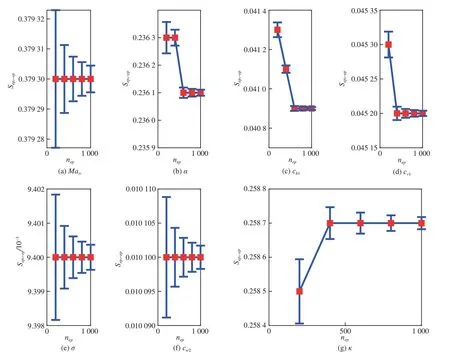
图13 灵敏度指标Seps-ep的均值和95%置信区间Fig. 13 Mean value and 95% confidence interval of sensitivity analysis indexSeps-ep
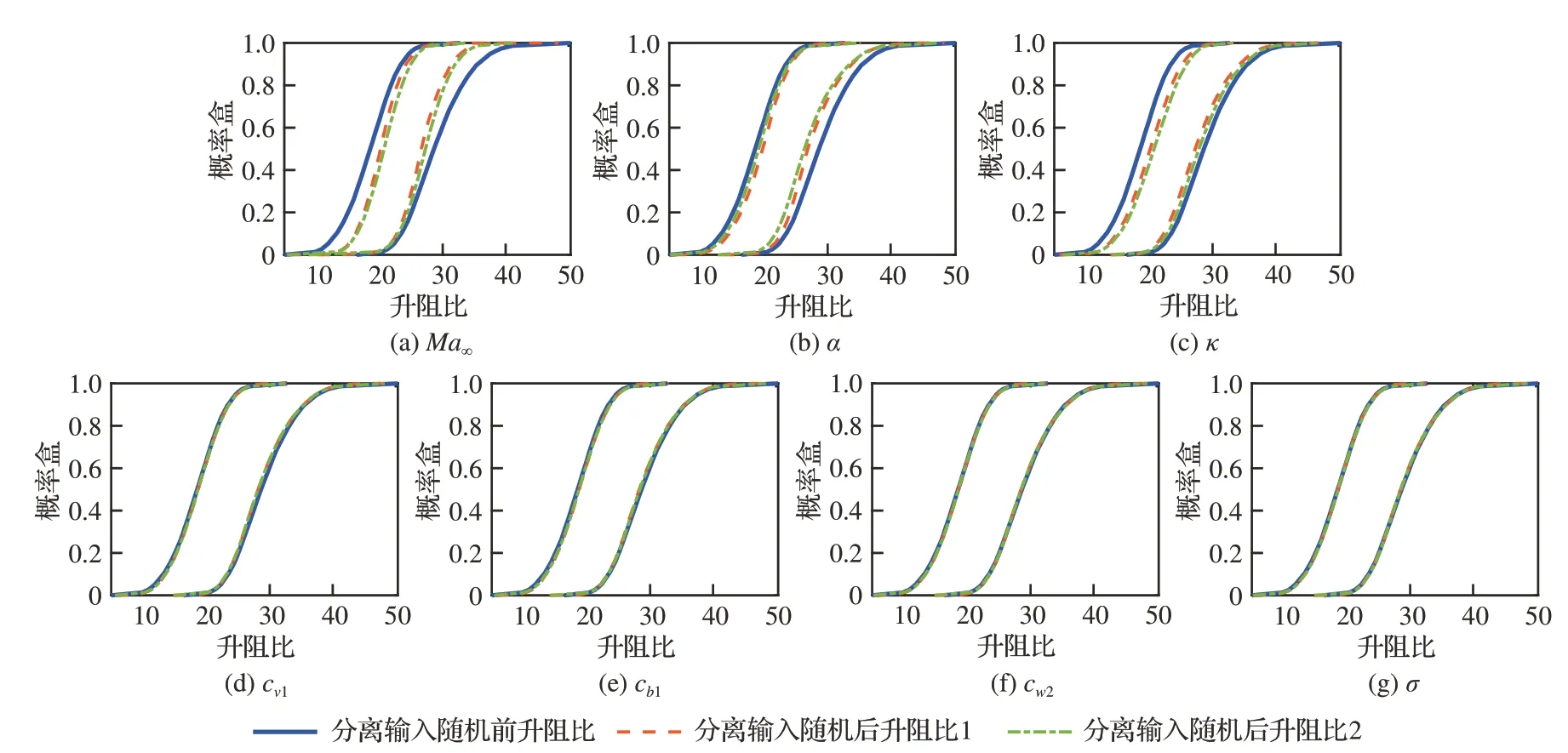
图14 分离输入参数的随机不确定性前后输出升阻比的概率盒Fig. 14 Lift-to-drag ratio before and after separating aleatory uncertainty of input parameters
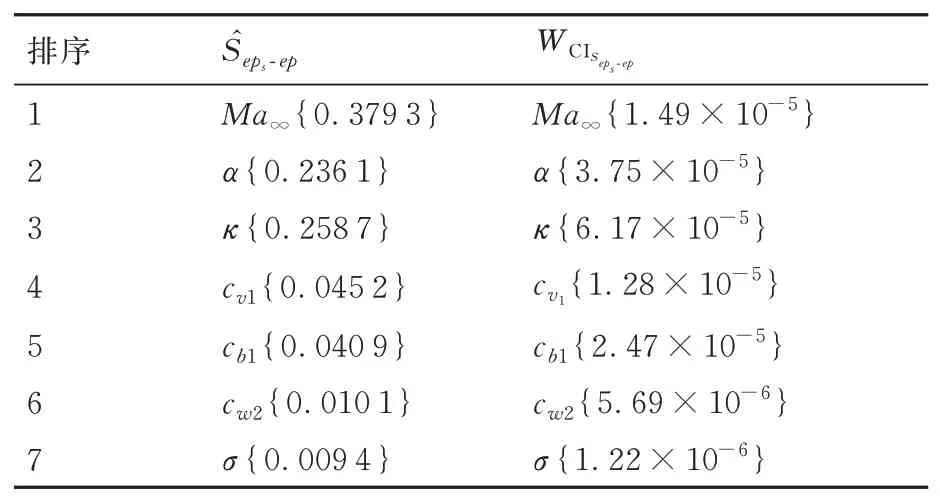
表4 基于面积的分离式灵敏度分析结果Table 4 Separating sensitivity analysis results based on area metric
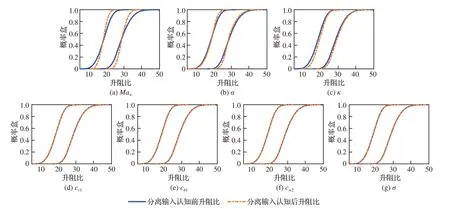
图15 分离输入参数的认知不确定性前后输出升阻比概率盒Fig. 15 Lift-to-drag ratio before and after separating epistemic uncertainty of input parameters

表5 基于最大方差的分离式灵敏度分析结果Table 5 Separating sensitivity analysis results based on maximum variance metric
综合表 4和表 5的结果,可以得出来流参数的不确定性是影响升阻比预测结果不确定性的关键因素,湍流模型参数的不确定性对升阻比的影响相比来流参数较小但不可忽略,这是因为Spalart-Allmaras模型参数综合影响了涡黏性系数的生成、扩散和耗散,而涡黏性系数是基于雷诺平均方程一类湍流模型中模化湍流量的关键参数,将影响通过数值模拟预测升阻比的结果。在湍流模型参数当中,有必要重点关注卡门常数κ和参数cv1,cw2的不确定性对升阻比预测结果的不确定性的影响。本文所提方法指出了来流参数和一部分湍流模型参数的不确定性对升阻比预测结果的不确定性存在一定影响,对于灵敏度排序靠后的湍流模型参数,可以通过赋常数值等处理方法,降低数值模拟的计算量。例如,按表 4和表 5的灵敏度排序,从低到高将重要性排名较低的湍流模型参 数σ,cw2,cb1,cv1赋为其试验标定值 (如表 3所示),计算输出升阻比概率盒的面积和最大方差,并计算和未赋常数时升阻比概率盒的面积和最大方差的相对误差,结果如表6所示。可以发现,分别将湍流模型参数σ和cw2以及同时将σ和cw2赋为试验标定值时,升阻比概率盒的面积和最大方差相较未赋试验标定值的情况相对误差都不超过3%。表明σ和cw2的认知、随机不确定性对升阻比的影响非常小,可以赋为常数。而其他参数赋为试验标定值时,输出的相对误差都超过3%,不能简单赋为试验标定值处理。因此,本文所提出方法可以降低复杂系统的计算负担。
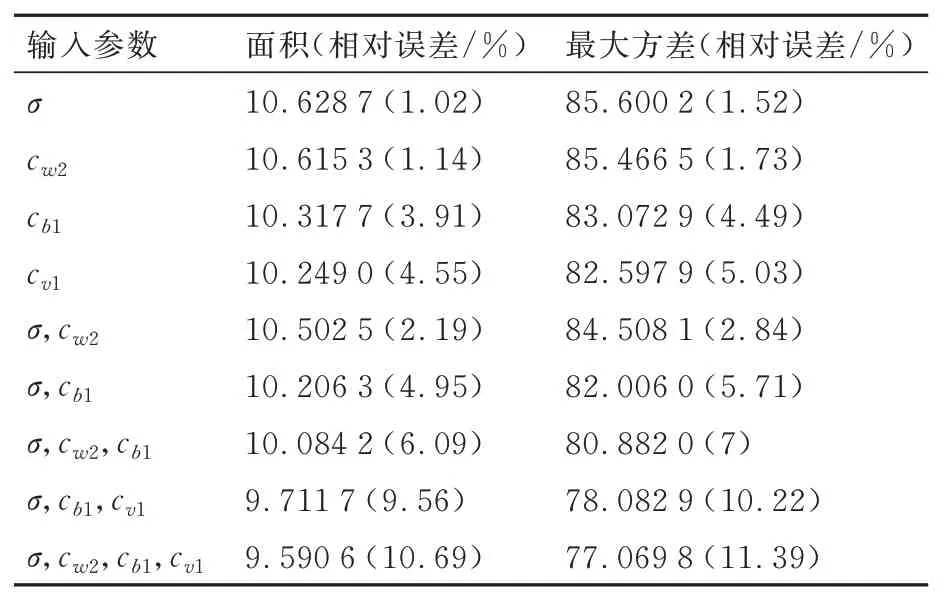
表6 输入参数赋为试验标定值时输出概率盒的面积和最大方差以及相对误差Table 6 Comparison of lift-to-drag P-box’s area and maximum variance after and before setting in⁃puts as constants
同时,对比同一组输入参数的随机和认知不确定性对升阻比预测的影响结果如表 7所示。表 7说明同一湍流模型参数的随机不确定性成分与认知不确定性成分对系统的不确定性贡献并不完全一致。因此,工程中需要将混合不确定性参数的随机和认知不确定性分离,分别研究其对输出结果的影响,才能为后续混合不确定性降低提供决策依据。

表7 输入参数的随机和认知不确定性成分对升阻比预测结果的影响对比Table 7 Comparison of effects of aleatory and epis⁃temic uncertainties on lift-to-drag ratio
此外,文献[20]提出了一种不分离随机和认知不确定性下灵敏度分析方法。该方法利用巴氏距离统一量化输出的随机和认知不确定性,通过巴氏距离的变化量化输入参数对输出概率盒的灵敏度结果。将本文所提出的2个分离式灵敏度指标结果与巴氏距离结果进行对比,如表 8所示。可以发现,文献[20]的灵敏度排序与分离认知不确定性的灵敏度排序相同,而与分离随机不确定性的灵敏度排序并不相同。这是因为巴氏距离度量了概率盒上下边界分布间距,侧重于量化输出概率盒的认知不确定性。通过对比可以说明,分离输入变量混合不确定性中的随机与认知不确定性成分更能区分输入参数的随机、认知不确定性成分对输出的贡献差异。
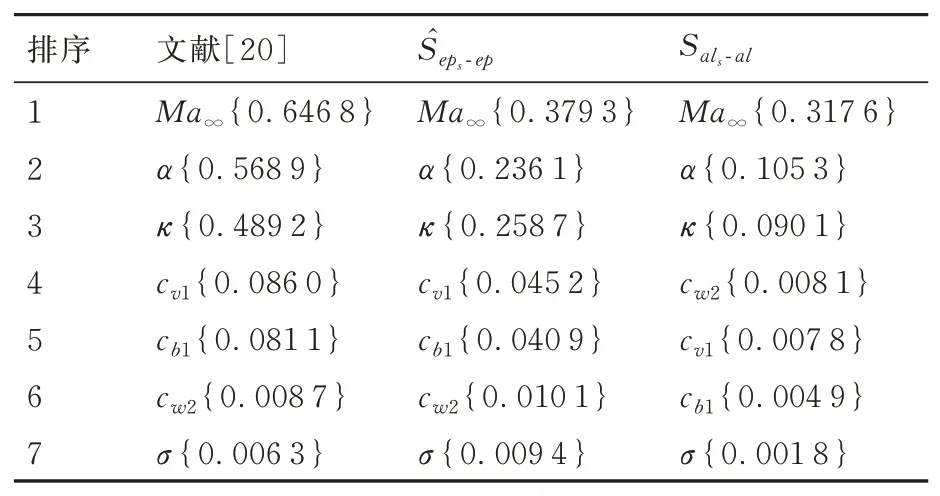
表8 本文方法与文献[20]中的灵敏度方法对比Table 8 Comparison of proposed method and reported method in Ref.[20]
5 结 论
1)提出了非参数化概率盒下随机与认知不确定性分离式灵敏度分析方法。分离输入非参数化概率盒变量的随机和认知不确定性成分,分别研究输入随机和认知不确定性对输出随机和认知不确定性的影响。
2)构建了非参数化概率盒下基于格点法的随机不确定性分离方法和基于期望值的认知不确定性分离方法,可有效地分离输入参数混合不确定性中随机和认知不确定性成分。
3)提出了基于面积和概率盒最大方差的灵敏度指标,说明了利用概率盒最大方差构建灵敏度指标的合理性,并通过与传统方法对比说明构建分离式灵敏度指标的优势。
