短舱防冰系统三维内外流耦合计算方法

2023-01-31郑梅冯丽娟秦娜尹金鸽

航空学报 2023年1期

郑梅，冯丽娟，秦娜，尹金鸽

中国航发商用航空发动机有限责任公司，上海 200241

当飞机穿越由过冷水滴组成的云层时，迎风部件表面会发生结冰现象［1-3］。发动机短舱进气道表面产生的冰聚集会改变发动机进气流场和进气流量，可能导致发动机推力下降、喘振或失速［4］；当表面积冰发生破碎时，冰片可能被吸入发动机内部，撞击风扇叶片，造成发动机机械损伤，严重危害飞行安全［5-7］。目前，在役的民用航空发动机普遍采用热气防冰结构，其中笛形管热气防冰系统由于其结构简单、可靠性强、技术成熟度高等优点，被广泛应用在发动机短舱进气道上［8-9］。在短舱笛形管热气防冰系统设计过程中，防冰性能仿真分析是设计流程的一个重要环节，构建有效的防冰计算方法可以大幅提升设计效率，为防冰性能评估及防冰结构优化设计提供支撑。

笛形管热气防冰系统的性能仿真涉及复杂的内外流耦合传热［10-13］。基于防冰系统的运行环境与工作原理，防冰腔内、外流动换热特性差异显著［14-18］，为仿真计算带来较大难度。文献中关于笛形管防冰系统的耦合仿真大多针对机翼防冰腔构型［19-23］，所采用的耦合计算方法可分为强固耦合方法［24-25］和松散耦合方法［26-27］。强固耦合计算通常将防冰腔外流域、固体域及内流域进行一体化网格划分，在计算过程中同时求解内外流场及固体域导热［28-29］；而松散耦合方法则通常将计算域进行拆分并选取合适的迭代策略以实现内外流域的耦合计算。由于松散耦合并不要求内外表面网格节点完全一致，因此在减少计算网格和提升计算效率上具有较大优势［30］。对于短舱进气道笛形管防冰系统，由于全环模型尺寸大、笛形管上射流孔数多，且进气道型面具有周向非对称特性，无法参考机翼模型截取一段直翼防冰腔进行模拟。综合计算网格与计算效率等因素，松散耦合方法更为适用。松散耦合迭代过程中涉及内外流计算域耦合面的数据交互。相较于干空气条件，湿空气条件下防冰表面热质传递过程更为复杂，且进气道表面还需考虑周向非对称流场导致的三维溢流效应对防冰表面热载荷的影响。

基于此，针对短舱全尺寸模型的笛形管热气防冰系统，采用松散耦合方法开展了三维防冰内外流仿真计算方法研究。将三维短舱进气道计算模型中的外流场独立为一个计算域，将蒙皮固体域与防冰腔内流场组合为另一个计算域，以防冰腔蒙皮外表面作为两个计算域的耦合面，通过耦合面温度和换热系数（Heat Transfer Coeffi⁃cient， HTC）相互赋值为边界条件来实现内外流计算域的数据交互。根据防冰计算流程，依次构建干、湿空气条件下的防冰内外流松散耦合迭代策略，并在湿空气条件下引入短舱周向非均匀性对防冰表面溢流流动换热特性的影响。最终获得迭代收敛后的短舱进气道防冰腔内外表面温度及换热系数分布。

1 三维防冰内外流耦合计算方法

1.1 防冰计算流程

通常，防冰计算流程包括以下3个步骤：流场计算、水滴撞击特性计算和防冰热分析计算。

1.1.1 流场计算

采用ANSYS Fluent商用软件进行流场计算，通过求解三维、定常、黏性流动的Navier-Stokes （N-S）方程，获得防冰腔外部冷空气流场、防冰腔内部热空气流场以及蒙皮固壁温度场。此时，为干空气条件下的流场计算，防冰腔内、外表面对流换热系数均可通过CFD方法计算得到。其中，防冰腔外表面对流换热系数以外流场环境温度为参考温度换算得到；而防冰腔内表面对流换热系数则以热气总温作为参考温度进行提取。

1.1.2 水滴撞击特性计算

水滴撞击特性计算采用欧拉法［31］，引入水滴相体积分数，通过求解水滴相控制方程获得水滴运动轨迹及防冰腔外表面局部水收集系数分布。

水滴相的连续性方程和动量方程可描述为

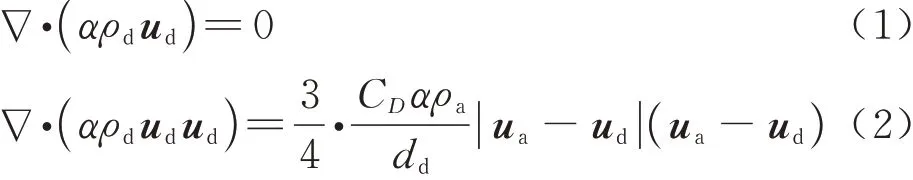
式中：α为水滴相体积分数；ρd为水滴密度，由于水滴是不可压缩的，因此式（1）中水滴密度项可约去；ud为水滴速度；CD为阻力系数；ρa为空气密度；dd为水滴直径；ua为空气速度。

根据定义，表面局部水收集系数β的计算公式为

式中：n为表面撞击位置的单位法向量；α∞与u∞分别为远场区域位置水滴相体积分数和气流速度。

将水滴相控制方程展开为Fluent用户自定义标量方程形式，采用Fluent自带的求解器，实现水滴相x、y、z方向速度与水滴相体积分数的迭代求解。

1.1.3 防冰热分析计算

防冰热分析计算采用改进的Messinger模型，考虑过冷水滴撞击防冰腔外表面后未完全蒸发而形成的溢流流动影响，但暂不考虑防冰不足导致溢流冰形成的情况。此时防冰腔外表面的热质传递如图1［32］所示。

对于防冰腔外表面任意控制体积，在稳态情况下均满足质量守恒与能量守恒，即

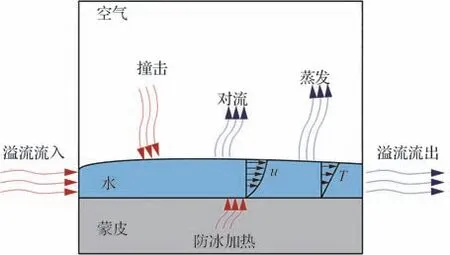
图1 考虑溢流水流动的防冰腔外表面热质传递［32］Fig.1 Heat and mass transfer on external surface of anti-icing chamber considering runback flow［32］

式中：为溢流流入质量流量；为过冷水滴撞击质量流量；为溢流流出质量流量；为蒸发质量流量；为防冰系统外表面加热量；为水滴撞击带入的总焓值，包括水滴撞击动能及水滴自身所携带的焓；为溢流流入带入的滞止焓；为表面对流换热量；为表面蒸发带走的总焓值；为溢流流出带走的滞止焓。以上各项具体表达式详见文献［32］。

由于防冰表面溢流流动主要受气动剪切力与表面压力梯度驱动，在短舱进气道周向非对称流场的作用下，会呈现较强的三维特性。如图2所示，图中CVi为控制体积，Ai为面法向量，为流入当前控制体积的质量流量，为流出当前控制体积的质量流量，i=1,2,…,4，j=1,2，防冰表面任意控制体积与其相邻的上下游控制体积之间可能存在多个溢流流入流出面，每个面上的流入流出质量流量可根据质量守恒并结合气流流动特性计算得到。

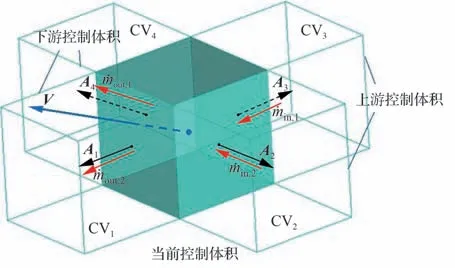
图2 三维防冰表面溢流分配示意图Fig.2 Schematic of runback distribution on 3D antiicing surface

通过Fluent用户自定义函数（User-Defined Functions ，UDFs），将水滴撞击、溢流流动及表面蒸发等能量源项引入Fluent计算的能量方程中，根据能量守恒在给定的防冰腔外表面温度边界条件下求解表面加热量Q̇anti⁃icing，wet。

以外流环境温度为参考温度，根据防冰腔外表面加热量换算得到湿空气条件下防冰腔外表面等效换热系数：

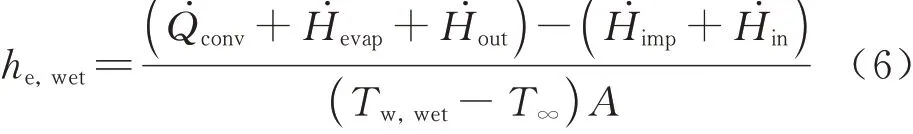
式中：Tw，wet为湿空气条件下防冰腔外表面温度；T∞为外流场环境温度；A为换热面积。

考虑固体域导热，稳态情况下防冰腔内外表面达到热平衡：

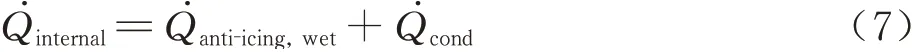
式中：为防冰腔内表面对流换热量；为固体域导热量。湿空气条件下防冰腔内表面对流换热系数计算方法与干空气条件下保持一致，仅防冰腔外表面热载荷发生变化，由此可迭代得到湿空气条件下防冰腔固体域温度场。

1.2 内外流松散耦合迭代策略

1.2.1 干空气流场计算

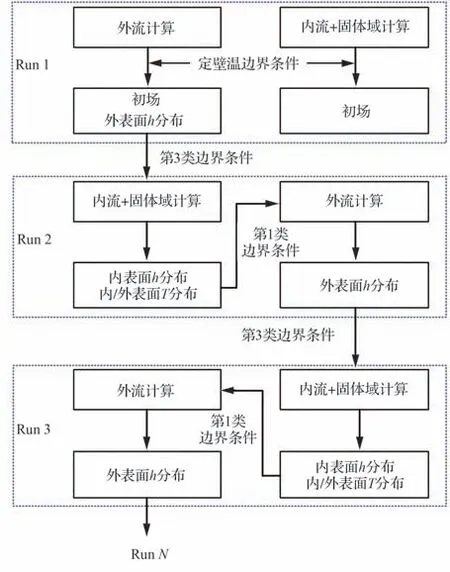
图3 干空气流场计算的内外流松散耦合迭代策略Fig.3 Loose-coupling iterative strategy of internal and external flow for flow calculation under dry air condition

干空气条件下内外流松散耦合迭代策略如图3所示，每一迭代轮次中均包含外流计算、内流与固体域计算。除第1轮次（Run 1）为初场计算外，其余轮次（Run 2~N）内均先开展内流与固体域计算后再进行外流计算。同一迭代轮次内，内外流耦合的数据交互为：内流与固体域计算获得的防冰腔外表面温度分布赋值给外流计算作为第2类边界条件。相邻轮次耦合迭代计算的数据传递为：前一轮次（RunN−1）外流计算获得的防冰腔外表面对流换热系数分布作为后一轮次（RunN）内流与固体域计算的第3类边界条件。计算过程中，不断更新防冰腔外表面对流换热系数分布与温度分布，当相邻迭代轮次的表面平均温度偏差不超过±0.5 ℃时，可判定迭代收敛。

1.2.2 湿空气防冰热分析计算

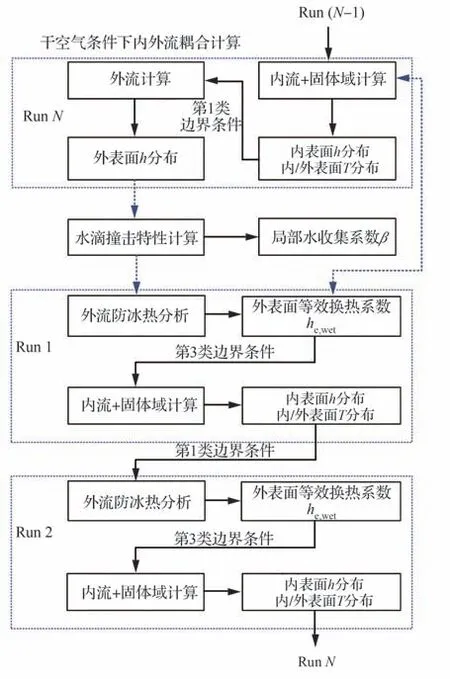
图4 湿空气流场计算的内外流松散耦合迭代策略Fig.4 Loose-coupling iterative strategy of internal and external flow for flow calculation under wet air condition

湿空气条件下，内外流松散耦合迭代策略如图4所示。以干空气条件下内外流耦合计算的收敛结果作为初场，引入水滴撞击对防冰表面换热特性的影响，外流流场计算的同时还需开展防冰表面热分析计算。同一迭代轮次中，先开展外流防冰热分析计算，提取防冰腔外表面等效换热系数作为第3类边界条件赋值给内流与固体域计算。相邻迭代轮次中，传递的数据则为内流与固体域计算获得的防冰腔外表面温度分布。在反复多次耦合迭代后，不断更新防冰腔外表面参数，迭代收敛依据仍为相邻迭代轮次防冰腔外表面平均温度偏差不超过±0.5 ℃。

2 计算模型与网格划分

2.1 计算模型与计算域

短舱笛形管热气防冰系统三维全尺寸模型如图5所示。将短舱所处外流域独立为一个计算域，防冰腔固体域和内流域合并为另一个计算域。以防冰腔蒙皮外表面作为两个计算域的耦合面，通过耦合面数据交互实现内外流域的耦合迭代。根据计算域拆分方式，依次完成外流计算域和内流计算域的网格划分。

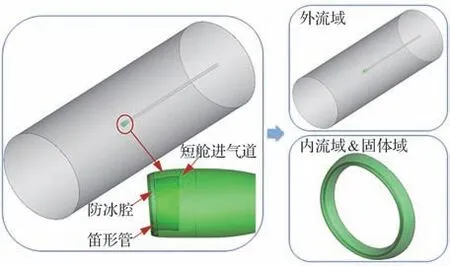
图5 计算模型与内外流计算域Fig.5 Computational model and computational do⁃mains of internal and external flow

2.2 外流计算域网格与边界条件

采用ANSYS ICEM软件对计算域进行网格划分。外流计算域网格如图6所示，总网格数约444万。为了准确模拟附面层内的复杂流动特性，短舱及其延长段的近壁面网格均进行了局部加密处理，附面层第1层网格高度约为0.01 mm，保证壁面y+≈1，网格尺度与选用的剪切应力输运（Shear Stress Transfer， SST）κ-ω湍流模型相匹配；另外，在进气道唇口附近等流场参数变化较为剧烈的区域也适当进行了网格加密处理。

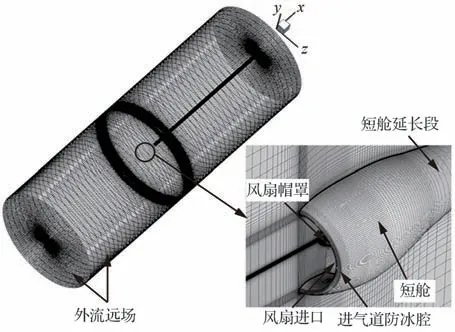
图6 外流计算域网格Fig.6 Mesh for external computational domain

外流计算域边界条件设置如下：外流边界为压力远场；风扇进口为压力出口；进气道防冰腔外表面为内外流松散耦合迭代时的数据交互面，尽管该表面边界类型始终为壁面边界条件，但赋值的温度分布会随迭代轮次不断更新；除上述边界以外，其余均为绝热壁面。

外流计算选用密度基求解器，流域中空气物性参数选用理想气体模型进行计算。松散耦合迭代过程中每一轮次的外流计算均同时监控流场残差、防冰腔外表面平均换热系数及风扇进口流量，计算收敛后流场结果才可用于后续迭代。计算的收敛标准为各残差指标下降3个数量级或残差曲线不再下降，并且外表面平均换热系数和风扇进口流量保持稳定。

2.3 内流计算域网格与边界条件

内流与固体域组成的计算网格如图7所示。为精确模拟热气由射流孔喷射冲击至防冰腔内表面的过程，需对每个小孔的射流方向及其沿程周向进行网格局部加密。同时，由于防冰腔内表面射流冲击流动换热特性较为复杂，为提高计算精度，需对内表面近壁面网格也进行局部加密，第1层网格高度约为0.01 mm，确保壁面y+与SSTκ-ω湍流模型相匹配。三维全环模型的内流与固体域计算网格总数约为1 822万。

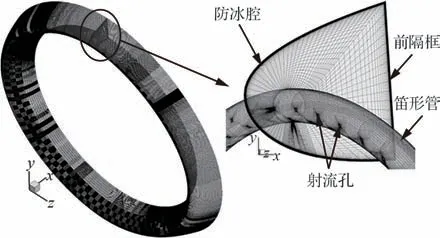
图7 内流计算域网格Fig.7 Mesh for internal computational domain

内流与固体域计算边界条件如下：防冰腔和前隔框的内表面均为流固耦合面；前隔框外表面为绝热壁面；笛形管管壁为定壁温边界条件；管壁上均布的射流孔为压力入口边界条件；防冰腔外表面仍为内外流松散耦合计算的数据交互面，壁面边界条件赋值的换热系数也会随耦合迭代过程不断更新。

内流与固体域计算时，同样选用密度基求解器，流域中热空气物性参数选用理想气体模型进行计算。松散耦合迭代过程中每一轮次内流与固体域计算均同时监控流场残差和防冰腔外表面平均温度。计算的收敛标准同样要求流场残差与监控的表面参数收敛曲线保持不变。

2.4 计算工况

计算工况如表1所示，包括飞行状态参数、结冰气象条件以及射流孔出流参数。

表1 计算工况Table 1 Computational conditions

3 计算结果与分析

3.1 算例验证

截取短舱进气道12点钟方向局部模型，依次开展强固耦合计算与松散耦合计算，通过对比分析以验证本文松散耦合计算方法及耦合迭代策略的有效性。图8为验证模型的几何及计算网格。

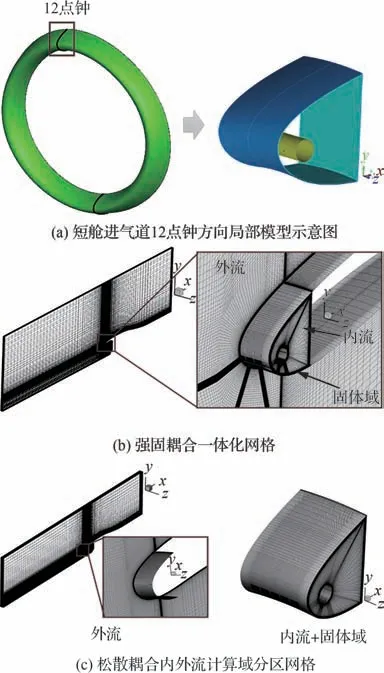
图8 计算方法验证模型及网格Fig.8 Model and mesh for computational method validation

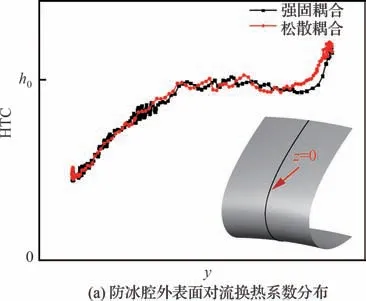
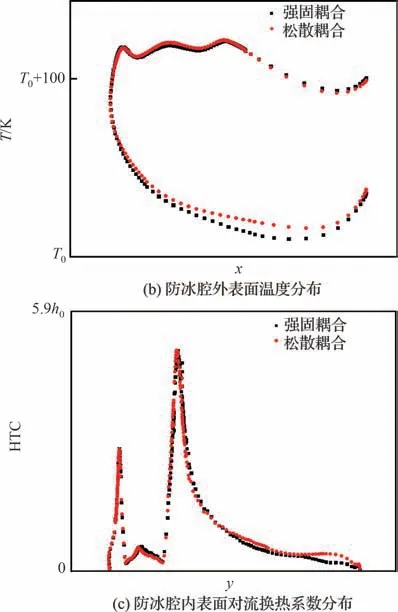
图9 干空气条件下强固耦合与松散耦合计算结果对比（z=0）Fig.9 Comparison between tight-coupling and loosecoupling methods under dry air condition （z=0）

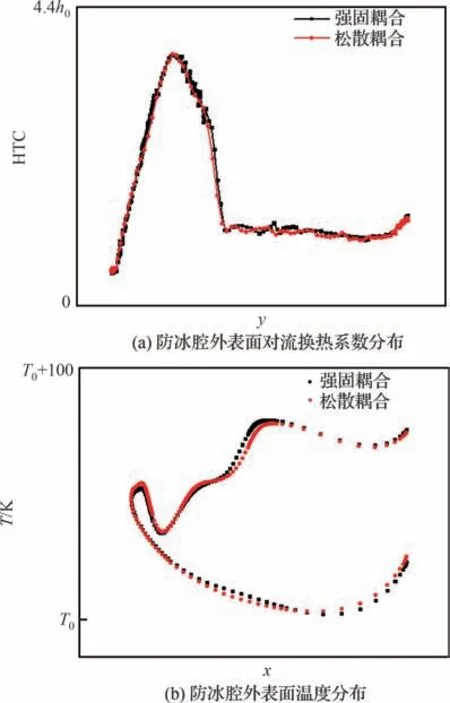
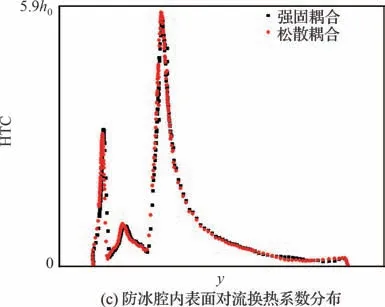
图10 湿空气条件下强固耦合与松散耦合计算结果对比（z=0）Fig.10 Comparison between tight-coupling and loosecoupling methods under wet air condition （z=0）

图9和图10分别为干、湿空气条件下强固耦合计算方法与松散耦合计算方法的对比结果，其中h0为对流换热系数基准值，T0为温度基准值，图9所示干空气条件下松散耦合计算结果为迭代3个轮次后的收敛结果，图10所示湿空气条件下计算结果为迭代4个轮次后的收敛结果。可以看出两种计算方法所得到的防冰腔内外表面各参数基本保持一致。由此可知，所采用的松散耦合计算方法及迭代策略可以达到与强固耦合计算方法基本一致的仿真精度。

3.2 干空气流场

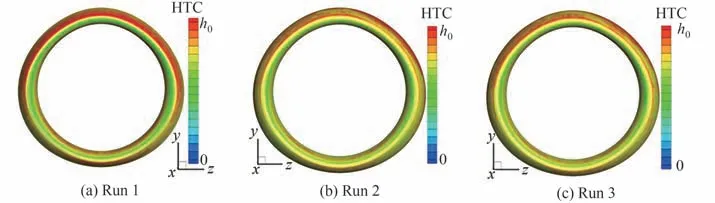
图11 干空气条件下短舱进气道防冰腔外表面对流换热系数分布Fig.11 Convective heat transfer coefficient distributions on external surface of nacelle inlet anti-icing chamber under dry air condition

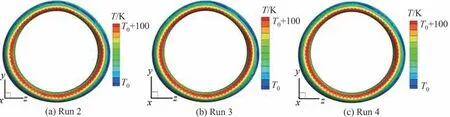
图12 干空气条件下短舱进气道防冰腔外表面温度分布Fig.12 Temperature distributions on external surface of nacelle inlet anti-icing chamber under dry air condition

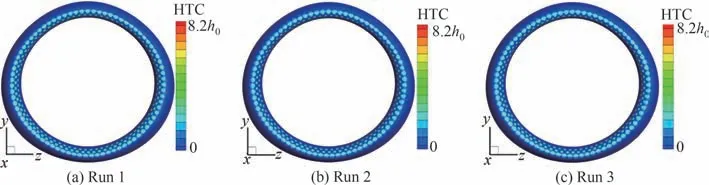
图13 干空气条件下短舱进气道防冰腔内表面对流换热系数分布Fig.13 Convective heat transfer coefficient distributions on internal surface of nacelle inlet anti-icing chamber under dry air condition

图11~图13为干空气条件下短舱进气道笛形管防冰腔外表面对流换热系数、温度以及内表面对流换热系数在内外流松散耦合不同迭代轮次下的计算结果。在经过3个轮次的内外流耦合迭代计算后，防冰腔内外表面各参数分布逐渐趋于收敛。其中，由于干空气条件下第1轮次为初场计算，防冰腔外表面温度设置为定壁温，因此图12中并未给出该轮次下的温度分布，但增加了第4轮次内流与固体域计算结果。对比耦合迭代的第3轮次和第4轮次防冰腔外表面温度分布可以看出，两者基本达到一致。

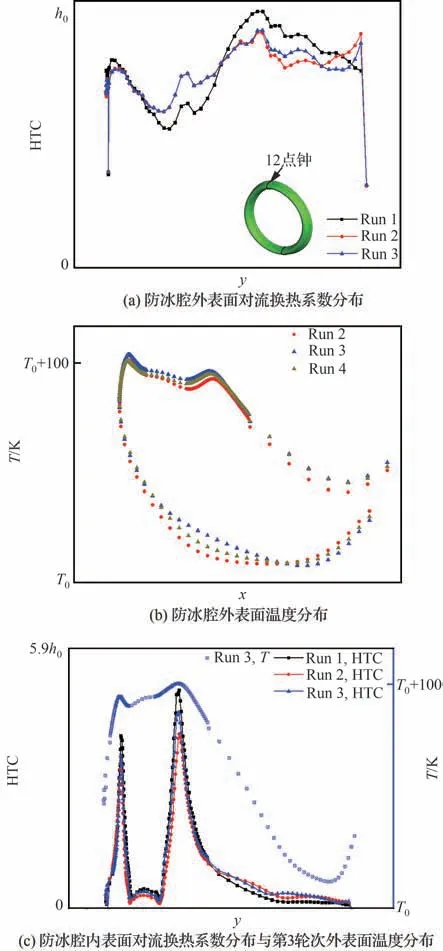
图14 干空气条件下短舱进气道防冰腔内外表面参数分布曲线（12点钟方向）Fig.14 Parameter distribution curves on internal and ex⁃ternal surfaces of nacelle inlet anti-icing chamber under dry air condition （12 o’clock direction）

如图14所示，取短舱进气道防冰腔在12点钟方向上的参数分布曲线，可以更加准确地分析干空气条件下内外流松散耦合迭代计算的收敛过程。可以看出，第1轮次防冰腔内外表面对流换热系数分布均与第2轮次计算结果有较为明显的差距，但第2轮次和第3轮次各参数分布曲线基本重合；第3、4轮次的表面温度曲线吻合良好，可达到迭代收敛要求；防冰腔内表面对流换热系数分布曲线在迭代过程中变化不大，仅射流驻点区域随迭代轮次略有下降。综上，干空气条件下防冰腔内、外表面平均对流换热系数在耦合迭代过程中均呈现先减后增再逼近收敛结果的变化规律，而防冰腔外表面平均温度则先增后减至迭代收敛。

3.3 水滴撞击特性

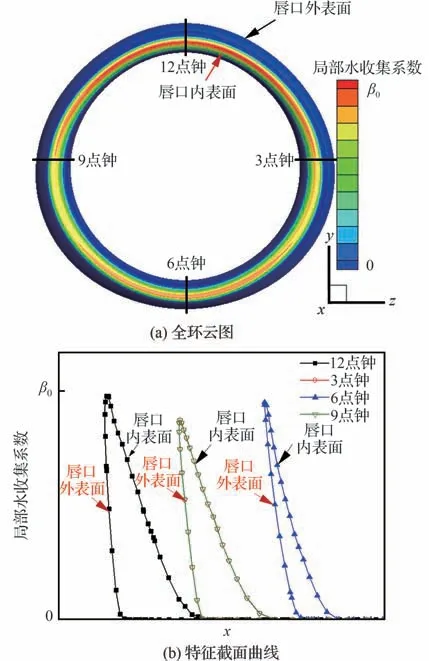
图15 短舱进气道防冰腔外表面局部水收集系数分布Fig.15 Local collection efficiency distributions on ex⁃ternal surface of nacelle inlet anti-icing chamber

图15为短舱进气道防冰腔外表面局部水收集系数分布，图中β0为局部水收集系数基准值。可以看出，水滴撞击区域主要集中在唇口前缘驻点位置附近，且唇口内表面撞击极限要明显大于唇口外表面，沿唇口周向各截面上局部水收集系数分布并不均匀，12点钟方向具有最大的局部水收集系数峰值和撞击范围，而6点钟方向撞击范围明显减小，3点钟和9点钟方向左右对称，具有相同的局部水收集系数分布。由于水滴撞击特性计算结果是后续防冰热分析计算的输入，唇口表面局部水收集系数的周向分布不均匀性很大程度上会影响湿空气条件下防冰腔表面的换热特性及温度分布。

3.4 湿空气防冰热分析

图16~图18为湿空气条件下短舱进气道笛形管防冰腔外表面等效换热系数、温度以及内表面对流换热系数在内外流松散耦合不同迭代轮次下的计算结果。相比于干空气条件，湿空气条件下耦合迭代轮次明显增加，这是由于该工况条件下表面撞击水量不能完全蒸发并在防冰腔表面形成周向不均匀分布的溢流水流动，如图19所示，其中m0为溢流水质量流量基准值。溢流水量分布与表面换热特性相互影响，导致表面温度分布收敛速度减缓。防冰腔外表面由于过冷水滴撞击引入的热质传递源项，湿空气条件下外表面等效换热系数要明显大于干空气条件；而对于防冰腔内表面对流换热系数，干、湿空气条件下数值变化并不大。此外，相较于干空气条件，湿空气条件下进气道防冰腔外表面温度明显下降，且表面温度均匀性有所提升。

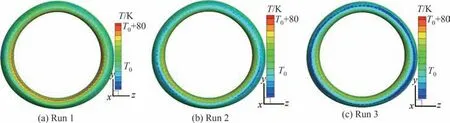
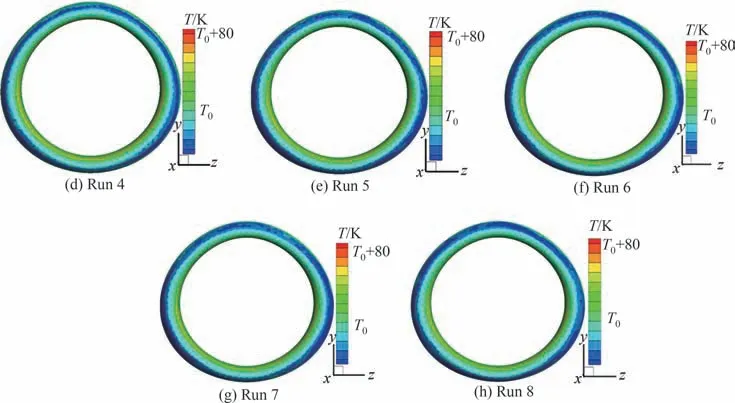
图17 湿空气条件下短舱进气道防冰腔外表面温度分布Fig.17 Temperature distributions on external surface of nacelle inlet anti-icing chamber under wet air condition

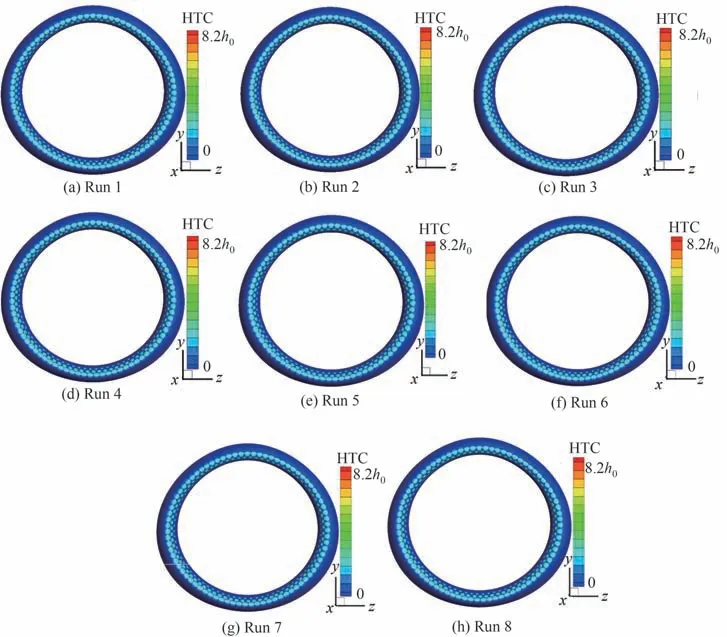
图18 湿空气条件下短舱进气道防冰腔内表面对流换热系数分布Fig.18 Convective heat transfer coefficient distributions on internal surface of nacelle inlet anti-icing chamber under wet air condition

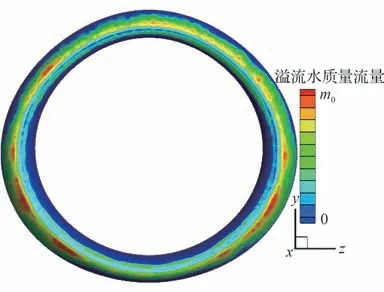
图19 湿空气条件下短舱进气道防冰腔外表面溢流水质量流量分布（第8轮次迭代）Fig.19 Runback mass flux on external surface of na⁃celle inlet anti-icing chamber under wet air con⁃dition （Run 8）

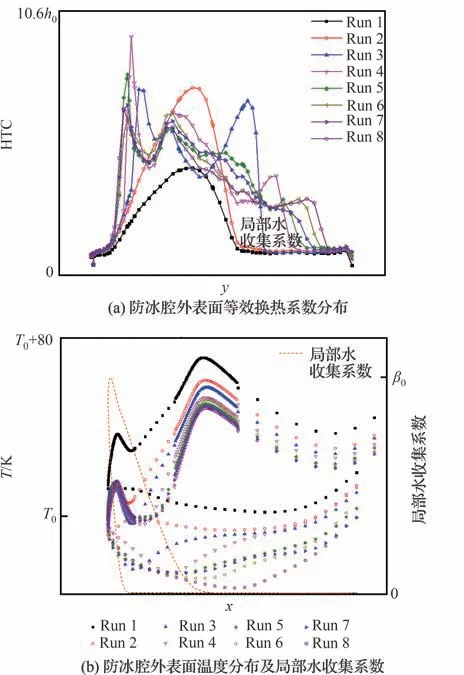
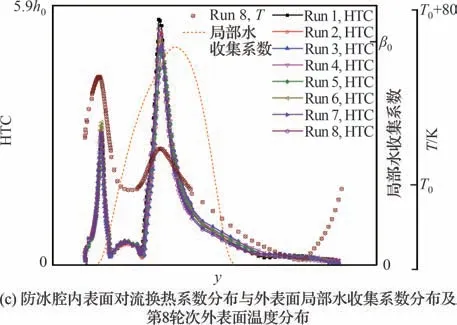
图20 湿空气条件下短舱进气道防冰腔内外表面参数分布曲线（12点钟方向）Fig.20 Parameter distributions curves on internal and external surfaces of nacelle inlet anti-icing chamber under wet air condition （12 o’clock direction）

结合图20所示的短舱进气道防冰腔内外表面各参数在12点钟方向上的分布曲线可以看出，在撞击区域内松散耦合迭代的第1轮次到第4轮次防冰腔外表面温度下降明显，且外表面等效换热系数分布也发生较大的变化，但从第5轮次开始到第8轮次计算结果都较为接近，尤其在唇口内表面各参数曲线吻合良好，但在唇口外表面撞击极限之后的蒙皮外表面等效换热系数及温度分布还略有差异。总的来说，湿空气条件下防冰腔内外表面参数在耦合迭代过程中所呈现的变化规律与干空气条件恰好相反。防冰腔外表面平均等效换热系数与内表面平均对流换热系数在迭代过程中均先增加后减小再逼近收敛，而防冰腔外表面平均温度则先降低后升高直至迭代收敛。