翼型结冰状态复杂分离流动数值模拟综述

赵宾宾，张恒，李杰

1．西北工业大学 航空学院，西安 710072

2．中国商用飞机有限责任公司 上海飞机设计研究院，上海 201210

3．清华大学 航天航空学院，北京 100084

结冰是民机飞行安全的主要威胁之一。翼面结冰状态下的气动特性评估是适航取证验证、结冰防护研究、容冰安全飞行的重要依据［1-2］。前缘复杂分离是翼型结冰状态气动特性影响研究的核心问题［3］。此时分离流场由剪切层失稳和多尺度旋涡运动支配，其本质是几何间断-压力梯度共同作用下的分离-再附过程，具备较强的非线性/非定常特征，将造成最大升力系数损失、失速迎角提前、抗扰动能力下降、进入失速状态的可能性大幅提高。相关流动机理的认识和总结仍然不尽完备，流动特性改变与气动力变化之间的关联性也并不明确。很大程度上对结冰致灾机理的深入研究构成了严重制约。

目前翼型结冰后流场和气动力的相关研究手段涵盖飞行试验、风洞试验和数值模拟。飞行试验可信程度较高，是确定结冰前后气动特性变化情况的重要依据；但存在耗费巨大、危险性高、流场信息相对匮乏的问题。风洞试验可在降低研究成本和风险的前提下，得到较为贴近实际的气动数据；但存在测量参数有限、数据相关性需要修正的问题。相对而言，数值模拟能够获取较为全面的流场信息，实现相对简捷和经济，能够与气动力设计分析流程紧密结合，是评估结冰影响、剖析流动机理的有效方法。

翼型前缘结冰导致的失速分离形态及机制与干净翼型大迎角状态存在本质差异。干净翼型失速分离特征一般与流向逆压梯度直接相关。而结冰翼型的分离生成通常是由于积冰当地几何特征发生突变，使得剪切层直接失稳脱落，剪切层涡系结构的发展促进了回流区域和主流区域的流动掺混效应，最终在下游与壁面相互作用、发生再附现象，形成湍流分离泡。因此，驱动分离流动的实质因素是几何间断触发Kelvin-Helmholtz（K-H）不稳定性和迎角效应产生压力梯度两者的综合效应，主导失速分离特征的核心是分离泡结构的生长、扩展和膨胀现象，这无疑大大增加了分离流动数值模拟分析的复杂度。

近年来，随着计算流体力学（Computational Fluid Dynamics， CFD）方法的不断进步，一系列新型数值模拟方法得到了发展，获得了许多有价值的结论和数据，为结冰状态下的飞行安全与防护研究提供了重要的理论储备与技术支撑。然而在Bragg［3］和Lynch［4］等知名学者发表的有关综述中，相对注重结冰后分离流动问题的物理机制探讨，而缺乏从数值模拟方法角度出发的总结性分析。虽然Stebbins等［5］于2019年业已完成了关于结冰翼面气动特性计算评估手段的综述性文章，但未针对湍流模拟方法的应用效果进行详细分析和评论。鉴于在描述分离流场结构及其演化特征层面的重要地位，仍然有必要进一步从湍流模拟方法的角度，针对结冰后气动特性预测及分离流场特征描述等方面的沿革进展进行评述；不仅为结冰影响分析手段的选取及应用提供参考依据，也为模拟方法的修正及完善提供评判准则。

本文首先对翼型结冰后数值模拟研究的基本框架进行介绍；在此基础上从典型湍流模拟方法的实际应用层面，回顾近年来数值方法在结冰翼型失速特性预测、分离流场特征刻画等方面的进展；最后对研究手段和研究内容的相关发展趋势进行总结和展望。

1 结冰分离流动模拟概述

由于冰生成过程相对非定常流场演化特征而言具备较大的时间尺度，在目前的翼型结冰分离流场数值模拟工作中，通常将结冰过程研究和流场分析研究解耦，采用结冰试验或数值模拟研究中某时刻获得的冰形建立几何模型。伴随几何重构技术的发展，大致经历了二维简化冰形—二维真实冰形—考虑三维效应的展向拉伸冰形—具备完全三维特征的真实冰形这一发展过程。得益于多块结构化网格、非结构混合网格和嵌套网格等技术的不断完善，目前已能够针对复杂结冰外形生成大规模贴体计算网格，为精细化数值模拟方法特别是新型湍流模拟方法的成功应用建立了良好的基础。

鉴于分离流动的高度复杂性和对气动特性的强烈影响，数值模拟中通常选取角状冰和冰脊作为典型冰形。图1［3］给出了翼型前缘角状冰诱导产生的瞬时流场结构示意图（图中α为迎角，U∞为来流速度）。图中显示在K-H不稳定性的驱动下，冰角顶端的剪切层失稳伴随复杂的多尺度旋涡脱落和输运过程，促进了外部高速流动与近壁面回流流动之间的混合，生成几何尺度较大的分离泡结构。在压力梯度的作用下，这种复杂流动结构通常在翼型失速点附近表现出较强的非定常特征，不仅使得分离泡的几何特征参数随时间变化，并且关于来流扰动变化的拉伸-膨胀效应及演化机制高度复杂，进而导致宏观气动力的高度不稳定，是当前翼型结冰状态分离流动数值模拟研究关注的重点内容。

图1 角状冰后方瞬时流场结构示意图［3］Fig.1 Schematic diagram of transient flow field struc⁃ture behind horn ice［3］

就气动特性分析而言，数值模拟研究重点关注结冰翼型失速迎角的确定、最大升力系数及失速形态的变化情况。显而易见地，翼型失速特性的准确预测依赖于把握上述前缘分离泡的生成演化过程，这对湍流模拟方法的精度提出了较高要求。随着雷诺平均（Reynolds Averaged Navier-Stokes， RANS）方法、大涡模拟（Large Eddy Simulation， LES）方 法 和RANS/LES混合方法的相继建立和完善，数值模拟对湍流流场的描述更加准确，获得的流动特征量更加丰富，能够更好地反映分离流动的非定常本质。以下从不同类型湍流模拟方法的应用角度，对近年来数值模拟研究的进展情况进行简要评述。

2 RANS方法

RANS方法将瞬时流动变量分解为平均量与脉动量两部分，使得方程中出现了额外的雷诺应力张量，从而需要引入某种假设对该变量进行估计。依靠对湍流内在演化机制的描述，能够对雷诺应力做出各种假设，建立附加方程模型从而刻画湍流平均量。对于翼型结冰后流动的计算分析，通常采用的湍流模型包括一方程Spalart-Allmaras（S-A）模型［6］、两方程k-ε模型［7］、k-ω模型［8］和Shear-Stress-Transport（SST）模型［9］等。采用的几何模型涵盖二维到三维，允许使用单元尺度较大的计算网格，相应的空间离散格式精度要求也较低，可基于定常或非定常方式进行流场求解，对计算资源的要求较易满足，因此在数值模拟研究的早期阶段及现阶段工程领域得到了广泛应用。

应用RANS分析翼型结冰后气动特性变化的工作始于20世纪80年代。Potapczuk和Gerhart［10］首先应用薄层RANS方法进行了一些基本的结冰 翼 型 气 动 特 性 计 算。Kwon和Sankar［11-12］对 翼型结冰引起的局部流动分离现象进行了数值模拟。Shim等［13］初步研究了冰形几何形状同翼型气动特性变化间的相关性，就不同湍流模型的效果进行了分析。Chi等［14-15］基于图2所示的二维结构网格，分别针对霜冰和明冰条件下的GLC305翼型进行了宏观气动力计算，就湍流模型对计算结果的影响进行了对比。对于图3（a）［14］给出的霜冰算例（图中CL为升力系数），不同湍流模型在升力线性段附近获得的结果基本类似，与试验吻合程度良好；但最大升力系数和失速迎角均与试验值存在一定差距。而对于图3（b）［14］给出的明冰翼型，湍流模型的影响扩展到升力线性段，失速点附近的计算结果差别较大，均无法较好地反映升力变化的基本特征。就该算例而言，SST等复杂湍流模型的效果并不明显优于S-A模型。图4［15］给出的明冰翼型流向速度（u/U∞）分布对比情况表明，S-A模型未能在失速临界迎角附近准确预测分离泡的基本形态，获得的再附位置较试验结果明显偏后，反映了常用湍流模型在刻画结冰诱导分离流动特征层面的固有缺陷。

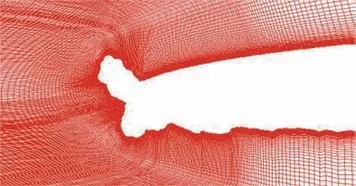
图2 明冰冰形附近二维结构网格［14］Fig.2 Two-dimensional structured grid near glaze ice shape［14］

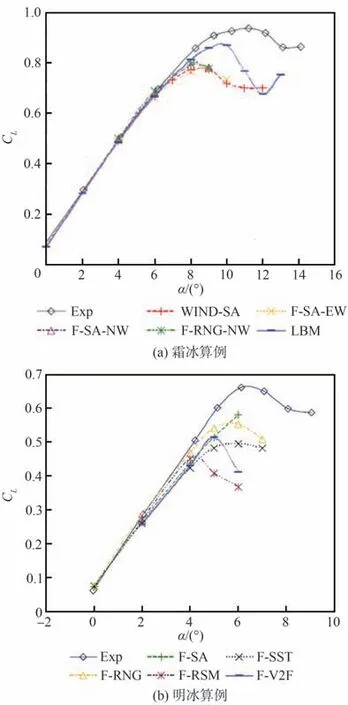
图3 翼型升力系数计算结果对比［14］Fig.3 Comparison of computed results of lift coeffi⁃cients for airfoil［14］

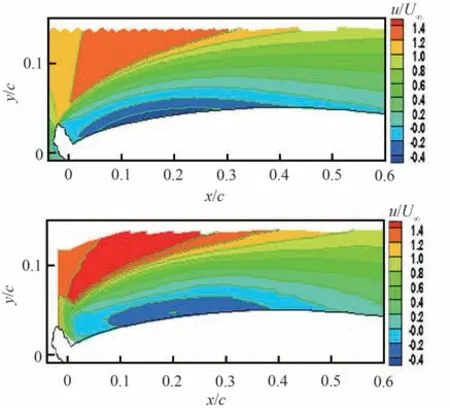
图4 明冰翼型流向速度分布对比（α=6°，上：S-A模型计算结果；下：试验结果）［15］Fig.4 Comparison of streamwise velocity contours of airfoil with glaze ice（α=6°，top： result of S-A model；bot⁃tom： result of test）［15］

Pan和Loth［16］就 简 化 冰 形 对 不 同 翼 型 气 动力造成的影响进行了较为系统的分析，归纳了来流马赫数和雷诺数效应，分析了冰形弦向位置与压力分布形态间的关联，同样表明小迎角状态下取得的数值结果基本可用，但同时也指出RANS在失速点附近无法准确计算气动力，特别对于几何尺寸较大的冰形而言，由于分离强度显著增加，数值结果与试验值间的差异不容忽视。

Marongiu等［17］针对层流翼型NLF0414结典型双角状明冰后的气动特性改变问题，在不同求解器的基础上对比了S-A模型和SST模型的模拟 效 果。图5（a）［17］给 出 的 结 果 表 明RANS在 小迎角下获得的压力分布情况均比较满意，但由于失速点附近的压力恢复过程和旋涡空间输运过程直接相关，图5（b）［17］所示的计算结果与试验值之间出现了较大偏差。该算例中SST模型在分离流动较强时取得的气动力预测结果优于S-A模型。此外，文献［17］还指出大迎角下即使采用非定常RANS也难以有效描述流动的分离特性，因此借助RANS/LES混合方法或LES方法等更为精细的湍流模拟方法进行流场求解是必要的。

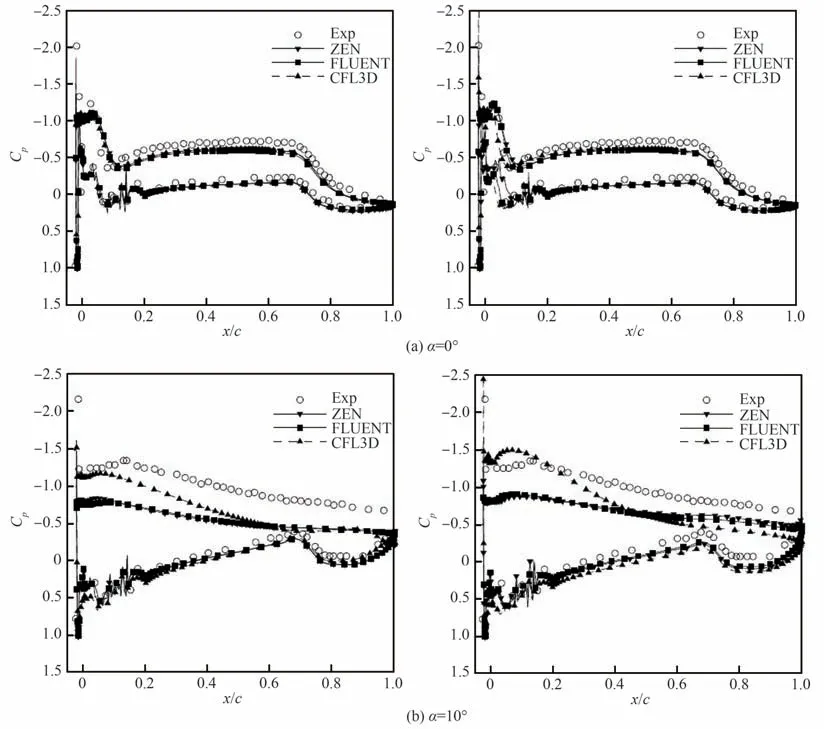
图5 压力系数Cp分布对比（左：S-A模型；右：SST模型）［17］Fig.5 Comparison of pressure coefficientCpdistributions （left： S-A model； right： SST model）［17］

Jun等［18］通 过 激 光 扫 描 技 术 建 立 了NACA 23012翼型前缘真实冰形的 三 维 数 模。图6［18］体现了非结构网格较强的几何外形适应性。基于RANS方法获得了物面压力分布和升力特性曲线等基本气动数据。图7［18］表明由于几何模型复杂度的提高，即使在小迎角下，压力分布的计算精度也并不十分满意。Mirzaei等［19］基于两方程k-ε模型分析了NLF0414翼型角状冰影响下的宏观分离流场演化过程，在中小迎角下获得了与试验结果吻合良好的再附位置/湍流强度极值等关键特征量。

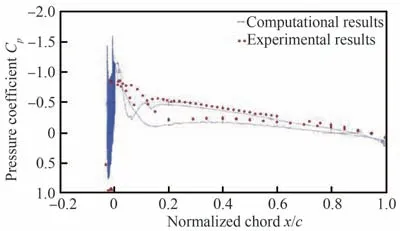
图7 α=0°时模型中面压力分布对比［18］Fig.7 Comparison of midspan pressure distributions of model atα=0°［18］

近年来国内研究者也相继开展了一些有代表性的研究工作。陈科等［20-21］基于近壁面非结构网格-远场结构化网格的思路，发展了一种混合网格生成方法，避免了复杂结冰外形难以划分结构化网格的问题；针对一类具备不规则前缘冰形的翼型，分别基于S-A模型和SST模型进行了气动特性计算分析，较好地预测了翼型失速点之前的升力特性变化情况。李焱鑫等［22］结合雷诺应力模型（Reynolds Stress Model， RSM）［23］，针对大型客机典型超临界翼型及平尾翼型带溢流冰条件下的气动力进行模拟分析，表明该模型可较为准确地预测结冰翼型的最大升力系数与失速迎角。Li等［24-25］在考虑湍流非平衡特性的前提下发展了2种分离修正湍流模型，有效提升了翼型结冰状态失速分离流场的预测精度。黄冉冉等［26］基于S-A模型量化分析了具备不同微观特征参数的冰形对翼型失速特性的影响规律。

以上结果表明，基于简化的结冰几何构型，在分离流动强度有限的小迎角及临界迎角条件下，RANS能够取得较好的宏观流场和气动力数值结果。因而在机理研究的初始阶段及工程应用领域，不失为一种能够有效描述分离流场概貌、高效获取气动数据的方法［27］。但是，由于结冰翼型失速点附近存在丰富的旋涡生成演化及相互作用，与湍流脉动相关的非定常效应占据主导地位；而RANS对脉动信息采用完全模化的处理方式，难以合理描述复杂流动细节，能够得到的流动特征量比较有限；并且对于不同计算条件和结冰外形，同一湍流模型的气动力预测准确程度也存在差别。因此，在结冰诱导分离流动的机理研究工作中，仍然有必要应用更为符合物理事实、精度更高的湍流模拟方法。

3 LES方法

LES认为湍动能由大尺度运动主导，难以基于普适性模型描述；耗散则由小尺度运动主导，且各向同性效应显著。因此对大尺度运动进行直接求解，而小尺度运动则采用模化处理，尺度划分通过流动变量在空间上的加权积分完成。这种处理方式使得方程中出现了亚格子应力张量，需要进行模化处理。在远离壁面的分离区域，LES能够有效给出湍流瞬时脉动信息，较为精确地描述流动细节特征。对于翼型结冰分离流动问题而言，该方法应用的计算模型一般为具备一定展向长度的准三维模型，要求计算网格在分离区域具备较高的各向同性性质且足够精细。同时还需要配合高精度空间离散格式，并以较小时间步长进行非定常推进，因而对计算资源的要求总体较高。

目前应用LES方法分析翼型结冰后分离流动的工作还比较有限。Brown等［28］应用Implicit LES（ILES）方法［29］，针对一类结冰旋翼翼型开展了数值模拟研究。在三维冰形的构建过程中应用 了 高 精 度CT扫 描 技 术，图8［28］显 示 该 冰 形 具备结构复杂、随机性较强和不规则度较高的特点。图9［28］以Q等值面［30］的形式给出了翼型不同迎角下的瞬时流场结构，表明ILES较为精细地描述了剪切层失稳和旋涡脱落过程随迎角的变化情况，有效地刻画了空间三维小尺度湍流结构。但图10［28］显示计算所得的翼型失速特性与试验值之间仍存在差距。表明仅仅增加湍流模拟方法复杂度并不能有效改善结冰翼型失速点附近气动力的预测结果。

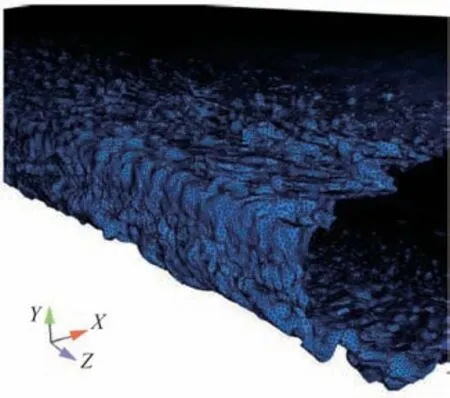
图8 三维冰形表面非结构网格［28］Fig.8 Unstructured surface mesh of three-dimensional ice shape［28］

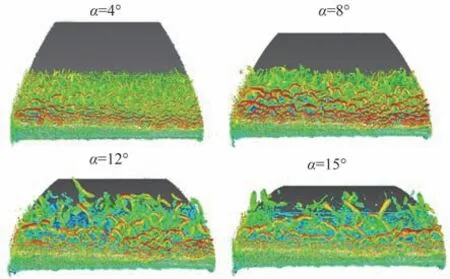
图9 不同迎角下瞬时流场Q等值面［28］Fig.9 Iso-surface ofQ-criterion of instantaneous flow structure of different angles of attack［28］

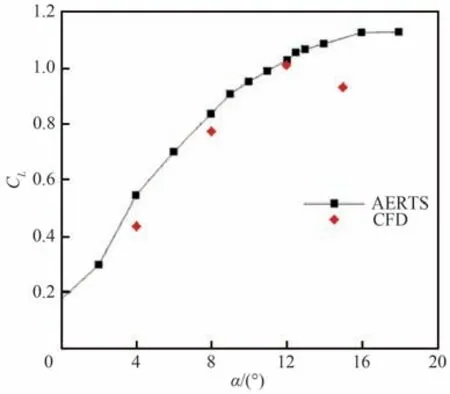
图10 升力特性曲线对比［28］Fig.10 Comparison of lift characteristic curves［28］

LES壁 面 模 型（Wall-Modelling in LES，WMLES）［31］在 非 常 靠 近 壁 面 的 边 界 层 内 体 现RANS特征，而在其余区域则体现经过修正的LES方法基本性质。Xiao M C等［32］结合中心-迎风混合格式，基于WMLES系统分析了GLC305及NLF0414翼型结冰状态下的分离演化规律，表明数值方法能够准确刻画自由剪切层的K-H不稳定性，在此基础上就分离流场的非定常频域特征进行了深入探讨。图11［32］给出了冰角后方剪切层失稳后二维涡管卷起生成三维大尺度类发卡涡的演化过程。但是，由于结冰分离流场中存在典型再附特征；就小尺度、高频率湍流结构主导的附着边界层流动而言，LES在近壁模型的构造和完善方面尚存在一些缺陷，附着区域的合理界定和判断、模化/解析区域的快速转换仍然是制约LES广泛应用的固有难题。因此，LES在翼型结冰分离流动分析中的推广仍有相当多的前置工作需要开展。

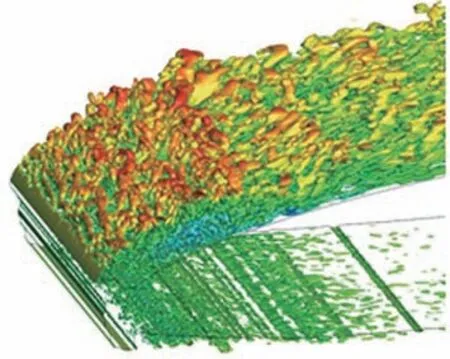
图11 NLF0414结冰翼型剪切层涡系结构［32］Fig.11 Vortex structures of shear layer of NLF0414 iced airfoil［32］

4 RANS/LES混合方法

由于RANS方法和LES方法对湍流附加应力项的描述能够以相似的形式给出；因此可以采取较为简洁的手段对两者加以混合。其基本思想是在壁面附近流动区域模化各向同性的小尺度湍流结构，体现RANS性质，在降低计算资源需求的同时，维持壁面附近流动信息的求解准确程度，避免雷诺应力损失；在远离壁面的分离区域则对大尺度旋涡进行解析，体现LES性质，保证分离区域湍流运动的模拟精度。该方法要求分离区域网格三向同性并且划分足够细密，但在近壁面可使用长宽比较大的薄层网格［33］。一般采用多块结构化网格或结构/非结构混合网格，以满足不同性质湍流模拟方法对网格布置的需求。对空间离散格式和非定常计算时间步长的要求较LES略低，所需的计算资源总体高于非定常RANS但低于LES［34］，并且易于程序实现，因而成为了近年来的研究热点，开始逐步应用于结冰后复杂分离流动的计算分析工作中。

一般根据构造形式将RANS/LES混合方法归纳为两大类，即湍流量混合法和混合界面法。湍流量混合法的基本思想是采用加权思想对RANS雷诺应力项和LES亚格子应力项进行混合；其重点是如何构建合理的加权混合函数。混合界面法将流场分为RANS区域和LES区域分别进行计算。令湍流模拟方法在部分流场区域（例如近壁面区域和远场区域）内体现RANS性质，而在其余流场区域（例如流动分离区域）内则体现LES性质。采用这种方法对流场进行数值模拟，则在2个流动区域之间必然存在分界面。该方法的重点是对分界面进行合理界定，并保持分界面两侧流动变量的光滑过渡［35］。

混合界面法中具备代表性的一类方法是Spalart等［36］于1997年 提 出 的 分 离 涡 模 拟 方 法（Detached Eddy Simulation， DES/DES97）。该方法将S-A湍流模型和LES亚格子应力模型结合为统一模型，通过比较当地网格尺度与湍流混合长度进行方法转换。在近壁面区域表现为传统RANS方法；在以大涡输运为主要特征的区域快速降低当地雷诺应力水平，体现LES方法的特点，解析求解大尺度空间湍流结构。但采用该方法会出现模化应力损失（Modeled Stress Depletion，MSD）［37］问题，引起网格诱导分离（Grid Induced Separation， GIS）。造成这种现象的主要原因是壁面附近区域的网格单元各向尺度大致相当时，DES97方法会将此区域标定为LES区域，此时壁面边界层内雷诺应力模化不足，计算过程中边界层内涡黏性将会过度减少。为了解决MSD问题，Menter和Kuntz［38］通 过 引入SST湍流模型中 的 过渡函数，实现了壁面边界层到主流区域的渐进转换。Spalart等［37］基于相似的思想，采用“延迟LES函数”使LES亚格子应力模型推迟进入壁面边界层区域，此类方法称为延迟DES方法（Delayed DES， DDES）。通 过 将DDES与WMLES相 结合，Shur等［39］提出了IDDES方法。IDDES对亚格子尺度进行了重新定义，并且在同时考虑RANS和LES长度尺度影响的前提下构造了RANS/LES混合长度，一定程度上解决了DES类方法直接应用于WMLES时产生的“对数层不匹配”（Log-Layer Mismatch，LLM）问题。

Pan和Loth［40-41］较 早 地 利 用DES方 法 对 带简化冰脊模型的NACA23012翼型绕流进行了分析，冰形附近的多块结构网格如图12［41］所示。结果表明在失速点附近，DES获得的宏观气动力结果较RANS方法有所提升。图13［41］显示DES计算所得的压力恢复过程明显优于RANS；但由于分离区域计算网格量较为有限，只获得了图14［41］所示的旋涡结构概貌，但初步显示了DES解析空间分离区域大尺度湍流特征的能力。

图12 简化冰形附近多块结构网格［41］Fig.12 Multi-block structured grid near simplified ice shape［41］

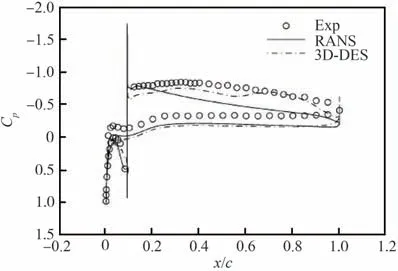
图13 压力分布对比（α=5°）［41］Fig.13 Comparison of predicted pressure distributions（α=5°）［41］

图14 瞬时流场展向涡量分布云图［41］Fig.14 Contours of spanwise vorticity of instantaneous flow field［41］

Thompson［42］和Mogili［43］等 基 于 非 结 构 混 合网格，利用DES对GLC305翼型结角状冰后不同迎角下的流场和气动力变化问题做了较为全面的分析研究。提出了将冰角高度与关注区域单元尺度相互关联的网格设计思路，就数值方法的网格敏感性开展了系统的对比分析，基准网格和加密网 格 空 间 分 布 对 比 情 况 如 图15［42］所 示。图16［42］和图17［42］给出的失速点附近压力和速度分布计算结果表明，由于DES有效描述了剪切层涡系演化过程的时间累积效应，因此不仅能够较为准确地描述压力分布的平台特征及其恢复过程，同时能够更好地预测时均分离泡的再附位置和其几何形态。图18［42］给出的湍流强度分布情况也与风洞试验结果基本类似，表明DES在分离区域能够有效切换到LES模式，充分解析湍流脉动信息。

图15 冰形附近混合网格［42］Fig.15 Hybrid mesh near ice shape［42］

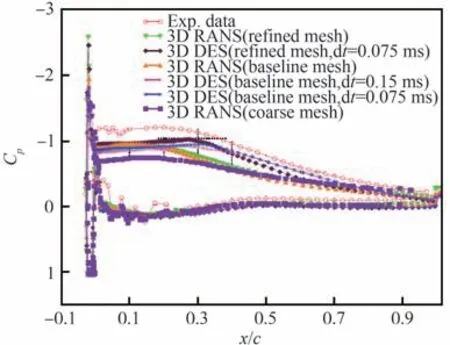
图16 压力分布对比（α=6°）［42］Fig.16 Comparison of predicted pressure distributions（α=6°）［42］

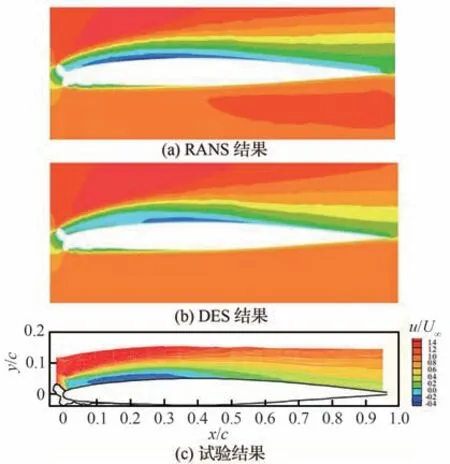
图17 时均流向速度分布对比（α=6°）［42］Fig.17 Comparison of time-averaged streamwise ve⁃locity distributions（α=6°）［42］

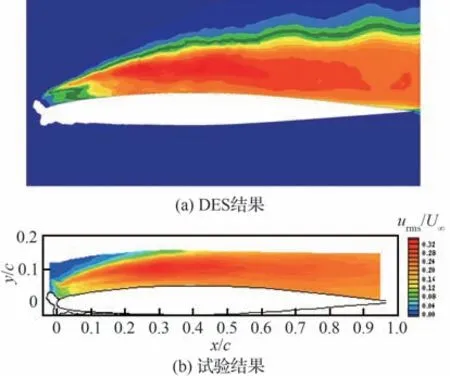
图18 流向速度脉动均方根对比（α=6°）［42］Fig.18 Comparison of root-mean-square of fluctuations in streamwise velocity component （α=6°）［42］

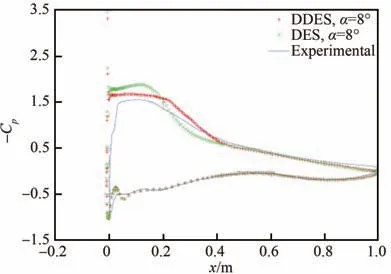
图19 时均压力分布结果对比（α=8°）［44］Fig.19 Comparison of time-averaged pressure distribu⁃tions （α=8°）［44］

Lorenzo等［44］分 别 采 取DES和DDES就 平尾翼型M5-6结冰失速前后的气动力变化情况进行了分析，认为失速点之前的宏观气动力计算结果是比较满意的。图19［44］表明在临界失速条件下，DDES较DES能够更为准确地反映结冰翼型的时均压力分布平台特征，集中体现于描述了更为和缓而非相对急促的压力恢复过程，对应更加符合物理事实、更为靠近下游的旋涡结构生成及掺混现象；其主要原因是DDES通过引入延迟函数，避免了LES亚格子尺度过度侵入RANS区，从而减缓了原始DES存在的模化应力衰减、K-H不稳定性过度释放问题。Lakshmipathy和To⁃giti［45］对 比 了PANS （Partially Averaged Navier-Stokes）［46］方 法 和DDES方 法 对NACA23012翼型结冰后强分离流动的模拟效果，图20［45］和图21［45］表明DDES能够提供更好的时均压力分布结果，同时能够更为充分地解析尾迹区域的三维湍 流 结构。Alam等［47-48］在GLC305翼型 临 界失速状态算例中也在一定程度上肯定了DDES的流场细节刻画能力。Molina等［49］采用DDES和非结构网格开展了基于SU2程序的GLC305结冰翼型临界失速分离流场分析研究，肯定了引入自适应亚格子尺度对预测结果的改善作用。

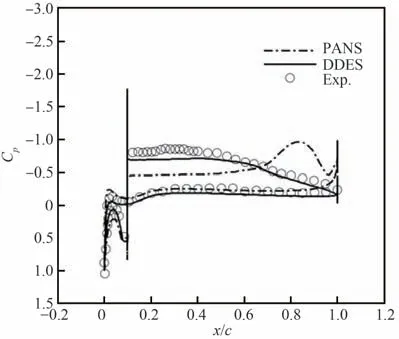
图20 时均压力分布结果对比［45］Fig.20 Comparison of time-averaged pressure distributions［45］

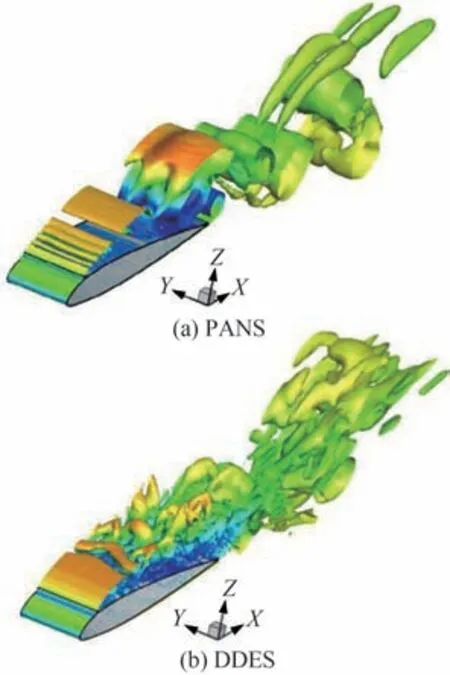
图21 瞬时流场Q等值面对比［45］Fig.21 Comparison of iso-surface ofQ-criterion of in⁃stantaneous flow field［45］

但是，上述研究工作中同时也指出DES类方法对结冰翼型失速后强分离流场的预测精度仍存在一定提升空间。其中的首要问题是冰角后方RANS/LES区域的延迟转换特征与剪切层失稳过程解析需求的高度不匹配，由此生成的强亚格子黏性严重制约了K-H不稳定性的合理释放，预测得到的三维旋涡结构生成位置通常较试验结果更为接近下游，使得剪切层摆动-失稳、二维涡管释放-扭曲、发卡涡结构发展变化等典型剪切层相关精细湍流特征难以得到充分辨识，制约了分离流动机理特别是非定常特征的深入剖析。

近年来，IDDES方法逐渐成为了结冰分离特征精细预测的重要手段。国内Xiao Z X等［50-52］率先基于该方法开展了一系列卓有成效的研究工作，表明该方法在强分离区域具备与DDES相当的湍流模拟精度，同时在附着和分离并存的过渡区域能够取得更为满意的计算结果，因此适用于分析剪切层分离-再附效应主导的结冰失速分离问题。在该方法的基础上，翼型结冰后分离流场的研究范畴得到了进一步拓展，不仅包含传统意义上的临界失速分离泡模拟分析，并且涵盖了失速点后分离泡的膨胀机制、剪切层失稳相关的非定常模态特征等领域，国内在该领域积累了较为丰富的研究经验：张恒等［53-54］采用该方法分析了GLC305结冰翼型失速阶段分离泡的拉伸-膨胀历程，指出发卡涡抬升导致剪切层涡系掺混融合作用降低是驱动结冰翼型失速分离流场演化的关键机制；Hu等［55-56］厘清了角冰/冰脊诱导剪切层的失稳及旋涡脱落模式，初步建立了流场关键模态与不同尺度旋涡之间的关联；Bao等［57］将该方法延拓到结冰翼型气动噪声特性的分析研究工作当中；谭雪等［58-59］基于该方法进一步识别了冰脊触发分离的各阶模态特征，表明大尺度旋涡结构是导致翼型临界失速状态升力波动的根本原因。

由 于 传 统DES方 法 通 常 采 用Δ=max(Δx，Δy，Δz)（Δx、Δy、Δz分别为x、y、z向的计算网格间距），即Δmax作为亚格子模型。当计算网格严格各向同性时，该亚格子尺度等同于经典LES尺度，即1/3网格单元体积的立方根。但对于以近壁区域为代表的典型各向异性网格而言，平行物面方向单元尺度一般远大于法向单元尺度，显然上述定义将会导致当地长度尺度过大，造成当地涡黏特征过度预测，降低了DES类方法对湍流精细结构的解析能力。针对上述问题，Shur等［60］提出了一种综合考虑计算网格当地几何特征与湍流流场信息的亚格子模型，利用湍流流场信息指示准二维流动特征，能够较为合理地降低各向异性网格/准二维分离区域的亚格子黏性，同时在各向同性网格/充分发展的三维分离区域恢复传统LES亚格子模型的特征。国内Xiao M C和Zhang［61］结 合 不 同 亚 格 子 应 力 模 型［62］分 析 了GLC305及NLF0414翼型角冰/冰脊影响下的翼型失速分离流场，基于IDDES-SLA［60］方法精细刻画了剪切层涡结构的生成演化模式及空间压力脉动规律，如图22~图24所示。由于SLA（Shear Layer Adapted）模型的基本思路为在各向异性较大的网格处采用各个网格节点位置加权处理的亚格子尺度与相关流场信息相乘的新亚格子尺度，因此具备在各向异性较强、剪切作用显著的流动区域有效降低当地涡黏性、提高K-H不稳定性解析能力的特点，从而增强了冰角后方剪切层失稳过程的刻画精度。因此，亚格子模型或亚格子常数的合理修正及完善同样是结冰翼型分离流场模拟方法改进阶段值得关注的重点研究内容之一。

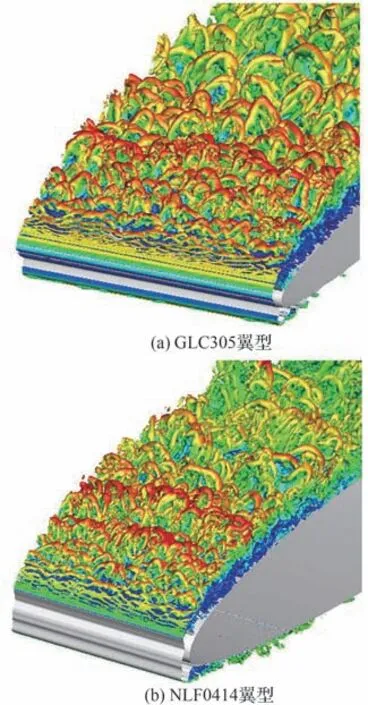
图22 IDDES-SLA方法捕获的多尺度旋涡结构［61］Fig.22 Muti-scale vortices structure captured by IDDESSLA［61］

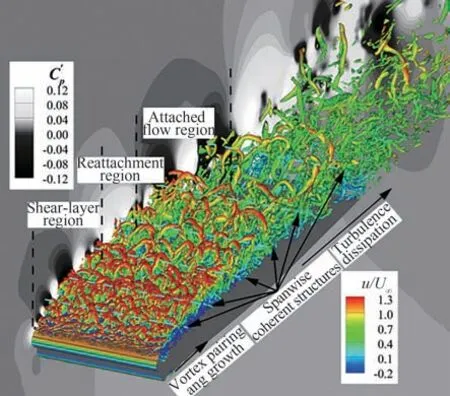
图23 IDDES-SLA刻画的剪切层涡系结构生成演化规律［61］Fig.23 Generation and evolution of shear layer vortex structure described by IDDES-SLA［61］

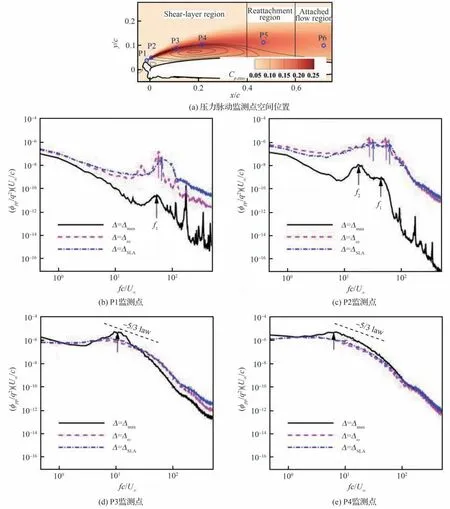
图24 不同亚格子模型捕获的空间压力脉动特征［61］Fig.24 Characteristics of spatial pressure fluctuations captured by different subgrid models［61］

Zonal DES（ZDES）方法是另一类有代表性的RANS/LES混合方法。该方法根据分离流场的基本结构，在基准DES方法［28］的基础上，以区域交界面的形式将流场人为划分为RANS区域和DES区域，实现湍流模拟方法的混合［63］。Duclercq等［64］基 于 图25所 示 的 多 块 结 构 化 网 格，利 用ZDES方法对展向冰脊诱导产生流场的非定常脉动特征进行了较为细致的研究。由于该方法能够在冰角后方人为强制切换到LES模式，因而具备相对较好的K-H不稳定性预测能力。由图26［64］可知数值方法能够较为准确地预测分离泡的涡核位置和时均速度分布情况。通过在冰脊后方剪切层脱落处设置如图27（a）［64］所示的2个监测点，给出了如图27（b）［64］所示的邻近冰角当地速度脉动功率谱密度（PSD）。图中给出的特征频率f0表征了剪切层内部旋涡的脱落频率；而特征频率f1可视为剪切层垂直运动的基频。图28［64］以Q等值面的形式显示了冰脊后方的瞬时流场，表明ZDES对分离区域小尺度三维湍流结构具备较强的解析能力。

图25 冰脊附近多块结构化空间网格［64］Fig.25 Muti-block structured grid near ice ridge［64］

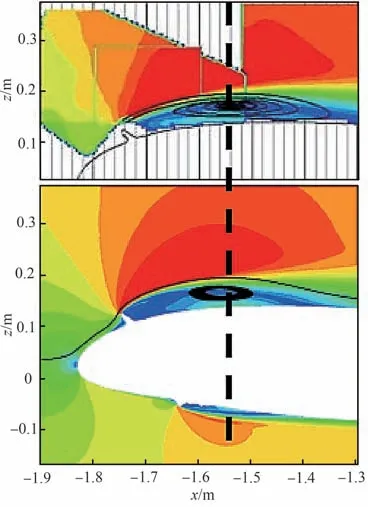
图26 时均流向速度分布对比（上：PIV试验结果；下：ZDES计算结果）［64］Fig.26 Comparison of time-averaged streamwise ve⁃locity contours （top： result of PIV； bottom： re⁃sult of ZDES）［64］

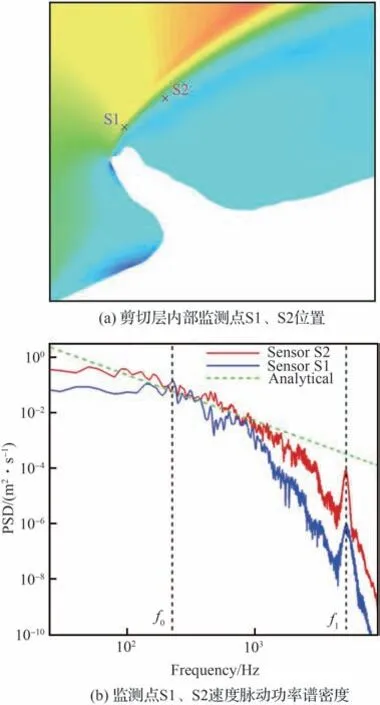
图27 冰脊后方流动速度脉动功率谱密度［64］Fig.27 Power spectral densities of velocity fluctuations behind ice ridge［64］

Deck［63］通过对长度尺度项进行修正，实现了ZDES的 改 进。Zhang等［65］基 于 该 方 法 分 析 了GLC305和NACA23012两类翼型不同结冰条件下的分离流动，指出计算域展向长度的选取将影响尾迹区域湍流结构的精确解析。由图29［65-66］可知，在展向长度增加到与分离泡长度接近的情况下，尾迹区域获得的大尺度旋涡基本形状和小尺度湍流结构精细程度明显高于展向长度较小的算例。Costes等［66-67］应用嵌套网格对类似的结冰分离流动算例进行分析时，认为ZDES表现出了较强的网格敏感性，影响流动再附位置的判定和旋涡脱落过程的解析；这与RANS区域和DES区域的空间划分位置、网格密度差异都有着密切联系。

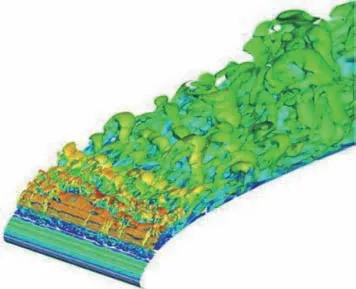
图28 Q等值面显示的冰脊后方瞬时流场［64］Fig.28 Iso-surface ofQ-criterion of instantaneous flow field behind ice ridge［64］

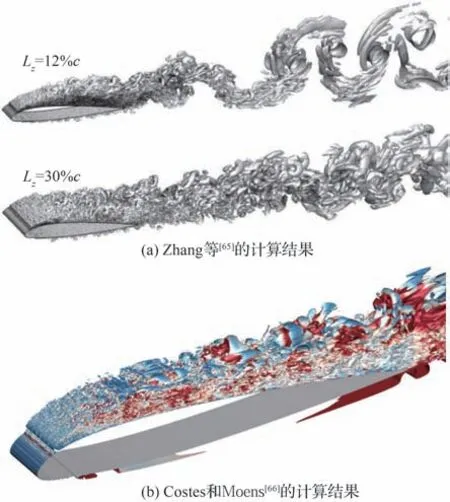
图29 ZDES方法获得的瞬时流场Fig.29 Instantaneous wake flow field of ZDES

Bhushan等［68-69］基于附加应力项加权混合的思路发展了一种动态RANS/LES混合模型（Dy⁃namic Hybrid RANS-LES model， DHRL），Alam等［47-48］基于该方法在非结构网格的基础上针对GLC305结冰翼型临界失速算例进行数值模拟，从近壁面速度分布和湍流脉动强度等流场细节角度验证了数值方法的可靠性。由图30［48］和图31［48］给出的粗细2套网格计算结果对比情况可知，由于该方法对RANS方法和LES方法的混合方式与当地网格参数并不直接相关，而是根据当地湍流信息直接判定，因此该混合模型对网格布置的依赖性相对较小，能够在网格整体较为稀疏的情况下，给出较DDES更为良好的近壁流动细节预测结果。图32［48］给出的流向速度等值面表明该方法对瞬时流场结构的描述也是较为精细的，能够较DDES更早地预测到因剪切层失稳导致的旋涡析出和运动现象。但该方法的计算效率目前尚不十分满意，相同推进步数下耗费的计算时间较DDES方法高出15%左右。

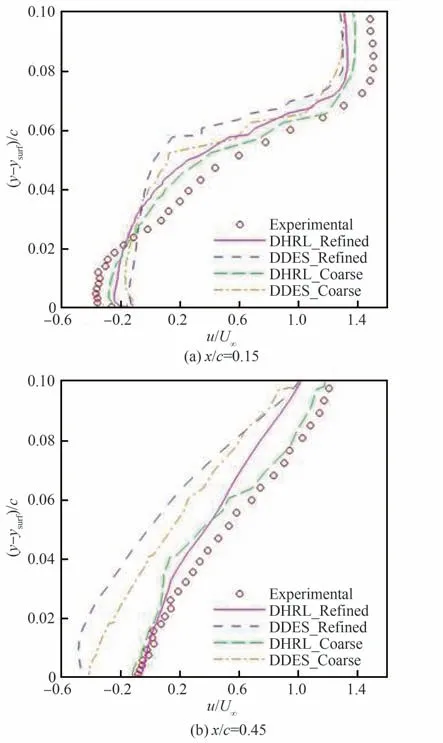
图30 壁面附近平均流向速度型对比［48］Fig.30 Comparison of mean streamwise velocity pro⁃files near wall［48］

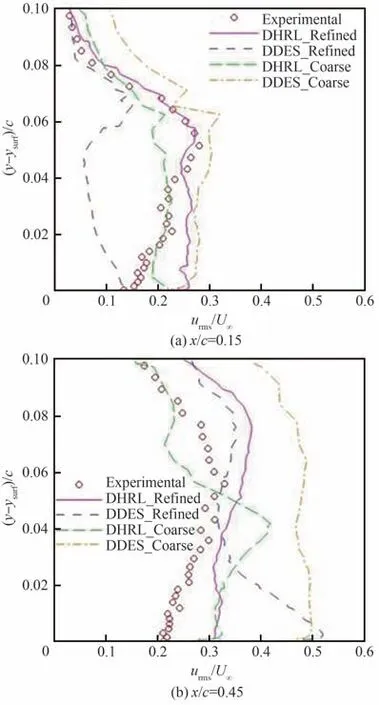
图31 壁面附近流向速度脉动均方根对比［48］Fig.31 Comparison of root-mean-square of fluctuations in streamwise velocity component near wall［48］

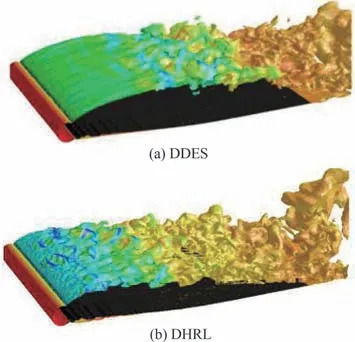
图32 瞬时流向速度等值面［48］Fig.32 Iso-surface of instantaneous streamwise velocity［48］

综上所述，就结冰后翼型分离流动的精细化数值模拟而言，现阶段RANS/LES混合方法能够较为准确地预测失速分离流动的基本形态和多尺度结构的演化过程，并对流场速度分布细节和湍流脉动情况进行合理描述。然而，目前此类方法在结冰分离流动问题研究中所涉及的结冰几何外形和流动状态还比较有限，不同混合模型的适用性仍有待验证，特别是国内外近年来提出的一些新 型RANS/LES混 合 方 法，例 如PANS［70］、SAS［71］、CLES［72］、窗 口 嵌 入 式RANS/LES［73］等仍有待在该领域加以推广应用。此外，冰角后方剪切层区域LES模式的快速合理转换仍然是需要解决的首要问题；从分离-再附流动的结构完整性出发，目前开展的大多数工作主要关注数值方法在分离起始阶段的表现，但对于与再附过程密切关联的多尺度旋涡结构-近壁面流动相互干扰现象预测效能仍然有待针对性改进，从而进一步提升再附位置的精准捕捉及压力恢复过程的合理描述能力，同时为剪切层-再附点摆动运动模式的深入分析提供更为可靠的方法手段［74-75］。

5 结束语

综上所述，现阶段关于翼型结冰后复杂分离流动的数值模拟研究取得了长足进步，前缘分离泡演化过程的刻画精度不断提高，给出的流场特征量更加准确和全面；所关注的问题从定常状态下的基本气动力和流场结构等宏观问题延拓到非定常涡脱落和湍流脉动机制等细节特征。但是，由于结冰诱导分离流动与生俱来的影响因素高度复杂、物理问题尺度差异巨大、多学科深度交叉融合等特征，相关工作仍然有待进一步开展，尤其在复杂冰形构造、湍流模拟方法的发展及应用、流动非定常特性等方面还需要深入研究。从而更为完备和清晰地认识翼型结冰状态复杂分离流动演化蕴含的深层次物理机制，更为准确和快捷地提供气动性能特别是失速特性的预测结果，以期更好地为民机适航取证验证、飞机结冰致灾机理及飞行安全防护研究提供支撑，具体包括以下几个方面：

1）考虑随机性的高精度冰形模型构造研究。由于现阶段冰形测量、提取及重构手段的限制，当前研究通常采用二维几何轮廓沿展向拉伸的冰形构造方式。但是，实际飞行过程自然生成的翼面结冰并不满足上述连续光滑过渡条件，而是具备显著的展向非规则、不连续及粗糙度等特征。上述因素导致的剪切层不稳定性改变/类射流涡系结构生成等特殊现象无疑增加了数值模拟分析研究的复杂度。如何在数值模拟分析研究中如实反映上述精细特征，不仅需要进一步完善物面复杂几何边界计算网格的生成策略，并且对湍流模拟方法特别是RANS/LES混合方法及WMLES方法的近壁面模型构造提出了更高要求，期望长度尺度具备更为灵敏的切换能力以及更为良好的复杂几何边界适应性。

2）新型湍流模拟方法的构造和应用研究。对于结冰翼型失速点附近分离流动演化过程的精准模拟和分析而言，目前所应用的湍流模拟方法仍然是不尽完备的，关于压力梯度驱动下K-H不稳定性的捕捉精度及旋涡-壁面相互作用现象的辨识能力仍然在很大程度上与冰形-翼型几何特征直接相关，同时依赖于冰角后方计算网格密度的提升及拓扑结构的人为设计。因此，就RANS/LES混合方法而言，期望K-H不稳定性的解析降低对于冰角后方区域当地计算网格设计及布置的严格要求、RANS/LES模式的转换更为全面地考虑当地流场物理机制及湍流信息而非仅注重边界几何特征因素；从而更为精确地识别冰角触发剪切层多尺度涡系结构的失稳—卷起—壮大—输运这一完整物理过程，同时更为合理地描述再附过程完成之后的边界层特征。此外，RANS/LES方法与自适应网格的有机结合也是可供参考借鉴的解决途径之一。

3）结冰后分离流动的深层次非定常特性研究。虽然现阶段数值模拟研究能够获得不同时刻瞬态流场的丰富信息，但对功率谱密度/模态特征等统计学方法量化的时域/频域量研究涉及不多。需要更为深入地结合本征正交分解（Proper Orthogonal Decomposition， POD）或动力学模态分解（Dynamic Mode Decomposition， DMD）等方法，从时间维度上更为精细地辨识和提取深层次非定常因素，以期更为全面地剖析结冰状态下多尺度涡系结构生成演化过程的时空相关规律，更好地发挥RANS/LES混合方法和LES方法对分离区域湍流脉动描述较为准确的优势。

4）结冰过程-流动特性的实时耦合分析研究。由于真实飞行条件下结冰对翼型流动的影响必然属于时变过程，因而基于实时耦合的分析研究更能体现结冰生成的随机性质，能够反映由于冰层累积和增长导致的非定常特性，数值模拟结果具备更高的科学意义及实用价值。然而，由于结冰过程与分离流动两者涉及的研究领域跨度相对较大，属于典型的多学科交叉耦合问题，目前较为全面和系统的研究工作尚不多见。