基于密度峰值聚类和无参数滤波器的自训练方法
2023-01-31孙彩锋
孙 彩 锋
(山西大同大学物理与电子科学学院 山西 大同 037009)
0 引 言
半监督学习由于可以通过同时利用未标记数据和标记数据来进行数据样本改进,降低了对数据样本的要求,在诸多领域得到了广泛的应用[1-2]。而在半监督学习分类器发展过程中,自训练方法也以其简单、高效和自适应等特点被认为是最具代表性的方法之一,因此得到了学界广泛的讨论和研究[3-4]。
在自我训练方法中,错误标注是一个非常普遍、棘手甚至不可避免的问题[5]。一般情况下,自训练方法将误标记样本视为噪声实例,严重扭曲了数据的分布,降低半监督学习的泛化能力。因此,提出了一系列基于局部噪声滤波器的自训练算法,其中,剪辑自训练(self-training with editing,SETRED)和邻域自训练(self-training nearest neighbor rule using cut edges,SNNRCE)使用切边权值统计(cut edge weight statistic,CEWS)来滤除噪声实例[6-7],多标签剪辑自训练(multi-label self-training with editing,MLSTE)则使用剪辑最近邻(edited nearest neighbor,ENN)来滤除噪声实例[8-9]。随后,Triguero等发现,在自我训练方法中使用的大多数现有噪声滤波器的局部方法没有很好地执行,特别是当标记数据不足时,即大多数自训练方法中使用的局部噪声滤波器需要更多的标记数据才能工作[10]。另外,自训练方法中的局部噪声滤波器主要是k近邻(k-nearest neighbors,KNN)分类器,因此,该方法滤波能力很大程度上依赖于参数k[11]。除此之外,现有的局部噪声滤波器都是基于监督学习的,因此,它们并不完全与半监督学习兼容,因为它们只考虑标记数据的信息。
针对上述问题,提出了一种基于密度峰值和无参数局部噪声滤波器自训练方法。设计的一种新的无参数局部噪声滤波器,既能利用标记数据,又能利用未标记数据去除噪声。
1 理论方法
1.1 基于密度峰值的自训练方法

(1)
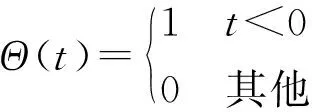
(2)
(3)
式中:ρ={ρ1,ρ2,…,ρn}是记录X中所有样本的局部密度的集合,即ρi是样本xi的局部密度,δ={δ1,δ2,…,δn}记录每个样本在X中的最小距离,即δi是样本xi与具有更高局部密度的任何其他样本之间的最小距离,通过计算ρi和δi,每个样本xi都有一个对应的样本xj,它是xi最接近的具有更高局部密度ρi的样本,dij是样本xi和xj之间的距离。这里采用欧氏距离,dc是具有预设值的截止距离。然后,使每个样本xi指向其对应的唯一样本xj。
在揭示特征空间的结构之后,STDP使用密度峰值聚类揭示的基础结构来帮助训练给定的分类器,定义L={x1,x2,…,xl}是X中所有标记样本的集合,U={xl+1,xl+2,…,xn}是X中所有未标记样本的集合。在该分类器中,未标记样本被连续标记并添加到L中。该标记过程分为两个步骤。第一步是从U迭代地选择L样本的所有“下一个”点并进行标记。第二步是从U迭代地选择L样本的所有“上一个”点并进行标记。
1.2 自然邻域
自然邻域是没有参数的邻域,主要想法来自对社交网络的理解[13]。一个人拥有的真正朋友的数量应该是将他或她视为朋友并同时被他或她视为朋友的人数。如果每个人至少都有一个朋友,则在社交网络中将形成一个相对稳定的结构,称为自然稳定结构(natural stable structure,NSS)。
定义1自然稳定结构:如果x将z视为邻域并且z同时将x视为邻域,则对象z是对象x的自然邻域。如果每个对象都有至少一个自然邻域,则数据集已形成一个相对稳定的状态,称为自然稳定结构[13]。
(∀xi)(∃xj)(r∈n)∨(xi≠xj)→
(xi∈NNr(xj))∨(xj∈NNr(xi))
(4)
式中:NNr(x)={x1,x2,…,xr}是包含样本x的r个最近邻域的集合。在式(4)中,搜索回合r从1增加到λ(λ≤n),λ是自然邻域特征值。当r=λ时,NSS在给定的数据集中形成。实际上,数据的复杂性可以用λ表示。值较小的λ表示数据规则或数据大小较小,而值较大的λ表示数据大小较大。此外,λ已经被用来解决参数k的问题。根据上面的描述,数据对象的自然邻域可以表述为:
定义2自然邻域(Natural Neighbor,NaN):xi的自然邻域定义如下[14]:
xj∈NaN(xi)⟺xi∈NNλ(xj)&&xj∈NNλ(xi)
(5)
式中:NaN(x)={x1,x2,…}是包含样本x的自然邻居的集合。算法1描述了自然邻域搜索算法。
算法1自然邻域搜索算法
输入:X
输出:NaN,λ
1.r=1,∀xi∈X,Nb(xi)=∅,NNk(xi)=∅,RNNk(xi)=∅,NaN(xi)=∅;
2.从数据集X中创造一个k-d树T
3.for数据集X的每一个xi通过T找到它的第r个邻域xj
4.NNk(xi)=NNk(xi)∪{xj};
5.Nb(xj)=Nb(xj)+1;
6.RNNk(xj)=RNNk(xj)∪{xi};
7.end for
8.计算num
9.ifnum没变
10.则λ=r;
11.for数据集X的每一个xi
12.NaN(xi)=RNNλ(xi)∩NNλ{xi};
13.end for
14.返回NaN,λ;
15.else
16.r=r+1;
17.回到第三步;
18.end if
算法1返回NaN和λ。Nb={t1,t2,…,tn}是记录数字的集合,式中ti(i=1,2,…,n)是被视为与其他样本相邻的样本xi的数目。另外,Nb(xi)记录被视为与其他样本相邻的样本xi的数量。在第2-7行中,计算NaN直到形成自然稳定结构。算法中增加了一个限制,即变量num不会更改,因为噪声会影响算法1。num是Nb(xi)==0的样本xi的数量,式中Nb(xi)表示被视为其他样本的邻域样本xi的数量。通常,时间复杂度为O(nlogn),因为在第2行中使用了k-d树。k-d树是划分k维数据空间的数据结构。它主要应用于多维空间中关键数据的搜索。
2 提出的算法
2.1 特征空间的结构揭示
图1显示了基于密度峰值和无参数局部噪声滤波器自训练方法(self-training method based on density peaks and an local noise filter,STDPNF)的一般框架,该框架由三部分组成。第一步中,使用密度峰值聚类发现特征空间的基础结构。然后,将此结构转换为所有样本的标记顺序。第二步是一个标准的自训练过程,根据标记顺序预测未标记样本并将其添加到中。此外,扩展的自然邻域剪辑滤波器(extended natural neighbor editing,ENaNE)可以删除噪声实例。第三步用扩展的重新训练KNN分类器。此后,可以更好地克服标记错误的问题,并且可以训练分类器。

图1 STDPNF的框架
在此将重新设计密度峰值聚类在STDP中显示的结构,以使其有利于结合提出的局部噪声滤波器。STDP存在标记错误的问题。因此,打算使用局部噪声滤波器来去除STDP中标记错误的样本。但是,一旦将错误预测的样本作为噪声实例丢弃,与丢弃的样本关联的几个未标记样本将没有机会被标记。图2给出了一个例子来说明这种情况。

(a) 揭示特征空间的结构

(b) 错误标记示意图图2 标记示例
在图2(a)中,密度峰值聚类揭示了特征空间的结构,其中每个样本都指向具有更高局部密度的相应最近样本。如图2(b)所示,样本x1被错误地预测。如图2(a)所示,样本x1应属于类1。如果样本x1作为噪声实例被丢弃,则样本x1将不会添加到L中。根据STDP的标记过程,一些样本例如样本x2和x3,将没有机会被标记。实际上,这种情况破坏了密度峰值聚类发现的结构。
为了在不影响密度峰值聚类发现的结构的情况下过滤出噪声实例,深入分析了密度峰值聚类在STDP中的作用。实际上,密度峰值聚类揭示的结构的功能是在STDP中提供带有标记顺序的未标记样本。因此,重新设计了密度峰值聚类揭示的结构。同时通过密度峰值聚类而不是X之间的连接关系的结构来获取所有样本的标记顺序。详细算法描述如下:
算法2结构揭示算法(DS)
输入:dc,L,U。
输出:order。
1.X=[L;U],count=1,order=∅;
2.arrows=密度峰值聚类算法(X,dc);
3.for数据集X的每一个xi
4.order(i)=0;
5.end;
6.重复上述步骤,直到从U中选择所有L样本的“下一个”点;
7.if未标记样本xi是L样本的“下一个”点
8.order(i)=count,L=L∪xi,U=U-xi;
9.end if
10.count=count+1;
11.重复上述步骤,直到从U中选择所有L的样本点;
12.if未标记样本xi是L样本的“前一个”点
13.order(xi)=count,L=L∪xi,U=U-xi;
14.end if;
15.count=count+1;
算法2返回变量order,该变量记录X中所有样本的标记顺序。例如,如果样本xi在第一次迭代中被标记,则order(xi)=1。此策略避免了图2中描述的问题。详细地说,第1行是初始化变量,第2行是运行密度峰值聚类。密度峰值聚类的算法返回arrows。如果样本xi指向样本xj,则arrows(i)=j。第3-第5行将初始化order。第6-第15行将根据arrows中隐含的结构和STDP的标记过程来计算order。算法2的时间复杂度为O(n2),因为算法2中最耗时的步骤是时间复杂度为O(n2)的第2行。
图3显示了算法2的示例,其中每个样本旁边都有一个数字。这些数字表示何时标记了相应的样本,通过算法2获得的结构更加清晰和易于理解。其中max(order)表示STDPNF中的最大迭代次数,另外每个样本在初始L中的order为0,因为它们不需要预测。

图3 算法2揭示的样本标记序列
2.2 扩展的无参数局部噪声滤波器
ENaNE是一个局部噪声滤波器,用于删除噪声实例,由于NaN是无参数的,使用NaN(x)表示样本x的局部邻域[15]。为了量化样本x及其局部邻域之间的差异,定义了样本x的负面影响度和正面影响度。
定义3x的负面影响度:样本x的负面影响度可定义如下,表示样本对于分类作用的负面影响程度。
Harmfulness(x)=|{z|z∈NaN(x) and label(z)≠label(x)}|
(6)
定义4x的正面影响度:样本x的正面影响度可以定义如下,表示样本对于分类作用的正面影响程度。
Usefulness(x)=|{z|z∈NaN(x) and label(z)==label(x)}|
(7)
式中:label(x)是返回样本x的类标签的函数。在定义3和定义4中,|·|表示集合的元素编号。例如,|{y|y∈
NaN(x) andl(z)≠l(x)}|表示集合{z|z∈NaN(x) andl(z)≠l(x)}的元素编号。已知样本x的正面影响度是实例z的数量,式中NaN(x)包含z且z的标签与样本x的标签相同。相比之下,样本x的有害性是实例z的数量,式中NaN(x)包含z且z的标签与样本x的标签不同。如果一个样本x是一个噪声实例,它的类标签与其在一个局部邻域即NaN(x)中的大多数周围样本不同,那么它的负面影响度自然大于它的正面影响度。
定义5噪声实例:如果样本x是一个噪声实例,它应该满足以下条件:
Harmfulness(x)>Usefulness(x)
(8)
根据定义5,可以滤除噪声实例而无需任何其他参数,因为NaN是无参数的。但是在半监督学习中,L通常非常稀缺,而U丰富且易于使用。当计算给定样本的正面影响度和负面影响度时,大量样本都没有被标记。因此,使用一种自训练方法来预测这些未标记的样本,这些样本将用于计算给定样本的正面影响度和负面影响度。
算法3返回没有噪声实例的剪辑集。ENaNE也可以删除异常值,因为异常值的NaN数通常为0,如第2行所示。在第3行中,将使用自训练方法来预测这些未标记样本,该方法将用于计算给定样本的正面影响度和负面影响度,其中未标记样本的预测顺序是基于变量order的。第4-第6行用于过滤噪声实例。本文中ENaNE中使用的自训练方法的基分类器是KNN,其中k=λ由算法1计算。λ已经被用来解决实例约简、聚类和离群值检测中选择参数k的问题。
算法3扩展的自然邻域剪辑算法(ENaNE)
输入:滤波样本,order,NaN,λ。
输出:剪辑的数据集ES。
1.ES=∅;
2.for所有滤波样本的每一个xi
3.计算给定样本的正面影响度和负面影响度,其中未标记样本的预测顺序是基于变量order,然后使用自训练方法来预测这些未标记样本;
4.ifHarmfulness(x)>Usefulness(x);
5.ES=ES∪xi;
6.end if
7.end for
结果显示,ENaNE克服了参数依赖性的问题,原因如下:(1) 局部邻域没有参数;(2) NaNs和λ在算法1中自动计算,而order在算法2中自动计算。此外,ENaNE更适合半监督学习,因为它可以利用标记和未标记的数据。图4显示了算法3的过滤过程的示例。图4(a)显示了数据的分布,其中每个样本都具有由密度峰值聚类显示的相应标记顺序。在图4(b)中,当标记样本x1时,运行算法3来确定样本x1是否为噪声实例。首先,发现NaN(x1)包含样本x2和x3,其中样本x2和x3未标记,并分别被绿色矩形包围。接下来,使用具有KNN(k=λ)分类器的自训练方法,根据样本x2和x3对应的标记顺序来预测这两个样本。如果正确预测了样本x2和x3,则将通过ENaNE将x1作为噪声实例删除。

(a) 数据的分布
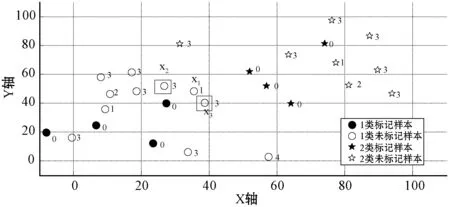
(b) 过滤结果图4 描述算法3的过滤过程示例
2.3 提出的自训练方法
算法4给出了本文提出的自训练方法。在第1行中,找到所有样本的标记顺序。在第2行中,搜索自然邻域。在第3-第10行中,通过连续标记未标记的样本、滤除噪声实例并更新L和U来迭代训练给定的KNN分类器C。最终,可以在第13行训练所需的分类器C并输出。
算法4SDTPNF
输入:dc,L,U。
输出:训练的KNN分类器C。
1.order=DS(L,U,dc);
2.[NaN,λ]=NaN_Search(L∪U);
3.通过L训练KNN分类器C;
4.count=1;
5.重复上述步骤,直到count>max;
6.从U中选择数据集TS,其中order=count;
7.用分类器C标记样本TS;
8.Filter_TS=ENaNE(TS,order,NaN,λ);
9.更新标记数据集L;
10.更新未标记数据集U;
11.通过L再次训练分类器C;
12.count=count+1;
13.通过L再次训练分类器C;
3 实验与结果分析
3.1 数据集和实验设置
本文使用具有8 GB内存、Core i7 CPU和64位操作系统的PC进行实验,以验证本节中提出的算法的效率。另外,使用MATLAB2015编写所有算法的代码。从加州大学欧文分校存储库中选择了18个实验基准数据集。表1中列出了数据集的描述。在所有实验中,均使用10倍交叉验证策略来确定ACC和STD的最终实验结果。
(9)
(10)
(11)

表1 数据集描述
训练集占了所有数据的90%,测试集占10%。在训练集中,使用随机分层选择将训练集分为标记部分L和未标记部分U。总共进行4个实验以验证所提出算法。简要说明如下:
(1) 实验一是将该算法与现有的代表性工作进行比较,其中L的比率为10%。
(2) 实验二是通过将其与现有代表性的局部噪声滤波器,其中L的比率为10%,通过比较,来验证提出的STDPNF中使用的局部噪声滤波器的优势。
(3) 在实验三中,讨论了L的比率的影响,其中将L的百分比从10%增加到90%。
(4) 在实验四中,比较了仅执行10次的所有代表性算法的运行时间。同样,L的比例为10%。
在所有的实验中,都把KNN作为基分类器,因为在KNN中通常使用局部噪声滤波器来去除噪声实例。
3.2 实验结果对比分析
实验一:自训练算法比较。选择的代表性算法如表2所示,其中比较算法的参数按建议设置。请注意,所提出的算法STDPNF具有参数dc。此外,每种算法的解释如下:
(1) 文献[6]提出了SETRED,它结合了CEWS以自训练方法过滤掉噪声实例。
(2) 文献[8]提出了MLSTE,其中ENN用于通过自训练方法滤除噪声实例。尽管提出将MLSTE应用于多标签任务,但也可以将其应用于单标签任务。
(3) 文献[16]提出了采用半监督模糊C均值自训练(self-training with semi-supervised fuzzy C means,STSFCM),其中使用模糊C均值聚类指导自训练方法来训练有效的分类器。
(4) 文献[17]提出了STDP。STDP可以训练有效的分类器,将密度峰值聚类揭示的特征空间结构集成到自训练过程中以训练有效的分类器。

表2 比较算法和参数
表3和图5显示了实验结果。表3显示,与比较算法相比,STDPNF通常可以训练更好的KNN。另外提出的算法3中获得了18个数据集中的15个的最高ACC。此外,表3中所有数据集上STDPNF的平均ACC也是最高的。在ILPD的数据集上,STDPNF的ACC低于STDP。可能的原因是ENaNE中的自训练方法会错误地预测未标记样本的类标签,从而削弱了ENaNE的能力。但是,在大多数数据集中,STDPNF的ACC都高于STDP,这表明STDPNF可以使用ENaNE有效地去除具有错误预测的样本。图5是所有数据集的ACC直方图,表明STDPNF明显达到了最佳ACC。综上所述,STDPNF在改善KNN性能方面比现有工作表现更好,并且可以有效去除标记错误样本。
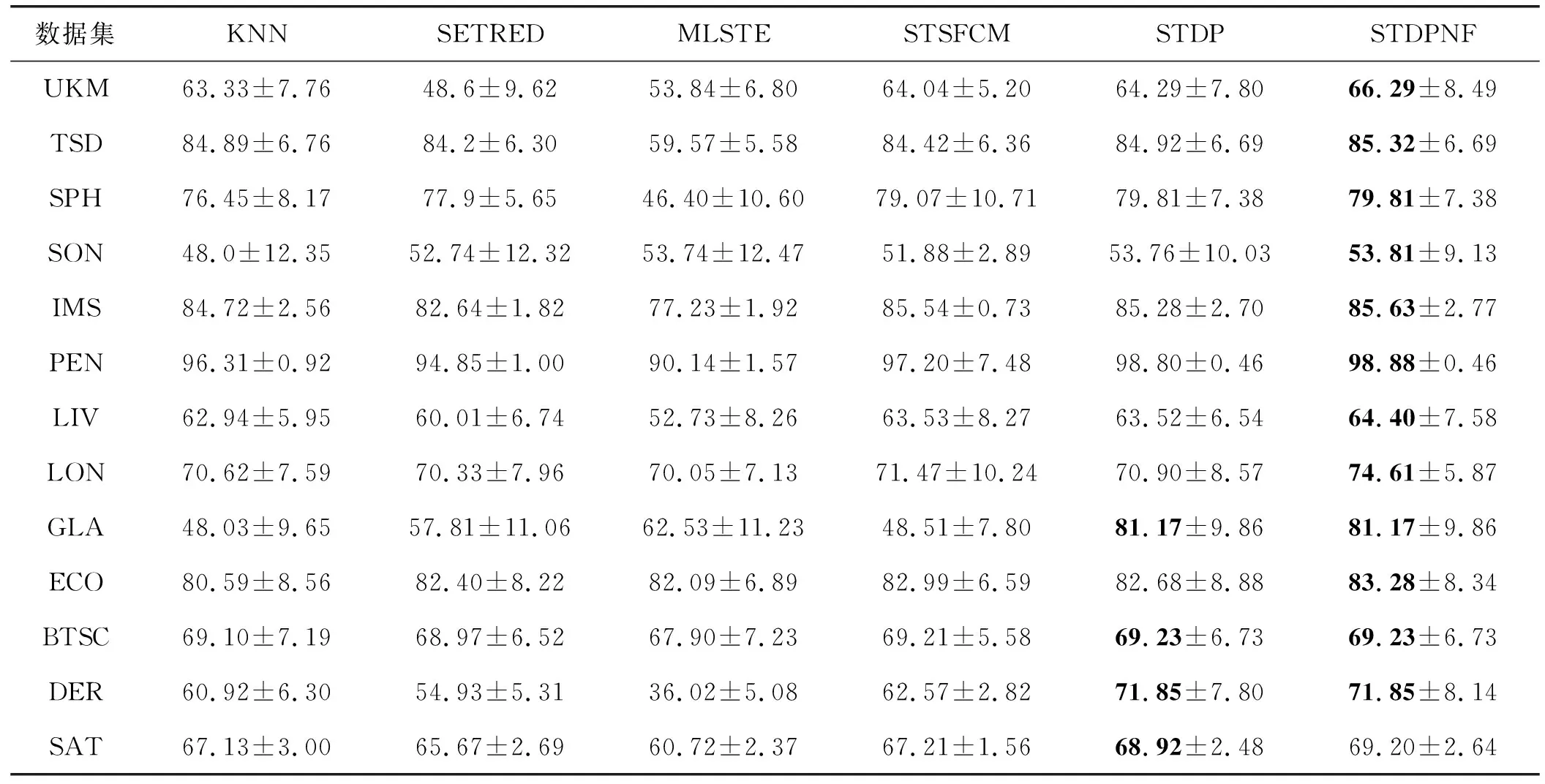
表3 分类准确率实验结果(%)
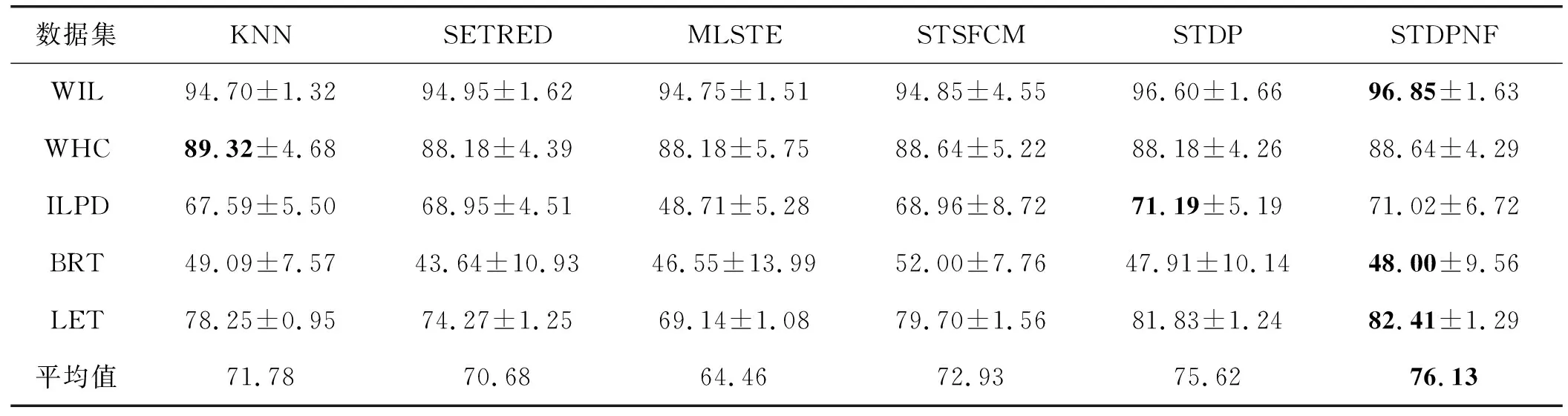
续表3
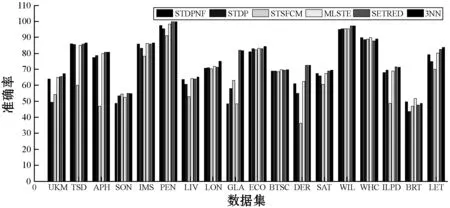
图5 18个UCI数据集的准确性直方图
实验二:局部噪声滤波器的比较。为了比较,选择5个代表性的局部噪声滤波器,例如ENN[8]、规则剪辑近邻(edited nearest-neighbor rule,RENN)[18]、自适应K近邻(adaptive K nearest-neighbor,AKNN)[19]、多标签剪辑近邻(multi-labled edited nearest-neighbor,MENN)[20]和CEWS。上述滤波器已被应用于自训练方法,以解决标记错误问题。然后,分别使用这5个代表性的局部噪声滤波器来消除STDP中的噪声实例(STDP_ENN、STDP_RENN、STDP_AKNN、STDP_MENN和STDP_CEWS)。表4给出了这些比较算法及其参数。
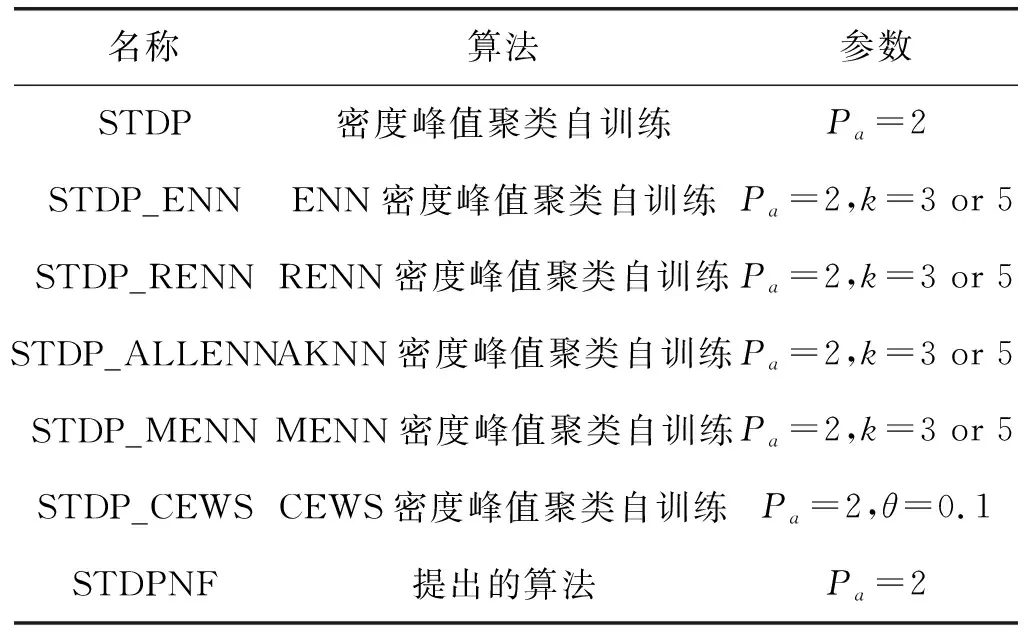
表4 滤波器比较算法和参数
根据相关文献令所有比较算法中的Pa=2。同样,将所有比较算法中的参数设置与先前使用一致。表5和表6给出了一些实验结果,以验证STDPNF中使用的ENaNE的优越性。表5中的ENN、RENN、AKNN和MENN的k为3,而表6中的ENN、RENN、AKNN和MENN的k为5。
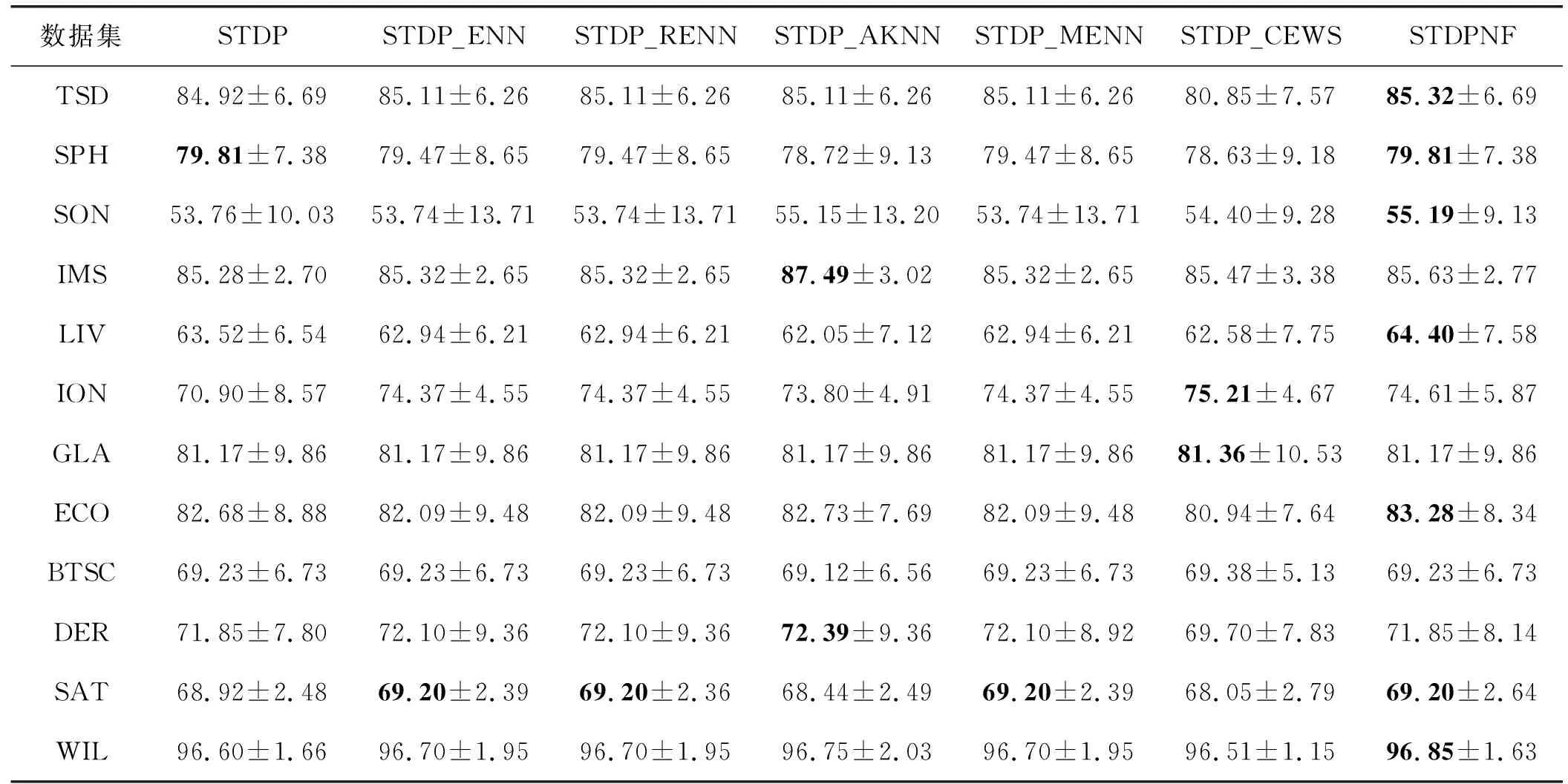
表5 STDP结合局部噪声滤波器的比较结果(ACC和STD,k=3)(%)

续表5
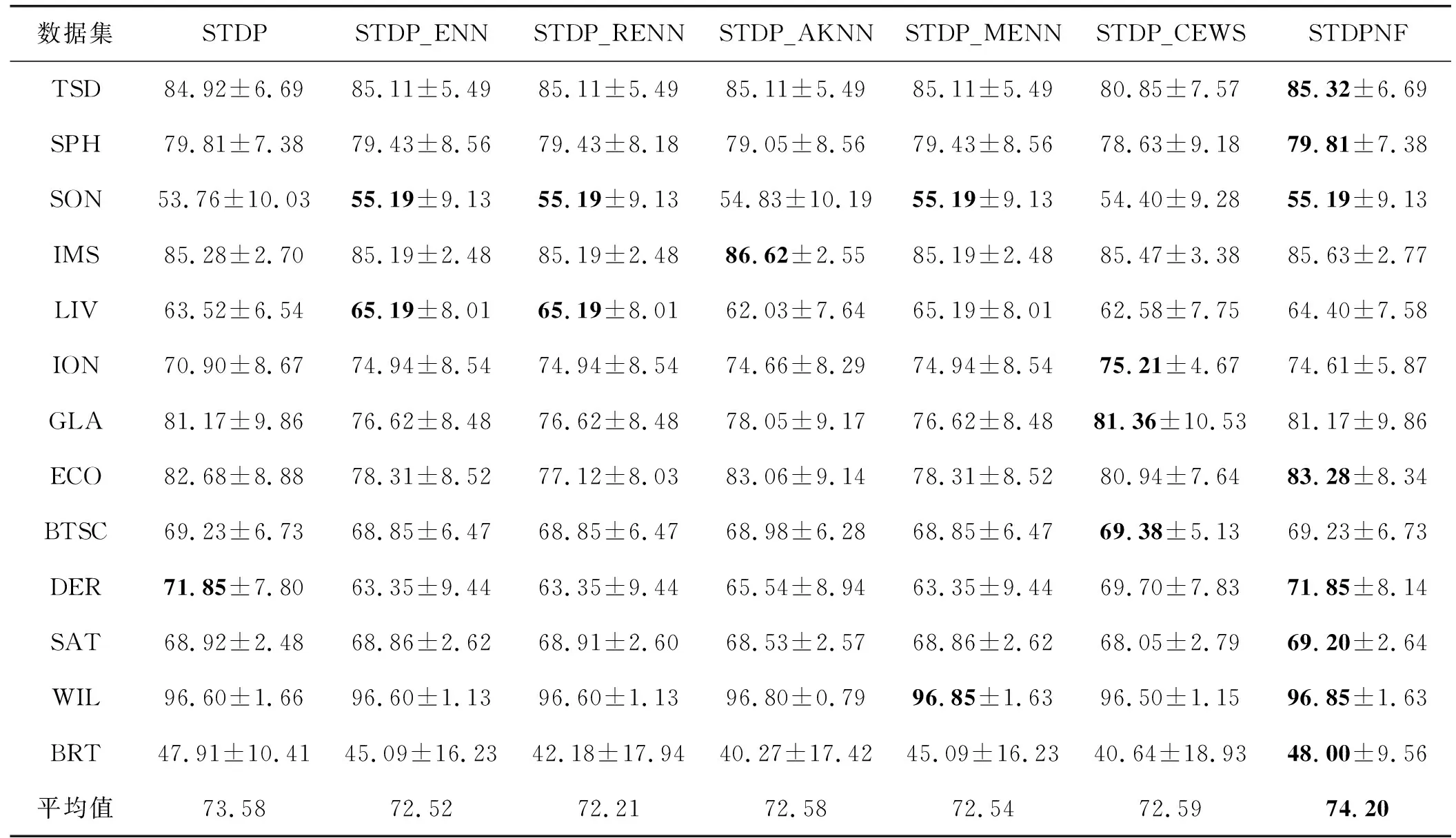
表6 STDP结合局部噪声滤波器的比较结果(ACC和STD,k=5)(%)
从表5和表6中可以看出,STDPNF实现了最佳性能。所提出的算法在表5和表6中的13个数据集中有8个达到了最高的ACC。STDPNF中所有数据集的平均ACC也是最高的。此外,可以发现,STDP中所有数据集的平均ACC均高于STDP_ENN、STDP_RENN、STDP_AKNN、STDP_MENN和STDP_CEWS。原因可能是另外5个代表性的局部噪声滤波器仅通过利用L的信息来滤除噪声,因此使得跟踪准确率不高。综合结果可知,这5个代表性的局部噪声滤波器可以滤除STDP中具有正确预测的样本。与5个代表性的局部噪声滤波器相比,ENaNE可以通过利用L和U的信息来滤除噪声实例。因此,STDPNF获得最佳结果。此外,ENaNE是无参数的。所有这些证据证明,所提出算法中使用的ENaNE优于自训练方法中使用的现有局部噪声滤波器。
实验三:标记样本比例的影响。本节将进一步讨论实验中不同比例L的影响。同时,选择STSFCM、STDP、STDP_ENN和STDP_AKNN作为比较算法,因为它们在实验一和实验二中的性能相对较高。STDP_ENN和STDP_AKNN中的局部噪声滤波器的k为3。图6显示了关于6个数据集上L的不同百分比的不同算法的ACC。
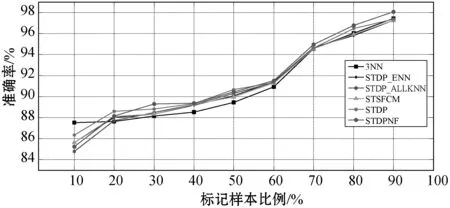
(a) 数据集:IMS
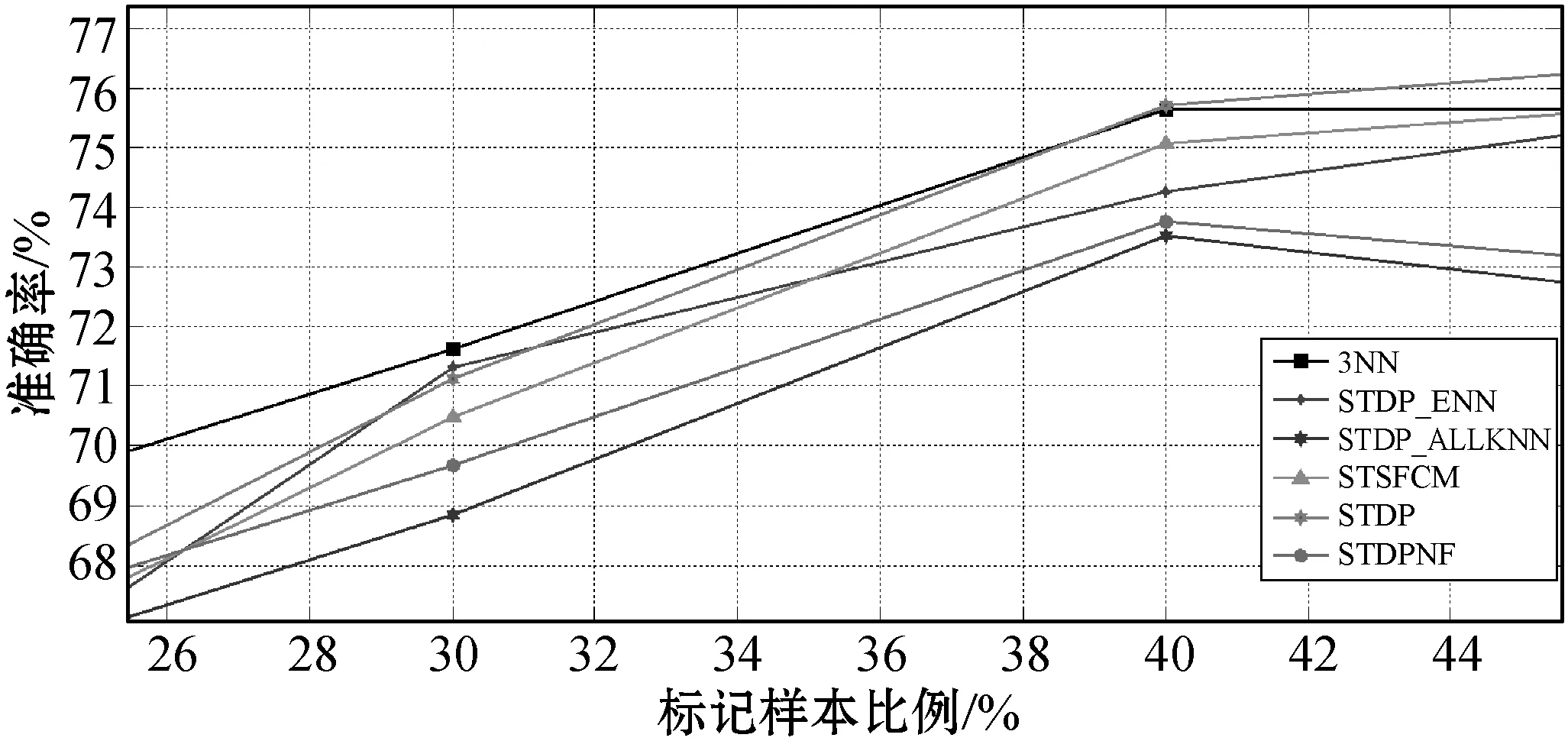
(b) 数据集:LIV
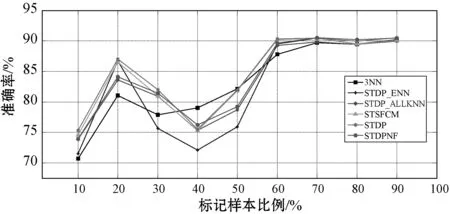
(c) 数据集:ION
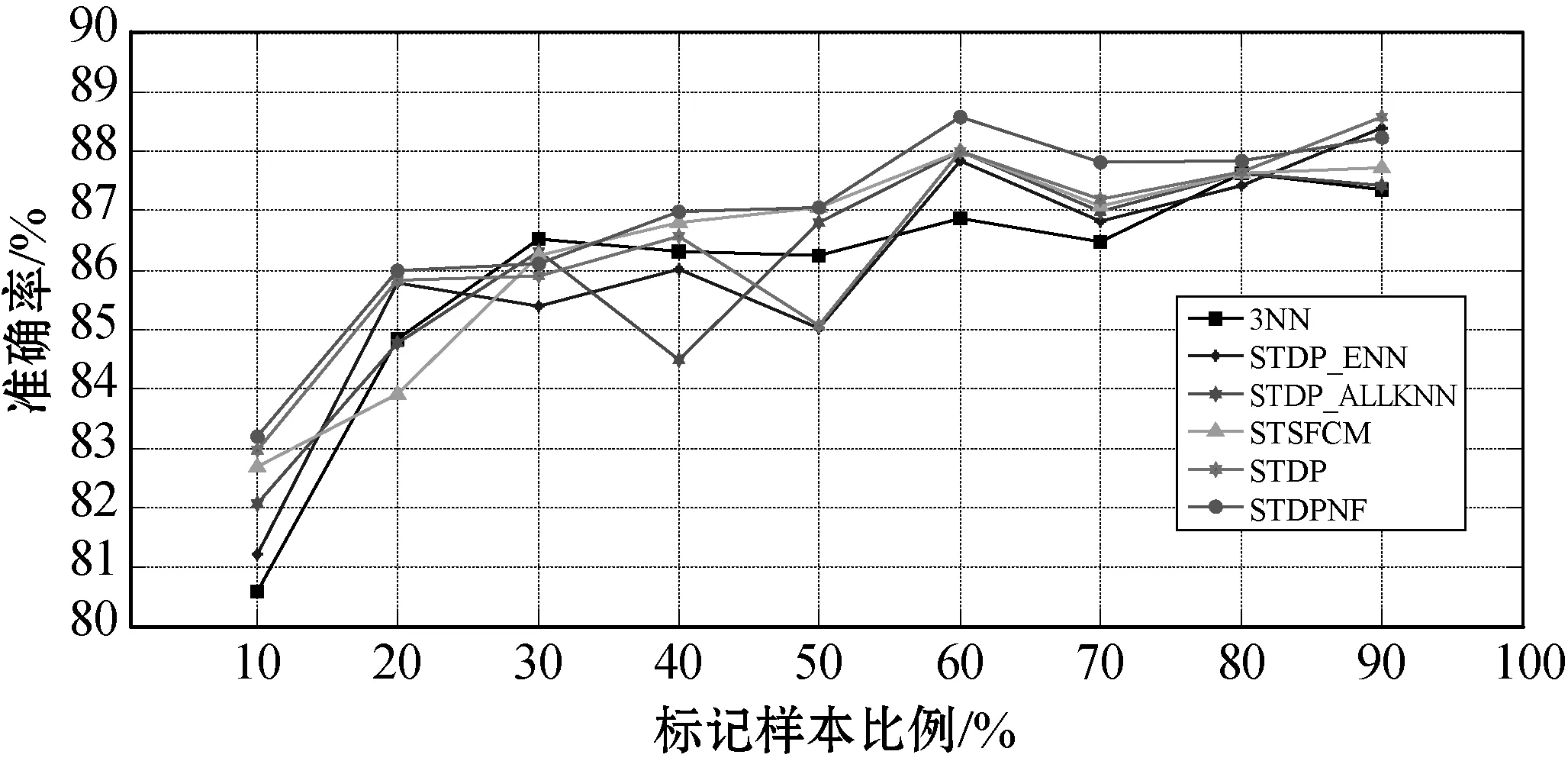
(d) 数据集:ECO
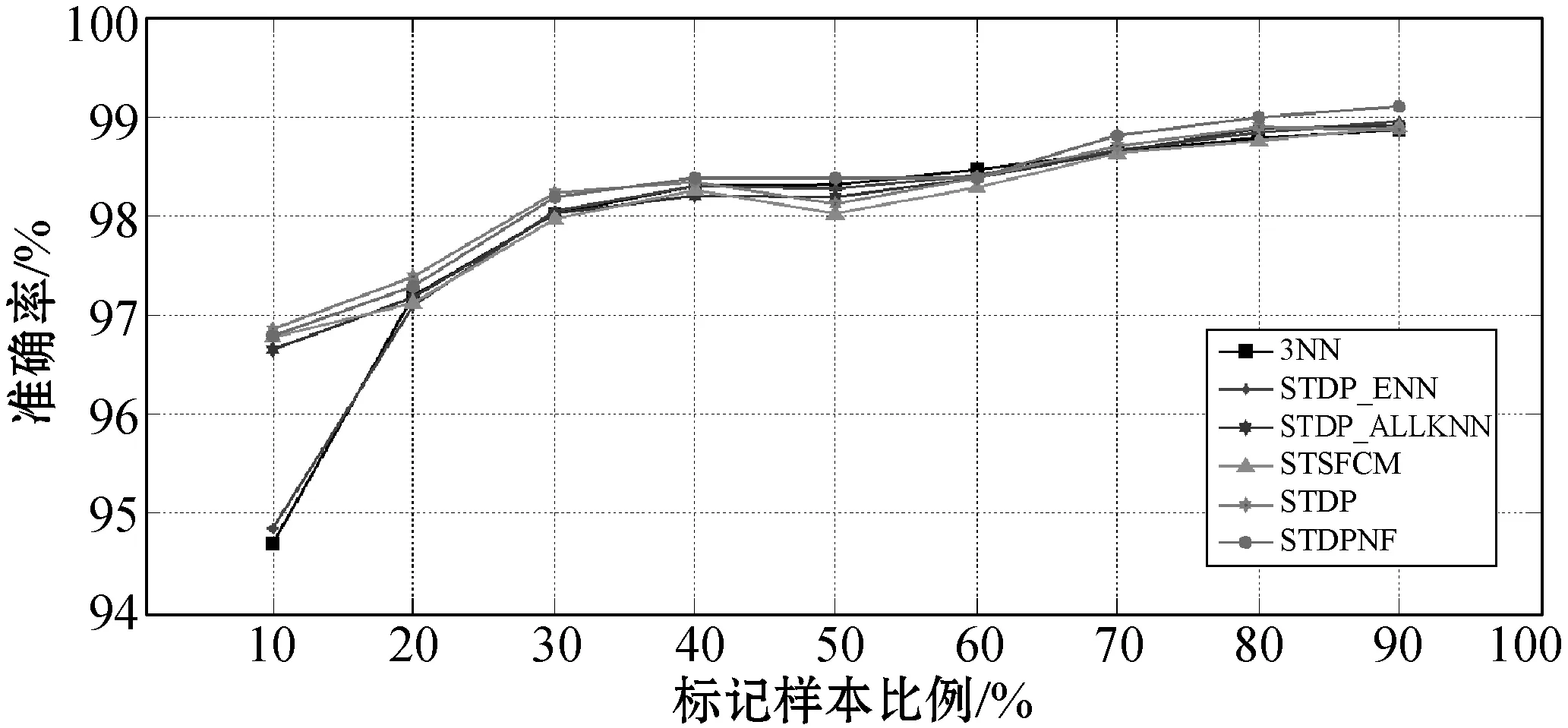
(e) 数据集:WIL

(f) 数据集:BRT图6 算法ACC与标记样本比例的关系
从图6可以看出,所有算法的ACC随L的比例的增加而增加。当L的比例相对较高时,所有算法均获得相似的结果。此外,在L比例不同的情况下,提出的算法在LIV、LON、ECO和WIL数据集上也取得了良好的结果。具体地,还可以发现,当L的比例相对较低时,提出的算法在LIV、LON、ECO和WIL的数据集上都能取得更好的效果。原因是当L较小时,提出的算法可以用ENaNE通过利用U的附加信息来滤除噪声实例。根据先前工作的介绍,大多数现有的局部噪声滤波器需要更多的L才能更好地工作。相比之下,即使L不足够,提出的算法中使用的ENaNE也可以有效地删除标记错误的实例。因此该算法具有明显的优势。
尽管所提出的算法在BRT和IMS数据集上的效果不佳,但是所有算法在具有不同L值的BRT和IMS数据集上都具有相似的结果。另外,当将数据集ION上的L的百分比从20%增加到40%时,STDP_ENN、STDP_AKNN、STSFCM、STDP和STDPNF的准确性会大大降低。这是因为STDPNF的ENaNE中的自训练方法错误地预测了未标记样本的类标签,这削弱了STDPNF的ENaNE的能力,另外STDP、STSFCM、STDP_ENN和STDP_ALLENN向L添加了错误预测的未标记样本。
实验四:训练时间测试。很难分析自训练方法的时间复杂度。因此,本节将通过在9个数据集上比较表2中列出的所有自标记算法中的中央处理器(CPU)运行时间来说明STDPNF的计算效率。在STDPNF中发现结构的时间复杂度为O(n2),在STDPNF中搜索NaNs的时间复杂度为O(nlogn)。STDPNF中ENaNE的运行时间取决于ENaNE中自训练方法的运行时间。
表7中给出了相应的算法执行时间对比结果。尽管STDPNF比STDP消耗更多的时间,但它并不是最耗时的算法。实际上,因为MLSTE中的ENN和SETRED中的CEWS具有较高的时间复杂度(O(n3)),所以SETRED和MLSTE比STDPNF消耗更多的时间。此外,在某些数据集,例如UKM、SPH和LIV上,STSFCM还比STDPNF消耗更多的时间,因为SFCM需要在自训练过程的每次迭代中运行。权衡STDPNF的优缺点,STDPNF的计算效率是可以接受的。
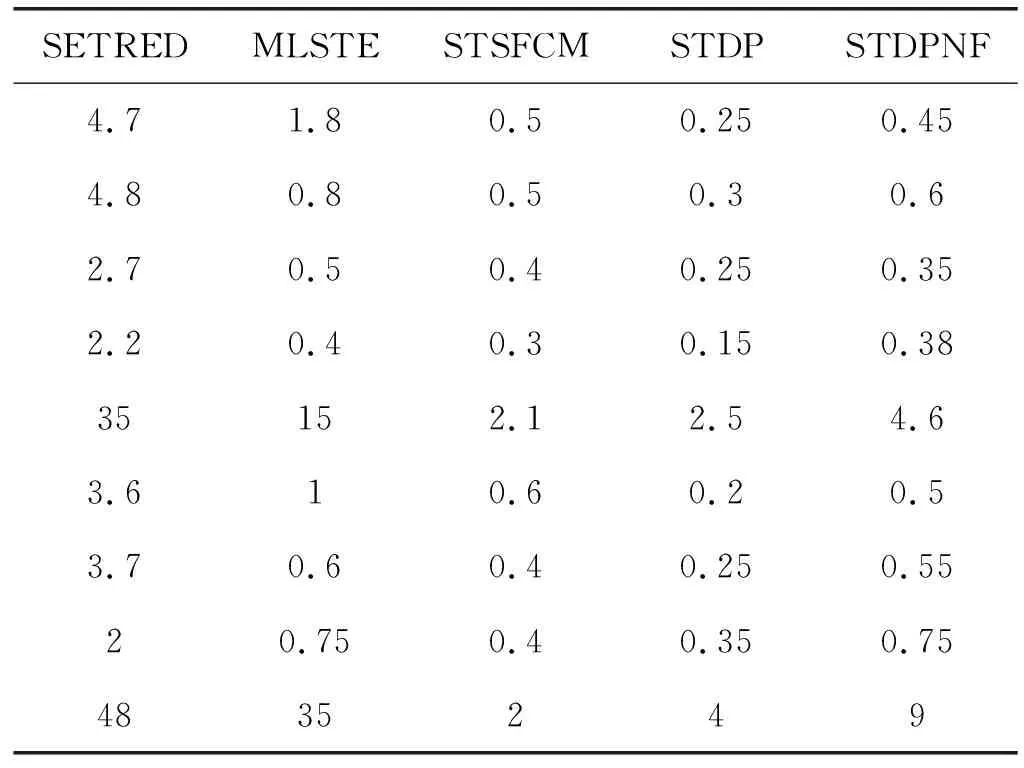
表7 不同算法训练时间对比结果 单位:s
4 结 语
针对自训练方法中局部噪声滤波器存在的参数依赖性以及仅使用标记数据来删除标记错误样本等局限性,提出了一种基于密度峰值和无参数局部噪声滤波器自训练方法。通过四个对比试验可得出如下结论:
(1) 所提出算法在提高基分类器KNN的分类精度方面比现有工作更有效。
(2) 所提出算法中使用的局部噪声滤波器克服了现有局部噪声滤波器的技术缺陷。它能够不依赖参数选取,更具有自适应性。即使标记数据不足,它也可以通过利用未标记数据的附加信息来删除标记错误的样本,验证了该算法具有更好的泛化能力。
(3) 所提出算法的计算效率和执行时间处在可接受的范围内。
下一步应将所提出的算法应用于多标签分类任务。
