基于最优插入子集的动态规划算法求解旅行商问题
2023-01-31段隆振
但 开 段隆振
(南昌大学信息工程学院 江西 南昌 330031)
0 引 言
经典的旅行商问题(Travelling Salesman Problem,TSP)可以描述为:给定一组城市,这些城市之间的距离已知,寻找一条经过所有城市一次且仅一次并返回起始城市的最短路线。旅行商问题有着广泛的实际应用,生活中经常出现的各类组合优化问题都可以归为旅行商这类问题。如物资运输路线中,汽车应走怎样的路线使路程最短[1];大型工业制件在增材制造中的路径规划[2];CNC在线检测中,如何尽可能缩短检测路径长度[3];在航海相关问题中,无人驾驶船舶路径规划或船舶航线自动生成[4];多无人机协同作业中,规划出符合无人机机动性能约束和安全要求的最优航迹的问题[5]等。
三角不等式是TSP的一个很自然的限制:对任意三座城市A、B和C,从A到C的路程加上从C到B的路程应该大于等于从A到B的路程。旅行成本是对称的,而且满足三角不等式的题目称为TSP的度量(metric)题目。当把城市视为平面上的点,许多距离计算方式都满足这个自然条件,例如城市距离为欧几里得距离(Euclidean distance)、曼哈顿距离(Manhattan distance)、切比雪夫距离(Chebyshev distance)的TSP都属此类。如果两个城市之间的距离是相应的欧几里得距离,且两个城市之间的距离在两个方向上都是相同的,这样的TSP称为对称的Euclidean TSP。许多自然实例都是对称的Euclidean TSP。
旅行商问题的最优化求解非常困难,其最根本的原因是求解这些问题的现有算法需要极长的运行时间以及极大的存储空间,以至于根本不可能在现有的计算机上实现,即存在所谓的“组合爆炸”。例如31个城市的旅行商问题,使用穷举法需要遍历30!/2种排列。如果使用目前我国排名第一的超级计算机——神威太湖之光(Sunway TaihuLight,含有10 649 600个处理器,运算速度可达每秒125 436万亿次),假设检验每条路线只需要一次算术运算,那么解决这道31个城市的TSP问题预计需要超过3 352万年。
通过Cook[6]和Karp[7]的理论,可以将旅行商问题和许多其他问题联系起来。很多的组合优化问题,比如背包问题、车间调度问题、分配问题都和旅行商问题同属于NP完全问题。如果其中任意一个能用多项式确定性算法解决,那么其他所有NP完全问题也能用多项式算法解决。事实上,有很多方法本来是研究旅行商问题时提出来的,经过不断的发展,后来又推广到了其他NP完全问题上去。
动态规划(Dynamic Programming)是解决多阶段决策过程最优化的一种数学方法。在多阶段决策过程中,动态规划方法将问题的过程分成几个相互联系的阶段,恰当地选取状态变量和决策变量及定义最优值函数,从而把一个大问题化成一组同类型的子问题,然后逐个求解。即从边界条件开始,逐段递推寻优,在每一个子问题的求解中,均利用了它前面的子问题的最优化结果,依次进行,最后一个子问题所得的最优解,就是整个问题的最优解。动态规划的方法在电网调峰[8]、航天航空[9]和保险金融[10]等领域中都有广泛的应用。
已知求解旅行商问题的精确算法的运行时间界限是Held-Karp[11]动态规划法的O(n22n),这个纪录已经保持了58年。如果能突破这个界限,哪怕只是一点点改进,也有可能获得更快的时间界限,就有可能适用于实际应用,从而推进旅行商问题的实战前线。
1 简单插入与两个猜想
1.1 简单插入
插入算法(Insertion Algorithm)的思路是从一条周游几个城市的子路线出发,逐个增加新的城市并插入到合适位置,直至得到一条包含所有城市的新路线。算法核心部分的伪代码为:
Begin
设算法运行过程中M为当前子路线;
根据新城市选取函数选取待插入城市i;
根据插入位点选取函数选取插入位点p;
M.insert(p,i);
if所有城市均在M中:
返回M;
else:
进行下一步插入操作;
End
其中插入位点选取的规则是遍历所有可插入位点,计算插入后的路线长度,其中最短路线长度所对应的位点作为插入位点。将这条规则称作简单选取规则,通过简单选取规则进行的插入称为简单插入。
1.2 一个插入法的实例
例1十三个城市的TSP,城市从0到12依次编号,城市横坐标依次为{466,826,555,79,781,251,329,336,978,793,489,496,735},城市纵坐标依次为{407,389,485,264,618,766,640,670,195,15,714,218,438}。
其最优路线为[7,6,2,0,3,11,9,8,1,12,4,10,5],最优路线长为3 082个单位长度,如图1所示。
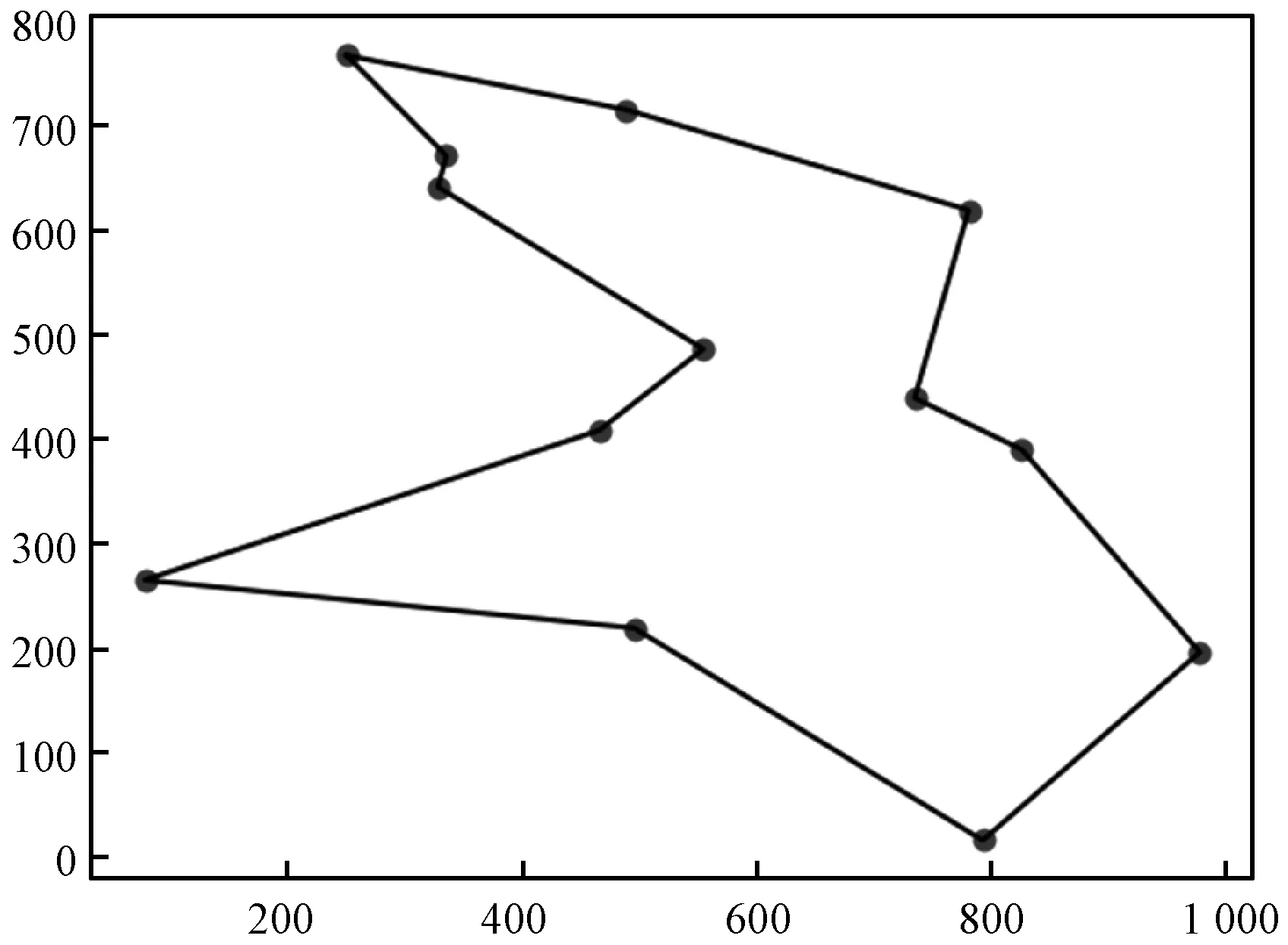
图1 例1的最优路线
对于旅行商问题,有两个最基本定理,分别是交叉避免和凸包规则。
交叉避免:最优路线不会自交,因此在解题过程中应避免出现交叉的情况。
用一步2-opt可以证明这个事实,若巡回路径中存在交叉路径,则打开交叉路径得到的路径长度一定小于原路径长度。
凸包规则:最优路线中经过边界各点的顺序和凸包边界经过边界各点的顺序相同。它们在边界上的顺序与在最优路线上的顺序相同,其余城市的顺序则是由边界向内侧拐入短的子路径而得。
最优路线需要避免自交,所以经过边界各点的顺序必须和凸包边界经过边界各点的顺序相同。
对于例1,使用凸核插入法,即初始子路线从城市点集的凸包开始,插入位点选取规则不变,遍历所有可能的插入顺序,可能得到的结果只有4种,如图2所示。其中路线长度最小为3 106个单位长度,大于最优路线的3 082个单位长度。
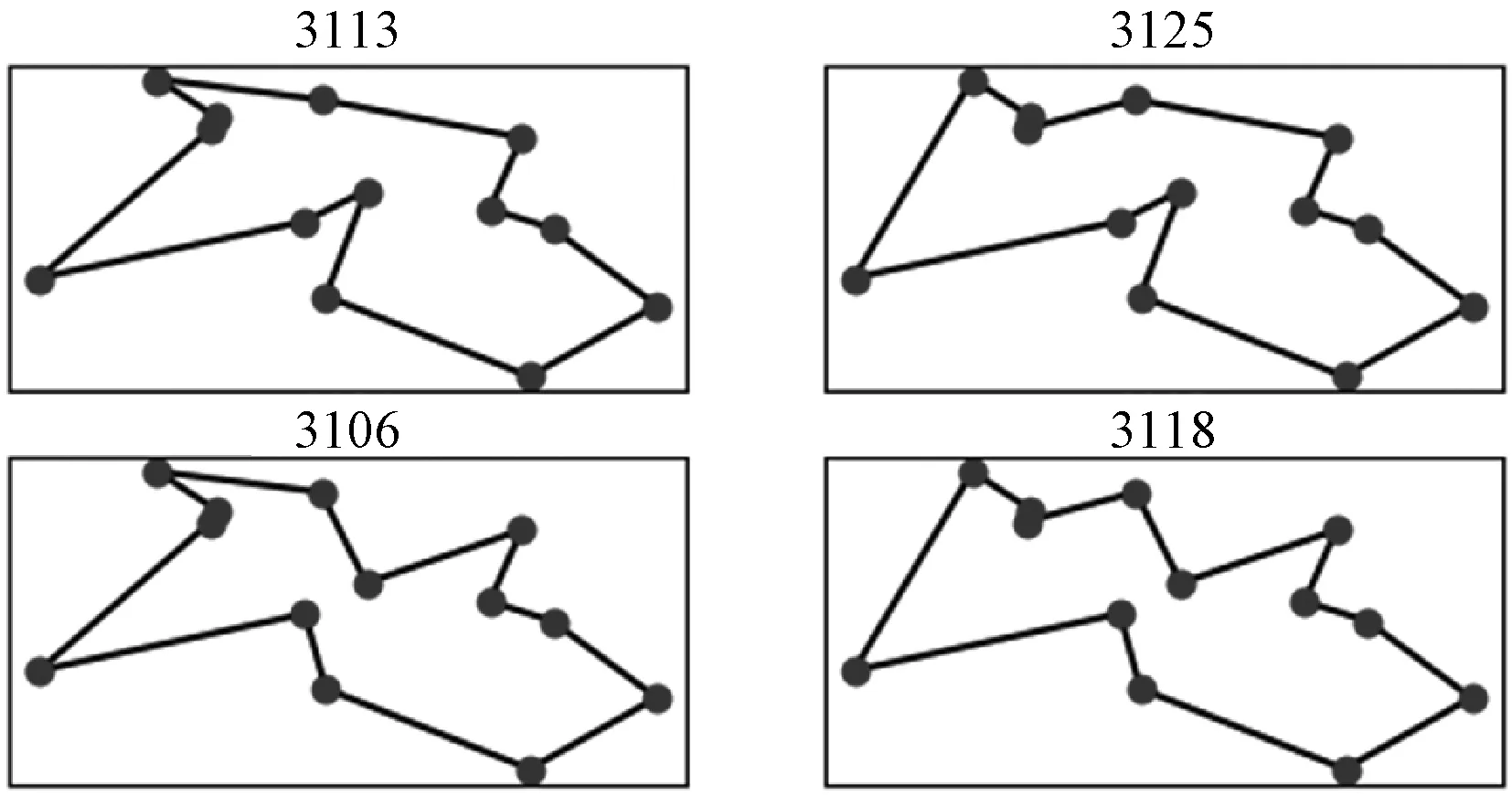
图2 凸核插入法求解例1的所有可能结果
作为近似算法而言,在插入法中加入能够把握整体形状的初始子路线可以在插入城市的过程不断完善细节,往往能得到比不加入初始子路线更优质的路线。但在寻找最优解方面,由于插入法在插入过程中不会改变已插入的城市排列,所以加入的初始子路线首先必须保证其排列与其在最优路线上的排列一致。即使找到凸包这种特殊的初始子路线满足排列一致的条件,例1也说明了其有可能无法达到最优解。
1.3 简单插入最优性猜想
例1已经指出增加初始子路线的做法会使得最优解被排除在算法的解空间之外,那么,不指定初始子路线,用简单插入的方式,遍历所有的城市插入顺序,是否必定能得到最优解呢?对于例1,按照插入顺序5→10→4→12→11→1→8→6→2→0→9→3→7,可以得到最优解,如图3所示。
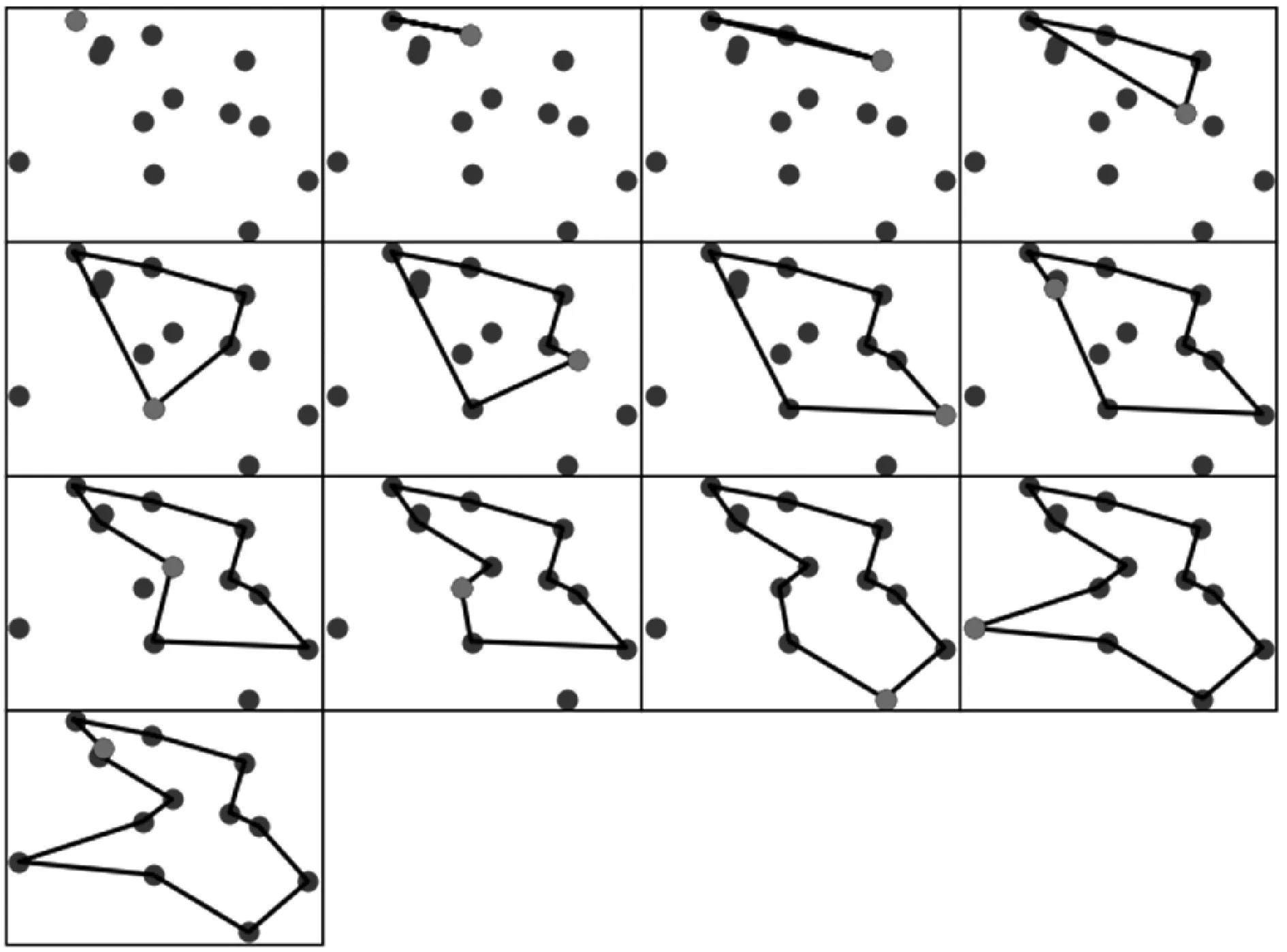
图3 不指定初始子路线基于简单插入的例1最优解插入过程
针对对称的Euclidean TSP,考虑如下猜想。
简单插入最优性猜想:对于任意TSP,依据简单选取规则的插入法的所有可能中,必定包括TSP的最优解。
1.4 插入过程与插座
定义1对于任意的TSP,从其最优路线中选择任一城市a剔除,剩下的城市排列为城市a的插座。
定理1通过将a简单插入a的插座中得到的必定是最优路线。
证明:用反证法。
若将a简单插入a的插座中得到的不是最优路线,设a插入的位点为i,最优路线中a的插入位点为j,根据简单插入的定义,有插入i后的路线长度tour(i)小于插入j后的路线长度tour(j),这与最优路径长度最短的定义矛盾。证毕。
插座本身可以看作原问题规模减一的TSP,如果插座中的城市排列恰好是这个子问题的最优解,这样的插座称为同型插座,其他的不是子问题最优解的则称为异型插座。城市数量为n的TSP,插座总数为n。
1.5 同型插座猜想
易知,存在异型插座数量为0情形(n个城市的凸包),那么存在同型插座数量为0的情形吗?
针对对称的Euclidean TSP,考虑如下猜想。
同型插座猜想:对于任意TSP,必然存在同型插座。
根据定理1,对于任意TSP,其最优解可以由其中一个城市通过简单插入操作插入到与其对应的插座中得到。而根据同型插座猜想,对于任意TSP,必然存在同型插座,同型插座即为子集的最优解。结合定理1以及同型插座猜想,由数学归纳法即可推出下面的同型插座猜想的推论。
同型插座猜想的推论:对于任意TSP,依据简单选取规则,必然存在这样插入过程:插入中每一步的子路线都是当前的TSP最优解。
这样的插入过程中可以根据子路线中不同城市的数量分为n个阶段,每个阶段所有子路线的集合称为该阶段的最优插入子集。
图3中的插入过程就是这一推论的一个例子,在每一步的插入过程中,其插入后形成的路线都是当前已插入城市组成的子问题的最优解。
1.6 同型插座数量分布规律的统计分析
在1 000×1 000正方形区域内随机取m个点的坐标数据,这些数据构成了城市规模为m的旅行商问题,用X表示这个旅行商问题的同型插座数量,X是一个随机变量,它的概率密度记为f(x),其均值为μ,标准差为σ。设X1,X2,…,Xn表示来自f(x)的一列独立的随机变量。根据中心极限定理,当n很大时(在实际的抽样中,一般当样本容量大于等于30时就可以应用中心极限定理),随机变量Yn近似地服从正态分布N(nμ,nσ2)。
已知Yn的概率分布模型,可以利用样本的密度构造似然函数求出μ和σ2的极大似然估计值。Yn的似然函数为:
(1)
对式(1)两边取对数:
(2)
对式(2)求偏导:
解得:
考虑一般情况,假设城市个数为n的所有TSP组成一个集合Un,用Cm表示Un中异型插座的数量为m个的所有元素集合,m=0,1,…,n。如果同型插座猜想成立,那么对于任意Un,可知Cn=∅。考虑三个城市的TSP,其所有排列方式都是等价的,换言之,三个城市的TSP只有一条路线,这条路线即为最佳路线。根据插座理论可知,四个城市的TSP有四个插座,这些插座都是三个城市,又因为三个城市只有一种可能路线(即最佳路线),所以四个插座皆为同型插座。如果同型插座猜想不成立,则存在城市个数为k的TSP不存在同型插座。综上所述,k应该大于等于5。
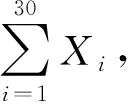
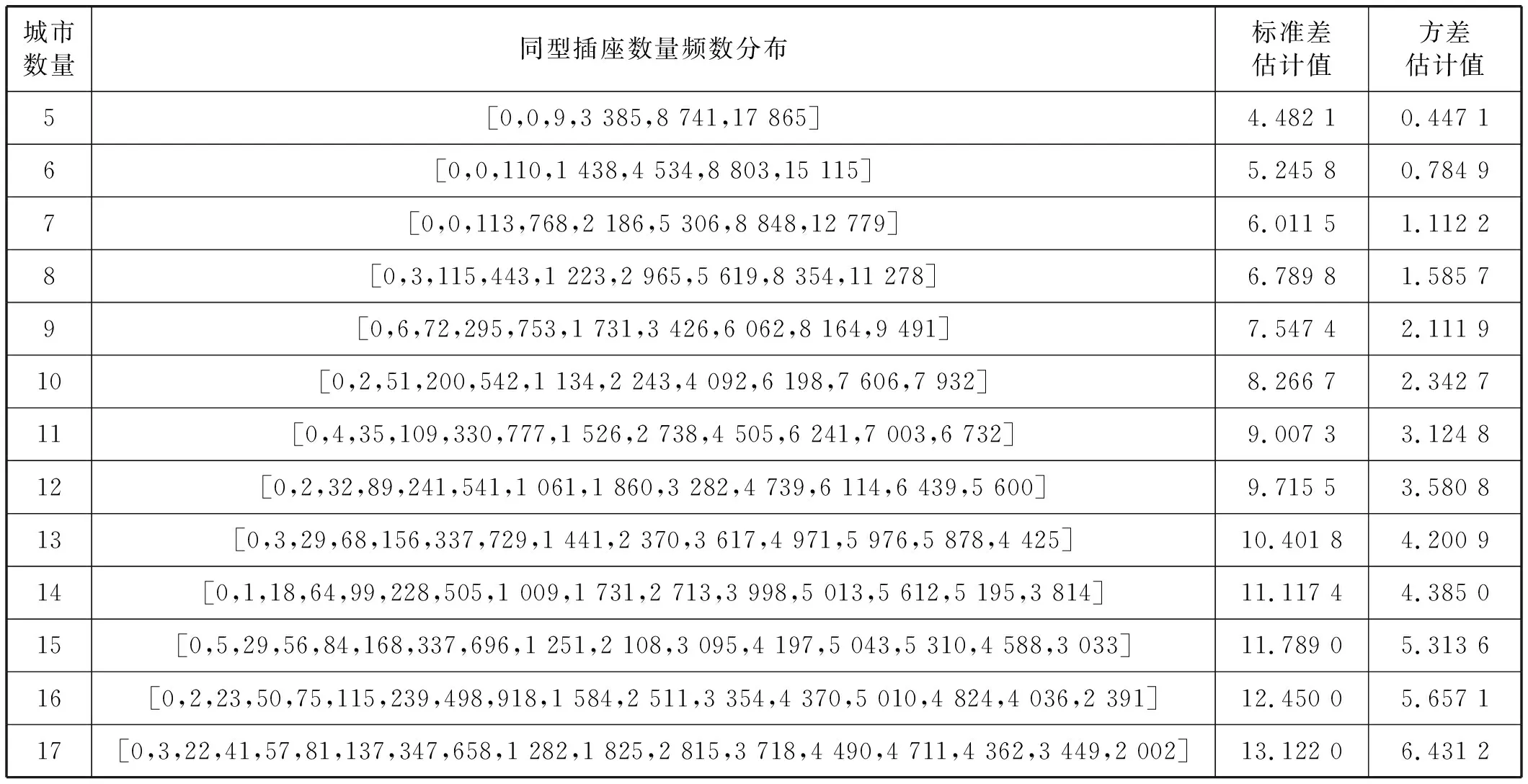
表1 插座型号数量分布实验的数据
从表1同型插座数量频数分布的实验数据中可以看出,同型插座为1的情形,在城市数量大于7时开始出现,且不同城市数量的3万次独立实验中出现的频数均为个位数,计算其平均频率为0.000 103;同型插座为0的情形,在实验中没有出现过一次。这样的实验结果有两种可能:(1) 同型插座猜想成立,任意TSP至少存在一个同型插座;(2) 存在同型插座猜想的反例,即存在同型插座数量为0的TSP,但反例的出现是极小概率的事件,以至于在本次实验中未出现。
假设同型插座猜想存在反例。根据伯努利大数定律,当n足够大时,事件A出现的频率将接近于其发生的概率。比如同型插座数量为1的情形,用频率估计其概率,概率约为万分之一。同型插座数量为0的情形,频率为0,根据假设其概率不为0,那么,其概率必然远小于万分之一。
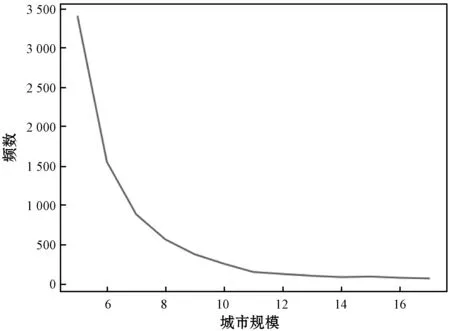
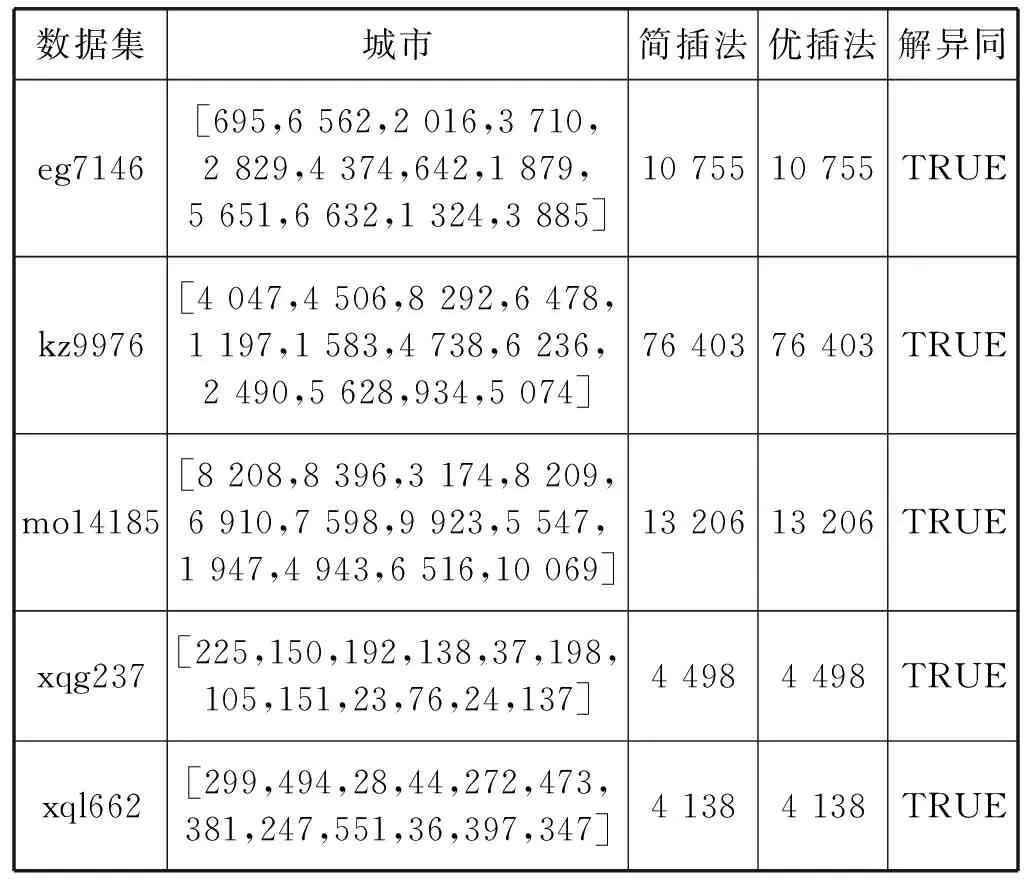
从图4中可以看出,同型插座的分布形态随着城市个数的增加,越来越接近两边少、中间多的钟形分布概率模型。在典型的钟形分布即正态分布中,如果a小于标准差μ,那么P{x 图4 同型插座的频数分布 如果考虑同型插座数量小于4的情形,从图5中可以看到随着城市个数的增加,其出现的次数是递减的,这意味着随着问题规模增加,同型插座数量小于4出现的概率在下降。 图5 同型插座数量小于4的频数随城市规模的变化 综上所述,同型插座猜想的反例即使存在,也是小概率事件,而且随着城市规模越大,这个概率呈减小的趋势。 考虑n座城市的TSP题目,城市从1到n依次编号命名。依据简单插入子集中的城市数量可以划分为不同的阶段,用k表示,k分别等于1,2,…,n。 以城市集{1,2,3,4,5}为例,城市数量为3的子集有{1,2,3}、{1,2,4}、{1,2,5}、{1,3,4}、{1,3,5}、{1,4,5}、{2,3,4}、{2,3,5}、{2,4,5}、{3,4,5}共10个,因为三个城市的路线实际只有一条,这里每一个城市子集对应一个子路线,所以第三阶段有10个状态。 其城市数量为4的子集有{1,2,3,4}、{1,2,3,5}、{1,2,4,5}、{1,3,4,5}、{2,3,4,5}共5个。其中{1,2,3,4}可由{1,2,3}插入4、{1,2,4}插入3、{1,3,4}插入2、{2,3,4}插入1这四种情况得到相应的简单插入子路线,这四条路线有可能重复,记录下不同的成为第四阶段的一个状态。一般第四阶段以后,每个城市子集都有可能对应多个子路线,至少为一个,且不同题目对应不同的数量。 第五阶段的城市子集为{1,2,3,4,5},可由{1,2,3,4}插入5、{1,2,3,5}插入4、{1,2,4,5}插入3、{1,3,4,5}插入2、{2,3,4,5}插入1得到。以{1,2,3,4}插入5的情况为例,在第四阶段找到城市子集{1,2,3,4}对应的简单插入子路线,假如有a条子路线,那么就将城市5逐个插入其中,记录下不重复的新的子路线。 在最后一个阶段的状态转移完成后,会得到{1,2,3,4,5}所对应的多条简单插入子路线,根据简单插入最优性猜想,最优解必在其中,此时只要计算这些路线的长度,最短的那条即为该旅行商问题的最短旅行路线。 依据同型插座猜想的推论,TSP的最优解可以通过同型插座进行简单插入得到,城市个数为n的TSP有n个插座,这些插座可能为同型,也可能为异型。同型插座猜想指出这n个插座中必然存在一个同型插座。n个插座对应n个TSP的子问题,这些城市个数为n的TSP都有最优解,它们与插座的关系是,同型插座等价于子问题的最优解,异型插座不是子问题的最优解。 假设我们知道所有城市个数为n的子问题的最优解,那么这些最优解中必然至少有一个会是原问题的同型插座,对所有这些最优解进行简单插入,假设a为插入城市,那么可能的结果只有两种,(1) (城市a)+(a的同型插座)=最优解;(2) (城市a)+(非插座)=非最优解,由前文得知第一种结果必定存在,因此可以遍历所有结果,其中路线长度最小的即为最优解。同时,城市个数为n-1的子问题的最优解可以如法炮制,从城市个数为n-2的子问题中得到,即满足无后效性(马尔可夫性)。因此,可以从城市个数为3(3个城市无须排列即为最优路线)开始,逐步求得城市个数为4,5,…,n的最优解。 根据同型插座猜想的推论,必然存在这样插入过程:插入中每一步的子集都是当前的TSP最优解,这样的子集称为最优插入子集。这是简单插入最优性猜想的一个特例。与基于简单插入子集的动态规划法相比,新动态规划法只需关注简单插入子集中最优的部分,有效减少了每个阶段的状态数量,因此,算法的效率得到了提升。 城市个数为n的TSP,共有2n个子集(包括它自己和空集,事实上算法是从城市数目为3的子集开始的,为方便计算,此处增加到最大值2n),在每一个子集中,至多有n个插座,对每一个插座,主要操作为复杂度为n的简单插入。2n乘以n再乘以n,所以新动态规划法的时间复杂度为O(n22n)。 由于动态规划法本身存在的“维数障碍”,在电子计算机上计算时,每递推一段,都必须把前一段算出的最优值函数在相应的状态集合上的全部值存入内存中,因而当维数增大时,所需的内存量会呈指数倍增长。在新动态规划法中,每一个城市子集都对应一个状态,一共有2n个城市子集,每个城市子集最多有n个城市,因此空间复杂度为O(n2n)。 算法运行的硬件环境为Intel Core i5- 3320M CPU,2.6 GHz,4 GB内存,开发环境为Python 3.7。实验采用TSPLIB上的不同数据集,验证算法在各种潜在样本上的有效性。实验采用了eg7146、kz9976、mo14185、xqg237和xql662的实验数据,每次实验随机选择数据集中的12个城市,用Held-Karp动态规划法(HK),基于简单插入子集的动态规划法(简插法),基于最优插入子集的动态规划法(优插法)计算得到结果,表2是一次实验的数据。 表2 在不同数据集上的一次实验结果 这样的实验重复进行一万次,实验结果解异同均为TRUE,即三种算法的解都是最优解。这初步表明在不同数据集中,基于最优插入子集的动态规划法能有效求得最优解。 基于简单插入子集的动态规划法的理论依据是简单插入最优性猜想。这一猜想理论上的证明或许能带来对TSP结构上的深入认识。 基于最优插入子集的动态规划法的理论依据是同型插座猜想。对于同型插座猜想,实验测试的统计分析表明它有可能存在反例,但是即使存在反例,其在实际情况中出现的概率极小。而且城市规模越大,反例出现的概率越接近0。 如果无数多的猴子在无数多的打字机上随机地打字,并持续无限久的时间,那么在某个时候,它们必然会打出莎士比亚的全部著作。这个设想本身在现实生活中是不可能重现的,就像一个房间内的空气总是均匀分布的。同型插座猜想可能也有类似的性质,理论上存在反例,但实际遇到的TSP都满足同型插座猜想。算法实现中采用了TSPLIB上的不同数据集,基于最优插入子集的动态规划法均能找到最优解,实验结果在一定程度上支持了这种观点。 新动态规划算法为求解旅行商问题提供了新的思路,对于认识、分析众多复杂问题具有一定的启示,对促进组合优化问题的研究有着积极的作用。如果将其与其他启发式算法融合或许会催生出性能优异的新算法,这将给实际解决大规模TSP问题提供新的方案。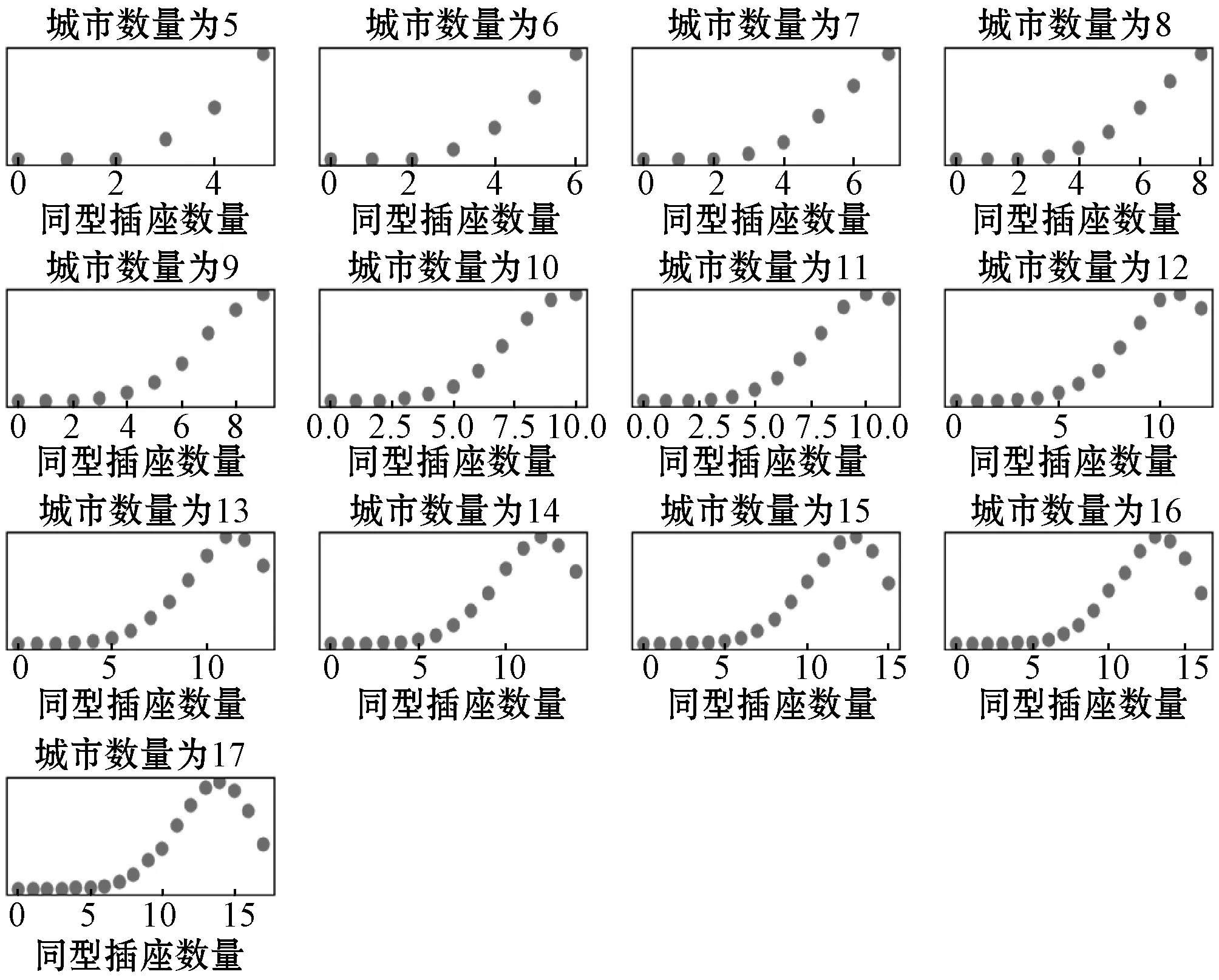
2 算法设计与实现
2.1 基于简单插入子集的动态规划法
2.2 基于最优插入子集的新动态规划法
2.3 算法实现
3 结 语
