基于MFCC特征的Wi-Fi信道状态信息人体行为识别方法

蒙倩霞 余 江 常 俊 浦 钰

(云南大学信息学院 云南 昆明 650500)

0 引 言

基于摄像机的行为识别方法无法监测光线盲区且隐私无法得到保障；基于雷达的部署成本过于昂贵，不适用于普通家庭；基于传感器的方法传感器一般佩戴于腰上，对于特殊人群来说，发生意外的时候无疑会增加危险指数。基于Wi-Fi信道状态信息(CSI)的活动识别系统克服了以上方法的缺陷，为活动识别提供了一种新的保密隐私、价格实惠且无须携带设备的方法。Wi-Fi信号易受到人体行为的影响，不同动作速度的快慢、维持的时间、身体的摆动幅度都会对CSI的变化造成不同的影响。因此可以根据CSI的变化去判别相应的行为。

Wi-Fall[1]跌倒检测系统分析出不同行为CSI幅值变化情况，平均实验精度为87%，但忽略了相位带来的影响。Emosens系统[2]从CSI识别用户的情绪状态，同样使用的是幅值特征。文献[3]提出了一种吸烟检测系统，用于室内环境吸烟行为检测，单个人的吸烟检测正确率为97.6%，但是多人条件下，性能急剧下降。文献[4]采用RNN网络可以有效识别其动作，穿墙识别精度高达95%以上。利用机器学习的方法虽然可以自动提取特征，识别精度也甚好，但是计算的复杂度很高，需要大量的数据训练且提取特征的合理性也难以解释。在最新的研究成果中，文献[5]提出了一种穿墙识别的结构，但仅限理论分析。文献[6]提出的TS-see系统同样也实现了穿墙识别。文献[7]提出在多人场景中无设备位置行为特征转换的问题，场景复杂化和多人适应性将是今后研究的重点之一。文献[8]利用CSI来识别驾驶员的注意力状态，获得了较好的识别性能。文献[9]利用多通道CSI测量数据转化二维图像，并使用深度学习进行训练和分类，这是基于观察而得到的方法。

本文利用CSI信号和声音信号传播相似性和两者共享带宽频谱的性质，把CSI信号当作语音流来处理，在CSI数据中提取了MFCC特征向量的统计特征以及提取了对数频谱能量特征，然后用蚁群和粒子群混合优化SVM(Ant Colony and Particle Swarm Optimization SVM，ACO+POS-SVM)[10]算法进行分类识别。实验结果表明，此方法在会议室场景的视距和非视距情况下都可以获得较好的识别结果。

1 基于CSI识别基本原理

1.1 Wi-Fi信号传播模型

由于Wi-Fi信号以多路径方式传播，环境中的物体会反射无线信号，那么一个发送信号x(t)就会通过多条路径到达接收器。假设x(t)通过N条不同的路径到达接收器，那么接收到的信号y(t)如式(1)所示。

(1)

式中：ak(t)是t时刻第k条路径的幅值大小；e-j2πfτk(t)是第k条路径上的相移；τk(t)为其传播延迟；e-j2πΔft是发送器和接收器之间的载波频率差Δf引起的相移。如图1所示。

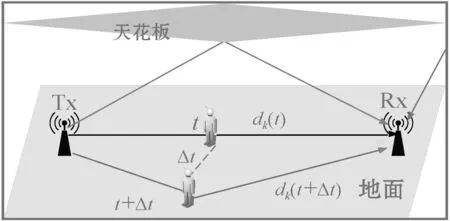
图1 行为引起的多径变化

当人在t到t+Δt的时间内在发射机和接收机的视距之间活动时，第k条路径上的信号由dk(t)变化到dk(t+Δt),此时接收端产生传播延迟相移τk(t)=dk(t+Δt)/c，则根据λ=c/f可以得到该条路径上的相移为e-j2πdk(t+Δt)/λ，其中：λ为波长；c为光速。这说明路径的变化会导致相应路径上Wi-Fi信号的幅度和相位的变化。

1.2 CSI数据模型

无线通信链路信道的特性通常是用信道信息状态来衡量，根据时域卷积性质，可以把式(1)表示为：

(2)

由式(1)和式(2)可得信道冲击响应(Channel Impulse Response，CIR)[11]为：

(3)

在IEEE 802.11n标准中，利用正交频分复用技术可以从物理层解析得到CSI数据。根据时频域的转换性质，可得到频域的信道信息响应H(f,t)为：

(4)

式中：ak(f,t)是t时刻第k条路径的衰减和初始相位偏移的复数值表示。

在MIMO系统中，设NTX为发射端的天线数量，NRX为接收端的天线数量。对于每个采样时刻t，CFR值构成NTX×NRX×i维的一个矩阵，其中i为Wi-Fi的子载波数。所以，在一段时间内，CSI由NTX×NRX×i维CFR值构成。H(f,t)也可以表示为：

(5)

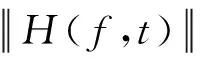
1.3 MFCC特征向量

MFCC向量是基于人耳对声音的频率感知的能力，其对应的梅尔频率与赫兹频率成非线性关系，频率与梅尔频率之间转换公式如式(6)所示[12]。

(6)

MFCC向量[13]提取过程中首先要对预处理过的信号进行分帧和加窗处理，常用的有汉明窗口如式(7)所示。

w(n)=0.54-0.46cos(2nπ/N-1)

(7)

式中：n是窗口的长度；w是窗口值。

然后，将各帧信号h(n)求快速傅里叶变换(FFT)得到各帧的频谱H(k)：

H(k)=FFT[h(n)]

(8)

(9)

式中：N是FFT的点数；m为滤波器的中心频率。Hm(k)是三角形重叠的窗口，其描述方程为：

(10)

在估计了加权频率系数之后，将梅尔频谱S(m)进行离散余弦变换(DCT),得到MFCC系数cg：

(11)

式中：cg为第g个MFCC序列，M为滤波器的个数。因为人体日常行为引起的CSI信号主要集中在低频阶段，因此在本文中提取了前12个序列。

2 系统设计

本文首先利用巴特沃斯滤波器去除了原始信号中的高频信号，然后再用PCA对信号进行处理，结果为一维时间序列。将预处理过的CSI数据当作时间流来提取MFCC系数特征，为了提升识别的精度，本文把统计特征(MFCC的均值、平均标准差和平均变化率)作为分类特征量。此外，CSI数据中的相位信息携带的信息是不可忽视的，为了充分利用相位信息，在特征向量中还增加了无偏移信号的对数能量，这个无偏移信号是经过相位校准之后得到的信号，最后进行数据匹配和行为判别，总体流程如图2所示。

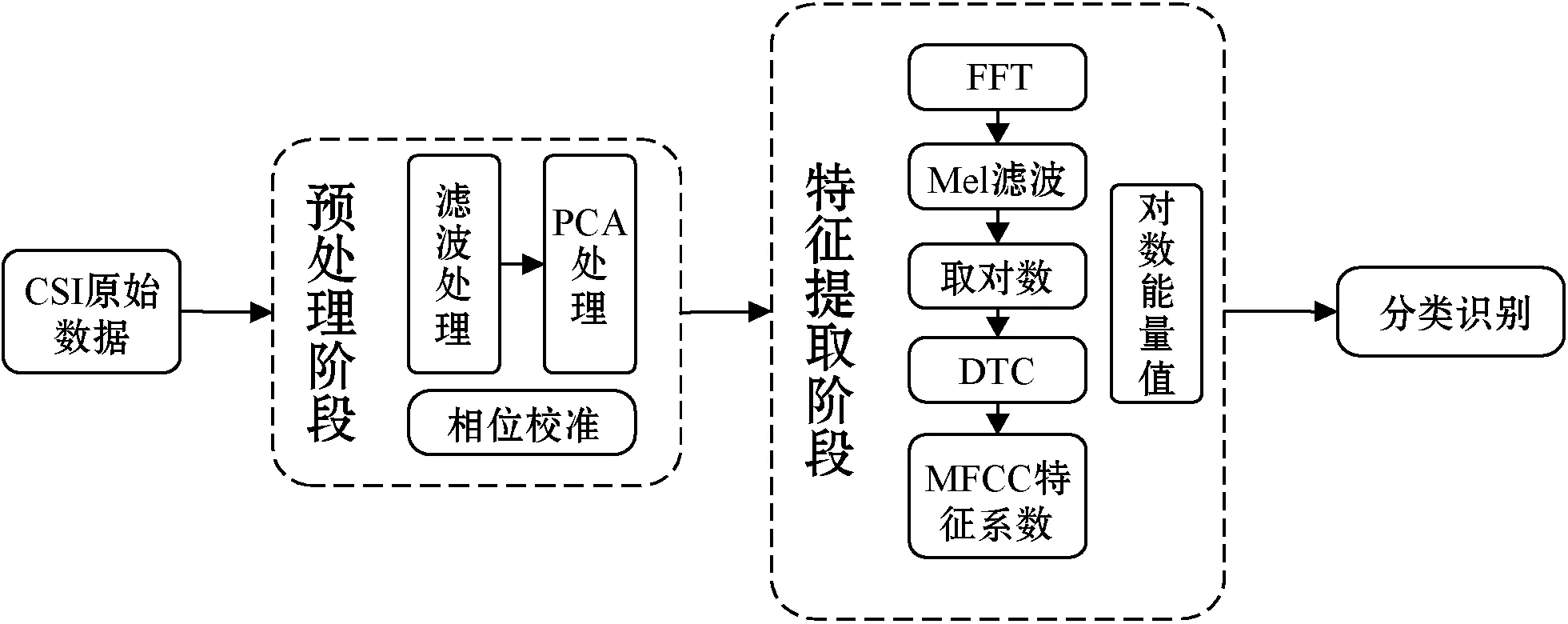
图2 总体流程

2.1 数据预处理

2.1.1滤波和PCA处理

在数据预处理阶段，本文使用巴特沃斯滤波器和PCA联合的方式对数据进行预处理，由于多径效应、设备和干扰等多种噪声的存在，原始采集的CSI信号毛刺较重，十分不平滑；另外，人的活动属于低频活动，需要把由于环境和设备而带入的高频滤除。经过巴特沃斯滤波器处理后的数据如图3所示。

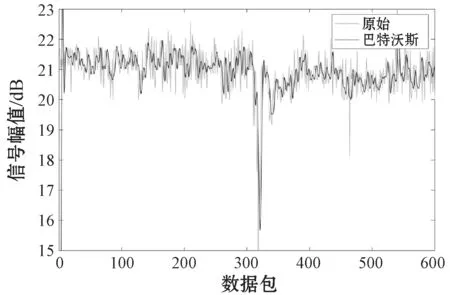
图3 滤波前后结果对比

在t到t+Δt的时间内，当信号的传播路径由dk(t)变化到dk(t+Δt)时，假设变化的路径为Δk(t)，那么Δk(t)=dk(t+Δt)-dk(t)，即dk(t+Δt)=dk(t)+Δk(t)，其中dk(t)是路径的初始长度，设φk=e-j2πΔft为子载波的初始相位，那么在t+Δt时刻副载波n的相位如式(12)所示。

cos(2πdk(t+Δt)/λn+φk)=

cos(2πdk(t)/λn+2πΔk(t)/λn+φk)=

cos(2πdk(t)/λn+φk)cos(2πΔk(t)/λn)-

sin(2πdk(t)/λn+φk)sin(2πΔk(t)/λn)

(12)

考虑到Wi-Fi信道中子载波的波长之间的差异很小,即两个不同子载波的波长存在λ1≈λ2的关系，且Δk(t)很小，则可以得到以下两式：

cos(2πΔk(t)/λ1)≈cos(2πΔk(t)/λ2)

(13)

sin(2πΔk(t)/λ1)≈sin(2πΔk(t)/λ2)

(14)

但是，式(3)中的两个子载波的常数项是不相等的，因为初始路径长度dk(t)远大于Δk(t)，因此，即使波长略有不同，两个子载波之间的初始相位差不可忽略。因此对于不同的副载波，CSI是具有不同初始相位的同一组时变波形的线性组合，因此，同一根天线上的CSI是相关的。图4(a)表示的是走动动作发生时一路天线上30个子载波的变化情况，可以直观地看出不同子载波的数据相关性大、冗余度很高。基于CSI流的相关性，本文采用了PCA对信号进行处理。由上文可知，在采集的CSI原始数据中，无论是静止环境还是有行为发生子载波之间都呈现出高度的相关性。但是从采集的角度来说，行为发生的时间只占据了整个采集过程的少部分而静态环境占据绝大部分。在主成分分析时，静态环境的信号与人体行为信号会一起在第一主成分中被捕获。然而，根据式(12)，可得知子载波的相位是两个正交分量的线性组合。根据PCA处理的正交性，可知在第一主成分中捕获的人体行为信号的所有信息也被捕获在其他主分量中，但是第一主成分中最多的是静态环境引起的噪声，因此，丢弃第一主成分可以消除静态噪声且人体行为信息又得到保留。本文方法中丢弃了第一主成分，并计算后五个主成分的平均值。经过PCA处理以后的走动动作的信号如图4(b)所示。

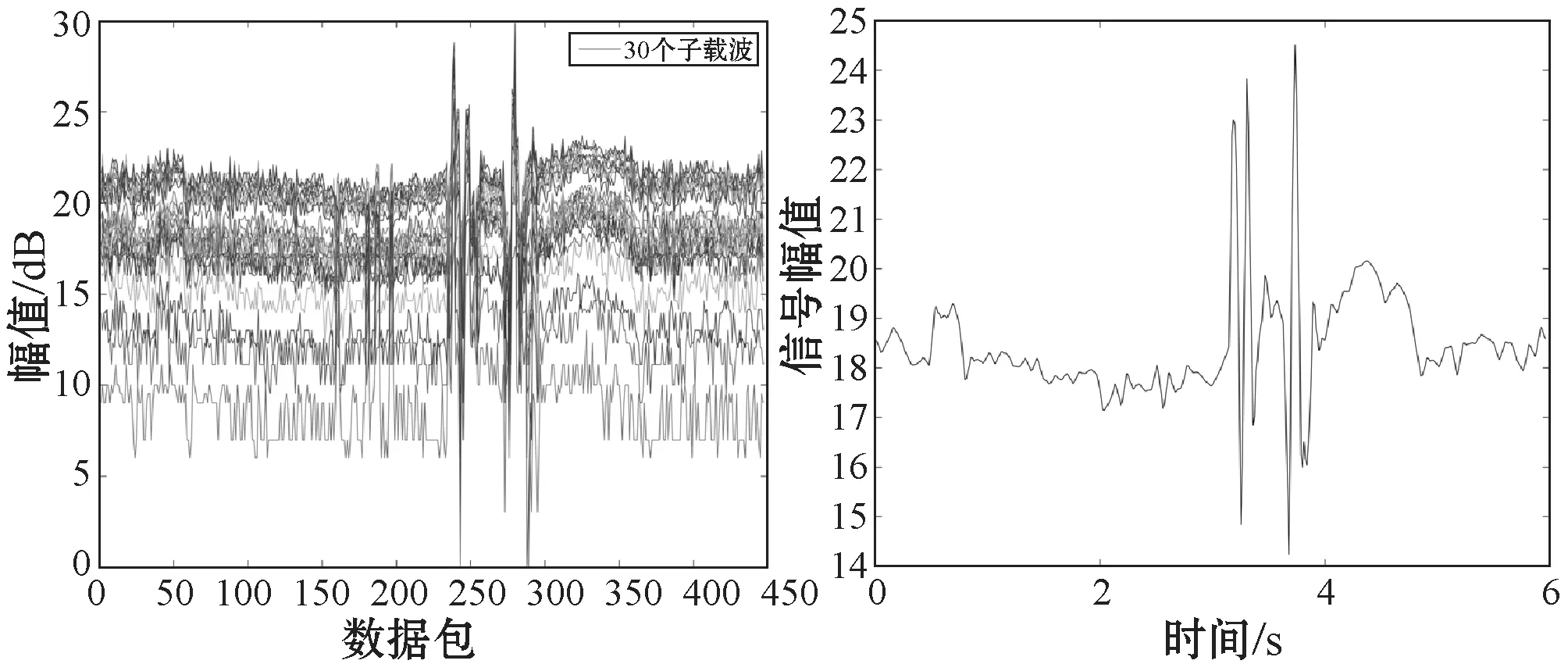
(a) 走动动作30个子载波 (b) 走动动作PCA处理结果图4 PCA处理结果对比

2.1.2相位校准

CSI的大量信息存在相位中，相位是不可忽视的一个方面。为了充分利用相位信息，在特征向量中还增加了无偏移信号的对数频谱能量特征，这个无偏移信号是经过相位校准之后得到的信号。子载波在不同的时刻的原始相位无规律可循，也无法使用。由式(3)可知，相位的偏差既有来自于设备自身误差也有来自于人体行为的变化引起的影响。如果将信号传播的路径分为静态和动态的话，在t到t+Δt的时间内，当信号的传播路径由dk(t)变化到dk(t+Δt)时，式(5)就可以表示为：

(15)

式中：Hs(f)表示静态路径的CSI。本文采用共轭乘法来消除时变随机相位偏移，跌倒动作校准前后的相位如图5所示。

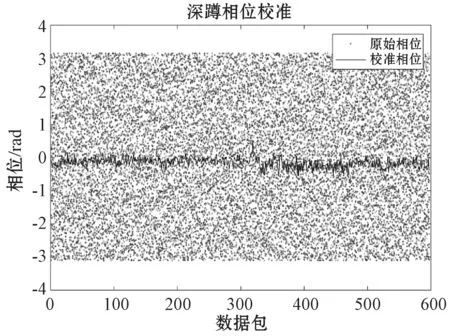
图5 跌倒动作相位校准

2.2 特征提取及行为识别

2.2.1MFCC特征向量提取

尝试在CSI信号中提取MFCC特征的原因有以下四点：(1) 带宽的相关性。在文献[14]对CARM数据集的每个日常活动的CSI信号平均占用的带宽进行了分析；其中包括了跌倒、深蹲和行走等动作，从统计数据中可以得出所用数据集的所有活动的带宽都在5 kHz以内，这和语音信号的带宽和能量分布极为相似。可以说由于活动影响CSI信号变化所占用的带宽是人类听力频谱的范围，大约为2～20 kHz，这为本文提取CSI数据的MFCC向量奠定了基础。(2) 信号的相似性。MFCC向量特征是识别语音信号的一个重要的特征，语音信号能量集中于低频段且变化迅速，从而使用密集的梅尔滤波器组放大这种特性。对于CSI信号而言，同样具备这样的性质。例如，当跌倒动作发生时，速度极快，CSI信号的变化也非常迅速。(3) 传播的相似性，语音和Wi-Fi信号分别是声波和电磁波，它们根据波动方程在测量环境中传播。它们遵循来自墙壁和其他障碍物的反射、折射和衍射的相同定律到达了它们的接收器，并由于类似的物理机制而变形。无论是声波和电磁波，都能产生时空共振现象。(4) 在文献[15]中已经证实OFDM信号的梅尔频率倒谱既保留了信号的基本特征，也移除了信号的冗余信息，相对原始接收信号的抗噪能力更加鲁棒[16]。相关研究表明，基于MFCC特征的方法能够有效实现多径信道下OFDM信号子载波多种调制方式的识别，且识别性能优于传统方法。

基于声音信号和CSI信号的这些共同特征，本文在CSI时间序列分类中提取MFCC向量特征，不同行为的对数MFCC向量如图6所示。

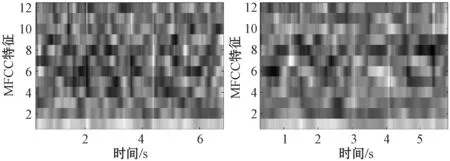
(a) 跌倒动作MFCC向量 (b) 深蹲动作MFCC向量

(c) 跳跃动作MFCC向量 (d) 走动动作MFCC向量图6 MFCC向量特征

不同行为CSI信号的MFCC向量互不相同，因此可以将CSI信号的MFCC向量作为识别不同行为特征参量。为了提高分类的准确性，本文提出使用MFCC向量的统计特征作为分类标准，分别是MFCC向量的均值、标准差和平均变化率作为分类特征量。根据1.3节中对MFCC向量的定义，MFCC向量的均值定义为：

(16)

式中：G是MFCC向量的个数。

平均标准差定义为：

(17)

式中：I表示帧数。

平均变化率定义为:

(18)

2.2.2对数频谱能量

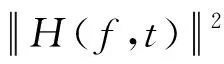
(19)

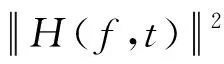
(20)

式中：H(f,t)表示经相位校准之后的CSI。

2.2.3识别方法

本文根据ACO和PSO优势互补特性，对原始SVM算法的惩罚参数和核函数参数进行优化[10]，具体流程如图7所示。在实验中，ACO参数设置为：ρ=0.65，Q=70，c1=c2=1.5，种群规模为30，迭代次数为45。PSO参数设置为：c1=c2=1.5，种群规模为28，进化次数为270。

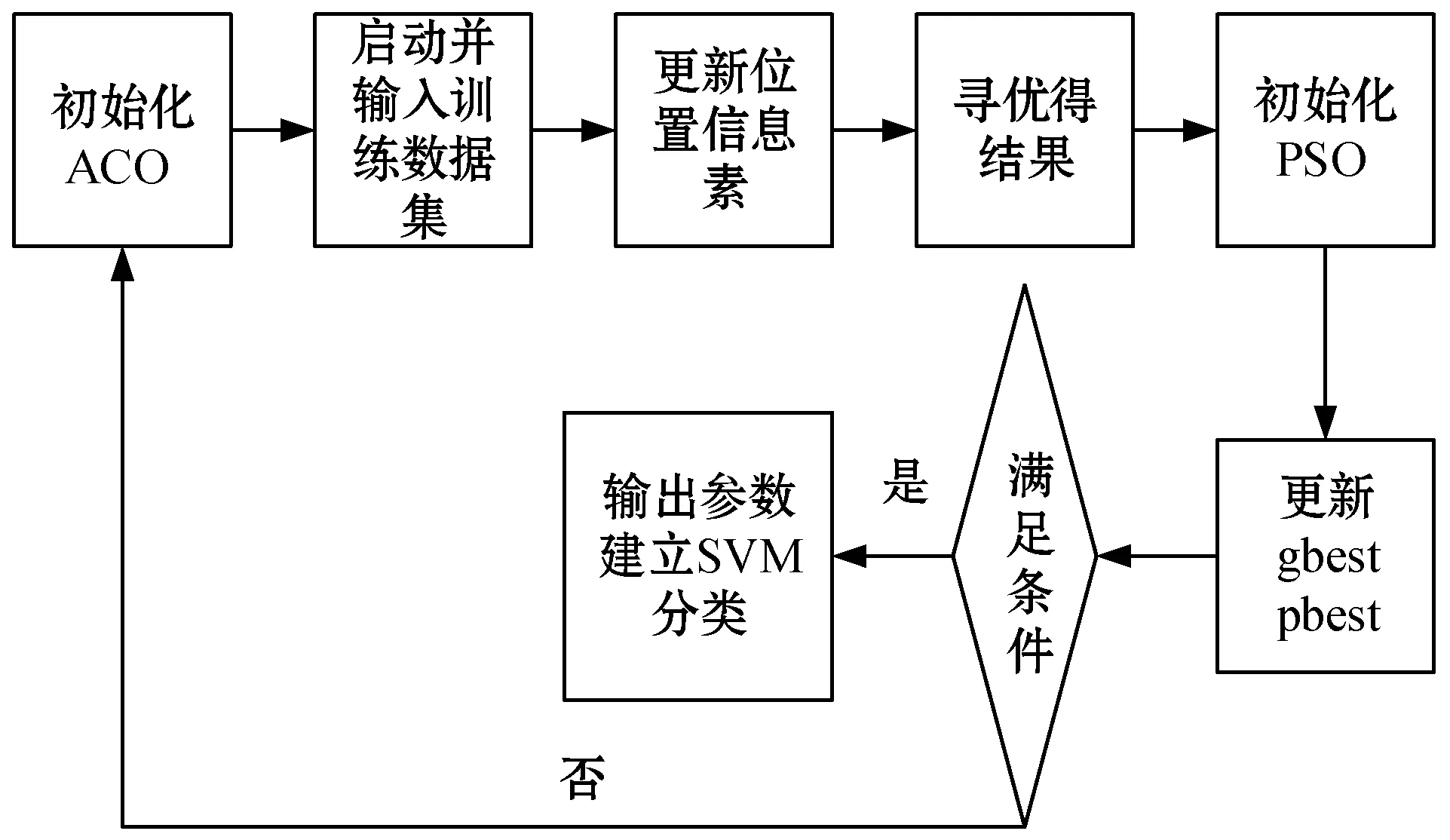
图7 算法流程

3 实验与结果分析

3.1 实验部署

实验的收发装置为两台配有Intel 5300网卡的主机，其中发射天线网卡上配有1根全向天线，接收天线网卡上均配有3根全向天线，为了得到稳定且采样率较高的CSI数据，采用Linux 802.11n CSI tool Monitor模式对网卡固件进行修改，带宽为40 MHz，中心频率为5 755 MHz。

实验的场景设置在环境较为复杂空间的会议室，平面图如图8所示。把收发装置放于50 cm高的桌子的对角，收发装置之间的距离始终保持4.5 m，本实验中邀请了3名志愿者，在收发装置的视距(图8中位置1)和非视距(图8中位置2和位置3)位置分别进行坐站、走动、跳跃、深蹲和跌倒五个动作，每名志愿者在每个位置重复每个动作30次，每次采集时间为30 s，第15 s的时候开始做动作，第30 s时候停止，重复此过程，接着采集下一个，总共采集1 350个样本。其中：1 000个样本用来训练；350个样本用来测试。

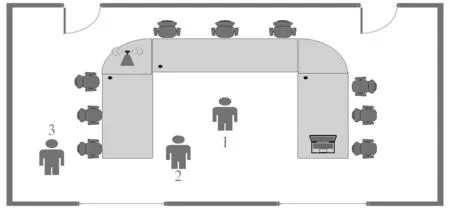
图8 实验场景

3.2 实验结果分析

3.2.1分类算法的性能分析

表1表示的是用SVM和ACO+POS-SVM[10]对志愿者的五种行为(坐站、走动、跳跃、深蹲和跌倒)进行上述特征识别的结果。结果表明，使用ACO+POS-SVM比SVM平均精度分别提高了5.1百分点、4.8百分点、5.3百分点、4.5百分点和5.1百分点。整体而言，使用ACO+POS-SVM比SVM总平均精度提高了4.8百分点，这说明使用ACO+POS-SVM算法优于传统的SVM算法。用ACO+POS-SVM识别效果最好为跌倒行为平均达到了93.4%，这是因为跌倒行为与其他行为相比，下降趋势更明显、速度更快、能量高度集中，所提取的MFCC向量也更容易识别。而跳跃和深蹲两个动作识别率比较低，分别是85.5%和86.3%，由于跳跃和深蹲两个动作都是相似的运动，跳跃动作自下而上，深蹲动作自上而下，而且维持的时间相似以及速度相当，故系统会出现误报情况。

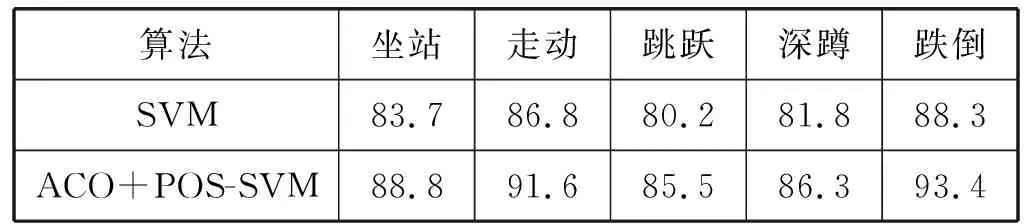
表1 算法对比(%)

3.2.2视距和非视距位置的性能分析

图9表示的是基于本文方法对会议室场景不同位置的五种行为的识别结果，其中，在视距条件下(位置1)，坐站、走动、跳跃、深蹲和跌倒平均识别结果分别为90.2%、93.9%、87.2%、88.4%和95.4%，在非视距(位置2和位置3)的行为识别结果会有所下降，但是走动和跌倒的识别结果都在90%以上。走动行为在五个行为里持续时间最长，跌倒行为速度最大，也使得这两个行为的识别结果较好。在视距情况下，只有一条直射路径，使得能量高度集中，相比于非视距情况而言，会有更加好的识别效果。在非视距状态下，实验采集了距发射机不同距离的两个位置，位置2和位置3的平均识别结果分别为88.3%和88%，实验结果表明，非常相似的行为坐站、跳跃和深蹲三个动作的识别结果都在88%以上，且在位置2和位置3的识别结果无明显差距。在实验中，位置2和位置3距离收发机的距离是有区别的，这也说明本文的识别方法在静态多径没有变化的情况下，如果仅仅由于位置发生了变化，识别效果不会下降太多，且在非视距的位置识别结果具有相似性。同时也说明了本文的识别方法对活动的人体行为识别具有一定的鲁棒性，对于实际情况而言，相比于其他只有视距情况的方法更具有实用性。

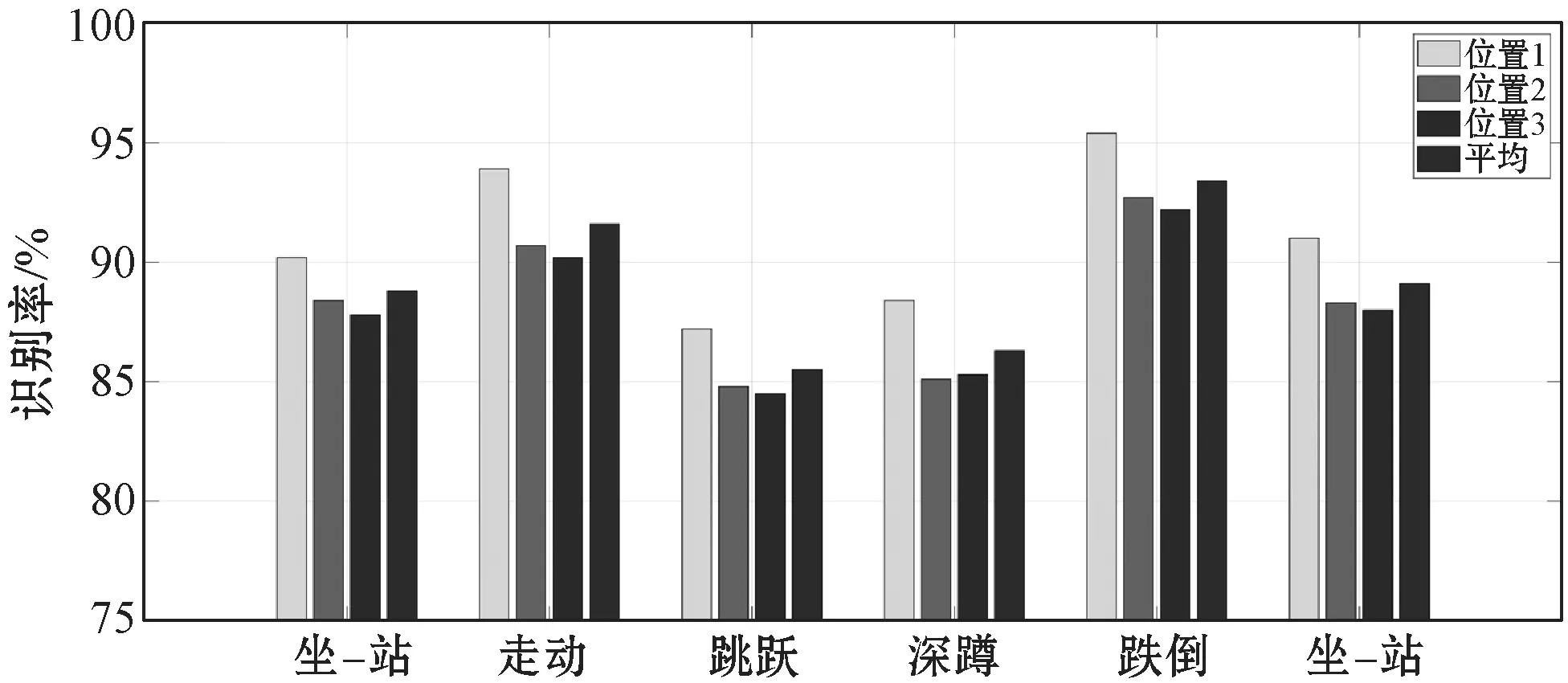
图9 位置识别结果对比

3.2.3特征对性能的影响

不同行为CSI信号的MFCC向量互不相同，因此可以将CSI信号的MFCC向量作为识别不同行为特征参量。为了提高分类的准确性，本文提出了使用MFCC向量的统计特征作为分类标准，分别是MFCC向量的均值、标准差和平均变化率作为分类特征量。图10为单用MFCC向量识别和用统计特征识别的结果。结果表明，用统计特征识别准确率分别提高3.8百分点、4.4百分点、4.8百分点、5.2百分点和4.7百分点。其中跳跃和深蹲动作提高明显，这说明了本文提出的基于MFCC向量的统计值比单独用MFCC向量识别具有一定的优越性。

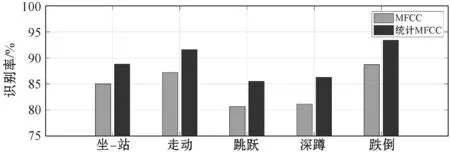
图10 统计特征对性能的影响

除了MFCC向量特征外，本文还额外增加了一个无偏移信号的对数频谱能量作为特征，图11表示的是此对数能量对整个识别结果的影响。对于总体数据而言，有对数能量的平均识别结果为89.1%，反之，识别结果仅为81.6%。增加了额外对数频谱能量特征，对于比较相似动作的区分是非常有用的。如图11所示，跳跃和深蹲动作的识别分别提升了7.4百分点和6.1百分点，这与2.2.2节的理论相符。跌倒动作在视距和非视距情况下平均识别效果可达93.4%。可见，增加无偏移信号的对数频谱能量特征给整体识别结果带来了提升，使系统更容易区分速度相似的动作。

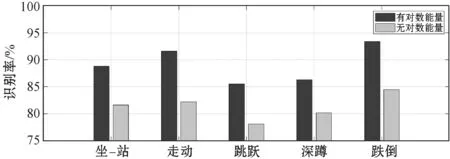
图11 有无对数能量性能对比

本文还将实验结果与时频特征和小波特征相进行了对比，如表2所示。结果表明，在预处理相同的前提下，本文方法均优于时频特征和小波特征识别结果。

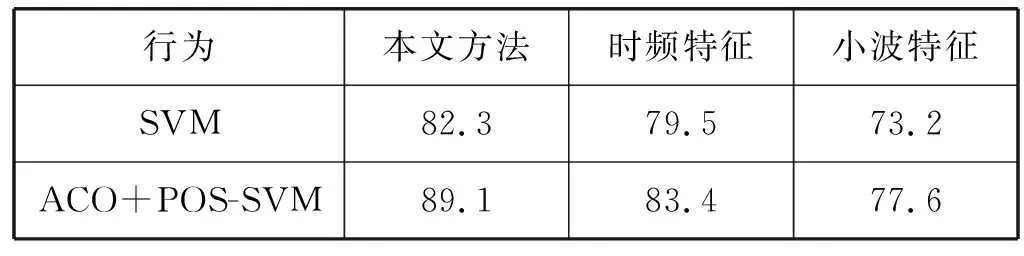
表2 方法对比(%)

4 结 语

本文参考了日常行为的CSI信号与语音信号传播的相似性以及共享带宽的性质，利用梅尔滤波器组能使低频率范围(0～10 kHz)的能量集中更加明显的特性，提出在CSI信号中提取MFCC向量统计特征作为识别日常人体行为识别方法。本文首先对数据做了滤波处理，论证了CSI信号流之间的相关性并用PCA对其处理，相位校准处理；然后在CSI中提取了MFCC向量统计特征和无相位偏移信号的对数频谱能量作为分类特征；最后用ACO+POS-SVM算法对在复杂场景下的视距和非视距情况的数据进行了识别，此方法对日常几个活动的分类达到了较好的效果。但是此实验中，识别的精度还有限，且仅考虑了一个人识别结果，这是比较局限的，未来的工作将会在实时活动识别、多人及更复杂的条件下推进，增加识别系统的广泛性与实用性。