基于预后验分析的边坡稳定监测风险决策方法
2023-01-30张浮平
张浮平,彭 兴
(长江勘测规划设计研究有限责任公司,湖北 武汉 430010)
0 引言
在岩土工程实践中不可避免的存在诸多不确定性因素,如有限数据导致的统计不确定性、岩土体力学参数的空间变异性、计算模型误差等[1]。岩土工程风险决策能够定量地考虑上述不确定性因素,是工程实践中重要的科学决策手段[2-5]。
以边坡工程风险分析为例,当根据计算参数的初始信息分析得到的边坡失效概率PF大于目标失效概率PT时,通常需要采取一定的加固措施来提高边坡的安全性,使边坡的失效概率小于目标失效概率。但工程师获得的初始信息往往有限,且存在较大的认知不确定性,据此采取的加固措施并不一定经济合理。另一方面,可通过布置监测仪器收集更多信息,以减小岩土体参数的认知不确定性,同样可以达到降低边坡失效概率的目的[6]。如果通过减小参数认知不确定性分析的边坡的失效概率小于目标失效概率,则无需对边坡采取加固措施,节省的加固措施费用可视为监测信息带来的效益,但获得监测信息同样需要增加额外的成本(如购买和安装监测仪器等)。对是否开展边坡安全监测进行风险决策是边坡加固设计中的一个重要问题,能够有效地避免盲目开展监测或者加固带来的不必要的成本。预后验分析(Pre-posterior analysis)能够有效地评估监测方案的潜在效益,科学指导监测方案的优化布设,被广泛应用于工程监测方案优化决策之中[7-9]。在预后验分析中,由于监测方案尚未实施,监测项目能够带来的潜在效益需要通过预测可能的监测结果和监测结果发生的概率(即预后验信息)计算监测项目信息价值的期望(Expected Value of Information,EVoI)来量化。在求解EVoI时,需要计算一系列可能监测结果所对应的边坡失效概率,即后验失效概率。常用的基于随机模拟的后验失效概率计算方法包括:马尔科夫链蒙特卡罗模拟[10]、基于结构可靠度的贝叶斯更新方法(Bayesian Updating with Structur⁃al reliability methods,BUS)[11]等。当上述方法应用于边坡稳定监测方案预后验分析时,对于不同的监测结果,通常需要重新执行随机模拟以求解对应的失效概率,由于边坡变形等监测项目的求解模型(如有限元计算模型、有限差分计算模型)比较复杂,计算效率低。因此如何高效地求解EVoI是边坡稳定监测方案预后验分析的一个关键难点,也是该方法难以运用于实际工程实践的重要制约因素之一。
本研究旨在建立基于预后验分析的边坡稳定监测方案风险决策模型,并将提出的改进拒绝抽样贝叶斯更新方法(Bayesian Updating with Structural reliability methods using Modified Rejection Sampling,BUS-MRS)应用到监测方案预后验分析中,以提高信息价值的计算效率。为此,本文首先介绍了边坡稳定监测方案预后验分析方法,随后介绍了基于BUSMRS 的信息价值计算方法和计算流程,最后用一个岩质边坡监测方案风险决策算例证明了所提方法的可行性和有效性。
1 边坡稳定监测预后验分析方法
1.1 监测方案的预后验分析模型
基于预后验分析的边坡稳定监测方案决策树如图1 所示。当根据初始信息判断边坡的失效概率PF大于目标失效概率PT时,则需判断是否需要获得额外的监测信息进行决策。在边坡监测方案风险决策中,首先需要确定可供选择的监测项目(如变形、孔隙水压等)Dk(k=1,2,…,q,q是监测项目的数量)。随后对监测项目可能的观测结果(即预后验信息)进行预估。监测项目Dk观测值的概率分布表示为f(dk),dk,l(l=1,2,…,Nk)为可能的观测结果。然后,通过贝叶斯更新方法计算观测结果dk,l对应的边坡后验失效概率PF(dk,l)。当后验失效概率PF(dk,l)>PT时,则仍需加固,总费用为监测费用Cm和加固费用Cr之和;当PF(dk,l)≤PT时,则不需要加固,总费用仅为监测费用Cm。随后,根据监测项目的可能观测结果dk的分布f(dk)和可能观测结果dk所对应的信息价值计算监测项目的EVoI。进行监测方案风险决策时,EVoI与监测费用Cm的关系也可以用信息价值比Vr=EVoI/Cm表征。当信息价值比Vr>1,表示监测信息产生的价值大于监测费用,可进行监测;当Vr≤1 时,监测费用大于监测产生的价值,则无需进行监测,应直接进行加固。

图1 基于预后验分析的边坡稳定监测方案决策树模型Fig.1 Decision tree model of slope stability monitoring scheme based on pre-posterior analysis
由此可见,基于预后验分析的监测方案风险决策中有两个比较关键的步骤:第一,确定监测项目的预后验信息,即观测结果的概率分布f(dk);第二,求解监测项目的EVoI。
1.2 监测项目的预后验信息f(dk)
预后验分析中需要对监测结果进行预估,即确定监测项目Dk的观测结果dk的分布f(dk)。预后验信息f(dk)可以根据工程师或专家的经验进行预测,也可以通过监测模型进行预测。当通过监测模型进行预测时,监测结果dk与边坡稳定性分析不确定性参数x之间的关系可表示为:

式中:εk为监测项目模型误差;Mk(x)为监测项目Dk的监测模型函数,表示输入参数和监测项目之间的响应关系。
在边坡稳定监测中,监测模型函数常为数值分析模型(如有限元模型、有限差分模型等)。因此,将不确定性参数(如摩擦角ϕ、黏聚力c和弹性模量E等)的初始分布f(x)的随机样本xl(l=1,2,…,Nk)为输入变量,通过监测模型函数Mk(x)计算样本对应监测模型的响应dk,l(l=1,2,…,Nk)。dk,l(l=1,2,…,Nk)服从分布f(dk),为监测项目的预后验信息。
1.3 监测项目信息价值的期望EVoI
在边坡稳定监测中,监测项目Dk的观测结果dk,l所产生的信息价值VoI为依据先验信息(即初始信息)做出决策的费用与根据监测结果dk,l做出决策的费用之差:
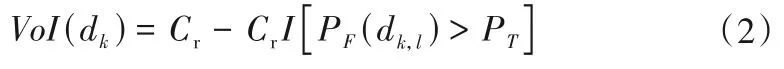
式中:I[ ]为示性函数,当PF(dk,l)>PT时,I[PF(dk,l)>PT]=1,即边坡仍然需要加固,监测信息带来的价值为0;当PF(dk,l)≤PT时,I[PF(dk,l)>PT]=0,即边坡无需加固,监测信息带来的价值为加固费用Cr。
预后验分析中需考虑所有可能的监测结果带来的价值,即监测项目信息价值的期望EVoI。根据贝叶斯理论,基于监测信息dk和参数先验信息f(x),可获得参数的后验概率密度函数为f(x|dk)。随后可根据不确定性参数的后验概率密度函数f(x|dk)计算边坡的后验失效概率PF(dk)。因此,基于MCS 根据预后验信息f(dk)计算监测项目Dk的EVoI可以表示为:
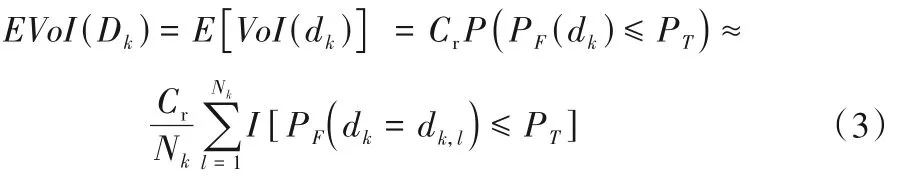
式中:P(PF(dk)≤PT)为获得监测结果后的后验失效概率小于目标失效概率的概率,表示监测后不需要加固的概率;dk,l(l=1,2,…,Nk)为监测变量dk的样本,代表可能出现的观测结果;Nk为样本的总数。
基于预后验分析的边坡稳定监测方案风险决策的一个难点是如何高效计算监测项目Dk的一系列可能的观测值dk,l(l=1,2,…,Nk)所对应的边坡后验失效概率PF(dk=dk,l)。为此,本文将BUS-MRS方法应用于预后验分析,以提高计算EVoI的效率。
2 基于BUS-MRS的预后验分析计算方法
2.1 基于结构可靠度的贝叶斯更新方法
Straub 和Papaioannou[11]提出了基于结构可靠度的贝叶斯更新方法BUS,将贝叶斯更新问题转化为可靠度求解问题,被扩展到求解贝叶斯更新中不确定性参数的后验分布。BUS 中构造的附加失效区域记为Ωl,表示给定观测值dl时监测模型函数对应的失效区域:

式中:cu是一个常数用于保证cuL(x|dl)≤1,可取1/L(x|dl)的最大值,即cu=;u是随机变量,服从0 到1 的均匀分布,且与模型不确定性参数x相互独立。初始分布f(x)的随机样本中落入到监测模型函数失效区域Ωl的样本(接受样本)服从后验分布f(x|dl)。换而言之,服从后验分布f(x|dl)的样本可以通过式(4)从先验分布f(x)的样本中选取。在拒绝抽样方法中,通过蒙特卡罗模拟(MCS)产生Nmcs个服从分布f(x)的样本xi(i=1,2,…,Nmcs)(即初始样本)和Nmcs个u的样本ui(i=1,2,…,Nmcs),如果ui≤cuL(xi|dl),样本xi落入到监测模型失效区域,并接受为d=dl的条件样本,记为xj。通过这种方式,Na,l(Na,l<Nmcs)个服从后验分布f(x|dl)的条件样本被选中。基于上述原始拒绝抽样(Ori⁃gnal Rejection Sampling,ORS)的贝叶斯更新方法产生后验分布f(x|dl)的条件样本xj(j=1,2,…,Na,l)可用于计算边坡的后验失效概率PF(d=dl):
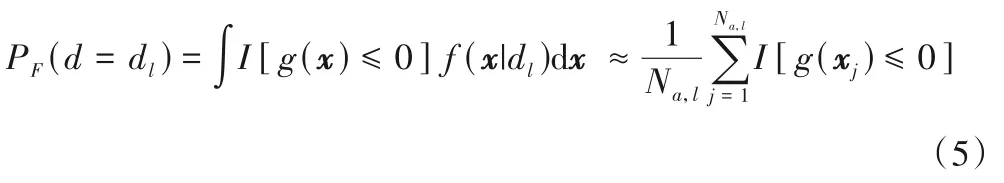
利用基于ORS 的贝叶斯更新方法计算边坡的后验失效概率需要根据不同的监测结果dl(l=1,2,…,Nd)重新执行MCS 产生初始样本再选择条件样本,然后根据条件样本计算边坡的后验失效概率。因此,在边坡监测方案风险决策中,需要对于Nd个观测结果需要执行Nd次MCS,那么总的计算量则包含Nmcs×Nd次监测模型函数M(x)和次功能函数g(x)的计算,可见计算量非常大,而且计算效率会随着监测模型函数和功能函数的求解复杂程度的增加而降低。
2.2 基于改进拒绝抽样的贝叶斯更新方法
为解决上述计算量大、计算效率低的问题,Li[12]等提出了基于改进拒绝抽样的贝叶斯更新方法(BUS-MRS),在拒绝抽样中从同一套初始样本中选择不同观测值dl所对应的条件样本。监测项目D的观测值dl变化后,似然函数的值会变化,条件样本也会变化,但初始样本x独立于dl,因此可从同一套初始样本中选择不同观测值dl对应的一套条件样本,避免了针对不同dl重复执行MCS 模拟产生新的初始样本和计算样本对应模型函数和功能函数的响应,从而提高了计算后验失效概率的效率。为了减少接受条件样本的随机波动,改进拒绝抽样(Modified Re⁃jection Sampling,MRS)通过在相同的初始样本空间中重新执行Nr次拒绝抽样以增加接受样本的数量,从而提高计算边坡后验失效概率的稳健性。在MRS中,每次运行拒绝抽样都产生一组服从后验概率密度函数f(x|dl)的条件样本Ωl,m(m=1,2,…..,Nr),则Nr次运行拒绝抽样获得条件样本的集合Ωall={Ωl,1,Ωl,2,…,Ωl,Nr}也服从后验概率密度函数f(x|dl)。采用BUS-MRS 计算后验失效概率PF(d=dl)可以表示为:

式中:xm,j是MRS 中第m(m=1,2,…..,Nr)次执行ORS 接受的样本;是第m次模拟中接受样本的数量;是MRS中接受条件样本的总数。在MRS 中,初始样本xi(i=1,2,…,Nmcs)在重复执行ORS中保持不变,样本xi是否会被接受将被Nr个ui判断Nr次,则初始样本xi被接受的次数从ORS 中的cuL(xi|dl)增加到MRS中的cuL(xi|dl)×Nr。随着Nr增加,xi被接受为条件样本的频数收敛于cuL(xi|dl)×Nr。因此,初始样本是否会被接受的随机波动在MRS 中会随着Nr的增大而减小。相应地,Ωall中的样本随着Nr的增加而增加,并收敛于条件样本数量的增加和条件样本随机波动的减少都有助于提高计算后验失效概率PF(d=dl)的稳健性。由于初始样本xi和其似然函数L(xi|dl)的响应是固定不变的,在Nr次运行ORS 中无需重新计算,MRS 方法重新执行ORS方法的计算量可以忽略不计。
2.3 基于BUS-MRS的信息价值计算方法
当利用BUS-MRS 计算监测项目的EVoI时,由于无需重新产生初始样本以及计算初始样本监测模型函数的响应,能够高效地求解监测项目一系列可能观测值所对应的后验失效概率,从而提高计算EVoI的效率。基于BUS-MRS计算给定监测项目Dk的观测结果dk,l条件下边坡的后验失效概率可以表示为PF(dk=dk,l):
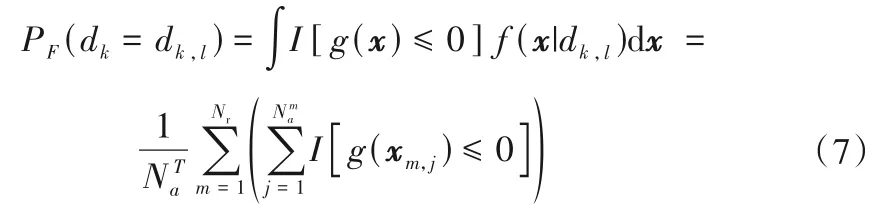
式中:xm,j是改进拒绝抽样中接受的样本;Nma是第m次接受样本的数量;NTa是接受的样本的总数。
将式(7)带入式(3),监测项目Dk信息价值的期望EVoI可以表示为:
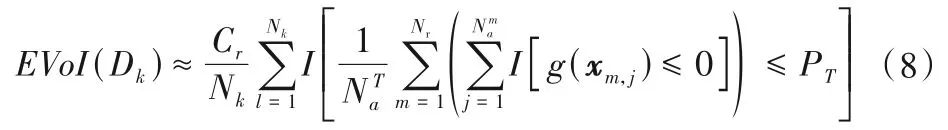
如图2所示,利用BUS-MRS方法进行边坡监测方案风险决策主要包括以下步骤:
图2 基于BUS-MRS的监测方案预后验分析计算流程图Fig.2 Implementation procedure of the proposed BUS-MRS based pre-posterior analysis
(1)利用MCS产生Nk个服从参数初始分布f(x)的样本xl(l=1,2,…,Nk);
(2)根据监测模型函数式(1)计算参数初始分布样本所对应的监测项目的观测结果dk,l,dk,l为服从预后验信息f(dk)的样本;
(3)根据BUS-MRS(即图2中的虚线方框部分)计算监测项目观测值dk,l(l=1,2,…,Nk)所对应的失效概率PF(dk=dk,l);
(4)根据式(8)计算监测项目的EVoI;
(5)重复上述步骤(2)~(4),直到计算完所有监测项目的EVoI;
(6)计算各个监测方案的信息价值比对监测方案进行决策。
在上述计算过程中,步骤(1)和步骤(3)中都需要利用不确定性参数初始分布f(x)的样本。由于在边坡监测方案中,监测模型复杂,为了节省计算量和计算时间,在实际计算过程中步骤(1)和步骤(3)可采用相同的样本。上述做法虽会产生一定的相关性,但是对EVoI计算结果的影响很小。
3 边坡稳定监测方案风险决策算例
3.1 边坡确定性分析模型
下面将以文献[13]中的岩质边坡为例说明本文方法的有效性。如图3 所示,岩质边坡高度为H=12 m,倾角60°,边坡内存在一条从坡脚开始以35°倾角向上延伸的结构面,在Z=4.35 m深处与垂直拉伸裂缝相交。张拉裂缝顶部与坡顶之间的距离为4 m。rw=Zw/Z表征地下水深度用比率。岩体黏聚力为67 kPa,摩擦角为40°,容重为26 kN/m3,弹性模量为5.0 GPa,泊松比为0.25。软弱结构面岩体的重度为γJ=26 kN/m3,泊松比为0.3。软弱结构面的弹性模量E、黏聚力c、摩擦角ϕ以及坡顶荷载p、地下水比率rw视为随机变量,其统计特征值和分布类型见表1。该边坡上施加了为4 排预应力锚杆,钢筋直径为28 mm,横、纵向间距均为2.5 m。锚杆与节理面法线的夹角为35°,深入节理面后的有效长度为4 m。锚杆杨氏模量为200 GPa、屈服应力为σt=400 MPa,锚杆的拉伸屈服力为246 kN。分别选取A、B、C、D 四个点(如图3 所示)的水平位移(即HA、HB、HC、HD)和竖直位移(VA、VB、VC、VD)为监测项目。
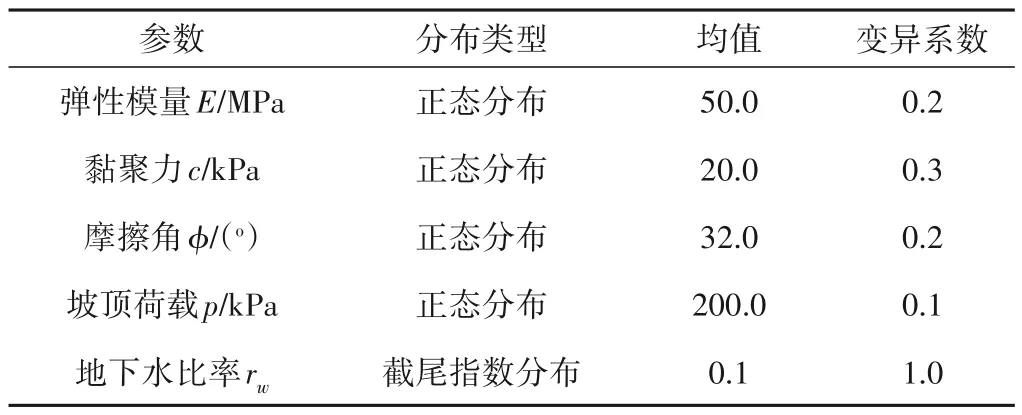
表1 岩质边坡的随机变量统计特征Tab.1 Statistics of random variables in the rock slope

图3 岩质边坡稳定性分析示意图Fig.3 Stability model for the rock slope
采用有限差分法分析软件FLAC 对岩质边坡稳定性进行分析,岩体和软弱结构面采用实体单元模拟,共有782 个单元,地下水用水位线Table 单元模拟,锚杆用Cable 单元模拟,采用理想弹塑性模型和摩尔-库伦屈服准则。需要指出,为了更好地和文献[13]进行对比,本文采用了与其保持一致的理想弹塑性模型,在具体工程中可以根据实际情况采用更合理的本构模型,并不影响本文提出的风险决策方法。采用强度折减法计算岩质边坡的安全系数,参数取均值时计算边坡位移如图4(a)所示,其中最大合位移约为7 mm,计算边坡抗滑稳定安全系数FS为1.14[图4(b)所示]。
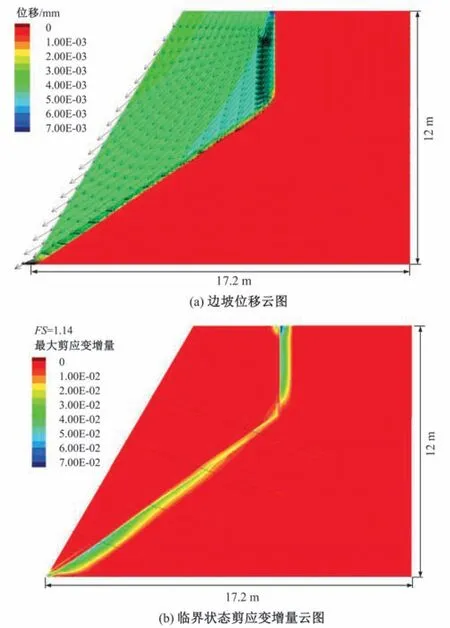
图4 有限差分模型计算岩质边坡的位移和安全系数Fig.4 Finite difference model for displacement and safety factor of the rock slope
本文采用非侵入式随机有限差分方法[14]对边坡稳定进行可靠度分析。计算过程如下,根据参数的初始分布(见表1),利用MATLAB 软件产生不确定性参数的随机样本,然后利用MATLAB 调用FLAC 软件逐一计算随机样本(即模型的输入参数)对应的边坡抗滑稳定安全系数FS,最后在MATLAB 中进行可靠度分析。假定FS计算的模型误差εg服从均值为0、标准差为0.05 的正态分布。边坡稳定分析的功能函数为g(x)=FS(x)-1+εg。根据表1 参数的初始分布利用MCS 方法(样本数为1.5万个)计算边坡的失效概率为25.5%,与文献[13]计算的失效概率24.9%相近。
该边坡的规模较小,边坡目标失效概率可取PT=1%。根据参数的初始信息计算边坡稳定的初始失效概率为PF=25.5%大于目标失效概率,不满足设计要求,需在原设计方案基础上对边坡进行加固。在此,考虑是否对边坡进行监测,然后再做是否加固的决策。为此,本文考虑以4 个监测点A、B、C、D 的水平位移(HA、HB、HC、HD)和竖直位移(VA、VB、VC、VD)等8 个监测项目进行监测方案的预后验分析。加固费用和监测费用的比例为Fr=Cr/Cm,由于该算例为并非实际工程,在此假设Fr=100。
3.2 预后验决策分析
在预后验分析中,首先需要确定监测项目的预后验信息。此算例中通过参数的初始分布和监测模型函数对监测结果进行估计。其具体计算过程如下,首先根据参数的初始分布(见表1)产生1.5 万个样本,然后利用非侵入式随机有限差分方法调用FLAC 位移计算模型(即监测模型)分别自动求解1.5 万个样本在A、B、C、D 的水平和竖直方向的位移。每个监测变量可以获得1.5 万个监测位移值,这1.5 万个监测值即为监测位移预后验分布的等效样本,用于代表监测位移的预后验信息。
确定预后验信息后,需计算预后验信息的样本(即监测项目的观测值)所对应的后验失效概率。图5给出了所提的BUSMRS方法计算HB不同观测值所对应的后验失效概率。可见,边坡的后验失效概率随着HB值的增加增长了近3 个数量级,表明边坡开挖后的监测项目的位移越大,边坡的安全性越低。BUSMRS 中考虑Nr分别取1、10 和100 的3 种情况,3 种情况的计算结果较为一致。当Nr=1 时,即原始拒绝抽样,计算后验失效概率的离散性比较大,尤其是在失效概率较小的区域(如<10-2)。随着Nr从1 增加到100,后验失效概率计算结果基本趋于稳定。证明改进拒绝抽样方法通过在初始样本空间重复选择监测结果对应的条件样本,能够提高计算后验失效概率的稳健性。

图5 监测位移HB不同观测值的后验失效概率Fig.5 Posterior failure probabilities with different monitoring displacement
根据监测的可能观测结果和观测结果对应的失效概率,可以计算信息价值的期望。本算例采用信息价值比Vr=EVoI/Cm表征监测项目的潜在收益。图6 给出了8 个监测项目的信息价值比。可见所有监测项目的Vr都大于1,因此对任何一个监测项目实施监测获得的信息价值都大于监测的成本。在这8个监测项目中,HB对应的Vr最大,因此对坡脚水平位移HB进行监测在信息价值的角度上最为合理。
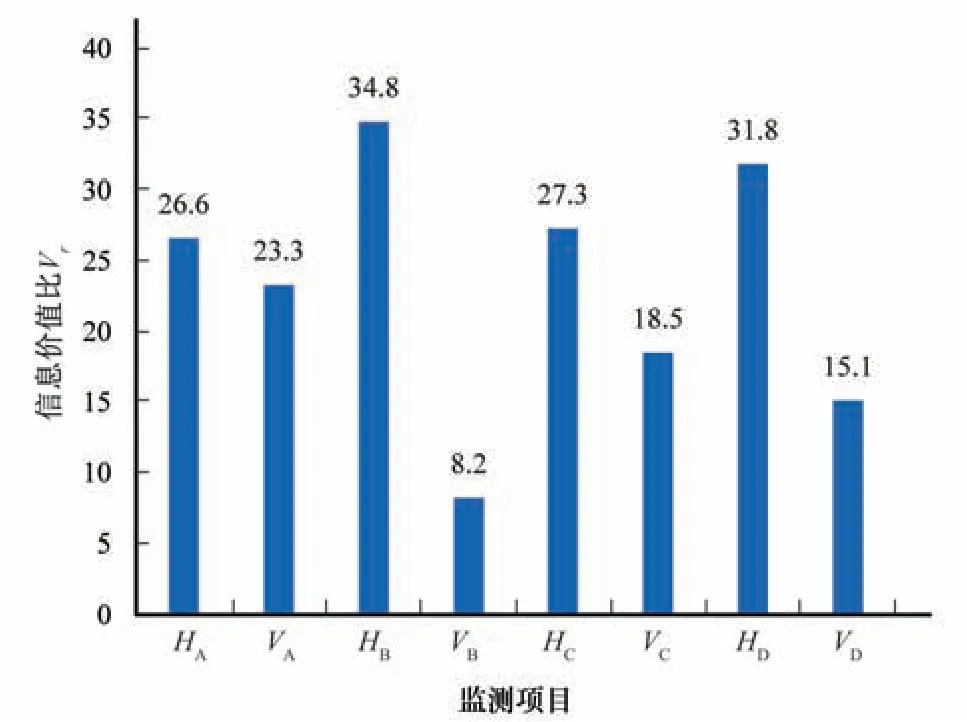
图6 不同监测项目的信息价值比Fig.6 EVoI for different monitoring parameters
4 结论
本文建立了基于预后验分析的边坡稳定监测风险决策模型。针对预后验分析中信息价值计算效率低的问题,提出的基于改进拒绝抽样贝叶斯更新方法BUS-MRS 的能够有效提高监测项目信息价值期望的计算效率。主要结论如下:
(1)在预后验分析中,BUS-MRS 能够高效地计算监测项目一系列可能观测值的后验失效概率,提高了基于预后验分析的边坡监测方案风险决策方法的实用性和适用性。
(2)岩质边坡监测算例表明,所提方法能够有效地识别最大信息价值对应的最优监测方案,从信息价值的角度为边坡监测方案的优化决策提供了新思路。算例中对坡脚的水平位移监测能够获得最大的信息价值。
