水轮机转子系统动力学参数在轨辨识方法

陈 俊，钟 智，薛建中，赵云峰，平金伟，肖 亮

（1.南京南瑞继保工程技术有限公司，江苏 南京 211002；2.华能澜沧江水电股份有限公司，云南 昆明 650214；3.西安热工研究院有限公司，陕西 西安 710054）

0 引言

水轮机是把水力资源转换为电能最常用的设备，是水力发电领域重要的基础设备；确保水轮机安全稳定运行对水力发电过程有重要影响。水轮机转子系统是水轮机中的核心部分，研究水轮机组转子系统的稳定性对于提高整个机组的运行安全有非常重要的意义；而正确辨识水轮机转子系统动力学参数是研究转子系统可靠性、稳定性的关键。

目前，国内外学者在水轮机转子系统动力学参数辨识方面进行了不少研究。吴鹏飞等［1］基于粒子群算法实现了电磁式振动能量采集器参数的辨识，这种辨识方法通过传递矩阵法精准、自由地判断与采集待辨识的动力学参数；但传递矩阵法下的参数是随时变化的，根据参数的变化量来确定最终的算法量，能够减小动力学参数因为维度的不同而产生的数据偏差较大的问题。黄梦华等［2］基于旋转坐标系给出了零序分量条件下的瞬时功率计算方法，这种方法根据瞬时功率的功率变化而采集动力学参数，进而制定辨识算法；该方法具有较好的辨识适应能力，但存在精度较低的问题。黄光斌等［3］结合智能算法建立了VSG 工频信号模型，在模型中采集控制参数；根据小信号的变化特征分析动力学参数的稳定性，辨识结果以功率模式体现。

以上三种辨识方法均需要大量借助外部的动力学参数以及功率识别设备与算法，只有硬件结构达标和软件计算程序应用熟练的背景下才能够较好地实现。为了解决水轮机转子系统动力学参数辨识中存在的精度低、稳定性差等问题，结合动力学参数特征和水轮机转子系统的基础参数进行了在轨辨识方法的研究，验证了在轨辨识方法的适应能力和精准度。

1 水轮机转子系统动力学参数的建模

1.1 参数特性

水轮机在水中的振动特性主要是由两个激振力共同引起的，一个是水轮机本身的不平衡力，另一个是水轮机在水中受到的水流激振力［4］。因此，识别水轮机转子系统动力学参数特征即是识别水轮机的各个结构部位的激励特征参数。水轮机系统在工作过程中产生弯曲状态下的振动方程可以表示为［5］：

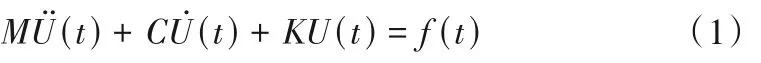
式中：M为水轮机转子质量矩阵；为加速度；C为阻尼矩阵；为速度；K为刚度矩阵；U(t)为位移；f（t）为所受外部不平衡力。

水轮机转子在工作的过程中会不断受到外部水流的力学作用，主要包括水轮机转子自身受到的不平衡力和水流对外的横向力［6］。其中，不平衡力是由于旋转轴在旋转的过程中发生位置变动所致；产生的旋转力将会使旋转轴处于不平衡状态，由不平衡状态导致的周期性不平衡力采用如下公式进行计算：

式中：m为质量；ω为角速度；e为周期。

1.2 水轮机转子有限元模型

基于欧拉伯努利梁理论，建立了水轮机转子上的柔性轴有限元模型，水轮机转子系统整体的有限元模型如图1 所示。模型不仅可以体现水轮机转子系统中一切结构的动力学参数，还能够对离散分布的轴承结构元件进行定位分析，将动力学的计算参数对应到相应的结构上［7，8］。在模型中沿着水轮机转子的中心线划分，明晰了主要结构部件与轴承、铁芯等工作轨之间的位置距离参数。

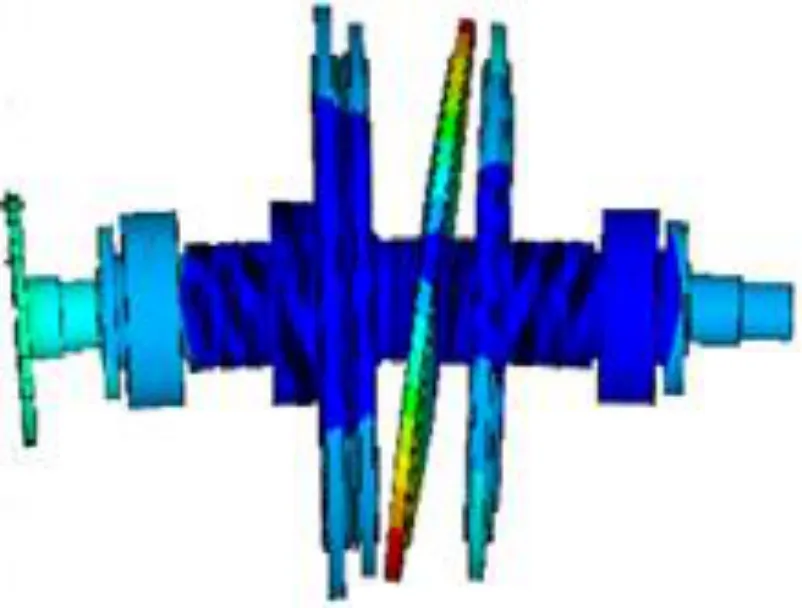
图1 水轮机转子系统整体的有限元模型Fig.1 The finite element mode of hydraulic turbine rotor system

单一的通过有限元模型并不能清晰获取动力学参数的详细信息［9］，还需要有水轮机转子系统的平面示意图来作为辅助。在平面示意图上需要建立一个坐标系，其原则是以转子系统的中轴作为转子运动的轨道中心，具体表现方式如图2所示。

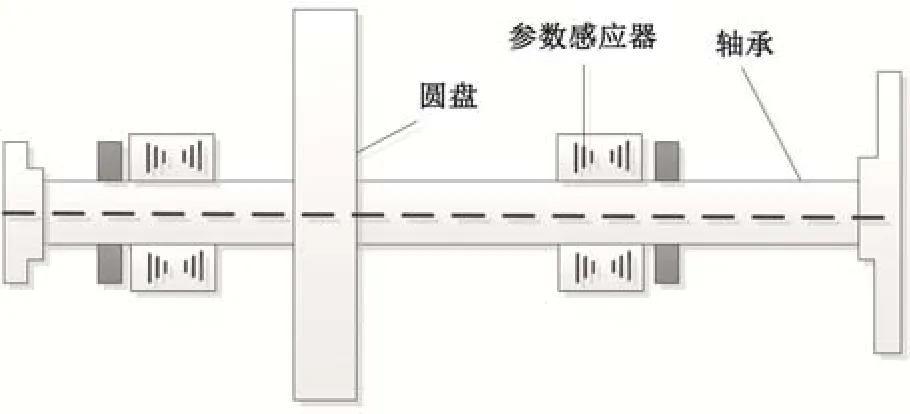
图2 水轮机转子系统平面示意图Fig.2 Plane figure of hydraulic turbine rotor system

根据平面图中的位置状态，确定转子工作的运动状态可以分为平行移动方式和转动方式［10］，两种运动状态均是在轨道上正常运行的；其中，平行运动状态是以横坐标为基准，转动运动状态是以纵坐标轴为基准。每次发生角度转动均会绕轴旋转明确的角度，在角度的基础上进一步确定转矩的大小，利用横截面在坐标轴上的位移量来对动力学相关参数精准分析。

水轮机转子整体运行时需要根据不同动作性质的部件进行节点划分，每个确定的节点在转轴中均需要一个可以反复的位移向量系数，该系数可以采用欧拉伯努利梁理论进行计算：

式中：x为横向位移；y为纵向位移；θ为水轮机转子在坐标轴上的旋转角度；j为节点。

1.3 水轮机转子轴承、盘轴参数模型

水轮机转子轴承平面示意图如图3 所示，其参数模型中动力学参数的形成主要是由于电磁铁为转子提供方向相反的作用力，不同作用时间下的轴承自由度不同，实时产生微小电流变化。水轮机转子轴承工作电流发生变化时，转子自身结构中的电磁线圈电流并不会发生太大的改变，会主动控制转子在平衡的位置。

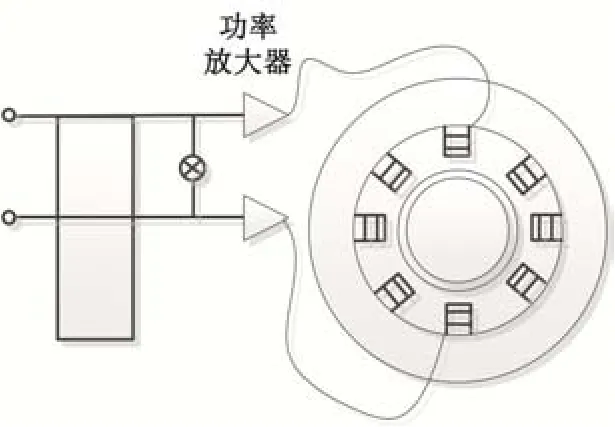
图3 水轮机转子轴承平面示意图Fig.3 Plane figure of hydraulic turbine rotor bearing

根据图3 中水轮机转子轴承的动作原理可知，由电磁轴承控制的转子动力学参数是由常系数决定的；而常系数主要包括线圈匝数和电磁导通率等。对这些常系数进行线性化处理可以得到更加精确的动力学参数，步骤为：对电磁轴承中的支撑力进行提取，利用电磁正常导通情况下的稳定电流，采用线性化处理方式得到轴承对转子的支撑力：

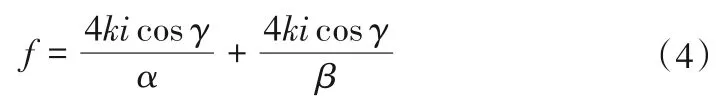
式中：f为轴承对转子的支撑力；k为刚度系数；i为电流常数；α、β分别为转子的动作位移角度。

广汽集团近几年快速发展，从合资合作起步，到自主品牌突破。广汽集团于2017年宣布成立广汽新能源公司，专注于新能源汽车研发、制造和销售。新工厂落成后，广汽基于全新开发的纯电动专属平台生产的新能源汽车将快速推向市场。今年以来，广汽新能源作为新能源汽车行业的后起之秀爆发出惊人的增长力，最新数据显示，广汽新能源11月销量首次突破三千达3104台，同比增长307%；今年1-11月累计销量达16945台，同比增长294%，大大超越行业68%的平均水平，而且提前一个月超额完成全年1.5万台销量目标，全年有望达到2万台。

盘轴参数模型中可以提取的动力学参数主要是在转子圆盘与转轴之间的角度变化过程中选择。圆盘与转轴之间一直存在相对平衡的角度关系；且圆盘与转轴之间还存在阻尼弹性关系，阻尼的大小将直接影响转子相对运动角度。用坐标轴方法来描述转子的运动角度，则可以设定圆盘正处于坐标轴中心，圆盘的外角度也可以作为水轮机转子系统的运动轨道。

盘轴的基本转动单元可以看作转子系统动作的基本运动轨道，在轨道上不断产生转动惯量，从而转换成为动力学参数。

2 动力学参数在轨辨识

2.1 辨识常用方法

频域辨识法是水轮机转子系统动力学参数辨识常用方法之一，该方法可以直接对动力学参数进行代号编码，根据编码特征寻找水轮机转子系统中的时域信号，将时域信号转换成频域信号即可提取出来动力学参数值；但该方法对动力学参数中的周期性敏感［11］。在实际的频域参数辨识方法下需要营造一个稳定的并网环境，随机生成一个激励信号，由该激励信号进入输出环节中，确定动力学参数的周期和信号码宽；并且这种方法还需要由多个辨识环节共同参与，很难从单一的水轮机转子系统中提取完整的动力学参数。

动力学参数辨识法是水轮机转子系统动力学参数辨识另一常用方法，该方法能够对参数采集节点中的所有数据进行函数计算，利用多重积分估计原理模拟动力学参数对外表达形式。时域辨识方法最终对外输出的参数结果是依靠曲线形式的，但是水轮机转子系统中的动力学参数具有多样性，无法通过曲线形式实现精准表达。

针对频域辨识法和时域辨识法的不足，智能算法下的参数辨识法由于具有多个算法（采用遗传算法），且每个算法均可以对动力学参数进行分析，能够解决动力学参数的非线性问题，最终的辨识结果也相对于时域法、频域法更加标准。但是智能算法下的参数辨识法灵活性较低，只能对设定的参数进行识别。

2.2 参数辨识整体策略

水轮机转子系统在运行的过程中是处于实时动态的，为高效完成水轮机转子系统的动力学参数轨道辨识，将最小二乘法应用到参数辨识整体策略研究中。最小二乘法可以将转子系统中的轨道固定动力学参数转换成为二阶模型，通过二阶模型对动力学参数实时模拟。在二阶模型中有两种线性变化特征，两种特征之间相互依存，保证转子系统的参数离散型始终处于线性的连续状态。经过最小二乘法推算后得到的轨道固定参数识别模型为：

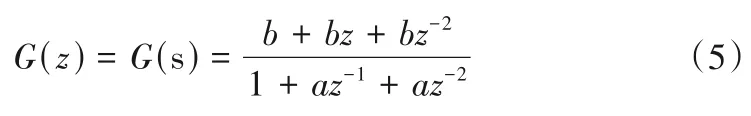
式中：a为x 方向轨待识别参数；b为y 方向轨待识别参数；z为z方向轨待识别参数；s为双线性模型中可变化系数。

在该模型中进行在轨参数辨识还需要其他函数的配合，辨识精度越高的参数需要的其他函数数据量也就越多。因此，本研究在已有的模型中引用递推算法，不断更新最小二乘法中的数据类型。递推算法具有无矩阵特点，不需要将已经计算出的数据进行储存，可以满足待辨识参数的实时提取与分析。

2.3 辨识结果的误差分析

在轨动力学参数辨识结果误差产生的原因主要是非线性模型基础数据不稳定，以及水轮机转子系统功率不稳定两种因素。非线性模型中具有两条线性变化方式，每条线性变化方式都拥有独自的工作频率，在进行在轨参数辨识的过程中没有固定的端电压与工作频率统一节点，会使转子系统中产生的动力学参数发生微小变化。

水轮机转子系统中的内轨动力学参数可以通过对电流环的控制来自适应辨识模块。为了突出辨识结果的误差从而寻找到最佳的辨识方法，使用VSG 控制方式对水轮机转子系统中的供应电流精细化，观察微小的电流变化。电流的变化会带动电压、阻抗的变化，当水轮机转子系统在被辨识的过程中电压发生较大起伏，则会产生误差；系统工作功率变化对误差大小的影响如图4 所示。为了减少误差值，对系统中的辨识算法增加线性系统模型，寻找误差点与精准点之间的平衡量：

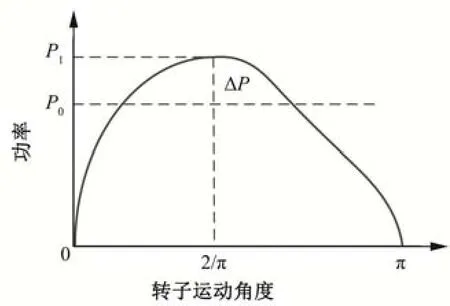
图4 功率变化引起的误差变化Fig.4 Error changes caused by power changes

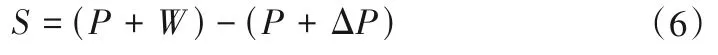
式中：S为误差与精准点之间的平衡值；P为系统平衡状态下的功率；W为外部输入功率；∆P为系统工作功率扰动量。

3 实验研究

基于上文中提到的相关算法和辨识误差分析结果，本实验采用了动力学参数采集，建立较为精准的非线性模型，同时利用最小二乘法建立一个二阶的稳定模型，保证水轮机转子系统在工作的过程中产生的变化动力学参数能够被辨识算法实时记录。在轨辨识方法首先确定水轮机正常工作状态下的机组流量，确保流量可以改变动力学参数；然后规划出有效流量对转子系统所做的功。设定水轮机转子系统中的圆盘结构即为在轨辨识方法中的假定轨道，从圆盘结构中获取相关动力学参数完成辨识方法流程。圆盘结构正常运转下的机械功率与其他功率之间可以看作是可替代关系，为了验证本研究的在轨辨识方法，还将瞬时功率计算辨识方法、电磁轴辨识方法应用到水轮机转子系统中，共同提取、辨识动力学参数。

实验中分别控制瞬时功率计算辨识方法、电磁轴辨识方法及在轨辨识方法的辨识时间、额定功率取值范围、基础常数以及机械功率等内容，最终将3 种方法的辨识结果以适应度的形式体现出来。不断迭代3种方法的辨识结果，使适应度稳定，得到最优值。3种方法对动力学参数的识别适应度对比结果如图5 所示。由图5 可知，在轨辨识方法经过相同次数的算法迭代后，适应度趋于稳定，并逐渐与动力学参数相适应。而瞬时功率计算辨识方法的适应度最终的算法迭代结果只能保持在0.2左右，电磁轴辨识方法的算法迭代结果保持在0.15左右。

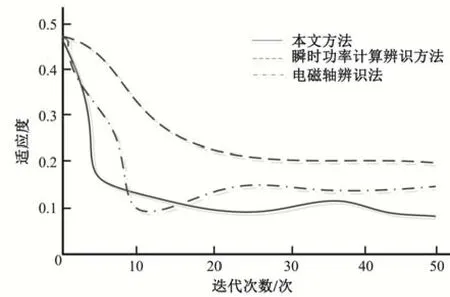
图5 辨识方法适应度对比结果Fig.5 Comparison results of fitness of identification methods

实验中对3 种方法的辨识误差进行了对比，结果如图6 所示。由图6 可知，本研究采用的在轨辨识方法的误差在±0.5 MW 范围内，而瞬时功率计算辨识方法和电磁轴辨识法的误差均在±0.8 MW范围内。产生差异的主要原因是由于在轨辨识方法对于转子系统中的动力学参数识别具有更好的精准性和收敛性，而且还具有多个模型共同参与在轨辨识方法的实施，在轨辨识方法的运行流程是始终基于圆盘结构上的，外部的其他力学因素无法干扰辨识结果。

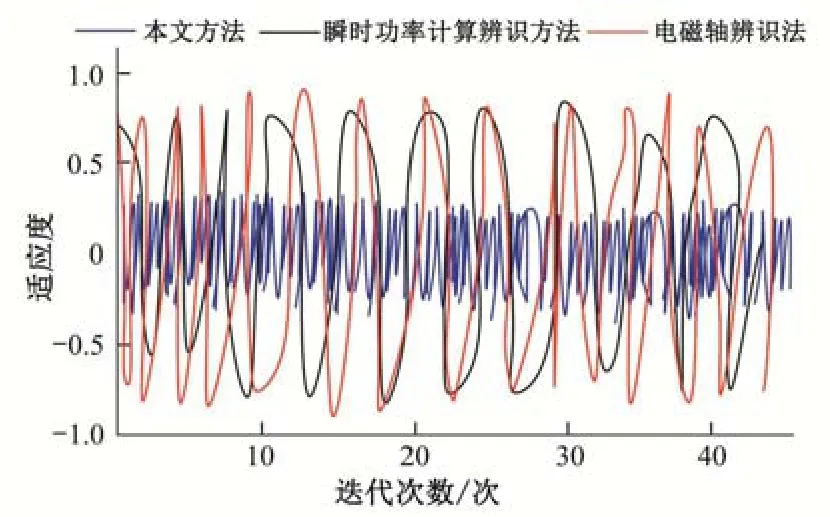
图6 3种方法的辨识误差对比结果Fig.6 Recognizing error comparison between three methods

4 结语

本研究选用在轨辨识法对水轮机转子系统的动力学参数进行了精准辨识，同时对水轮机转子系统的动力学参数真实性、稳定性进行了验证，明确了水轮机转子系统的工作参数特性。但水轮机转子系统动力学参数辨识方法的运用细节，如在轨辨识方法的实施流程、算法应用到动力学参数的各个项目中等内容，没有被深入探讨，有待在将来研究中进一步开展。