基于分形插值与支持向量机混合模型的大坝变形分析
2023-01-30向亚红邓念武谢雨航
向亚红,张 峰,邓念武,谢雨航
(1.湖北省防汛抗旱机动抢险总队,湖北 武汉 430064;2.武汉大学水利水电学院,湖北 武汉 430072)
0 引言
大坝变形受到库水位、温度和时效等多种环境量因素的影响[1],为研究大坝变形规律,了解大坝变形状态,对大坝运行过程中可能出现的异常状况作好应急准备,需要通过建立数学分析模型,对大坝变形规律和变形趋势进行认识和掌握。许多学者应用神经网络[2,3]、遗传算法[4]、支持向量机[5]等方法,以及两种或两种以上预测方法联合建立的混合模型[6-9]对大坝变形进行了研究和分析,这些方法主要是通过建立变形量与环境变量之间的映射关系对大坝变形进行分析和研究。
大坝变形监测数据属于时间序列,监测数据具有随机性、多尺度变化等复杂的特性,分形理论可以有效识别时间序列隐含的内在规律。Su 等[10]应用多重分形去趋势波动分析法对某混凝土重力坝现场观测数据进行分析,确定了现有大坝时间序列的多重分形标度行为,刻画了大坝的长期行为和结构演变规律;周兰庭等[11,12]利用分形理论解析了大坝变形性态的多重分形特征及其对称性;利用多重分形理论对混凝土重力坝水平位移的波动进行了分析,指出位移多重分形特征受到环境量影响明显。胡江等[13]利用多重分形去趋势波动方法从局部和整体两个方面对大坝的工作性态及演变规律进行了评价。大坝变形时间序列具有多重分形的特征,可以根据大坝的自相似性应用分形插值方法对大坝变形时间序列进行分析和预测。进一步研究表明,在构造分形插值拟合时,由于拟合出的图形是分数维的,不可避免地会出现断裂或周期现象[14];在构造分形插值外延预测模型时,对均方偏差最小的点进行搜索时需要较长的计算时间,且预测点距离已知序列越远,预测误差会越大。针对上述问题,本文尝试引入支持向量机(SVM)对分形插值方法进行优化,从而获取更优的拟合和预测模型。
1 分形插值算法
分形插值算法是将分析数据的复杂性与数据本身可规律化结合起来,来预测数据的走向、数据值与区间值,以便获得相关成果并进行应用[15]。数据的属性具有不确定性和复杂性,分形插值通过已知数据点之间的关系,学习和分析潜在规律并进行自相似性延拓,经过多次仿射系统迭代,可大大缩小样本数据预测值与实测数据之间的差距,从而避免固定形式函数图像偏离实测数据而引起的较大误差[16]。
对于一个时间序列数据,根据分形插值理论,建立时间序列点集{(xi,Yi),i=1,2,…,N},(xi为时间或序列值,Yi为测值)。对时间序列点集按照公式(1)进行标准化处理。得到标准化点集{(xi,yi),i=1,2,…,N}。
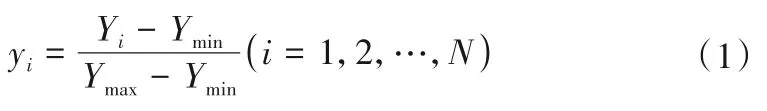
式中:Ymax为最大值;Ymin为最小值。
根据分形插值理论可知,可以构造一个R2上的迭代函数系(IFS),使它的吸引子G恰好是点集{(xi,yi)|i=1,2,...N}的连续函数f:[x0,xn]→R上的图形上。该迭代函数系为:
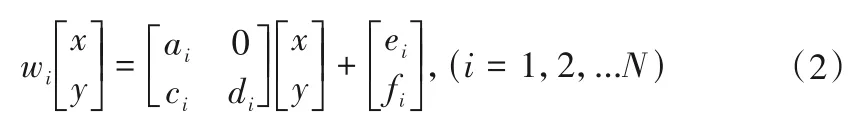
且上式满足端点条件:
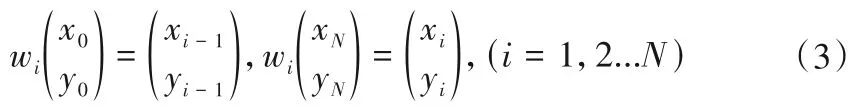
式中:wi为待求的仿射变换矩阵;ai、ci、di、ei、fi为仿射变换参数,具体算法如下:

其中垂直比例因子di是关键参数,di的计算方法有几何法、经验估计、平均值法等,为了兼顾数据的整体和局部的特性,更好地体现数据的分形特征,提高分形插值的拟合精度,结合大坝水平位移序列特点,本文采用随机因子法[如式(5)]计算垂直比例因子di。
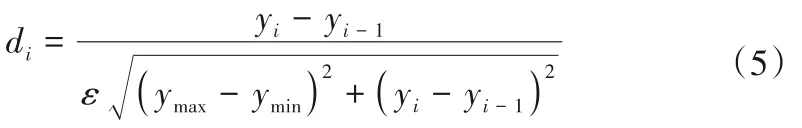
式中:ymax、ymin是指以待插值点为中心前后扩展n0个点区间中的最大和最小值;ε=1 +rand(1),rand(1)表示随机函数,代表一个0 到1 之间的随机数。由yi、yi-1体现局部信息,ymax、ymin体现全局信息,随机数保证了分形本身的特性。
根据上述原理即可以求出所有变换矩阵wi,将初始迭代点(本文选择时间序列第一个点)带入公式(2),不断迭代吸引子,最后得出插值点集组成的时间序列曲线。
2 支持向量机(SVM)算法
设训练样本集为:{(xi,yi),i=1,2,…,N},xi∈Rd为输入特征向量[5,16],在大坝监测数据中为影响因子;yi∈{ -1,1}为标准化后的数据,即算法的评判指标,在大坝监测数据中为效应量。支持向量机需要通过已知样本对函数关系式(6)进行训练,以便找到输入特征向量和评判指标间的最优关系。
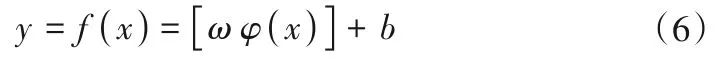
为了解决输入特征向量和评判指标间的非线性关系,需要将其映射到高维空间转化为线性问题。式中ω为分类超平面的权值,b为分类超平面的偏值。
该模型的优化问题为:
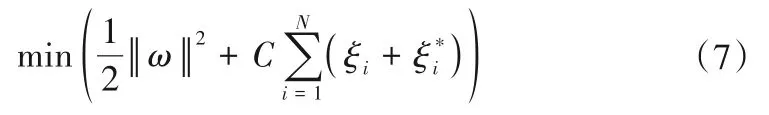
约束条件为:
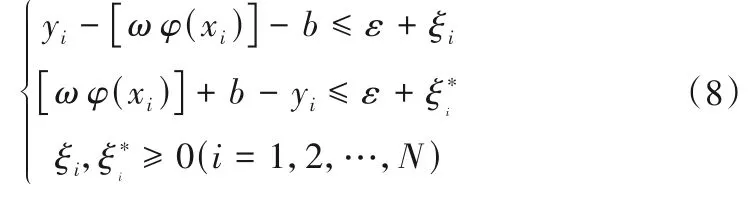
式中:ξi为松弛变量;C为惩罚参数;ε为估计精度,f(xi)与yi的差别小于ε时不计入误差,大于ε时误差记为|f(xi)-yi|-ε。
利用拉格朗日函数求解,考虑非线性可分情况,并引入用核函数K(x,xi),得到最优超平面的决策函数:

式中:αi,αi*为拉格朗日算子。核函数K(x,xi)是支持向量机的关键函数。目前研究中最常用的核函数主要有径向基核函数(RBF)、多项式核函数和Sigmoid 核函数3 种。径向基核函数中只有一个参数r,该核函数能够较好地反映模型选择的复杂度。研究表明:选择合适的参数后,径向基核函数可以适用于大坝变形序列的样本。鉴于此,本文核函数采用径向基核函数,如公式(10)所示。
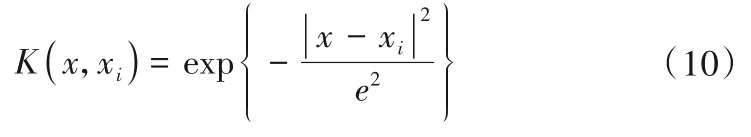
要构造一个具有较高预测精度的支持向量机模型,必须进行模型参数寻优来选择合适的模型参数。模型参数优化的主要思想是将目标函数极小化,使得模型预测值和实际观测数据之间能够达到最佳的拟合效果。鉴于大坝变形时间序列本身的复杂性,常规优化算法往往难以满足参数优化的目的。本文采取交叉验证(Cross Validation,CV)方法来进行模型参数寻优。交叉验证是一种统计方法,它可以用来验证分类器的性能,交叉验证法的基本思想是将原始数据序列分成两组,其中一组序列称为训练集,另一组序列称为测试集。首先用训练集对计算模型进行训练,通过训练学习开展参数寻优,得到最优的模型参数,建立预测模型,然后用该模型对测试集进行预测,最后用测试集的计算结果来对该模型进行效果评价。
3 基于分形插值与支持向量机的大坝变形混合模型
基于分形插值和支持向量机的大坝变形混合模型首先是通过对时间序列的分析,找出所有满足要求的特征点,对特征点集和原始点集通过分形插值算法得到位移时间序列插值点集,然后利用支持向量机对分形插值得到的曲线通过参数寻优,得到优化后的拟合曲线。
利用支持向量机理论预测下一个特征点,通过分形插值按照前面的方法进行迭代,计算插值点,最后再利用支持向量机进行参数寻优,得到预测曲线。其步骤如下:
(1)建立时间序列点集:选取各观测点位移时间序列,并进行标准化处理,得到时间序列{(xi,yi),i=1,2,…,N},利用分形检验指标和重标极差分析法(Rescaled Range Analysis,R/S)[12]进行序列分析,判断其分形特征性质。
(2)建立时间序列曲线的迭代函数系(IFS):根据公式(4)和(5)分别计算初始仿射变换参数ai、ei、ci、fi,和垂直比例因子di,构造迭代函数系(IFS)。
(3)根据仿射变换系,以时间序列的第一个点作为初始迭代点,计算初始吸引子,通过迭代拟合该测点的最优位移时间序列曲线。
(4)根据基础数据和位移时间序列曲线,利用支持向量机构造一个具有更高拟合精度的SVM拟合曲线。
(5)根据上述拟合曲线及插值点集,利用支持向量机算法预测最近的一个特征点值。
(6)利用新的插值点集,重复(2)~(5)步,构造新的位移时间序列曲线,步骤(4)最后的拟合值至本步骤最后的预测值间的位移时间序列曲线即为预测曲线。
(7)如此反复,直至计算出所有预测数据。
4 工程实例
以某混凝土重力坝159 m 高程廊道中水平位移实测数据为例,建立基于分形插值和支持向量机的混合模型分析大坝变形。该坝159 m高程廊道内顺河向水平位移观测方法为引张线法,在8~35 坝段分别布设一个测点,共28 个测点,引张线两端点(7 坝段和36 坝段)布置垂线组,以便计算引张线各测点的绝对水平位移。引张线观测方法采用自动化观测,以往下游变形为正,往上游变形为负。本文选取8 号测点2006 年1 月至2015年6 月共85 期数据进行分析。前79 期数据建立模型并检验拟合精度,后6期用来检验模型预测精度。
4.1 监测数据分形分析
利用分形检验指标计算8号测点水平位移时间序列偏度和峰度,结果表明:该测点时间序列偏度为-0.519,说明其时间序列数据分布有左侧长尾;该测点时间序列峰度为0.278,说明观测点水平位移时间序列的整体分布比正态分布高。总体来看,该测点表现为“胖尾”状的非正态分布,测点位移时间序列具有自相似性、可相加性以及非连续性等分形特征。
运用重标极差分析法(Rescaled Range Analysis,R/S)[17]计算8 号测点的Hurst指数为0.625,大于0.5 的评判标准。拟合相关系数为0.973,拟合相关系数大于0.9 的评判标准,说明监测点未来的位移变化趋势与过去的位移变化趋势一致,存在正的长程相关性。即在上一段时间内,由于荷载变化(如水位、温度等发生变化)引起大坝向上游(或下游)移动,在下一个段时间内相同效应变化则会导致大坝向相同方向移动。
综合分析表明:8号测点水平位移时间序列具有分形特征,可以利用分形插值方法对其进行分析。
4.2 分形插值与支持向量机混合模型拟合分析
基于MATLAB R2014a 和LIBSVM 软件平台编写分形插值与支持向量机混合模型,在各自阶段的参数寻优和曲线拟合的基础上,经过多次迭代,得到最佳拟合曲线。
图1 为8 号测点分形插值拟合图,图2 为8 号测点基于支持向量机和分形插值的混合模型拟合图。观测数据表明:大坝在水位、温度和时效因素的多重影响下,呈现明显的周期变化,上述两种拟合方法都明显反映了这种变化规律。但基于支持向量机和分形插值的混合模型拟合精度更高。
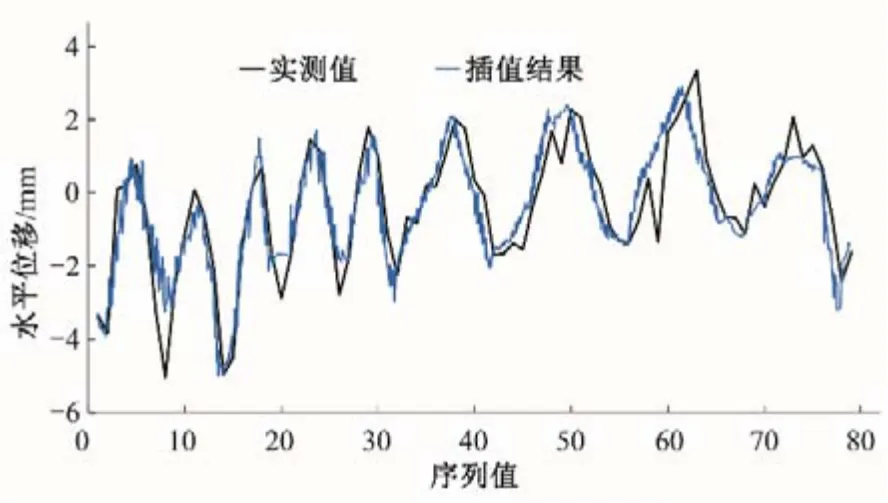
图1 8号测点分形插值拟合图Fig.1 No 8 fractal interpolation Model fit curve

图2 8号测点混合模型拟合图Fig.2 No 8 Hybrid Model fit curve
为了进一步比较模型的精度,引入均方根误差RMSE进行评判。
均方根误差公式为:
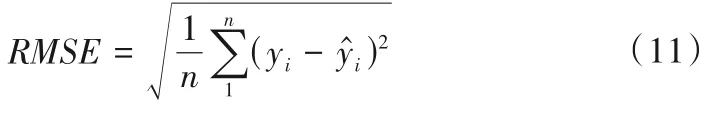
式中:yi为实测值模型计算值;n为数据序列数。
计算表明:分形插值模型的RMSE为0.94,分形插值与支持向量机混合模型的RMSE为0.90。
综合分析可知,在进行分形插值拟合后,运用支持向量机对数据进行优化,在各测点水平位移时间序列拟合中可以取得更好的效果,混合模型的拟合精度比单独使用分形插值模型拟合效果更好。
4.3 分形插值与支持向量机混合模型预测分析
对2015年的前6个月测值进行预测。8号测点预测时间段内实测值,以及混合模型、分形插值模型和SVM 模型的预测值和残差见表1所示。
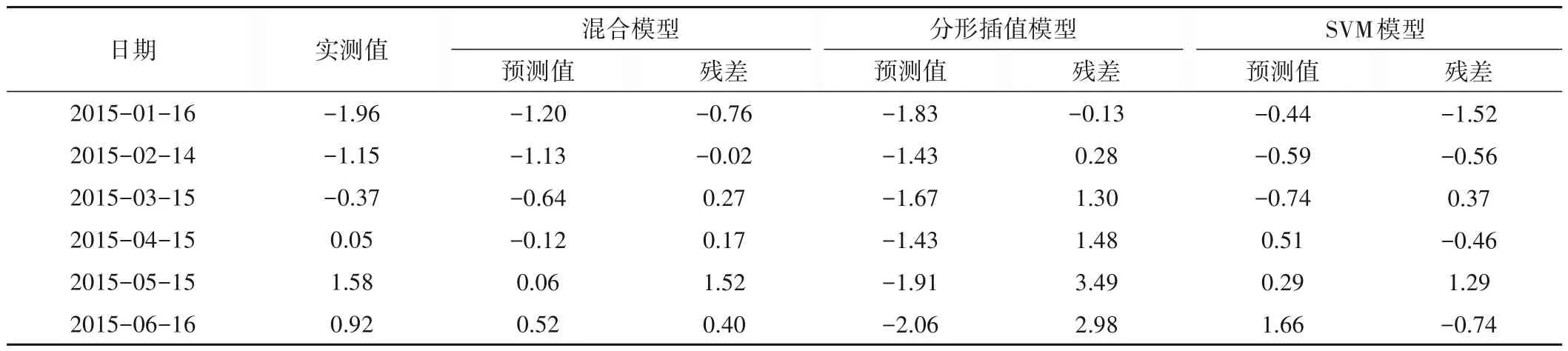
表1 8号测点预测时间段内的实测值、预测值和残差表 mmTab.1 observation,predictive values and residual error of No.8
由表1可知,在进行分形插值预测时,预测点距离已知序列越远,预测误差会越大,说明其外延预测范围有限。这三种模型中混合模型预测精度最高。2015 年5 月15 日的预测值不太理想,通过实测数据规律分析,该期数据很可能有粗差的影响。
为了进一步分析分形插值与支持向量机混合模型外延预测效果,分别计算出混合模型、分形插值模型、支持向量机模型的残差均方根RMSE分别为0.72、2.04、0.93。
计算结果可知,在进行位移时间序列预测时,分形插值与支持向量机混合模型的预测精度要高于单一模型,混合模型在工程实例中得到了较成功的应用。
5 结论
针对利用分形插值理论建立大坝位移时间序列模型过程中,预测效率较低、预测序列越长精度越差等缺点,提出了应用支持向量机算法对分形插值模型进行优化。结合大坝变形时间序列特点,通过垂直比例因子和核函数的选择,建立了基于分形插值与支持向量机大坝变形混合模型。
结合工程实例采用分形插值与支持向量机混合模型对某大坝水平位移进行了拟合和预测分析,结果表明:利用支持向量机优化的分形插值模型拟合精度高于分形插值模型;混合模型预测精度也高于分形插值模型和支持向量机模型。分形插值与支持向量机混合模型在大坝变形分析研究中取得较好的效果。
