基于CFD 的底部上翘角度对直管式出水流道水流性能的影响研究

孙晨光，王芳芳，高 昂，罗 洁，陆伟刚

（1.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，江苏 南京 210029；2.扬州大学，江苏 扬州 225009）

0 引言

泵站出水流道前承水泵导叶体，后启泵站出水池，其作用是削减导叶出口水流旋转能量，最大程度地回收水流的动能。低扬程泵站的出水流道设计形式主要包括直管式、虹吸式和箱涵式等，其中直管式出水流道结构简单，运行维护方便，广泛应用于平原地区河网工程的低扬程泵站［1-4］，其水力性能优劣对泵站运行效率及安全起着至关重要的影响［5，6］。在泵站设计过程中，当水泵安装高程低于出水池高程时，可以考虑采用底部上翘的直管式出水流道以减少开挖量。关于底部上翘式出水流道设计并没有专门的规范指导，因此为确保出水流道设计的合理性，研究底部上翘角度对直管式出水流道水力性能的影响是十分必要的，研究成果对底部上翘式出水流道设计具有重要的参考意义。近年来国内外的很多专家学者采用数值模拟［7-10］和物模试验［11-15］等方法开展了上翘式出水流道水流性能研究。颜红勤等［16］采用CFD 软件探讨了不同型线设计对上翘式出水流道水力性能的影响，结果表明渐变段长度对上翘式出水流道的水力损失和内流流态有着决定性影响，渐变段越长，出水流道的水力性能越优异；周亚军等［17］基于CFD 软件对竖井贯流泵装置进行了全流道定常数值模拟，对比分析了平直管式和底部上翘式出水流道的水力性能，结果表明出水流道底部上翘角对出水流道综合性能和工程土建投资存在影响；针对斜式轴流泵出水流道长期存在的偏流问题，王本宏等［18］采用数值模拟方法，阐释了偏流形成的机理；颜士开［19］采用数值模拟和物模试验方法揭示了出水流道偏流的主要原因，并提出增设导流板能够有效抑制偏流；谢丽华等［20］针对我国新引进的斜15°轴流泵装置进行了水动力特性试验，试验结果表明叶片角度较小时，泵装置空化特性较优，压力脉动相较常规立式轴流泵为大，出水流道流量分布不均；徐磊等［21，22］采用Fluent 软件对大型斜式泵装置进行了数值模拟，提出了改变导流板形式、延长中隔墩长度等优化措施，对出水流道偏流情况进行纠正，改善了出水流道两侧水流分布不均的情况；陆伟刚等［23］采用物理模型试验方法，验证了竖井式进水流道和底部上翘式出水流道的水力性能，预测了泵站实际运行的综合性能，结果表明该泵站的能量性能、汽蚀性能及飞逸特性良好，压力脉动在合理范围内。

目前关于上翘式出水流道的研究方向主要集中在内流纠偏和型线调整，研究内容主要为出水流道的水力损失、压力脉动［24］等基础水力性能指标，对于底部上翘式出水流道的关注不足，缺乏对底部上翘角度影响的研究。因此本研究从底部上翘式出水流道切入，以通吕运河大型低扬程泵装置为例［25］，进行数值模拟，基于流道内流流态、水力性能指标、涡通量及流速均匀度的沿程分布特性，展开出水流道底部上翘角度的影响分析。由于直管式出水流道结构简单，流道体型设计类同，因此研究成果具有一定的代表性，对低扬程泵站工程的直管式出水流道设计具有借鉴作用。

1 研究对象与方法

1.1 研究对象

本研究以通吕运河大型低扬程泵装置为例，泵装置立面图示于图1，平面图示于图2。该泵装置设计流量为100 m³/s，设计扬程为1.98 m，装配贯流泵机组3 台套，单泵设计流量Qn=33.3 m³/s，采用TJ04-ZL-07 号水力模型，叶轮直径Dn=3.3 m，转速nn=108 r/min。泵装置采用竖井式进水流道和直管式出水流道，顺水流方向总长为38.8 m。

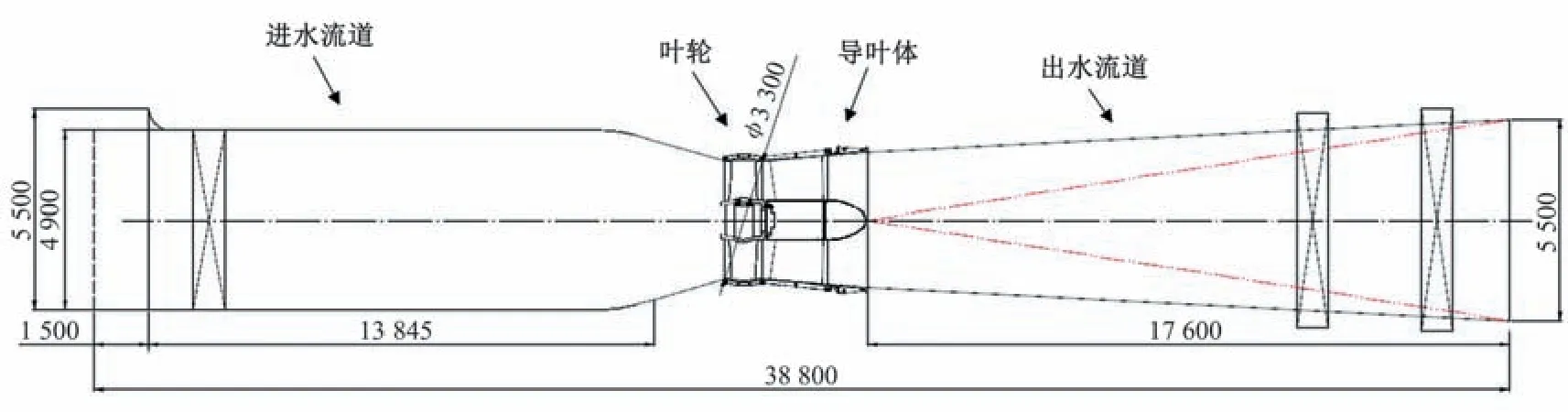
图1 泵装置立面图（单位：mm）Fig.1 Pump unit elevation

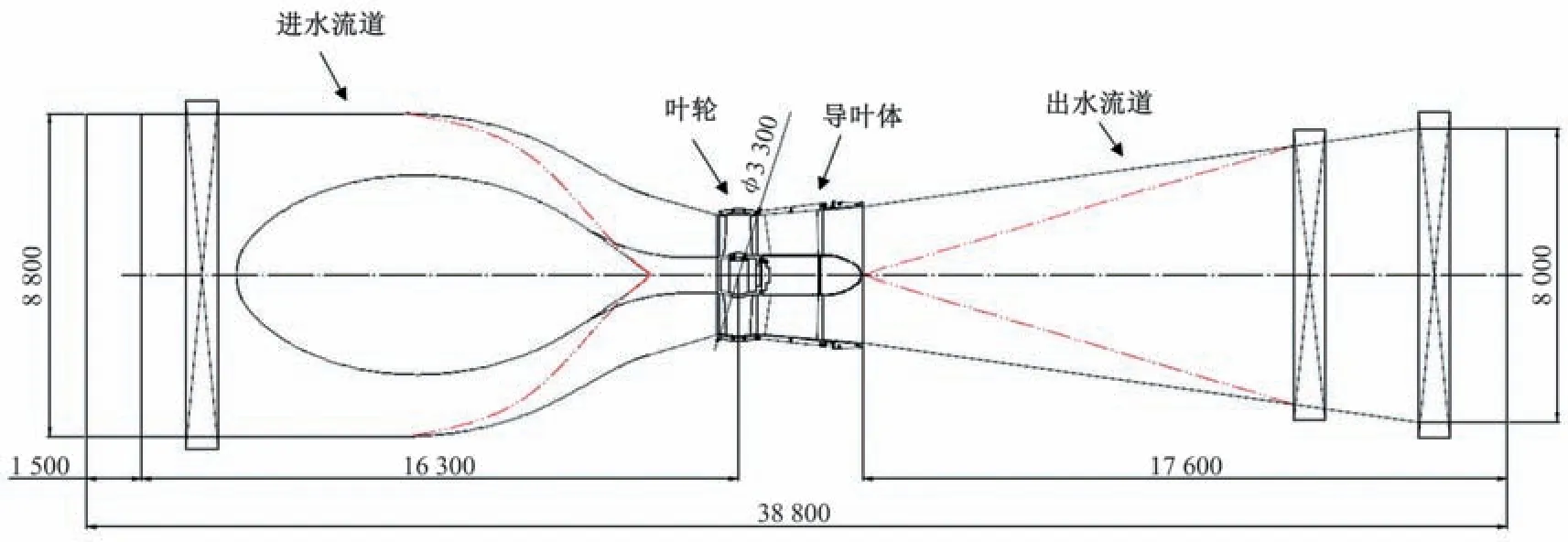
图2 泵装置平面图（单位：mm）Fig.2 Pump unit ichnography

1.2 研究方法

泵装置内部流场为三维不可压缩黏性湍流流动，控制方程采用连续性方程和Navier-Stokes 方程，由于不可压缩湍流流动的热交换非常有限，因此不予考虑［26-28］。

数值模拟采用ANSYS CFX 19.2软件求解方程组，选择能够更好地处理高曲率及大旋转流动的RNGk-ε模型使控制方程封闭。

RNGk-ε模型的湍动能k方程与耗散率ε方程可以写为［29］：

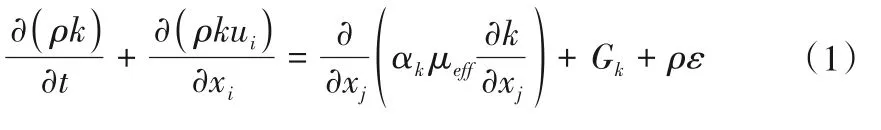
2 数值计算前处理

2.1 计算域设计

为方便数值计算结果与模型试验结果进行对比，以几何比尺Lr=11 建立计算域示于图3。如图3 所示，顺水流流动方向依次为进水池、进水流道、叶轮、导叶体、出水流道及出水池，进水池和出水池的长度设置为10 倍的模型叶轮直径，即10Dm，以保证水流稳定充分地流动。

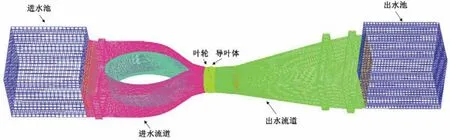
图3 模型泵装置计算域Fig.3 Model pump device computational domain

模型泵装置采用单台套贯流泵机组，设计流量的换算公式为：

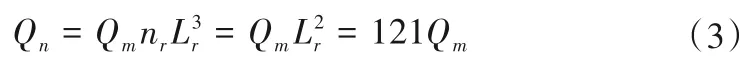
式中：下标r为原模型泵装置的比值；Qm为模型单泵设计流量，m3/s；Qn为原型单泵设计流量，m3/s。

2.2 网格划分及无关性分析

基于ICEM CFD 19.2软件的分块拓扑网格技术对计算域进行网格划分，网格类型为六面体结构化网格，ICEM 进、出水流道网格质量均在0.5 以上，叶轮和导叶体网格质量均大于0.2，模型泵装置中各部件y+值均大于20，能够满足选用RNGk-ε模型进行数值计算的要求。各过流部件结构化网格示于图4，各部件网格数量及节点数量如表1所示。

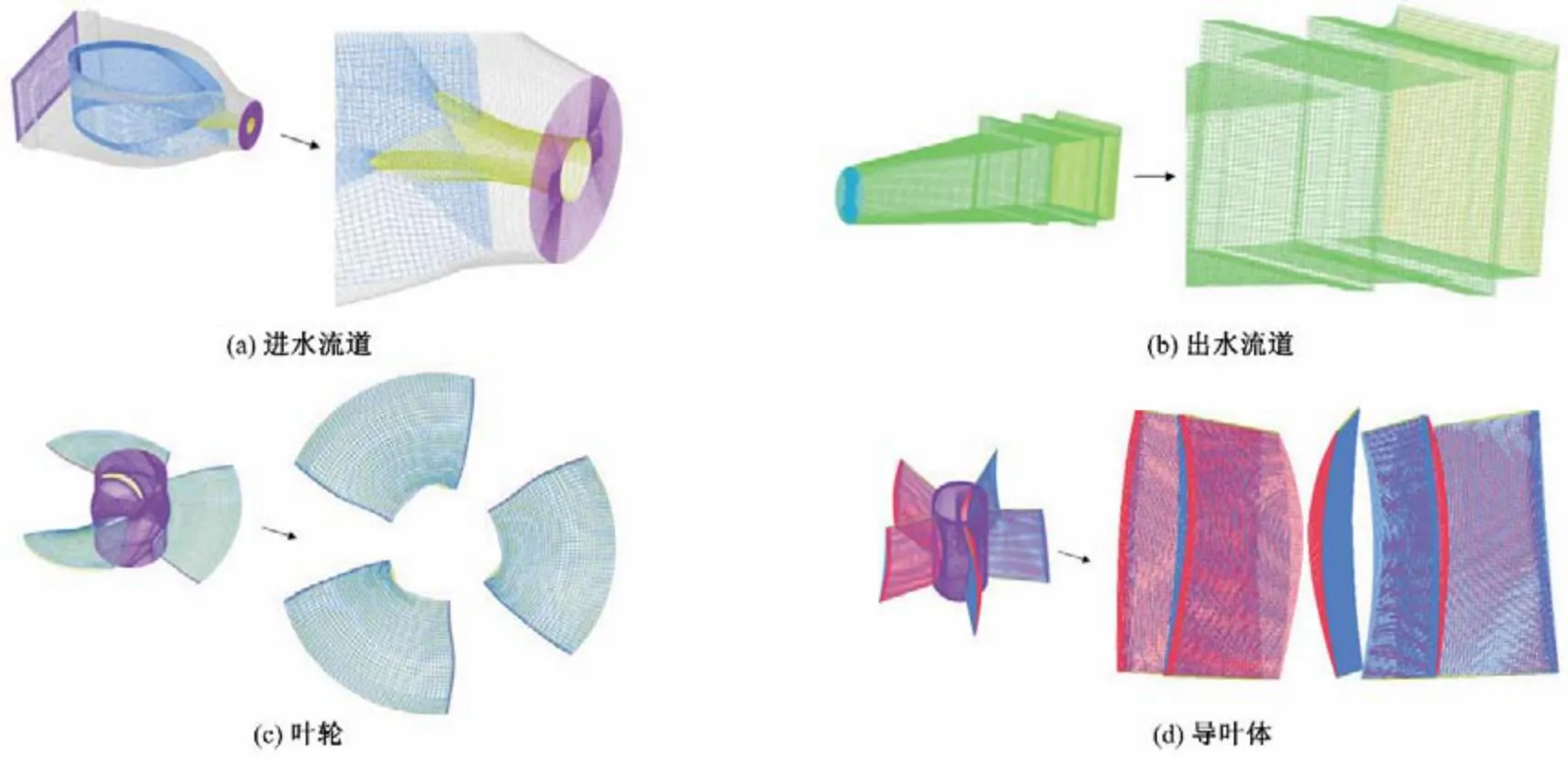
图4 主要过流部件网格Fig.4 Grid of main overcurrent components

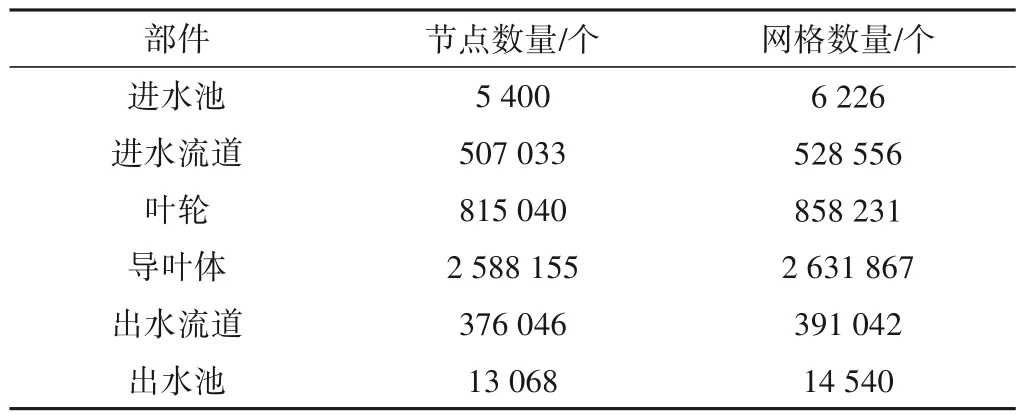
表1 泵装置过流部件网格Tab.1 Pump unit wetted parts grid

选取叶片角度为0°、设计流量Qm工况下的泵装置模型进行网格无关性分析，结果如图5 所示。由图5 可知，当总网格数大于443 万个时，泵装置扬程变化相对误差小于1%，综合考虑计算效率和精度，采用网格总数为443 万个的结构化网格进行数值计算，能够满足网格无关性要求。

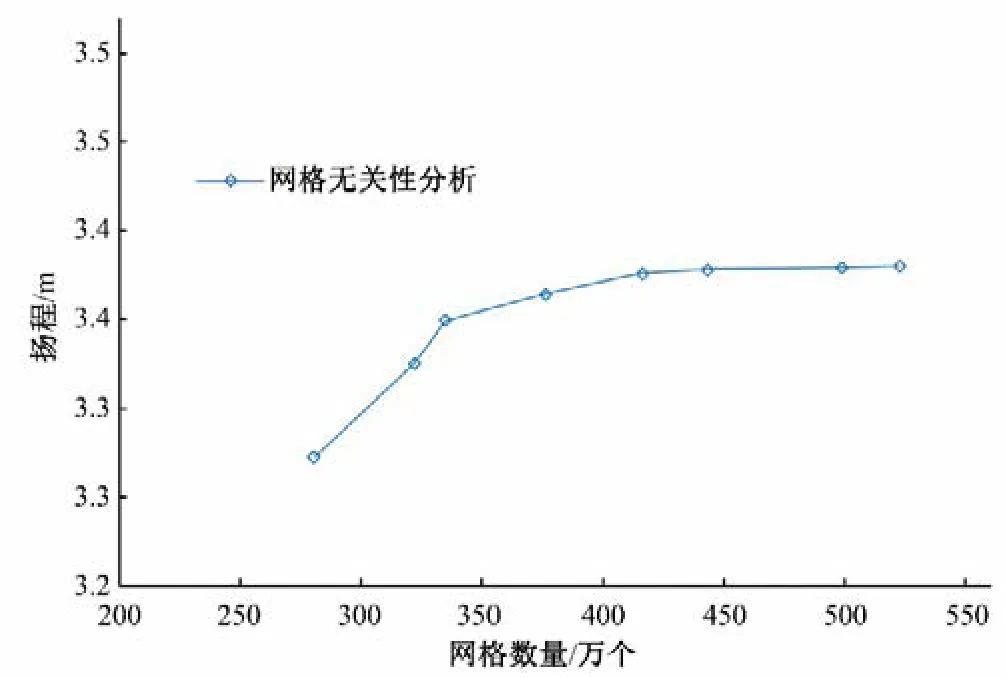
图5 网格无关性分析Fig.5 Mesh Independence Analysis

2.3 边界条件

模型泵装置数值计算的进口边界设置为进水池进口断面，该断面距离进水流道进口断面足够远，因此可以认为该断面流速为均匀分布，进口边界条件设置为“Total Pressure”，压力设为0.101 MPa（1 个标准大气压）；出口边界设置为出水池出口断面，能够保证出水流道出口断面后部水流充分发展，出口边界条件设置为“Mass Flow Rate”，流量值设置为设计流量Qm；进水流道、出水流道、叶轮室、导叶室边壁及进出水池底壁均设置为静止壁面，选用无滑移条件“Wall”，近壁面采用可伸缩壁面函数；叶轮部分设置为旋转域，转速为额定转速nm，泵装置其余部分设置为静止域。采用“Stage”交界面传递动静交界面之间动静耦合的流动参数［30，31］，除动静交界面外其他的交界面，即静静交界面，均采用“None”形式。

2.4 数模—物模试验外特性验证

在扬州大学高精度泵站试验台对模型泵装置进行物理模型试验，得到其试验外特性曲线［23，25］。泵装置模型照片如图6所示。

图6 泵装置模型试验现场照片Fig.6 Pumping unit model test

对模型泵装置进行数值计算，得到其计算外特性曲线。将试验、计算外特性曲线绘制于图7。由图7 可见，数值模拟计算的工况为Qm=0.295、0.285、0.275、0.265、0.255 m3/s，针对数值模拟的5 种计算工况，对模型试验数据进行插值得到同工况下的扬程、效率值。数据比对后发现，泵装置扬程的差值在0.1 m 以内，泵装置效率的差值在2%以内。数值模拟与模型试验的外特性曲线较为接近且具有相同的变化趋势，故认为数值模拟所采用的计算方法能够准确地模拟泵装置的内流流动，有效保证计算结果的可靠性。

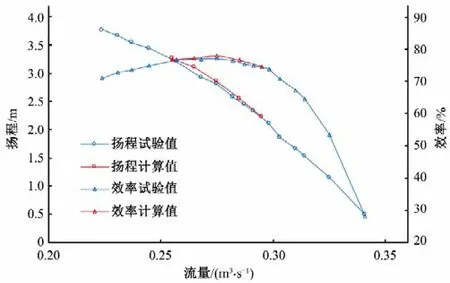
图7 数值模拟与模型试验外特性比较Fig.7 Comparison of external characteristics between numerical simulation and model test

3 结果与分析

3.1 水力性能指标

为定量衡量出水流道的水力性能，采用泵装置效率、出水流道水力损失作为基础水力性能指标，引入压力恢复系数反映出水流道的动能回收情况，两相结合评价出水流道的水力性能。

（1）泵装置效率。泵装置效率为输入轴功率与输出轴功率的比值，其计算公式为：

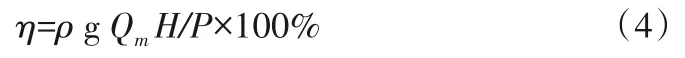
式中：η为泵装置效率，%；ρ为流体密度，g/cm3；g为重力加速度，m/s2；H为泵装置扬程，m；P为输入轴功率，kW。

（2）出水流道水力损失。基于伯努利方程，水力损失的计算公式为：

式中：h为出水流道水力损失，m；Pout为出水流道进、出口断面总压之差，Pa。

（3）压力恢复系数。压能为断面的压力势能，其数值为压力与液体重度的比值。压力恢复系数ζ定义为出水流道出口断面压能与进口断面压能的比值，数值越接近100%，出水流道的动能回收率越高。压力恢复系数的计算公式为：

式中：ζ为压力恢复系数，%；Eout为出水流道出口压能，m；Ein为出水流道进口压能，m。

3.2 底部水平式出水流道水力性能分析

出水流道底部上翘角度如图8 所示，原方案出水流道为底部水平式，θ=0°。图9 为θ=0°设计工况下的出水流道流场图。由图9可知，设计流量工况高速区主要集中在叶轮段，流出叶轮段后流速迅速降低，在出水流道中后段流速逐渐趋于稳定；叶轮段水流流线为逆时针偏转，与叶轮转动的方向一致，水流经过导叶调整后流线的弯曲程度降低，但在出水流道前部仍存在紊乱流线，该部分紊乱流线延续至出水流道中后部，出水流道后部水流经过扩散调整流线逐渐顺直，直至出口断面。

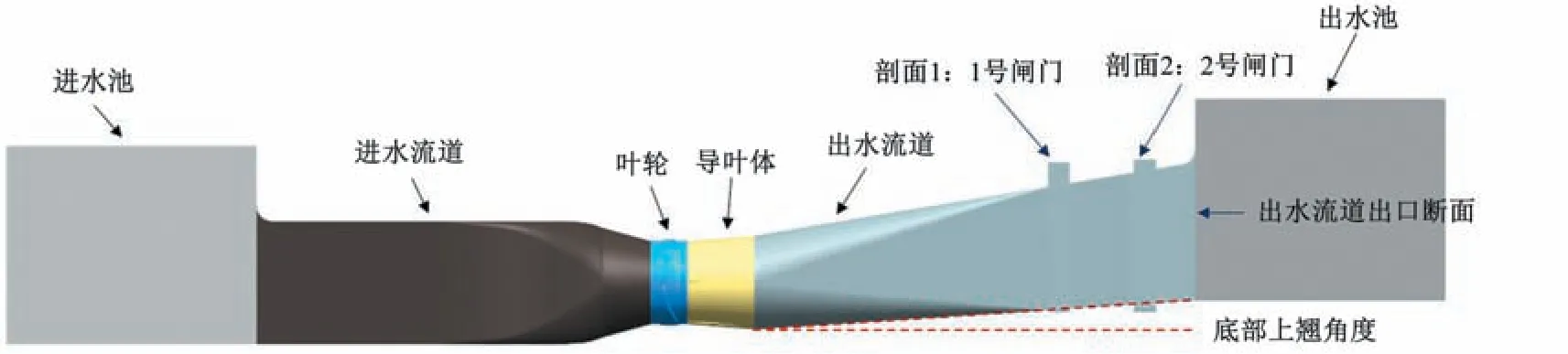
图8 底部上翘角度示意图Fig.8 Diagram of the upturned angle of the bottom

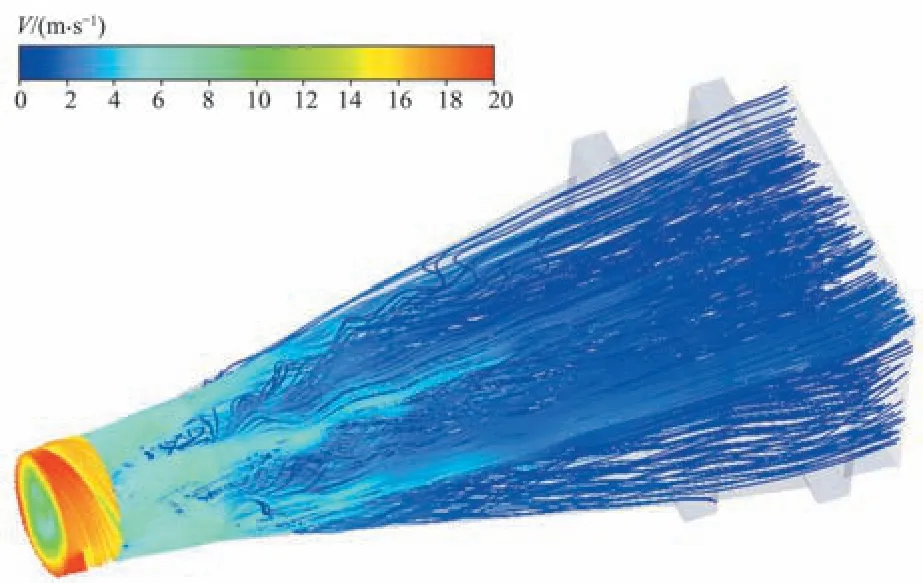
图9 θ=0°出水流道流场图Fig.9 Flow field diagram of outlet flow channel（θ=0°）

由于叶轮的高速旋转，导叶出口水流仍挟携部分剩余环量，导致水流以螺旋状流入出水流道，产生“贴壁效应”，使出水流道前部的断面流速呈现四周大，中间小的“靶状”分布，“贴壁效应”范围从出水流道进口至1号闸门前段；水流从进水流道进口断面至出口断面，流速逐渐降低。

根据数值计算结果，结合公式（4）、（5）、（6）求解得到，θ=0°出水流道的压力恢复系数为95.50%，水力损失为0.339 m，泵装置效率为71.65%。分析可知，出水流道动能回收率较高，水力损失较大，占设计扬程的17.1%，泵装置效率一般，有继续提升的空间。

3.3 底部上翘式出水流道水力性能分析

为了改善θ=0°出水流道的水流流态，探讨不同底部上翘角度对出水流道水力性能的影响，设置6 档底部上翘角度θ，分别为0.5°、1.0°、1.5°、2.0°、3.5°、5.5°。

根据数值计算结果，选取θ=1.5°和θ=5.5°作为典型方案，绘制流场图示于图10。由图10（a）可知，θ=1.5°出水流道内流流线较θ=0°无明显变化，流速分布相近，需展开进一步的定量分析；由图10（b）可知，θ=5.5°出水流道中部存在大尺度漩涡，水流流动条件恶劣，流态较差。

图10 底部上翘式出水流道流场图Fig.10 Flow field diagram of bottom upturned outlet channel

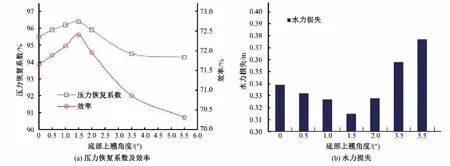
图11 上翘角度与水力性能关系Fig.11 Relationship between upturn angle and hydraulic performance

随着出水流道底部上翘角度的增大，泵装置效率与压力恢复系数均呈现先增大后减小的变化趋势，水力损失则与之相反，即当出水流道的动能回收率提升、水力损失降低时，有利于泵装置运行效率的提高。当底部上翘角度为1.5°时，出水流道水力损失和动能损失最低，泵装置效率最高，水力性能最为优异。

3.4 沿程涡通量分布

由于导叶体无法完全消除水流的旋转能量，因此出水流道进口水流仍挟携部分剩余旋转动能。文献［32］中提出导叶体出口水流的旋转强度可用通过导叶体出口断面的涡通量φ定量表示，计算公式为：

式中：Ω为速度矢量的旋度（Ω=rotv），s-1；v为速度矢量，m/s；S为导叶出口面积，m2。

将该公式应用于出水流道的涡通量计算，即出水流道断面涡通量的计算公式为：

式中：φout为出水流道的断面涡通量m2/s；Ωout为断面速度矢量的平均旋度，s-1；Sout为出水流道断面面积，m2。

勃列日涅夫时期，政治体制倒退，使得苏联在斯大林时期就存在的“特权阶层”进一步扩大与稳定，这一阶层的人思想更趋僵化，这也成为阻碍整个体制改革的一个重要因素。

通过式（8）计算出水流道断面的涡通量，以涡通量定义该断面水流的旋转强度。由图9、图11 可知“贴壁效应”的范围主要集中于出水流道进口至1 号闸门前段，因此选取该范围为出水流道涡通量的计算断面区域，设其总长度为1，沿轴向10 等分，即出水流道进口L=0，1号闸门前段L=1。

根据公式（8）计算得到出水流道前段沿程涡通量示于图12。由图12 知，出水流道水流从进口至1 号闸门前段经历了4个阶段：

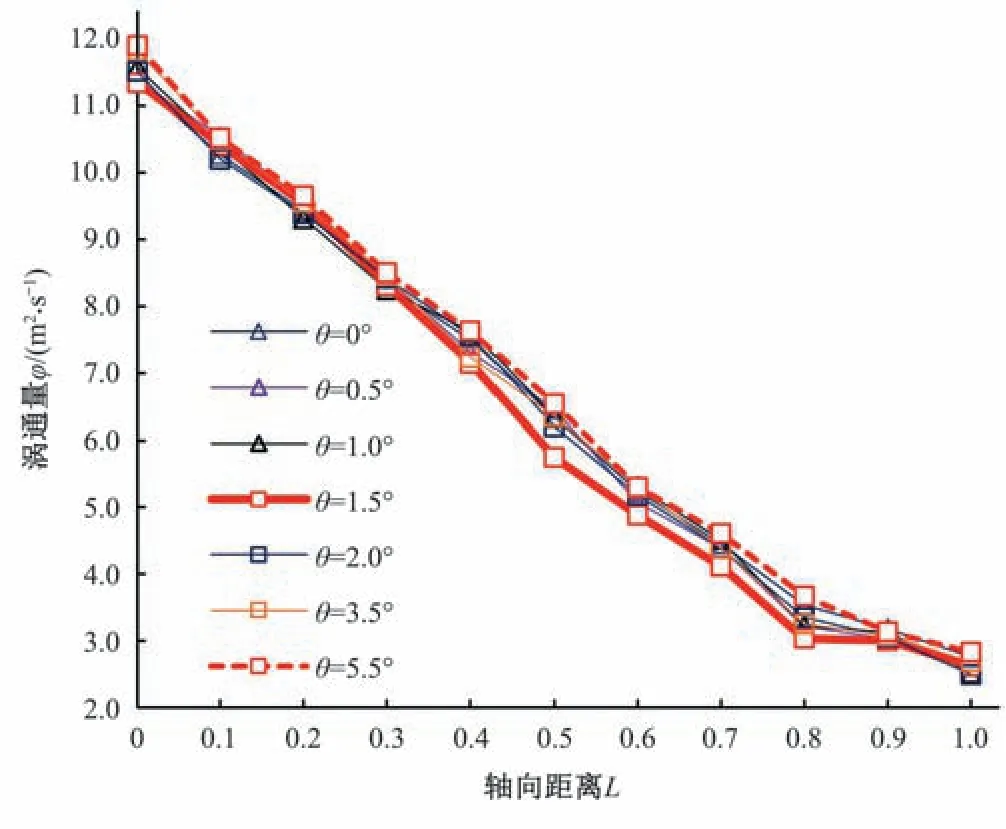
图12 上翘角度与涡通量关系Fig.12 Relationship between upturn angle and eddy flux

第一阶段为入流阶段（L=0），同样的入流条件下，底部上翘角度越大，水流的旋转强度亦越大。

第二阶段为紊流阶段（L=0.1～0.2），该阶段各角度涡通量基本保持一致，差异较小。分析其原因为该区域水流流态不佳，水流之间相互碰撞导致旋转能量的消散。

第三阶段为变流阶段（L=0.3～0.8），不同底部上翘角度的涡通量在该阶段出现较大差异。从L=0.3 至L=0.8 区域，水流的旋转强度仍为下降趋势，但旋转强度的降幅及下降速率存在差异，其中θ=1.5°旋转强度降幅最为明显，降幅达到5.28 m2/s，下降速率亦最快，出水流道对水流旋转的调整作用有所体现；θ=0°则基本保持了和前两个阶段相同的旋转强度降幅，流道对水流旋转的优化较为一般；θ=5.5°则出现了旋转强度降幅放缓的情况，这表明底部上翘角度过大时，流道对水流呈现负优化的趋势。

第四阶段为归流阶段（L=0.9～1.0），在L=0.9位置时，各角度涡通量归为一致（φout约为3.0 m2/s）。在该阶段，出水流道对水流旋转的调整作用逐步消失，出水流道内流流动方向从周向主导转为轴向主导，水流平顺，涡通量的变幅亦逐渐减小。

3.5 流速均匀度分布

在出水流道前段，水流的高强度旋转流动导致流速的“靶向分布”，因此其旋转强度是判断水流流动状态的主要参数。而在出水流道后段，水流旋转能量已经以水力损失的形式耗散，此时水流流向逐渐归于轴向，旋转强度较弱，故对出水流道后段流态的评判主要取决于典型断面流速分布的均匀程度。

选取1 号闸门断面（剖面1）、2 号闸门断面（剖面2）及出水流道出口断面（剖面3）计算各断面轴向流速均匀度，计算公式为：

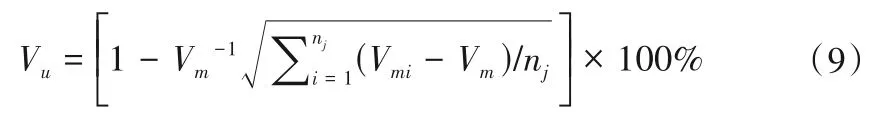
式中：Vu为断面轴向流速均匀度，%；Vm为断面平均轴向流速，m/s；Vmi为断面各单元的轴向流速，m/s；nj为断面上的计算单元数，个。

各方案断面轴向流速均匀度示于图13。由图13 可知，各方案从断面1 至断面3 的轴向流速均匀度均逐渐增大，增幅亦逐渐扩大。这表明不同的底部上翘角度对出水流道后段水流流速分布均具有正向调整作用，但作用强弱有所不同。

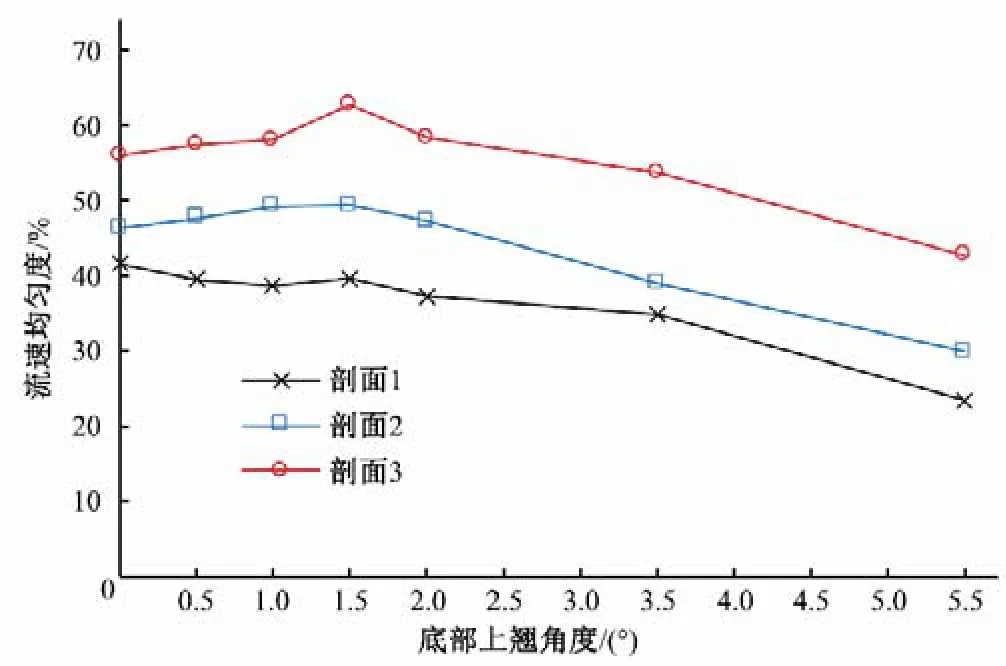
图13 上翘角度与流速均匀度关系Fig.13 Relationship between upturn angle and flow rate uniformity

随着底部上翘角度的增大，出水流道的流速均匀度呈先增大后减小的趋势，当底部上翘角度为1.5°时流速均匀度最高，水流可以以最佳的状态流出出水流道，出口断面流速均匀度为66.35%。当上翘角度过大时，出水流道对轴向流速的调整则较为乏力，流道内水流状态不佳，出水流道出口断面流速均匀度仅为42.75%。

4 结论

（1）以通吕运河泵站为例，采用ANSYS CFX 对不同底部上翘角度的直管式出水流道进行数值计算，结果表明存在底部上翘角度的最优阈值，为1.5°。采用阈值角度的底部上翘式出水流道，能够保持水流流动的稳定性，提高水力性能，增强其内流调整作用。

（2）随着出水流道底部上翘角度的增大，出水流道的水力性能呈先优后劣的变化趋势，当底部上翘角度为1.5°时，泵装置效率为72.41%，出水流道水力损失为0.315 m，压力恢复系数为96.4%，此时出水流道的水力性能达到最优。

（3）出水流道前段涡通量变化分为4 个阶段，分别为入流、紊流、变流及归流阶段，其中变流阶段是出水流道对旋转水流调整作用的显现，当底部上翘角度为1.5°时，变流阶段水流旋转强度降幅明显，为5.28 m2/s。

（4）各底部上翘角度出水流道的后段流速均匀度均呈上升态势，当底部上翘角度为1.5°时，出水流道后段流速均匀度的增幅最大，为21.41%，出水流道出口流速均匀度亦最大，为66.35%。

（5）直管式出水流道结构简单，设计形式具有高度的相似性，数值模拟结果表明直管式出水流道存在最佳的底部上翘角度，采用适宜的底部上翘角度能够提高直管式出水流道的水流性能，是合理可行的出水流道设计形式，值得在低扬程泵站中推广应用。