基于CMIP5 模式的不同集合方法对鄱阳湖流域降水及气温模拟能力的比较

吴 滨，刘卫林，郭慧芳，李 香，何 昊，刘丽娜

（1.南昌工程学院 江西省水文水资源与水环境重点实验室，江西 南昌 330099；2.浙江同济科技职业学院，浙江 杭州 311231）

0 引言

气候变化关乎人类命运，是国际热点问题。在全球变暖的背景下，众多学者开展了气候变化相关研究并进行了一系列的探讨。其中全球气候模式（Global Climate Models，GCM）作为气候模拟和未来气候变化情景预估的重要工具，被广泛用于探索和预测气候变化［1-3］。而耦合模式比较计划CMIP5（Coupled Model Intercomparison Project Phase 5，CMIP5）作为目前最为成熟的GCMs集合，在全球、地区气候变化及其影响研究方面受到了广泛的应用［4］。

CMIP5 模式的精度对研究结果的准确性至关重要［5］，不少学者评估了CMIP5 对中国地区降雨气温的模拟能力。陈晓晨等评估了CMIP5 对中国降水及气温的模拟能力，发现多模式集合预报精度优于单模式［6］。陶纯苇等人研究发现，在中国东北地区，模式对气温的模拟能力好于对降水的模拟能力［7］。张武龙等人通过2个技巧评分标准从34个模式中挑选出9种最优模式，发现最优模式集合对西南地区干湿季降水的模拟结果优于34 个模式集合平均和大多数单个模式［8］。根据已有的研究可以发现，通过择优、集合等方式可以提高CMIP5 模式对地区降水及气温的预报能力。在模式集合上，提出较早且使用较为广泛的是全模式等权集合［9，10］，之后择优等权集合［11］和非等权集合［12］等相关集合方法也被相继提出。择优等权集合是通过给定的单个指标或综合评分指标，根据模式的预报精度对多个模式进行排名，并选择排名靠前的几个模式进行集合的一种模式择优集合方法［13］。而非等权集合是通过统计学、机器学习等方法确定各个模式的权重并集合的方法，例如多元线性回归分析法［14］、贝叶斯模型平均（Bayesian Model Averaging，BMA）［15］和遗传算法［16］。有研究指出，BMA 集合预报优于简单集合平均［17］，但相关研究主要集中在气温方面［18，19］。

中国大部分地区四季分明，降水气温年内变化明显，同时由于复杂的大气环流以及海陆热力差异等复杂机制的影响下，年内旱涝并存、旱涝急转的情况时有发生［20，21］。而目前大多数学者主要注重模式及集合模型在年尺度上的拟合效果，对集合方法在年尺度、月尺度和空间上的比较关注较少。对于气候环境复杂的地区，多角度验证的多种集合的精度比较是有必要的。基于此，本文以鄱阳湖流域为例，基于CMIP5 的19 个气候模式数据，比较全模式等权集合、择优模式等权集合、全模式BMA 集合和择优模式BMA 集合在年尺度、月尺度和空间上的模拟精度，探讨其对流域降水与气温的模拟能力，为今后未来情景气候变化预估的集合方法选择提供参考。

1 数据与方法

1.1 数据资料

本文所用的19 个气候模式数据来源于http：//pcmdi-cmip.llnl.gov/cmip5/availability.html，模式基本信息见表1。

表1 CMIP5模式Tab.1 CMIP5 mode

研究选用实测资料为鄱阳湖流域26 个地面气象观测站的逐日平均气温和降水量数据，数据来源于中国气象局国家气象信息中心气象数据共享平台（https：//data.cma.cn/）。数据的年份为1961 年至2005 年。求出各个站点的月累计降水量和月平均气温，平均后即为流域月平均气温和月降水量。

考虑到CMIP5 各个模式分辨率不尽相同，为方便与观测资料对比分析，采用双线性插值法将CMIP5 各个模式的数据统一插值到观测站点上。

1.2 方 法

1.2.1 多模式集合方法

1.2.1.1 算术平均集成

算术平均集成是一种简单且常用的多模式集成方法，是将多个模式的模拟值进行算术平均，其计算公式为：

1.2.1.2 BMA方法

BMA 是一种结合多个统计模型进行联合推断和预测并可以产生高度集中的概率密度函数的统计后处理方法［22］。假设Y代表预测变量，f1，f2，f3，…，fn分别代表n个不同模型的预测结果，则BMA的概率预估可表示为多模式条件概率的加权形式：

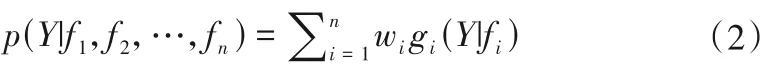
式中：wi为第i个模式权重，表示第i个模式在模型训练期对预报的相对贡献程度，非负且满足；表示预报变量Y在第i个模式预报fi下的条件概率。

BMA模型变量预报均值为［23］：

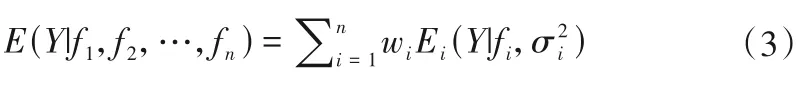
式中：σi为模型给定数据的模拟结果的方差，可以通过对数似然函数估计和，然后应用期望最大化算法（EM）对其进行求解。

1.2.2 模式评估方法

为客观评估CMIP5 各模式及各种集合方法对鄱阳湖流域气温和降水的模拟能力，本文引入了泰勒图分析方法。泰勒图是近年来被广泛应用于模式模拟能力评估的方法，它将模拟数据和实测数据之间的相关系数、标准差和中心化均方根误差综合展示在一张极坐标图上，能直观清晰地反映多个模式的模拟效果［24］。本文采用标准化泰勒图，即将泰勒图中的标准差、均方根误差用相对标准差和相对中心化均方根误差表示。其中相对标准差、相对中心化均方根误差及相关系数表达式分别如下：

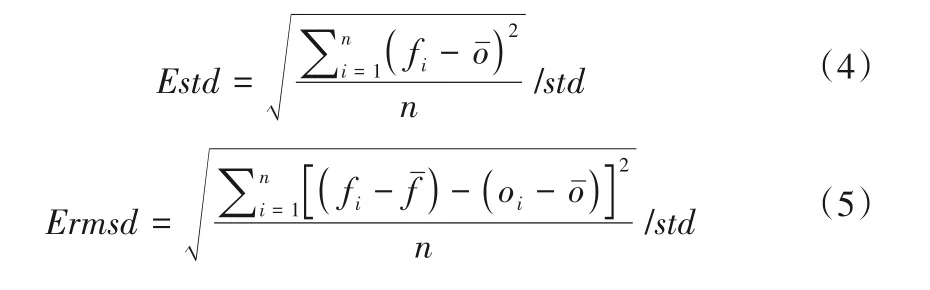
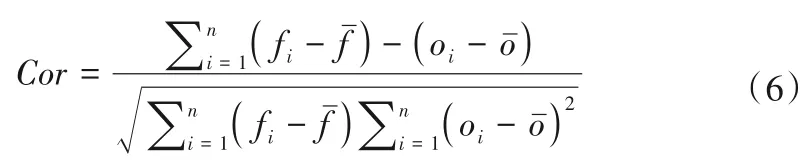
式中：std为实测系列的标准差；fi，oi分别为模式模拟值及实测值；n为CMIP5模式个数。

模式点离观测点越近，表明该模式的模拟能为越强。为方便，将相对标准差、相对中心化均方根误差简称为标准差和均方根误差。

同时，引入一个综合评价指标Ms来评价模式的综合模拟能力［25］。

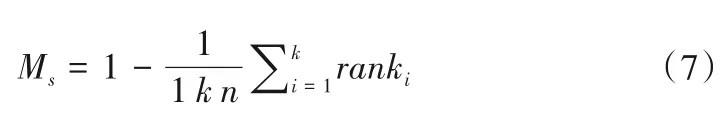
式中：n为选用的GCMs 个数（n=19）；k为评估指标个数，本文选择泰勒图中的标准差、中心化均方根误差和相关系数作为评估指标（k=3）；ranki为各模式在第i个评估指标下的排名。

根据选用的CMIP5 模式个数n的不同，本文用到的集合模型有全模式等权集合、基于Ms择优模式等权集合、全模式BMA集合（以下简称BMA 集合）、基于Ms 的择优模式BMA 集合（以下简称BMA-Ms集合）。

2 结果及分析

2.1 GCMs单模式比较与择优

2.1.1 气 温

图2 为CMIP5 单模式气温泰勒图。可以看出，不同模式对气温的模拟具有一定的差异，从均方根误差来看，最优的是MPI-ESM-LR 模式，其均方根误差为0.26，但其相关系数和标准差分别为0.97 和0.91，在19 个模式中排名第7 和第9。若从相关系数来看，最优的是CSIRO-MK360 模式，其相关系数为0.97，但其标准差为1.11，排第13。模式在不同的指标上有着不同的精度。根据Ms指标对CIMP5 单模式模拟能力排序（表2），综合最优模型是MIROC5，标准差、均方根误差和相关系数分别排第5、第2 和第10，而Ms 排名第2 的模型是MPI-ESM-LR，其标准差、均方根误差和相关系数排名分别为第9、第1和第7，Ms排名结果较为合理。根据Ms排序结果，气温择优建模的前6个最优模式为MIROC5、MRI-ESM-LR、Can-ESM2、CSIROMK360、IPRL-CM5A-MR、GFDL-CM3。

表2 各模式气温模拟精度排名Tab.2 Ranking of temperature simulation accuracy of each model

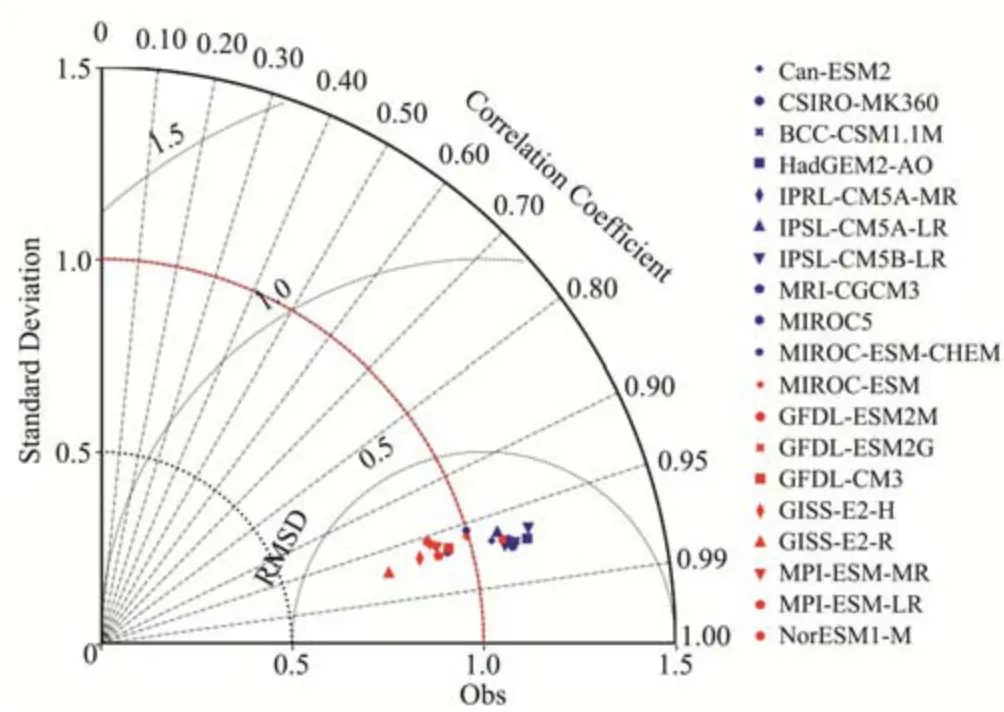
图2 气温泰勒图Fig.2 Temperature taylor chart

绘制实测值与Ms 排名前6 个最优模式的气温年变化过程（图3），可以看出鄱阳湖流域1961年至2005年多年平均气温为17.4 ℃，而Ms 排名第1 的模式MIROC5 模拟的多年平均值为17.7 ℃，整体偏高估了流域的气温；Ms 排名第2 的模式MPIESM-LR，其模拟的多年平均气温为17.2 ℃，整体低估了流域的实际气温。还可以看出，流域实测值变化范围为16.6～18.5 ℃，而部分模式的模拟值最低低于14 ℃，特别是排名第6 的模式GFDL-CM3其模拟的多年平均值仅为15.4，误差较为明显。

图3 流域实测气温与6个最优模式模拟值年变化过程Fig.3 The annual variation process of the measured temperature and the simulated values of the six optimal models in the basin

2.1.2 降 水

在降水方面，流域模式模拟值与实测值相关系数总体在0.4～0.6左右，小于气温（图4）。其中标准差、均方根误差和相关系数排名第1 的模式分别为MPI-ESM-LR、MIROC-ESMCHEM、NorESM1-M，模式在不同的指标下有不同的排名（表3）。在Ms排名中，NorESM1-M 排名第1，其标准差、均方根误差和相关系数分别为0.9、0.82 和0.64，排名第5、第2 和第1；而排名第2 的GISS-E2-H 其标准差、均方根误差和相关系数分别为0.87、0.83 和0.52，排名第8、第3 和第2，Ms 排名结果较为合理。根据Ms排名结果，降水择优集合的前6 个最优模式是NorESM1-M、GISS-E2-H、MPI-ESM-MR、GFDL-ESM2M、GFDL-ESM2G、MIROC-ESM-CHEM。

图4 降水泰勒图Fig.4 Precipitation Taylor Chart

表3 各模式降水模拟精度排名Tab.3 Precipitation simulation accuracy ranking of each model

绘制实测值与Ms 排名前6 个最优模式的降水年变化过程（图5），可以看出鄱阳湖流域1961年至2005年多年平均降水量为1 693.1 mm，其Ms排名第1 的模式NorESM1-M 的多年模拟值为1 370.6 mm，排名第2 的模式GISS-E2-H 的多年模拟值为1 586 mm，其他4 个模式的模拟值也低于实测值，6 个最优模式都低估了流域的实际降水量。同时流域在1963 年降水量为1 162.6 mm，是研究时段中的最小值，而集合中而排名第5 的集合GFDL-ESM2G，其最小值为1990年的614 mm，模拟误差显著。

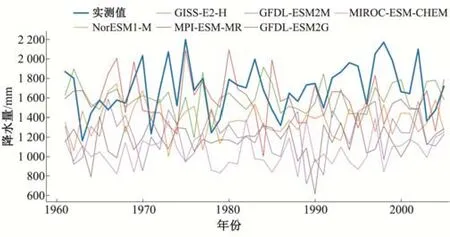
图5 流域实测降水与6个最优模式模拟值年变化过程Fig.5 The annual variation process of the measured precipitation in the basin and the simulated values of the six optimal models

总的来看，气温最优模式的3个泰勒图指标都优于降水，同时在泰勒图上，19个的模式的气温模拟值明显比降水更接近与实测点，这说明CMIP5 气候模式对气温的拟合结果好于降水。同时气温和降水基本都低估了流域的实测值，单一的模式与实测值有明显的误差。

这一区域人口规模多达2600万，太和医院的外来患者占了相当大的比例。门急诊大厅设有外埠患者接待中心，承接这部分患者。为了服务患者，太和医院医生和管理层还有颇多创意，其中就包括2013年成立的“星星急救科普小分队”。

2.2 集合在年尺度上的比较

以1961年至1995年为BMA 率定期，1996年至2005年为验证期，比较集合在年尺度上的模拟精度。

2.2.1 气 温

绘制流域气温实测值与各集合模型模拟值在1961 年至2005 年的年变化过程（图6）。可以看出在率定期，流域多年平均气温为17.3 ℃，而全模式等权集合和Ms 等权集合的多年平均气温分别为16.6 ℃和16.7 ℃，总体低估了流域的实际气温，而BMA集合和BMA-Ms集合的多年平均气温都为17.3 ℃，和实际值相等。在验证期，气温实际平均值为17.9 ℃，而全模式等权集合、择优等权集合、BMA 集合和BMA-Ms 集合的模拟值分别为17.1、17.3、17.7 与17.8 ℃。无论是在率定期和验证期，最接近实际值的集合为BMA-Ms 集合，其次是BMA 集合，而全模式等权集合和择优等权集合模拟值与气温实际值有着0.6 ℃的误差，模拟能力低于BMA集合和BMA-Ms集合。

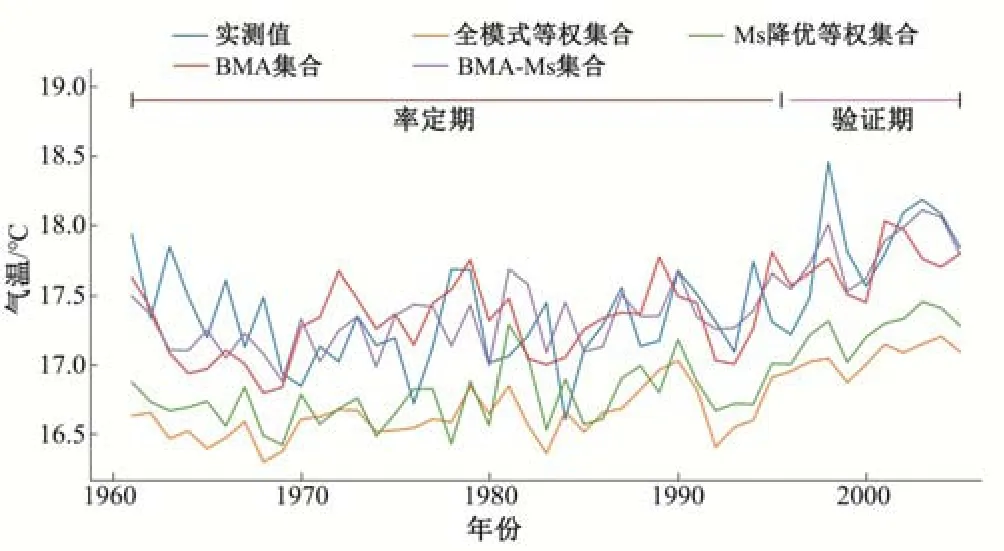
图6 流域气温实测值和集合模拟值年变化过程Fig.6 The annual variation process of the measured and ensemble simulated air temperature in the basin

2.2.2 降 水

绘制流域降水实测值和各集合模型模拟值在1961 年至2005 年的年变化过程（图7）。在率定期，流域实际多年平均降水量为1 671.2 mm，而全模式等权集合和Ms等权集合的模拟值为1 388.1 mm 和1 322.2 mm，与实际值差了300 mm 左右；BMA集合和BMA-Ms 集合的多年平均降水量与实际值相等。在验证期，流域实际多年平均降水量为1 769.6 mm，全模式等权集合、择优等权集合、BMA 集合和BMA-Ms 集合的模拟值分别为1 373、1 360.5、1 678.5和1 718.6 mm，可以看出BMA-Ms 集合的模拟值最接近实际值，其次是BMA 集合、全模式等权集合和择优等权集合。

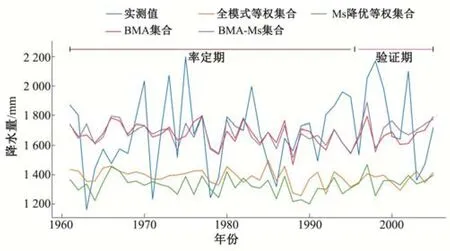
图7 流域降水实测值和集合模拟值年变化过程Fig.7 The annual variation process of the measured and ensemble simulated precipitation values in the basin

可以看出，无论是在率定期还是验证期，全模式等权集合和择优等权集合低估了流域的年降水量及年平均气温，而BMA集合和BMA-Ms 集合的模拟精度高于全模式等权集合和择优等权集合；其中BMA-Ms 集合的模拟能力好于BMA 集合，即在年尺度上，BMA-Ms集合对流域气候变化的描述更准确。

2.3 集合在月尺度上的比较

2.3.1 气 温

分别计算率定期（1961 年1 月至1995 年12 月）和验证期（1996 年1 月至2005 年12 月）集合气温模拟值与实际值的标准差、均方根误差、相关系数、相对误差和Nash 效率系数，根据这些指标对集合在月尺度上的精度进行说明，并以Ms 择优方法基于这5个精度指标对集合模拟效果进行排名（表4）。

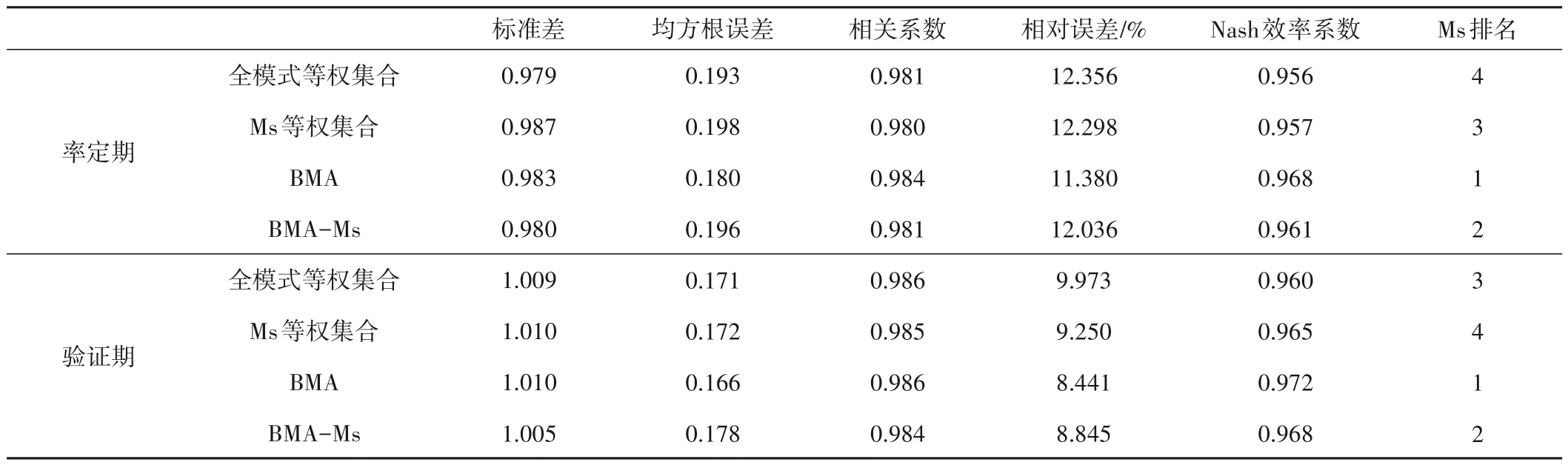
表4 集合模拟值气温结果比较Tab.4 Comparison of ensemble simulated air temperature results

在率定期，Ms 排名第1 的集合是BMA 集合，其标准差为0.983，仅次于Ms 等权集合，而其他的4 个精度指标都为4 种集合中最优值。BMA-Ms集合、Ms等权集合和全模式等权集合分别排名第2、第3 和第4。在验证期，Ms 排名第1 的集合仍是BMA 集合，除标准差外，其他精度指标都为4 个集合的最优值。排名第2、第3 和第4 的集合为BMA-Ms 集合、全模式等权集合和Ms 等权集合。可以看出，尽管在年尺度上BMA-Ms 集合气温模拟能力略好于BMA 集合，但是在月尺度的气温模拟上，BMA集合有着比BMA-Ms集合更好的表现。

为进一步观察集合在单个月上的气温模拟精度，绘制率定期12个月的流域实测值和4种集合模拟值箱型图（图8）。可以看出4 种集合气温模拟值从1 月至12 月表现出先增大、后减少的特征，与实际情况相符。实际值的上下限宽度和上下四分位数宽度基本大于集合模拟值，即集合模拟值的分布域宽度小于实际值，在模拟时可能会低估或高估月的实际值。例如在1 月份，全模式等权集合和Ms 等权集合的上限值仅等于实际值的中位数，而BMA集合和BMA-Ms集合的中位数基本等于实际值的中位数，但其上限小于实际值的上四分位数，4种集合都低估了1月的实际气温。在3月份，这4种集合的中位数基本等于实际值的上四分位数，集合模拟在一些年份会高估3 月份的实际气温。

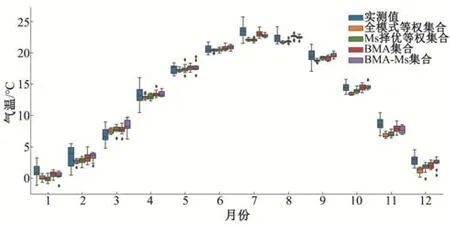
图8 验证期流域气温实测值与各集合模拟值箱型图Fig.8 Box plots of measured and simulated values of temperature in the basin during the validation period

2.3.2 降 水

以4种集合的降水模拟值与实际值的标准差、均方根误差、相关系数、相对误差和Nash 效率系数说明4 种集合方法在月尺度上的降水模拟能力（表5）。可以看出，在率定期，Ms排名第1的是BMA 集合，除相对误差外，各精度指标都为4 种集合方法中的最优值。排名第2、第3、第4的集合为BMA-Ms集合、Ms等权集合和全模式等权集合。在验证期，Ms 排名第1 的集合是全模式等权集合，其均方根误差、相关系数和相对误差为4种集合中的最优值，BMA集合排名第2。

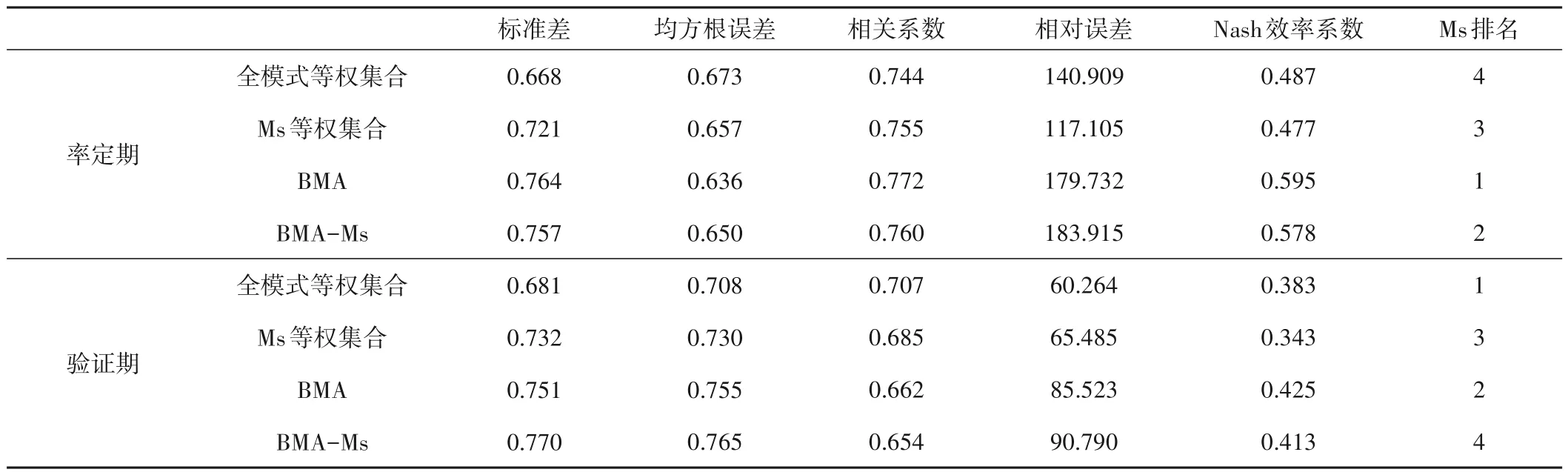
表5 集合模拟值降水结果比较Tab.5 Comparison of ensemble simulated precipitation results

为观察集合在单个月上的降水模拟精度，绘制率定期12个月的流域实测值和集合模拟值箱型图（图9）。在1月至5月，流域降水逐渐上升，4 种集合的模拟值也具有相同的变化。在6月，4种集合模拟的上四分位数都小于实际值的下四分位数，整体低估了流域6 月的实际降水量，其中BMA 集合和BMA-Ms 集合模拟值更接近实际值，模拟精度好于全模式等权集合和Ms等权集合。在6月至12月，流域降水基本呈现下降趋势，4种集合模拟值也具有相同的变化。

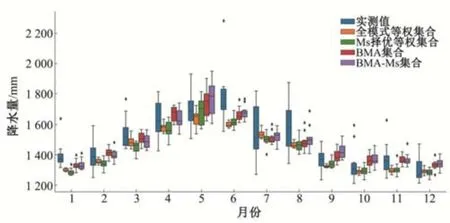
图9 流域降水实测值与各集合模拟值箱型图Fig.9 Box plots of measured values of precipitation in the basin and simulated values of each set

比较4种集合模拟值在月尺度上的精度后，可以看出，集合模拟值能够较好的表现出气温和降水在年内12个月上的变化，但可能会有高估或低估的情况。总的来看，BMA 集合在气温率定期、气温验证期、降水率定期Ms 排名都为第1，在降水验证期排名第2。模拟效果整体较好。

2.4 集合在空间上的比较

为验证4 种集合模型在流域空间模拟效果，通过反距离权重法绘制4种集合模型的气温与降水空间分布图（图10和11）。

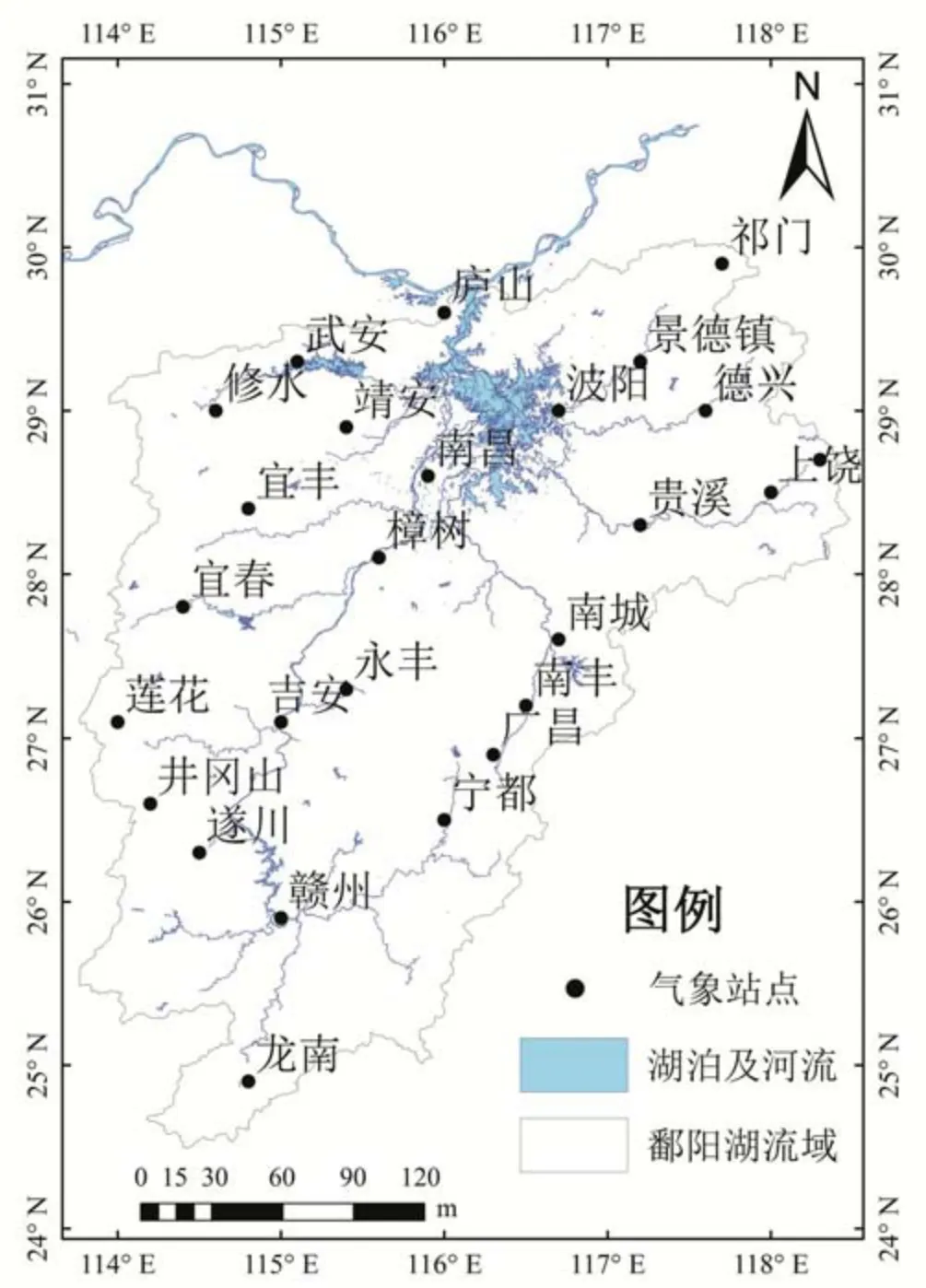
图1 研究区及相关站点Fig.1 Study area and related sites

2.4.1 气 温

从图10 可以看出，鄱阳湖流域气温具有南高北低，东高西低的特征，而全模式等权集合、Ms等权集合、BMA 集合和BMAMs 集合模拟值都能表现出气温南高北低这一特征，同时BMA集合和BMA-Ms 集合模拟值还较好的表现出流域气温东高西低的特征。在流域北部，大多数地区的多年平均气温为16.3～18.9 ℃，全模式等权集合和Ms 等权集合的气温为16.3～17.2 ℃；在流域中东部，地区平均气温为18～18.9 ℃，而全模式等权集合和Ms 等权集合的气温为17.2～18 ℃；总的来看，全模式等权集合和Ms等权集合低估了大部分地区的实际气温。而BMA集合和BMA-Ms集合模拟情 况符合流域的实际情况。

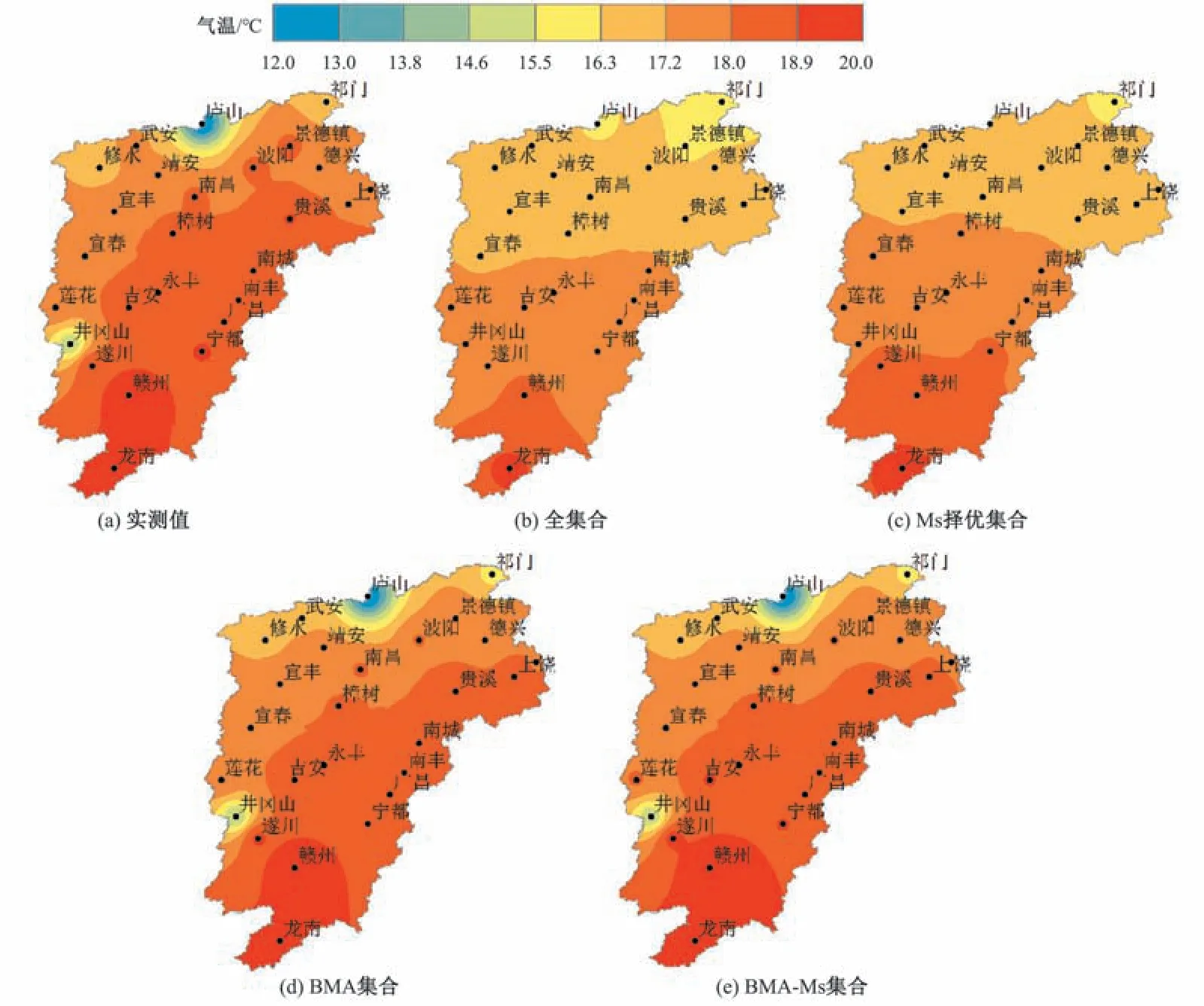
图10 流域气温分布图Fig.10 Distribution map of temperature in the basin

2.4.2 降 水

从图11 可以看出，鄱阳湖流域降水具有东高西低、北高南低的分布特征，且除龙南、赣州附近地区外，其他地区的多年平均降水量都达到了1 537 mm 以上，而全模式等权集合和Ms 等权集合模拟值在流域上都低于1 537 mm，低估程度较为严重。而BMA 集合和BMA-Ms 集合的模拟值在流域上表现出东高西低、北高南低的分布特征，模拟情况接近于实际值。

图11 流域降水量分布图Fig.11 Distribution map of precipitation in the basin

对比了全模式等权集合、Ms 等权集合、BMA 集合以及BMA-Ms集合的模拟能力可以发现，全模式等权集合和Ms等权集合整体低估了鄱阳湖流域的实际气温和降水年际波动、年内波动和流域多年分布，而 BMA 集合和BMA-Ms 集合的模拟结果更符合流域的实际情况，非等权集合方法的模拟精度高于等权集合方法。

许多研究都证实了GCMs数据对降水的模拟存在较大的不足［26］，特别是单个模式可能存在一定的误差，而在以往的研究中，大多数学者使用简单算术平均法进行多模式集合以提高模拟精度［27，28］。本文的研究结论指出，等权集合方法对气温和降水的模拟能力尽管好于单个气候模式，但可能会有较为明显低估情况，若不进行一定的校正可能会低估未来的气温和降水变化情况，因此在使用等权集合方法进行多模式集合时，可能需要根据实际情况进行模拟结果进行一定的校正，或考虑BMA等非等权集合方法。

3 结论

基于19种GCM降水与气温数据以及鄱阳湖流域26个气象站点1961～2005 年降水与气温实测数据，分析了全模式等权集合、Ms 等权集合、BMA 集合以及BMA-Ms 集合在年尺度、月尺度和空间上的模拟能力，得出的主要结论如下。

（1）19 种模式以及4 种集合方法对气温的模拟能力较好，对降水的模拟能力较差。

（2）在年尺度上，全模式等权集合和Ms 等权集合总的低估了流域的气温和降水；而全模式BMA集合和BMA-Ms集合能较好的表征流域多年气候平均态，其中BMA-Ms 集合的模拟能力最优。

（3）在月尺度上，全模式BMA集合的气温模拟效果最好，而在降水方面，不同集合方法在率定期和验证区有着不同的表现；在率定期全模式BMA 集合模拟效果最好，在验证期则是全模式等权集合模拟效果最好。从Ms 排名上看，全模式BMA 集合在气温率定期、气温验证期、降水率定期排名第1，在降水验证期排名第2，模拟能力总的较好。

（4）在空间上，流域气温呈现南高北低，东高西低的分布特征，全模式等权集合和Ms 等权集合仅能表现出南高北低的分布特征，且低估了流域的实测气温；而全模式BMA 集合和BMA-Ms 集合模拟值更接近流域的实际值且更符合流域的分布特征。在降水方面，流域降水呈现东高西低、北高南低的分布特征，全模式等权集合和Ms 等权集合模拟值明显低估了流域的实测值，模拟误差显著。而全模式BMA集合和BMA-Ms集合模拟值及分布接近流域实测值，空间模拟精度高于全模式等权集合和Ms等权集合。

（5）在年尺度、月尺度和空间分布上，4 种集合中对流域拟合最好的集合是全模式BMA集合和BMA-Ms集合；其中全模式BMA 集合在月尺度上好于BMA-Ms集合，而BMA-Ms集合在年尺度上好于全模式BMA集合。