百色水库入库径流中长期预测方法比较研究
2023-01-30唐振宇梁国杰张利平陈森林
唐振宇,梁国杰,张利平,陈森林,黄 馗
(1.武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2.广西电网有限责任公司,广西 南宁 530023)
0 引言
郁江是珠江流域西江水系最大的支流,属亚热带湿润季风山地气候,水能资源充沛,汛期受中层江淮切变线和华南静止锋的影响,其径流年际变化和年内变化显著,丰、枯水期径流量变化大。郁江流域水库、水电站众多,具有一定精度的郁江流域中长期径流预报对于其水库群优化调度以及水资源的优化配置具有重要的现实指导意义。
径流预报是水库优化调度的基础,准确的径流预报可以保证水电站正常运行,并安全、优质、经济地发供电[1,2]。径流预报的传统方法可分为数理统计法和物理成因分析法[3],其中数理统计法又可以根据预报所采用的基准对象不同划分为两类[4]:一类是基于径流时间序列本身的中长期径流预报方法,即找寻径流时间序列自身所存在的演变规律,常用的有自回归模型[5]等;另一类则是基于类似于气象因子等多变量的水文预报。近年来,许多人都做了相关工作研究。韩晓育等[6]将基于LASSO(Least Absolute Shrinkage and Selection Operator)回归的哈里斯鹰群算法(Harris Hawks Optimization,HHO)与支持向量回归(Support Vector Regression,SVR)耦合,对雅马渡水文站实测径流进行中长期径流预报并取得了优良的效果,但其仅仅考虑了年尺度的径流预报,并未考虑月、旬尺度;胡义明等[7]主要以平均合格率为评价指标,基于AdaBoost 模型对淮河干流王家坝站以及蚌埠站月径流进行中长期径流预报,取得了较好的预报效果;常新雨等[8]运用深度神经网络模型、Elman 神经网络模型和支持向量机预测模型对黄龙滩水库入库径流进行预测,在考虑了前期降雨量以及径流因素对径流时间序列的影响的前提下,取得了较好的预测效果;陶思铭等[9]使用长短期记忆网络模型(Long Short-Term Memory,LSTM)和BP(Back Propagation)神经网络模型对唐乃亥流域未来30天逐日流量进行预测,结果表明LSTM 具有较高的精度,但选取的对比模型较少,无法充分体现模型的优越性;Li Yujie等[10]以130个气候指标作为主要预报因子,采用随机森林模型(Random Forest,RF)和极端梯度提升树(EXtreme Gradient Boosting,XGBoost)两种集成学习算法对三峡水库入库流量进行预测时也仅考虑了大尺度的气候指标。
本文选用数理统计方法,充分考虑气象气候因子以及径流时间序列本身存在的数理统计规律,对比分析基于气象因子的逐步多元回归模型、神经网络模型(气象因子)和基于时间序列自身规律的最近邻抽样回归模型、小波分析法、混沌理论模型、神经网络—自回归模型共6 种模型方法在3 种不同时间尺度下郁江流域百色水库入库径流中长期径流预报的预测精度以及适用性。
1 材料与方法
1.1 研究区概况
百色水利枢纽工程位于右江上游河段[11],总库容56.6 亿m3。右江为郁江干流,其地处云贵高原东麓,地势西高东低,南北高中部低,为典型的河谷型丘陵地貌。百色水库处于亚热带季风气候区,光热充沛,雨热同季,夏长冬短。年平均气温在19.0~22.1 ℃之间,全年最高气温可达到36.0~42.5 ℃,最低气温低至-2.0 ℃,年平均降雨量为1 091.8 mm。汛期多集中在4-9月,且汛期降水量占全年降水量的80%[12]。百色水库为树枝状水库,流域如图1所示。其是以防洪为主,统筹兼顾发电、灌溉、航运、供水等功能的大(Ⅰ)型水库,多年平均流量为263 m3/s。百色水库坝址以上的集雨面积为19 600 km2,占整个右江流域面积的47.5%,流域内有西洋河、那马河、谷拉河、者仙河、乐里河五条较大支流汇入,集雨面积分别为5 070、1 318、2 400、790、1 416 km2。
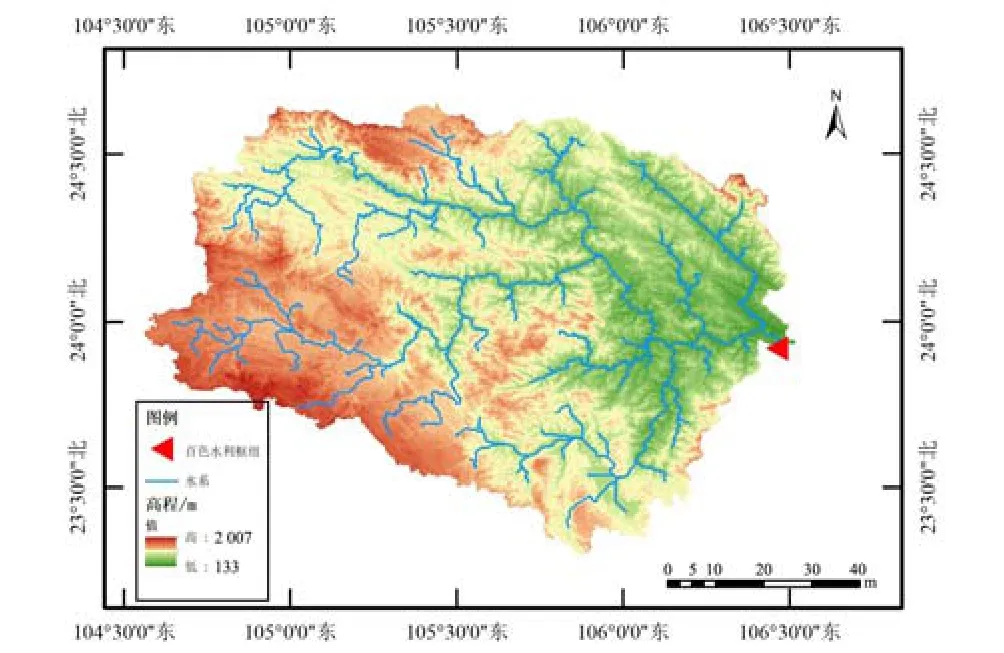
图1 百色水库水系图Fig.1 Water system map of Baise Reservoir
1.2 研究方法
1.2.1 基于时间序列的中长期预报方法
选用混沌理论、小波分析法、最近邻抽样回归模型以及神经网络—自回归模型四种基于时间序列的中长期预报模型方法对百色水库年、月、旬入库径流量进行预报。
混沌理论认为,客观事物的运动存在一种普遍的运动方式(混沌运动),即一种由确定性系统产生的、对初始条件具有敏感依赖性、永不重复的回复性周期运动。混沌理论模型对于实际问题往往得到一个间隔为∆t的单变量非线性时间序列,将混沌理论引入到非线性时间序列分析中,即是在时滞再造的思想上,进行一种有效的时空转换模式,在重构了相空间Rm[13]的基础上依据最短欧式距离在相空间Rm中以等间距采样的形式找寻时间序列x(t)的最邻近点,以此作为相位为τ的x(t+τ)的预测值。
小波分析法的基本思想则是用一簇小波函数来表示或逼近某一信号或函数[14]。本文将其与混沌理论模型相结合来进行中长期径流预报工作。小波分析法即是从时频分析的角度认为任意水文序列均由与其相匹配的制约因素和发展规律等多种频率成分构成。小波分析法可将水文时间序列分为多个频段的序列,进而分析不同频段水文时间序列的变化周期,从而判断出水文时间序列在变化过程中的主周期小波函数φ(t)。φ(t)为关于时间窗以及频率窗的双窗函数,其可通过调节两窗口的宽窄来应对尺度的变化。对于信号f(t)而言,通过连续小波变换可得到:
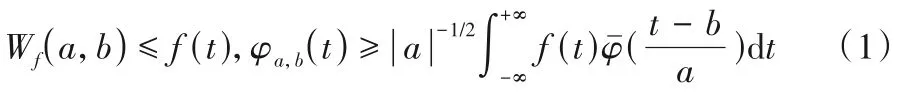
式中:a、b分别为表征频率以及时间的参数。
最近邻抽样回归模型是一类基于数据驱动、不需识别参数的非参数模型[15],其基本原理是:事物之间的发生以及发展存在着一定的联系,即在中长期水文预报中未来时间序列与历史时间序列的运动轨迹具有相似性。已知水文序列{Xt}n,Xt依赖于前P个相邻历史值序列Xt-1,Xt-2,…,Xt-P,将其序列定义为特征矢量Dt。最近邻抽样回归模型的思想就是对于已有的特征矢量中,总有K个特征矢量与当前特征矢量Di最近邻相似,两特征矢量通过欧式距离来判断其近邻情况。
神经网络—自回归模型是由神经网络模型在自回归模型理论基础上建立而成的。自回归模型是一种统计上处理时间序列的方法,根据同一变量之前各个不同时期的统计数值变化情况,预测该同一变量在未来一段时间内的数值变化[16]。自回归模型用于处理径流序列中的线性部分[17],神经网络模型则用于处理预测过程中的非线性问题。其通过单一时间序列的历史值序列来预测该序列的未来表现,即通过Xt-P,…,Xt来构建自回归方程预测Xt+1,…,Xt+N。神经网络—自回归模型通过人工神经网络模型与自回归模型的耦合来确定自回归方程系数,从而得以预测未来时间序列。
1.2.2 基于水文气象因子的中长期预报方法
本文选用了人工神经网络模型、逐步多元回归模型两种基于水文气象因子的预报模型方法对百色水库年、月、旬入库径流量进行预报。
人工神经网络模型是一种模仿人脑结构及其功能的非线性信息处理系统,具有自适应、自组织、自学习的能力,拥有较强容错性和非线性映射能力[18]。人工神经元是神经网络的基本处理单元,具有对每个输入信号进行处理,以确定其强度(权值)、所有输入信号的组合(加权和)、输出(转移特性)3 个基本功能[19,20]。人工神经网络模型是通过给定模型初始值,并依赖真实值对模型进行训练或修复,直至模拟值与真实值之间的误差在可接受范围内。
逐步多元回归模型通过建立因变量预测值与自变量因子值之间的回归方程,并对每一个引入方程的备选因子进行假设检验—F检验,并在逐步筛选因子的过程中生成过渡方程,直至方程既不能引入也不能剔除,即F检验通不过为止,则最终的方程是预报效果最佳的方程[21],也即应用实际变量建立的回归方程,如下所示:
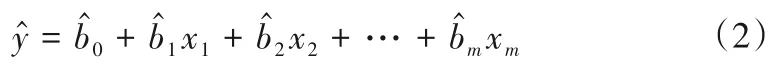
式中:m为因子数;xi为预报因子,i=1,2,3,…,m;为回归系数,i=0,1,2,3,…,m。
1.2.3 预报方案评估方法
文中的预报方案精度评定参照《水文情报预报规范(SL250-2000)》中的规定,除了采用平均相对误差、合格率、均方根误差3 项指标外,另外参考降水预报中的TS 评分建立径流预报TS评分指标,并在上述四个指标的基础上采用熵权法计算各个指标所对应的权值从而得出综合性指标来对比评价各模型的预测效果。
径流TS 评分指标是参考了降水预报中的TS 评分所建立的,即通过采用P-Ⅲ型频率曲线对历史径流序列进行适线,后反求频率为10%、25%、50%、75%、90%所对应的径流量,将径流量划分为6 个区间依次为特大流量、大流量、中偏大流量、中偏下流量、小流量与特小流量,若径流实测值与径流预测值处于同一区间,则认为该点处径流预报为正确预报。目前降水预报的TS评分一般在0.2~0.3左右,TS评分指标计算如式(3)所示。
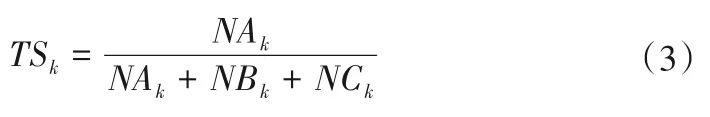
式中:TSk为第k等级的TS评分,TS的值介于0~1 之间;NAk为正确预报次数;NBk为空报次数;NCk为漏报次数;k为预报流量级别,此处分为6个等级。
综合性指标分析则是将平均相对误差、合格率、TS 评分指标以及均方根误差四者结合起来,利用熵权法计算出各个指标所对应的熵权值以得出4 个指标的客观权重,从而建立综合性指标来对比分析各模型的预报效果。熵权法赋权步骤如下:
(1)数据归一化处理。将本文中涉及的平均相对误差、平均合格率、TS 评分以及均方根误差进行归一化处理,即将各指标归一化到0~1的范围区间内。文中所涉及指标可分为正向指标(平均合格率、TS评分)以及负向指标(平均相对误差、均方根误差),对于正负向指标其计算方法不同,具体如式(4)所示:
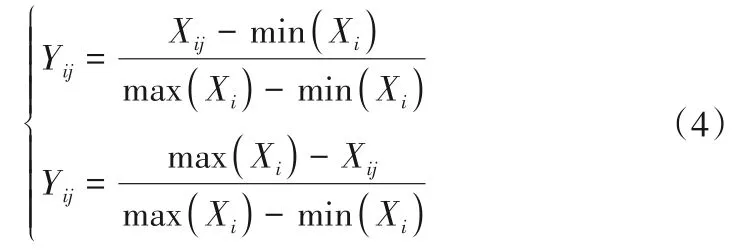
式中:i为指标个数,j为模型方法对应指标组数。由于本文涉及4个指标以及6个模型,则可有i=1,…,4、j=1,…,6。
(2)求各指标的信息熵。根据信息论中信息熵的定义,单个指标的信息熵如式(5)所示:
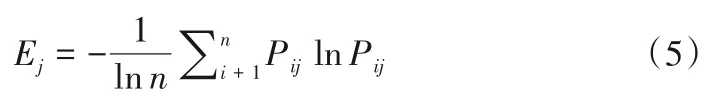
由于概率Pij是根据归一化处理后数据计算得到,其存在等于零的情况。此时lnPij的数值无意义,则规定其所定义的信息熵也为零。
(3)确定各指标权重以及得到综合性指标。由(2)得出各指标所对应的信息熵分别为E1,E2,…,Ek,则可得到各指标权重如下式所示:
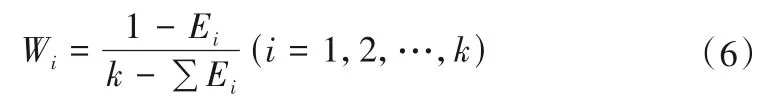
后将权重与归一化后的指标相乘并相加,得到一个0~1 的值用于评定各模型的预测效果。
2 应用结果分析
2.1 径流预测结果分析
选取百色水库1970-2019 年共50 a 的实测入库日径流数据、130项大气环流指数序列,通过计算得出相应年、月、旬径流数据,并借助相关系数法分析计算各因子与该站点相应径流序列的相关性,挑选出相关系数较大的前50 个因子作为待选因子,后采用逐步多元回归法分析这50 个因子,优选出4~8 个预报因子对于该站点的年、月、旬径流进行中长期预报工作。本文采用基于水文气象因子的逐步多元回归模型、神经网络模型和基于时间序列的混沌理论模型、最近邻抽样回归模型、小波分析法以及神经网络—自回归模型对百色水库入库径流进行年尺度、月尺度以及旬尺度的径流预报研究工作。由于两类模型原理、输入、输出以及预报尺度的不同,各模型将采用不同的模型参数率定期、检验期以及预见期进行径流预报工作,具体分布情况如表1所示。
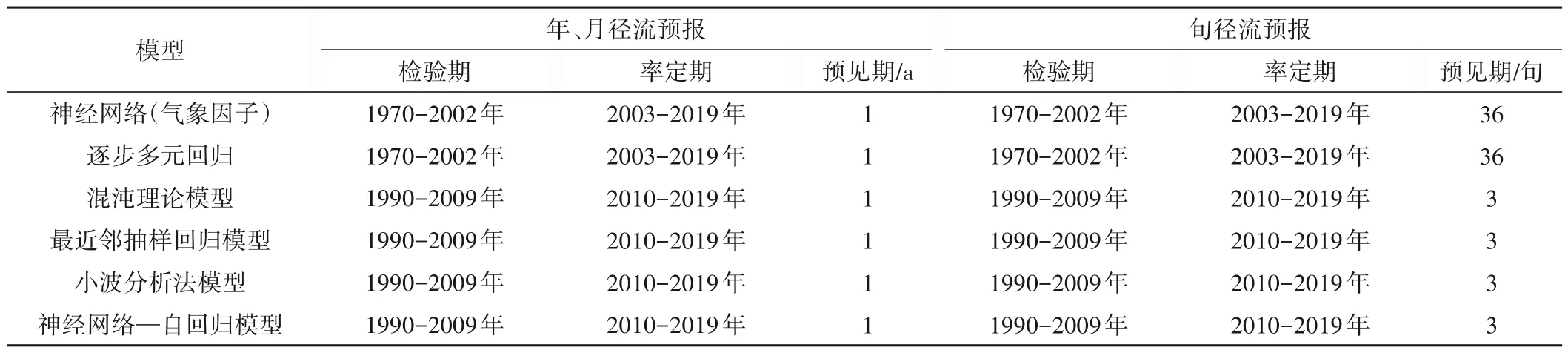
表1 各模型不同尺度预报率定期、检验期范围Tab.1 Calibration and validation period ranges at different scales for each model
2.1.1 年均径流预测结果分析
表2为百色水库入库年径流预报检验期各模型方法的平均相对误差、合格率、TS 评分以及均方根误差的精度评估指标结果。从表2 中可知:①基于气象因子的神经网络模型以及逐步多元回归模型检验期平均相对误差分别为57.19%、54.43%,远大于该两种模型在模型参数率定期时的平均相对误差,可能存在过拟合现象从而使得预测效果不理想。在基于气象因子的模型研究过程中,逐步多元回归模型的平均相对误差、总TS 评分以及均方根误差均要优于神经网络模型,而逐步多元回归模型检验期合格率却要劣于神经网络模型。②基于时间序列的中长期径流预报方法中,就平均相对误差而言,小波分析法的预测效果最好、最近邻抽样回归模型的效果最差;就合格率而言,小波分析法的预测效果最好,达到了70%,而神经网络—自回归模型处于一个较差的水平,仅为20%;就总TS评分而言,小波分析法模型表现最好为0.30,神经网络—自回归模型表现最差为0.10:就均方根误差而言,混沌理论模型、最近邻抽样回归模型以及小波分析法模型没有较大差别,而神经网络—自回归模型达到了较好水平,仅为111.43。
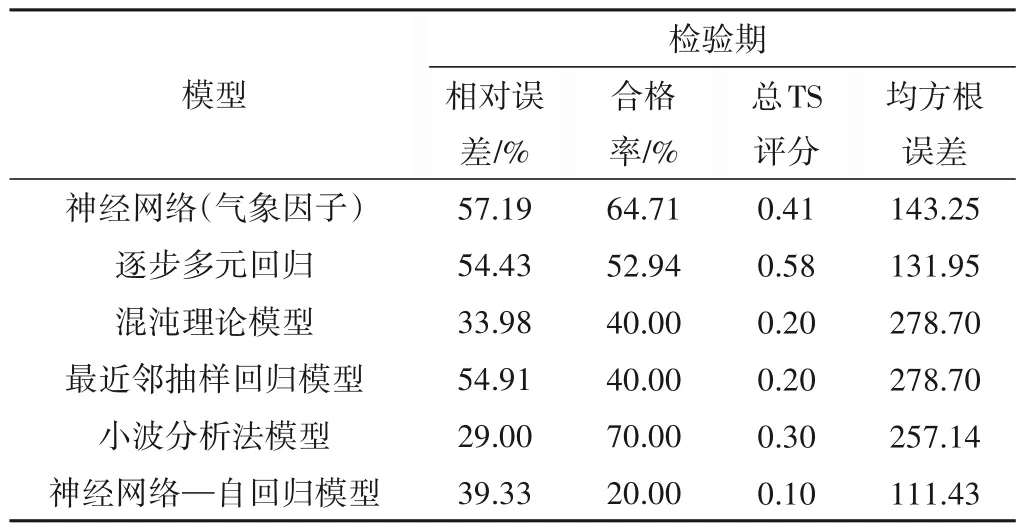
表2 各模型年入库流量预报误差结果评价Tab.2 Evaluation of annual inflow forecast error results for each model
由于基于气象因子的模型与基于时间序列的模型其预报结果的检验期以及率定期不同,故选取1990-2002 年以及2010-2019年径流序列和相应预测序列来展示各模型率定期以及检验期的预测结果,如图2 所示。在百色水库入库年尺度中长期径流预报工作过程中,就表征实测值与预测值之间差异性的平均相对误差这一指标而言,神经网络模型以及逐步多元回归模型这两种基于气象因子的中长期径流预报方法明显要劣于基于时间序列的中长期预报方法。由图2(a)率定期结果可知,其原因从模型特点来看,基于气象因子的神经网络模型以及逐步多元回归模型可能存在过拟合现象;从模型原理以及输入、输出的角度而言,气象因子可能与年径流之间变化趋势相关性不大。
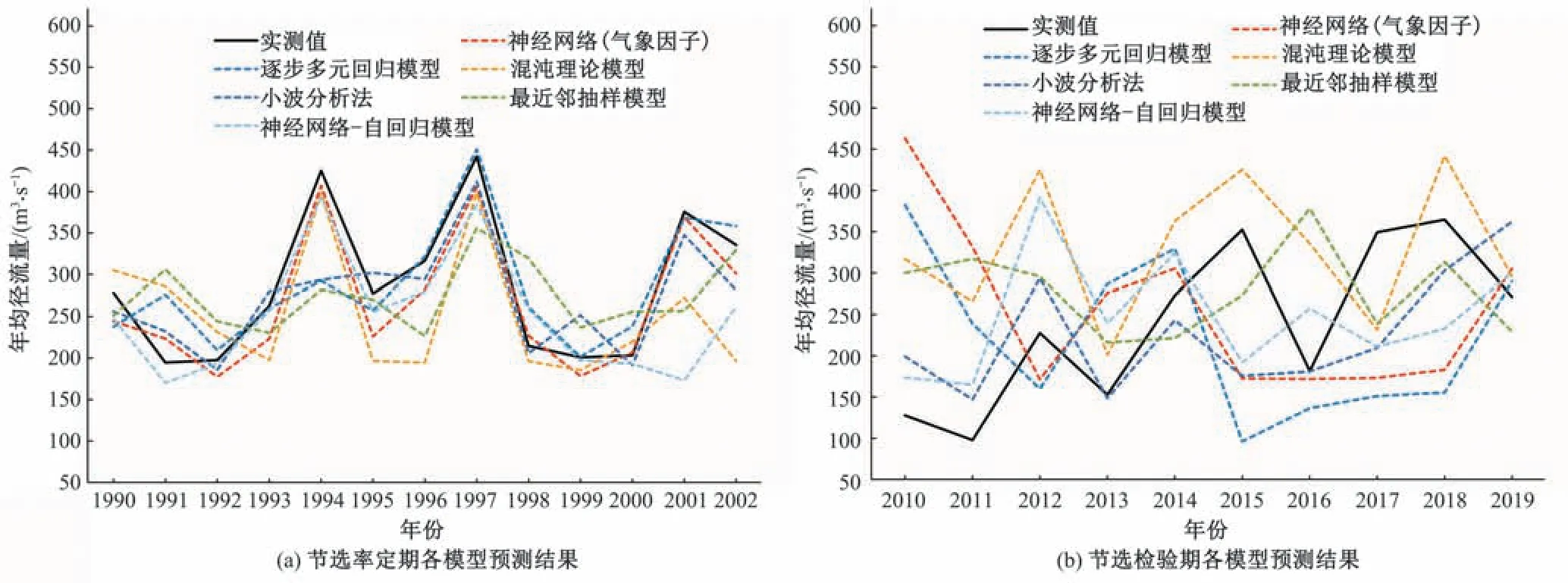
图2 各模型年入库径流量预测结果Fig.2 Predicted annual inflow runoff for each model
2.1.2 月均径流预测结果分析
由于基于气象因子的模型与基于时间序列的模型其预报结果的检验期以及率定期不同,故选取1990-2002 年以及2010-2019年月径流序列和相应预测序列来展示各模型率定期以及检验期的预测结果,如图4 所示。图3 为百色水库入库月径流预报检验期各方法的平均相对误差、合格率、TS 评分以及均方根误差的精度评估指标结果。由图3 可看出:①从各指标的均值曲线来看,各模型平均误差的平均值都偏大,达到了35%~60%的水平;合格率指标均值曲线均在0.6以上,处于一个很好的水平;TS 评分指标均值曲线维持在0.2~0.4 这一良好水平;均方根误差指标均值曲线在其进入汛期时有一个明显的爬升过程,进入非汛期又存在一个明显的下降过程。且各方法对于7 月、8 月、9 月汛期月径流预报的相对误差、合格率、TS 评分以及均方根误差都劣于非汛期时段。究其原因,由于研究区地处亚热带季风区,月降水的年际变化受季风气侯特点的影响呈现较大波动趋势、且汛期径流由于降水等诸多因素呈现出极强的不规律性,进而使得汛期径流预测精度较非汛期水平较差。②基于气象因子的神经网络模型在整体上相较于仅仅考量径流时间序列数值规律的预报模型的精度更高,其在如上的4 个指标中均有一个优良的表现。这说明在月尺度中长期径流预报过程中,气候所导致的径流序列波动能被表征气候变化的气象因子更好地表达。然而与其同样基于气象因子的逐步多元回归模型在7 月、8 月、9 月、10 月4 个月中,却存在平均相对误差相较于其平均值偏大的情况,且其均方根误差在5 月、6 月、7月也远远高于平均值,出现异常状况。
图4 各模型月入库径流量预测结果Fig.4 Monthly inflow prediction results of each model
2.1.3 旬均径流预测结果分析
由于基于气象因子的模型与基于时间序列的模型其预报结果的检验期以及率定期不同,故选取1990-1993 年以及2017-2019年旬径流序列和相应预测序列来展示各模型率定期以及检验期的预测结果,如图6 所示。图5 为百色水库入库旬径流预报检验期各方法的平均相对误差、合格率、TS 评分以及均方根误差的精度评估指标结果。
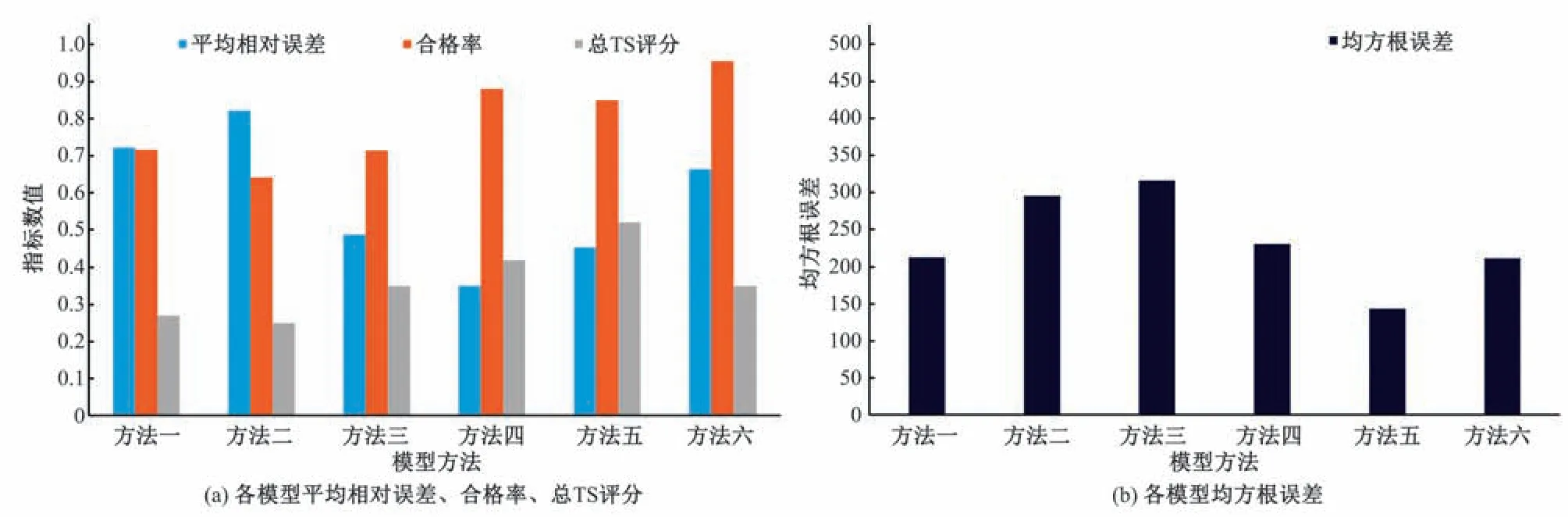
图5 旬入库径流量各模型预报检验期精度评定指标。Fig.5 Accuracy evaluation index of ten-day inflow forecast for each model’s validation period
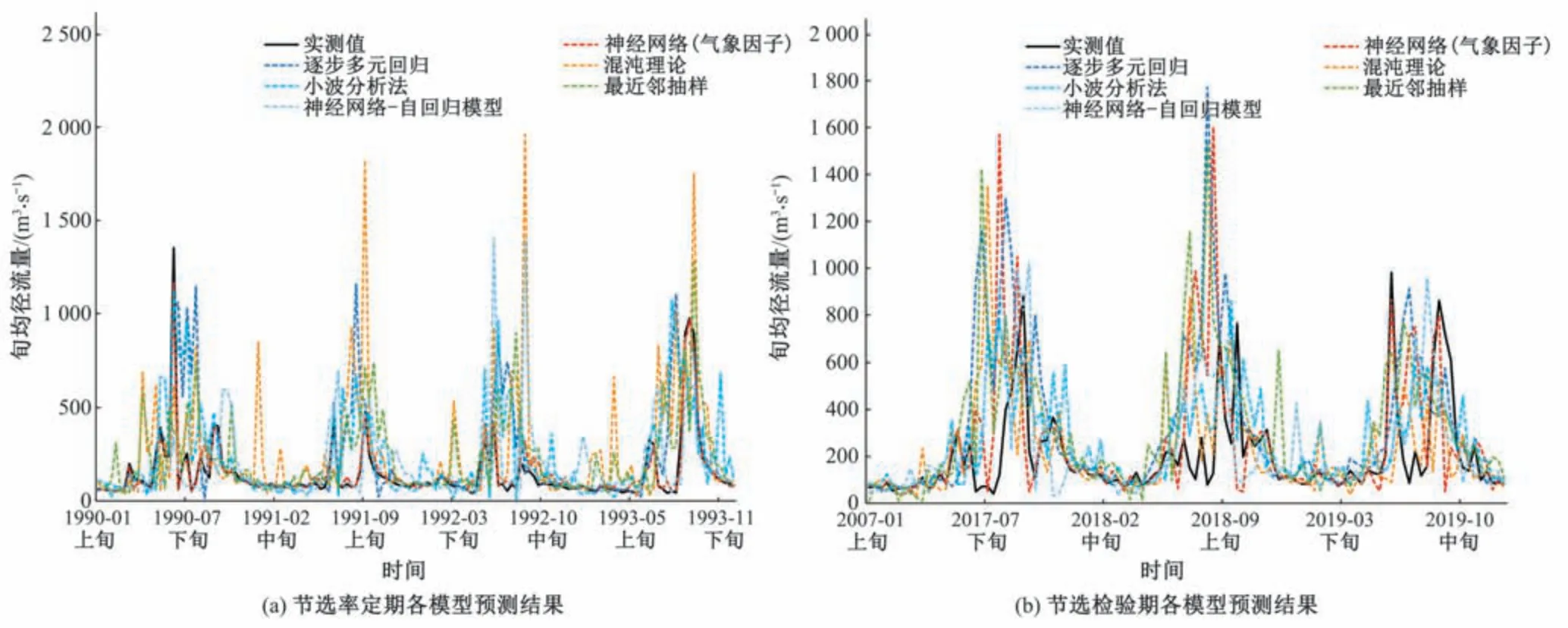
图6 近三年旬入库径流量各模型预测结果Fig.6 Ten-day inflow prediction results of each model in the past 3 years
从图6 中可看出:基于气象因子的神经网络模型及逐步多元回归模型中长期径流预报方法率定期率定效果很好,径流序列曲线几乎重合。而其检验期的平均相对误差则高达72.20%和82.20%,存在严重的过拟合现象。而基于时间序列的小波分析法、混沌模型、最近邻抽样回归模型率定期平均相对误差与检验期平均相对误差仅相隔4到5个百分点,预报效果良好。
从图5中可知:①在旬尺度入库径流预报过程中,基于气象因子的中长期径流预报模型的预报精度指标,例如检验期合格率、TS评分,均要劣于基于时间序列的中长期径流预报模型,气象因子在旬尺度上与其径流时间序列匹配程度较低。②整体上来看,各种方法的TS 评分均高于0.2(合理水平)。检验期TS评分总体都在0.25 以上,表明其预测结果的可行性。③6 种方法的合格率都处于一个较高水平(最低为逐步多元回归模型的64.1%,最高为神经网络—自回归模型的95.56%)。考虑到合格率的计算方法可知,其出现合格率高而误差相对偏大的情况是由于径流时间序列最大值与最小值相差甚远,而使得合格样本数偏高。④就6 种模型方法的均方根误差而言,基于气象因子的预测模型中,神经网络(气象因子)相较于逐步多元回归表现更好;基于时间序列的预测模型中,小波分析法模型表现最好、混沌理论模型预测效果最差。
2.2 综合评价结果分析
表3为百色水库年、月、旬入库流量预报各方法的综合性指标分析。综合评价即将平均相对误差、合格率、TS 评分以及均方根误差这四个精度指标根据信息熵的原理结合起来评价模型对于百色水库年、月、旬尺度中长期径流预报的优劣。由表3中的综合性指标分析可知:①年尺度的中长期径流预报过程中,基于气象因子的神经网络模型和逐步多元回归模型综合性指标分别为0.350 和0.403,逐步多元回归模型相较于神经网络模型在年尺度中长期径流预报中表现更好;基于时间序列的模型中,神经网络—自回归模型表现最好为0.891,最近邻抽样回归模型表现最差为0.268。②月尺度的中长期径流预报中,逐步多元回归模型相较于同类型的神经网络模型(气象因子)的预测结果更好。在基于时间序列的模型中,混沌理论模型预测效果最好,最近邻抽样回归模型则表现得最差。③旬尺度的中长期径流预报过程中,由于基于气象因子的模型与基于时间序列的模型预见期并不相同,故将两者分开比较。基于气象因子的模型中仅有两组指标参数,熵权法客观赋权不适用,故各指标人为主观赋权为0.25 得到综合性指标。基于时间序列的模型中仍采用熵权法客观赋权方法进行综合性指标分析。从结果中可看出,基于气象因子的模型中,采用神经网络模型(气象因子)进行36 旬预见期的旬尺度中长期径流预报工作;基于时间序列的模型中,采用小波分析法进行3 旬预见期的旬尺度中长期径流预报工作。
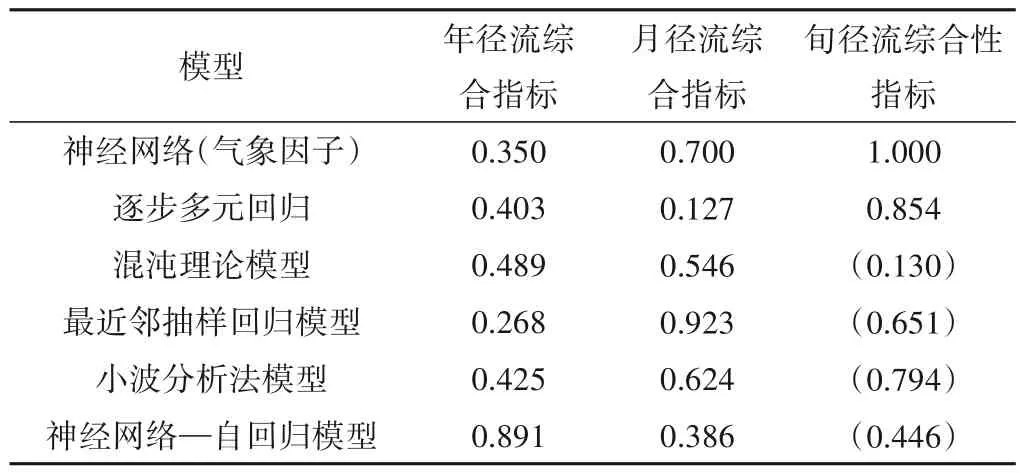
表3 年、月、旬入库流量各方法预报综合指标分析Tab.3 Each method’s comprehensive index for annual,monthly,and decadal inflow forecasts
3 结论
研究采用基于水文气象因子的逐步多元回归模型、神经网络模型(气象因子)以及基于时间序列的混沌理论模型、最近邻抽样回归模型、小波分析法以及神经网络—自回归模型进行郁江流域百色水库入库径流的年、月、旬尺度预报,并以相对误差、合格率、TS评分、均方根误差以及综合性指标分析来评定预报模型精度,其结论如下。
(1)依据综合性指标结果,在百色水库入库径流年尺度中长期径流预报中采用逐步多元回归模型、月尺度采用混沌理论模型、3旬预见期旬尺度采用神经网络模型(气象因子)、36旬预见期尺度采用小波分析法模型。
(2)由于百色水库入库径流序列极差相较于径流序列值严重偏大,且径流序列波动较大,从而出现各模型模拟的平均相对误差较大、而其合格率以及TS 评分等指标均为优良水平的情况。
(3)百色水库库区流域真实水文过程非常复杂,其径流过程受到诸多水文因素的影响。如想提高其中长期径流预报精度,还需进一步的研究。
