燃料电池AEC定容弹温度场计算分析

宋 俊,李明海,王贺武

(1.大连交通大学机车车辆工程学院，辽宁 大连 116028；2.清华大学车辆与运载学院，北京 100084)

1 引言

国家节能减排政策大力推广，全国各类用车，如工业用车、客车、私家车等都纷纷由“燃油”转向了“燃电”。电池关乎电动汽车动力性能的好坏，是电动汽车的心脏。锂电池能量密度高、无记忆效应等优点使其成为燃料电池的首选。其可靠性和安全性分析已成为整个行业的重要课题[1-2]。对燃料电池的热失控研究往往是在模拟加热设备上进行的。其中AEC(adiabatic explosion chamber)定容弹是一种展现燃料电池热失控以及热失控反应的综合实验设备[3-6]。AEC定容弹结构简单，加热均匀对加热触发电池热失控效果良好。可以深入研究电池热失控之后的一系列反应过程，对燃料电池安全性的探索提供关键数据[6-9]。定容弹外壳采用保温材料确保加热温度在设定的条件下，并设置相应的加热模式控制加热。根据研究的AEC定容弹，开展了加热过程的温度场研究,并构建了该加热过程的研究模式,通过采用惰性气体为主要研究材料,分析不同加热状态下的温度分布情况，并揭示了定容弹中氮气温度随时间的改变过程,为研究在高温下燃料电池的热失控作用奠定了理论基础[9-11]。

2 AEC定容弹装置

2.1 AEC定容弹结构以及加热棒的布置

AEC定容弹主架构如图1所示，该定容弹选用圆柱形结构作为弹体的主结构。定容弹内部净容积为82 L(根据UL9540A标准)，设计压力为0.7 MPa，弹体内的气体介质为氮气[12-15]。上下盖板以及筒壁上安装加热棒对定容弹加热，在定容弹筒壁外侧设置绝热层，减少热量的散失。由图1所示，由于加热棒与筒壁以及上下盖之间直接接触，所以传热效率高。另外由于加热棒是均匀分布在弹体壁面以及上下盖区域，可以实现定容弹内部的氮气均匀受热。

图1 定容弹内筒模型Fig.1 Model diagram of the inner cylinder of a constant volume projectile.

2.2 AEC定容弹加热模式

弹体内氮气的温度由定容弹上下盖以及筒壁上安装的热电偶进行测量。利用加热棒对定容弹进行加热，采用连续加热、均匀加热的加热模式，使得定容弹内气体介质均匀的达到实验预设温度，并且使弹体内的气体介质温差最小，利用均匀温升来控制加热过程。实验从室温开始记录温度，每加热1 min，温度升高1 ℃，每加热30 min保温5 min，最终加热到150 ℃。定容弹加热模式如图2所示。

图2 加热棒加热模式Fig.2 Heating pattern diagram of heating rod.

3 AEC定容弹计算模型

3.1 模型优化

AEC定容弹在加热过程中出现的热传导、热对流、热辐射、结构应力与变形等问题。因为边界条件有变化、计算公式的限制和动态的复杂性等问题，使得在实际的生产过程中计算有误差，所以在构建定容弹的有限元模型时需要进行相应的优化。在构建模型时会进行以下优化：

(1)经典的传热理论对AEC定容弹的加热过程同样适用；

(2)材料各向同性；

(3)相互结合的结构为一个等效整体、无间隙，热流与温度传递相对连续；

(4)定容弹体的加热棒视为发热均匀的体积热源。

3.2 设置边界条件

首先对定容弹进行抽真空以及充入惰性气体的操作，抽真空压力到达约0.004 MPa，然后进行充氮气处理使得压力达到0.1 MPa，重复两次操作，保证定容弹内的氧气含量低至不影响燃料电池热失控的发生。利用氮气作为气体介质进行研究，根据材料的不同，定容弹的结构主要分为两大部分：由铝制成的定容弹筒壁以及硅酸铝制成的定容弹上下盖。根据实验实际参数，设置初始温度为20 ℃，定容弹体里充氮气压力为0.1 MPa。加热过程：从室温加热，每分钟升高1 ℃，每升高30 ℃保温5 min，最高升到150 ℃。AEC定容弹材料的热物理性能如表1所示。

表1 各种材料的物理性能Table 1 Physical properties of various materials.

3.3 热力学分析

热力学分析主要是研究计算模型中的温度场分布及对热梯度、热流密度等物理量。温度场是指在某一时间的各点温度的总和。它是时间与空间关系的函数，其直角坐标系为：

t=f(x,y,z,τ)

(1)

式中：t为温度；x,y,z为直角坐标系的空间坐标；τ为时间。式(1)表示物体的温度在x,y,z三个方向和在时间上都发生变化的三维非稳态温度场。

3.3.1 控制方程

模拟计算过程中涉及的控制方程包括连续性方程(2)、动量方程(3)、能量方程(4)。

(2)

(3)

(4)

式中：ρ为密度；p为压力；ui为i方向上流体的速度分量；μ为流体的动力粘度；keff为有效导热率；Ji,j为组分i的扩散通量；Sh为能量源项。

3.3.2 瞬态热平衡矩阵

ANSYS Workbench能进行稳态热分析和瞬态热分析两种。稳态热分析一般方程为：

[K]{I}={Q}

(5)

式中：[K]为传导矩阵，包括热系数、对流系数以及辐射系数和形状系数；{I}为节点温度向量；{Q}为节点热流向量，包括热生成。

在周期性非稳态导热过程中，物体内各处的温度按一定的振幅随时间进行周期性波动；同时物体内的温度分布也成周期性波动，瞬态传热过程中系统的温度、热流率热边界条件以及系统内能随时间都有明显的变化。瞬态热分析满足q=dU/dz,即流入或流出的热传递速率q等于系统内能的变化。根据能量守恒原理，瞬态热力学分析一般方程为：

[C]{T}+[K]{T}={Q}

(6)

式中：[K]为传导矩阵，包括热系数、对流系数以及辐射系数和形状系数；[C]为比热矩阵，考虑内能的增加；{T}为节点温度对时间的导数；{Q}为节点热流向量，包括热生成[16]。

4 AEC定容弹温度场计算与分析

ANSYS作为一款有限元分析软件功能强大。其热处理的应用包括可对计算模型进行热传导、热对流、热辐射及接触热阻等问题进行分析计算求解[17]。

对温度场进行有限元分析方法可行、结果准确。因此采用有限元法对定容弹温度场的分布状况进行仿真研究。定容弹的加热过程为瞬态传热过程，其步骤如下：①前处理；②输入各个材料的热物理性能参数；③建立几何模型；④网格划分；⑤加载分析模块，设置加热时长和步长；⑥后处理，得到计算结果，输出计算数据，显示模拟结果。

4.1 计算模型的建立

首先利用SolidWorks软件对AEC定容弹进行三维建模，通过无缝接口将AEC定容弹优化后的模型导入ANSYS Workbench，对定容弹进行温度场的分析，并与定容弹实际温度场进行对比。分析在不同的时间节点处AEC定容弹的不同温度曲线。有限元计算只针对节点和网格，首先利用Mesh平台对网格进行划分，根据求解的需要在Mesh平台下进行四面体网格划分，设置剖分最小尺寸为0.012 mm，生成大约1 200 000四面体网格。局部结构网格如图3所示。

图3 定容弹局部网格Fig.3 Local grid of constant volume bullet.

4.2 AEC定容弹温度场分布

根据之前搭建的AEC定容弹模型，添加好材料参数以及相应的边界条件。定容弹绝初始温度为20 ℃，弹舱内填充的惰性气体介质为氮气，筒壁设置绝热层。设置求解步长为30 min，总时长为150 min。通过对边界条件以及计算参数的设定，计算定容弹在此运行状态下的瞬态温度场，待定容弹温升稳定后的温度场云图如图4所示。

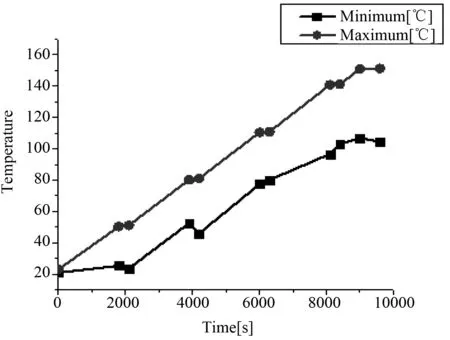
图4 加热150 min时定容弹温度分布Fig.4 Temperature distribution cloud of constant volume projectile at 150 min heating.

由图4和图5可见，AEC定容弹的最高温度为154.73 ℃，在定容弹的上下盖以及筒壁周围有加热棒的位置；最低温度为71.1 ℃，主要分布在上下盖没有加热棒的区域。当加热到150 ℃后，在对定容弹进行保温的过程中，定容弹体内各个点的温度差值之间变小。在垂直方向上，由于加热棒安装位置的原因，定容弹内的氮气温度不一致产生温度传递，使得氮气温度慢慢接近加热棒的温度。水平方向上温度基本成对称分布，由于盖板以及筒壁上有加热棒的原因，定容弹两端的温度相对较高，符合传热规律。

图5 加热过程中定容弹体温升曲线Fig.5 Temperature rise curve of constant volume projectile during heating.

由图6、图7可见，定容弹内氮气的最高温度为151.15 ℃，在靠近加热棒的位置，定容弹的最低温度为104.44 ℃，在定容弹的上盖附近没有加热棒的位置。由于定容弹的加热棒都给中间部分加热，所以中间位置的温度偏高。但是在连续的加热过程中，定容弹逐渐表现出温度的不均匀性，这同样表现出不同时刻的温度分布情况，定容弹内各点的温度梯度较为明显，筒壁附近的温度相对较高。因为金属筒壁的导热能力强，传热速度快，温升速度快，弹体其它区域温升相对较慢是因为与加热棒相距较远，且弹体内的氮气导热能力相对较差因此导致温度上升较慢。

图6 加热150 min定容弹内部温度场Fig.6 Temperature field cloud diagram of constant volume bomb after 150min heating.

图7 定容弹内部氮气温升曲线Fig.7 Temperature rise curve of nitrogen in a constant volume projectile.

4.3 AEC定容弹温度场分布

根据实际要求，主要对AEC定容弹内的氮气进行温度分析。在垂直和水平方向上，定容弹内的氮气对称分布，由于加热棒均匀分布在筒壁以及上下盖附近，因此氮气能够充分反映出温度的变化情况。按照连续加热模式，分别计算各点的温度，对定容弹内部氮气温度场分布情况进行研究。由表2可知，靠近筒壁的温度最高为154.73 ℃，靠近上下盖的区域的温度最低大约为71.1 ℃；定容弹内氮气温度最高151.15 ℃，最低为104.44 ℃。由于该结构特点，从图5中可以看出在温升阶段，靠近筒壁的区域温升更快，温度相对更高，弹舱内的氮气温度相对较低。从图5、图7中可以看出，随着加热时间的增加，当加热60 min后，弹舱内氮气最高温度为110.08 ℃，最低温度为75.775 ℃，当对定容弹保温5 min后，最高温度为110.22 ℃，最低温度为80.476 ℃。当继续给定容弹加热30 min，弹体内的最高温度为140.11 ℃，最低温度为95.384 ℃，对定容弹保温5 min，弹舱内的最高温度为140.28 ℃，最低温度为102.85 ℃。在保温过程中，定容弹内的氮气最高温度变化不明显，但是最低温度有很大的提升。同样，上下盖板由于材料以及设计的原因，散热面积大，温度传递较慢，热损失较大，温升慢。

表2 定容弹内氮气温升Table 2 Nitrogen temperature rise meter in the bomb.

4.4 燃料电池热失控实验分析

燃料电池的工作温度一般在30 ℃左右，温度太高会影响使用寿命。对于不同容量燃料电池的热失控行为进行相关实验，得到不同电池容量状态下电池热失控的温度如图8所示。

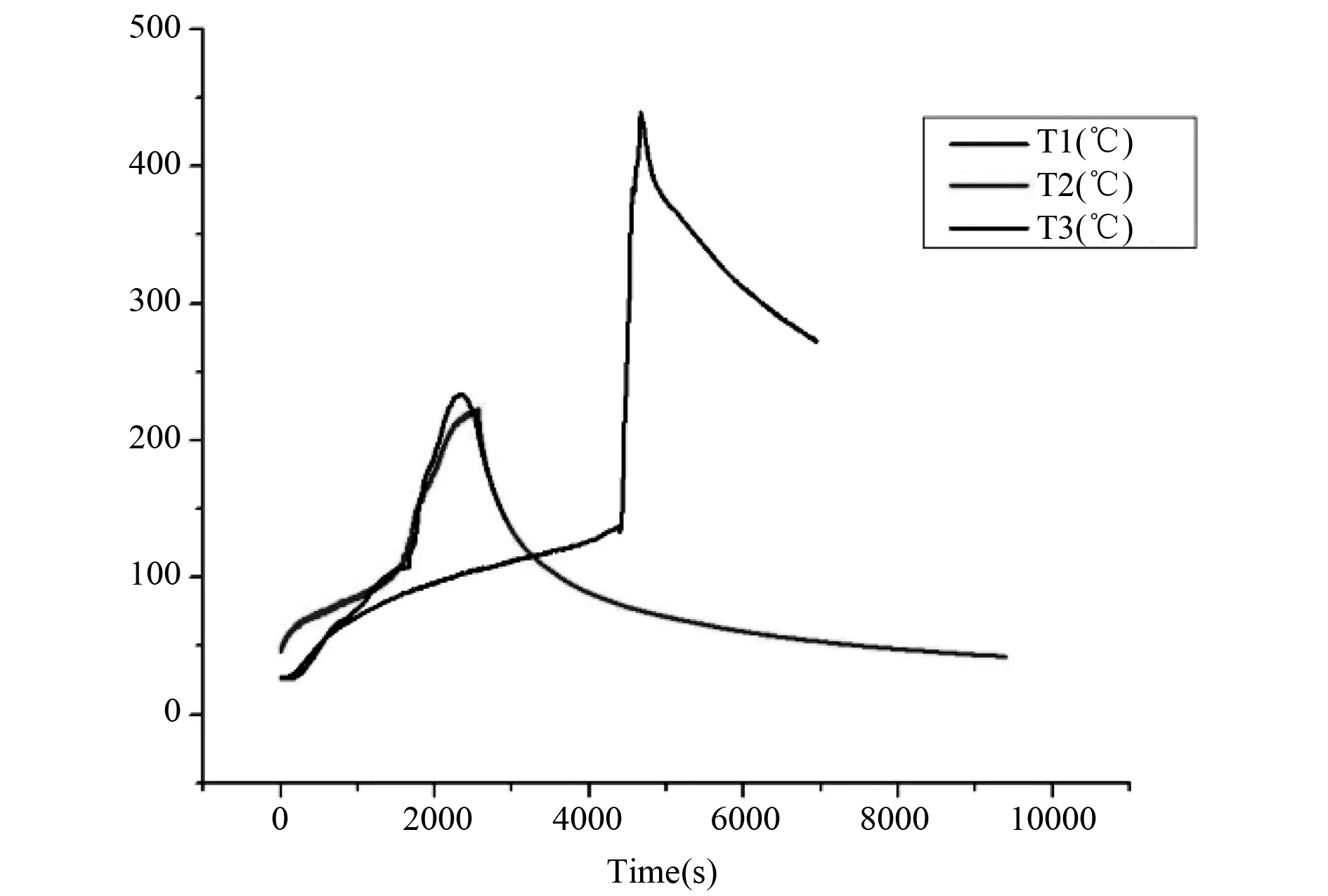
T1：176 Ah 100% SOC;T2：60 Ah 50% SOC;T3：60 Ah 100% SOC图8 不同容量电池热失控时温度Fig.8 Temperature diagram of batteries with different capacities when they are out of control.

通过图8可以看出环境温度升高导致电池发生热失控，不通电池容量的电池发生热失控的时间大不相同。相同容量电池不同SOC状态下电池热失控的温度相差不多，60 Ah电池热失控发生时温度在100 ℃左右。不同容量电池，容量越大发生热失控的时间越长、反应越剧烈。176 Ah电池发生热失控的温度大约在120 ℃。

5 结论

使用了有限元分析软件ANSYS对加热状态下的燃料电池中AEC定容弹温度进行热解析，从而获取了在各种加热模式下的各个时段内定容弹温度场的具体数值。并通过相应的燃料电池热失控实验数据如图8所示，以证明模拟过程的正确性。通过仿真结果，解析了AEC定容弹在加热状态下，弹内的流体介质温度场分布变化规律，结果如下。

(1)圆柱形AEC定容弹弹体在加热过程中，弹体中有加热棒的区域温度最高，在没有加热棒的上下盖的区域温度较低。

(2)加热状态下，定容弹内气体介质有一定的温度梯度，在垂直方向上，温度大致称对称分布，由于加热棒安装的位置的原因，定容弹内的气体介质温度有温度热量的传递现象，气体介质的温度慢慢接近定容弹筒壁以及上下盖的温度。

(3)在对定容弹保温的过程中，定容弹的最高温度变化不大，但是定容弹的最低温度温升相对较大，能有效降低温度梯度。

(4)定容弹测试温度与实际氮气温度并不一致，最高温度差距明显，平均温度基本一致。

(5)下一步将采用温升控制进一步降低温度梯度，保证定容弹内加热均匀。