涉及差分多项式的亚纯函数的唯一性

冯妍妍 ,林鸿金 ,许爱珠

(1.福建师范大学 数学与统计学院,福建 福州 350117；2.宁德师范学院 数理学院,福建 宁德 352100)

1 引言及主要结果

21 世纪初期,Halburd 等[1]、Chiang 等[2]揭开了对亚纯函数差分模拟理论研究的序幕.之后Halburd等[3]将相关理论中的增长级条件推广至超级小于1,唯一性理论得到极大发展.假定读者已经熟悉Ne⁃vanlinna理论的相关理论和符号[4-5],例如N(r,f),m(r,f),T(r,f),f(z+c)等.

为了介绍研究成果,现给出亚纯函数f(z)超级的定义,介绍f(z)的一类差分多项式M(f),并给出CM、IM分担a的定义.

定义1[4-5].

定义2令η为非零复常数,定义如下的差分多项式M(f):

其中：αi(i=0,1,2,…,p)均为常数,αp不为零且α0+α1+…+αp=0.

定义3[5]f和g均是非常数的亚纯函数,a∈.

1）若f-a和g-a有完全相同的零点,并且各个零点对应的重级相同,则称f和gCM 分担a,或称a是它们的CM公共值.

2）若f-a和g-a的零点相同(不计重数),则称f和gIM分担a,或称a是它们的IM公共值.

在复分析研究领域中,作为经典课题之一的亚纯函数唯一性理论是值分布理论的一个重要应用.1925年,Navanlinna证明了经典的四值定理,具体如下.

定理A[5]设f(z)和g(z)为两个非常数亚纯函数,且它们CM分担4个互相判别的复数a1,a2,a3,a4.如果f(z)≢g(z),则f(z)=T(g(z)),其中T为一个分式线性变换.

2018年,Qi等[6]考虑了f(z)与f(z+c)具有某些分担值的唯一性问题,证明了：

定理B[6]设f(z)是有穷级亚纯函数,c∈∈S(f)⋃{ ∞}是三个互异的以c为周期的周期函数.若f(z)和f(z+c)CM 分担a1,a2且IM 分担a3,则f(z+c)≡f(z),其中定义S(f)为f(z)的小函数的集合.

2020 年,Chen 等[7]和Qi等[8]从亚纯函数唯一性理论的角度出发,考虑了f(z)与之间的分担值问题,获得了如下结果.

定理C设f(z)是超越整函数,其超级ρ2(f)＜1.若0 是f(z)和的CM 公共值,并且非零有穷复数a是它们的IM公共值,则f(z) ≡Δncf(z).

2022 年,林鸿金等[9]基于上述已有的结果,增加考虑了f(z)是有理函数的情况,将f(z)从超越整函数推广至非常数亚纯函数,得到如下定理.

定理D设f(z)是非常数亚纯函数,其超级ρ2(f)＜1,c(≠0) ∈.如果0,∞是和f(z)的CM公共值,非零有穷复数a是它们的IM公共值,且Θ(0,f(z)) ＞0,则f(z) ≡Δncf(z).

定理1设f(z)是非常数亚纯函数,其超级小于1,c(≠0) ∈且a为可判别有穷复常数,M(f)如定义2中所定义.若M(f)和f(z)CM分担0,∞,IM分担a,同时满足

Θ(0,f(z))＞0,

则f(z)≡M(f).

注下面给出例子来说明存在满足定理1的亚纯函数.

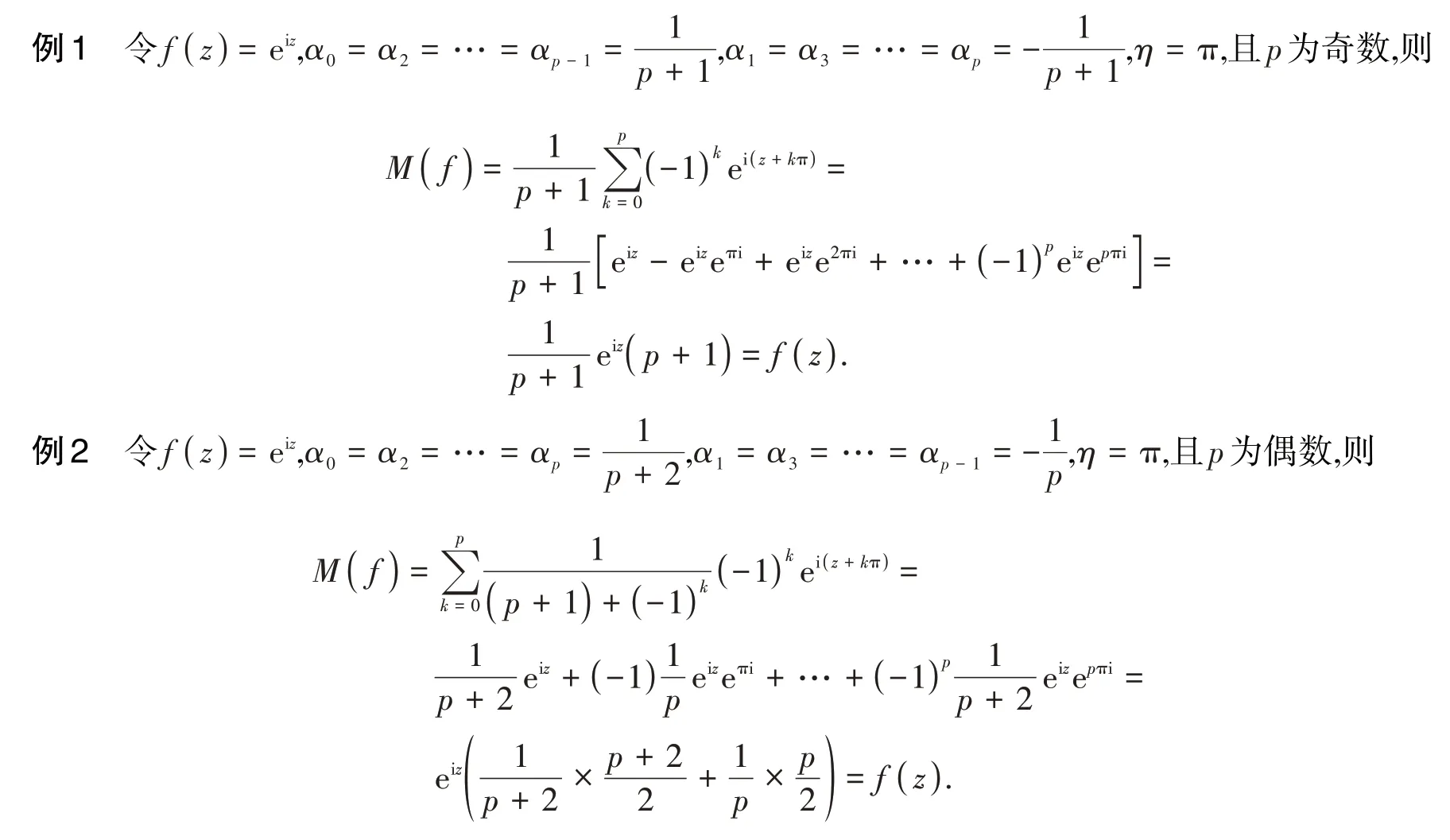
2 引理

引理1[3]设f(z)为非常数亚纯函数,其超级严格小于1,则

引理2设f(z)为开平面上的非常数亚纯函数,M(f)如定义2中所定义,a为任意有穷复数,则

3 定理1的证明