一种基于光流跟踪的航天器多未知地标导航方法
2023-01-29郁丰,陈阳,踪华
郁 丰,陈 阳,踪 华
(1.南京航空航天大学 航天学院,南京 211106;2.空间光电探测与感知工业和信息化部重点实验室;南京 211106;3.宇航智能控制技术国家级重点实验室,北京 100854)
航天器自主导航技术有效降低了航天器对地面测控的依赖程度[1],同时缓解了国土面积有限对地面站布局的限制。使用光学图像进行航天器自主导航,具有抗干扰能力强、导航信息丰富的特点,且因航天器大都携带有光学相机,意味着使用光学图像进行航天器自主导航可有效节省载荷空间。根据对图像信息处理方式的不同,目前航天器光学导航主要分为基于已知地标和未知地标的导航方法。
依靠已知地标的自主导航方法,通过图像中的地标与本地地标库匹配识别来解算航天器的位置和速度。李木子[2]通过中心投影几何原理建立观测模型,并借助滤波算法构建完整的已知地标自主定轨算法。由于已知地标导航的高可观测性[3],该方法具有精度较高的特点,但同时也对成像环境与地标识别精度提出了较高的需求,且需要建立具有庞大数据量的高精度地标库,造成较大的存储压力。
未知地标,即地理位置对导航系统来说先验未知的陆地特征。使用未知地标进行航天器导航,任何易于光学跟踪的地标均可提供导航信息,无需关注地标的匹配算法,且地标目录和计算机存储需求可以显著降低。该方法使用地标传感器,将对同一未知地标的两次光学观测的视线矢量(Line of Sight,LOS)组合为观测值,通过递推导航理论求解航天器的六个状态量。Toda 将观测的地标位置偏差引入状态量[4],建立了地标位置偏差量在地球不自转假设下的转移矩阵,该滤波器可设计用于估计六个星历状态变量,同时补偿但不估计地标的三个位置偏差。仿真结果显示,轨道高度为257 km 的航天器,在运行8 轨并保证稳定跟踪轨道面内共6 个地标的理想条件下,定位精度可达到1 km 以内,由于地标位置并未直接估计,且该方法同时只能跟踪一个地标,导致其虽然可观,但收敛速度较慢。值得注意的是,地标固连在地球上,其位置受到中心天体椭球方程的约束[5],而这些约束在上述文献中被忽略了,同时地标跟踪传感器的特性决定了航天器同时只能跟踪单个或少数地标,导航数据受限。
随着视觉导航的兴起,2019 年,John[6]使用光学相机取代地标传感器,传统的视线矢量LOS 可使用地标的图像坐标代替。同时,对地标的跟踪不再局限于单个地标。该方法同时对多个地标进行位置估计,并拟合为椭球面对地标位置进行约束,通过最小二乘法对航天器状态及地标位置进行估计,实现使用非迭代方法的初始定轨。依靠12 min 数据弧内的三个状态估计达到了较可观的初始定轨精度,位置误差及速度误差分别为2.15-7.16 km、5.92-7.81 m/s。为了拟合较为平滑的椭球面以减小定轨误差,该方法对地标组合的选取提出了较高的需求,且并未考虑地球自转,仅适用于初始定轨方案,从图像序列中获取的定位信息并没有被完全利用。最后,由于数据集的获取困难,已有的研究均未将实时图像处理及地标跟踪作为研究的重点,但在实际应用中,不论是使用地标跟踪传感器,还是使用光学跟踪,跟踪误差及跟踪丢失的情况是不可避免的。
针对上述问题,本文使用模拟的遥感图像序列作为标称数据,设计了一种同时跟踪多个地标的未知地标导航系统。无需伺服机构,无需航天器调姿,通过相机内参获取每个采样地标对应的视线矢量LOS,实现多地标同时跟踪,地标更新快,导航信息丰富且更新周期短。利用几何约束对其在地球的位置进行初始化,直接将地标的位置引入状态量,使用状态方程将地标位置约束在旋转椭球体上,相对于John 使用最小二乘法拟合椭球面,降低了对地标分布的需求,且引入了地球自转。对遥感图像序列,采用Lucas-Kanada 稀疏光流法(LK 光流法),对地标点进行光学跟踪观测。将视线矢量LOS 作为观测量,通过扩展卡尔曼滤波器(Extended Kalman Filter,EKF)对航天器位置、速度及地标位置进行估计。本方法不仅使用了具体的遥感图像序列,对地标光学跟踪误差进行了量化,并且充分利用图像序列中每一帧的导航信息,获得了更佳的导航精度。
1 未知地标导航方案
航天器在轨运行期间获取遥感图像序列,从图像中提取一定数量的地标,这些地标对于导航系统来说是先验未知的陆地特征,在方便的观察范围内,任何清晰可辨且易于跟踪的地球特征都可以作为地标。通过不断跟踪地标获取视线矢量l,对地标在地球上的位置p与航天器的位置、速度r、v进行持续估计,如图1 所示。

图1 未知地标导航Fig.1 Navigate using unknown landmarks
1.1 导航系统流程
导航系统流程被分为量测信息获取及导航解算两个部分,如图2 所示。其具体导航步骤如下:

图2 自主导航系统流程Fig.2 Autonomous navigation system process
步骤1航天器运行过程中,实时获取对地的遥感图像,提取图像中的特征点作为待跟踪地标,结合相机内参,通过地标的像素坐标计算视线矢量l。
步骤2结合地球的三轴椭球模型及自转模型,获取待跟踪地标的位置初值p。
步骤3获取随后的图像帧,使用光流法对采样地标进行光学跟踪,提取新的视线矢量l。
步骤4将步骤3 中获取的视线矢量l作为观测信息,结合航天器轨道动力学模型以及地标推算模型,用于最优滤波估计。
在航天器运行过程中,由于图像的不断更迭,地标点的丢失是不可避免的。故在步骤3 中,当此帧现存的地标数目低于一定阈值时,将以步骤1、步骤2的方式进行地标点的补充。
2 未知地标导航算法
2.1 状态模型

在航天器的轨道动力学模型中,坐标系选取历元J2000.0 地心赤道惯性坐标系,摄动量考虑地球非球形引力J2项。
轨道动力学部分的状态模型可表示为:

其中,pi、pe分别为地标在地心惯性系和地心地固系上的位置矢量。
为简化计算,将地标位置的推算放在地心地固系e下进行,显然,地标在地心地固系上的位置是不随时间变化的,有:

合并式(2)(3),将系统状态模型简写为:

其中,w(t)为系统噪声阵。
2.2 量测模型
设航天器对地三轴稳定,航天器本体坐标系b与相机系c重合,将采样地标相对于航天器的视线矢量l作为量测值,为描述该视线矢量,建立视线坐标系s,如图3 所示。视线坐标系s由航天器本体系b先后绕Zb及Yb旋转获得,Zs指向视线方向。此时量测值ls=[0 0 1]T,其中lsz为视线矢量在视向系z轴的分量,不包含量测信息,在仿真计算中可省略,该过程可有效减少滤波时量测方程的维数,提高计算效率。

图3 坐标系示意Fig.3 Schematic diagram of coordinate system

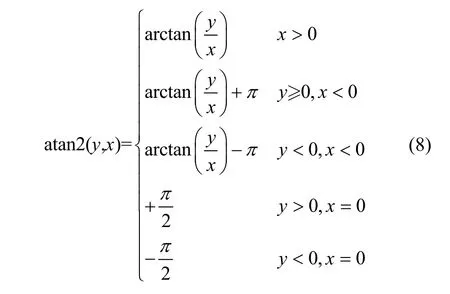
式(6)建立了视线坐标系s与惯性系i的转换关系,对当前采样地标相对于航天器的视线矢量,有如下几何约束:


图4 未知地标与在轨航天器几何关系Fig.4 Geometric constraints of unknown landmarks and spacecraft in orbit
式(6)的量测模型,可简写为:


值得一提的是,由于跟踪的地标数目是动态变化的,故量测量、状态量、协方差矩阵等应根据所跟踪地标个数变化而进行相应的维数处理。
3 未知地标提取及跟踪
3.1 未知地标提取
新增地标位置是未知的,对于待跟踪的所有地标点,其位置初值由从图像中提取的视线矢量与地球的交点近似获得初值,并在跟踪过程中持续估计。
为了建立地标与航天器的联系,首先要在获取的光学图像中提取具有一定特征、且易于跟踪的地标点。本文使用Shi-Tomasi 检测算法进行地标点的提取,该算法是Harris 角点算法的改进算法[7],用于提取图像的强角点。
Shi-Tomasi 算法通过计算自相关矩阵M来描述一个点是否为角点,设灰度图像在点(x,y)处的值为I(x,y),以该点为中心建立搜索窗口O,分别用I x,Iy表示灰度在横纵方向上的偏导数,定义自相关矩阵M:其中,w(x,y)为位置(x,y)处的窗口函数,表示窗口内各像素的权重,本文将窗口内所有像素的权重均设为1。
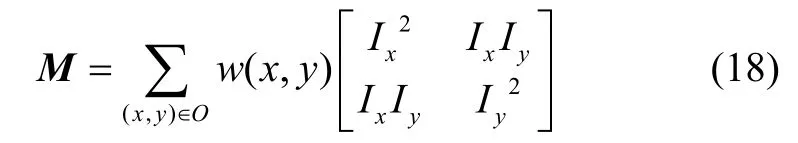
将M的特征值与设定的阈值进行比较,大于该阈值则确定为角点。Shi-Tomasi 角点具有稳定性好、不易受到运动变化和外界噪声的影响等优良特性。
确定待跟踪的地标点后,可通过式(6)(7),使用地标像素坐标提取地标相对航天器的视线矢量,结合航天器的概略位置,可求得地标在地固系上的估计值,将此估计值作为地标位置初值。对于地球的椭球模型,本文使用WGS84 协议椭球参数,固连在地球上的地标有如下约束:

其中,A、C分别为赤道半径和两极半径,根据视线矢量li建立直线方程:

其中,ri为采样时刻航天器在惯性系下的位置估计值,k为地标与航天器的距离。联立式(19)(20),有:

其中,lix、liy、liz为视线矢量在惯性系下的三轴投影。由式(21)可求得k的两个解,取其中的较小值,即可根据式(20)获得距离航天器位置更近的点作为地标位置的解pe。
3.2 未知地标跟踪
在第一帧图像中获取地标时,初始化时刻的地标视线矢量是标称视线矢量,由于光学跟踪算法的限制,很难保证在随后帧跟踪确定的特征点与第一帧中的特征点一致,该误差导致的视线矢量误差是导航系统主要误差源。对于地标跟踪算法,要求速度快、精度高。
光流法是时下应用于运动目标检测与跟踪技术的主流方法[8]。对于采样地标点与不断传入的新帧,为满足导航需求,导航系统对地标的光学跟踪拥有精度高、耗时短的要求。本文采用LK 光流法进行特征点的跟踪。
光流是物体在空间中运动时,于观测成像面上的像素运动的瞬时速度。LK 光流法是一种两帧差分的光流估计算法[9],该算法基于三个假设:亮度恒定、连续的小运动、空间一致,目标点领域内所有像素的光流d=[u v]T可由式(22)所示方程组求解:

其中,A、b定义如下:

在传统的SLAM 任务中,由于物距较短,特征点更新快,光流法本身特性导致的累积误差微乎其微,对于物距数百公里的航天器自主导航任务,亚像素级的跟踪误差意味着地固系上数十米的偏差,光流法的累积误差不容忽视。
为降低累积误差,在对每帧地标点xt进行光流跟踪后,使用跟踪后的点xt+1对前一帧进行回溯跟踪,求得回溯到前图像的跟踪点,计算回溯点与前一帧的标称点的欧式距离,定义为回溯偏差(Retrospective Bias,RB),记作δ x:
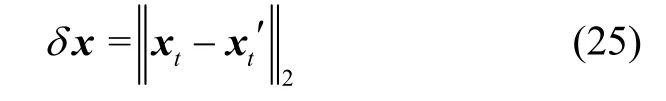
以像素为单位,设定合适的回溯偏差阈值,超过回溯偏差阈值的点做剔除处理,未超过则保留。
4 系统可观性分析方法
对于在第二节建立的未知地标导航系统,该系统是离散非线性时变系统,对系统进行分段定常简化,其可观测矩阵[10]为:

对任意导航时刻k,若可观测性矩阵O满秩,即 det(O)=6+3×n,n为当前跟踪地标总数,则称系统在k时刻可观测。
本文使用O的条件数作为系统可观测度衡量标准,条件数定义如下:

式中,σmax、σmin分别为O的最大和最小奇异值。条件数值越大,矩阵越趋于病态[11],越接近于1,系统定轨性能越优越。
5 仿真实验与分析
5.1 仿真条件
本文以对地定向三轴稳定的卫星进行仿真验证,标称轨道数据由卫星系统工具包(Systems Tool Kit,STK)生成。卫星的轨道六根数设置为:高度300 km、偏心率 0,轨道倾角 70 °、近地点幅角0 °、升交点赤经205 °、真近点角-30 °。
标称遥感成像数据以 STK 的可视化模块(Visualization Option,VO)进行生成,相机光轴指向地心,视场角α为 60 °,成像大小为700 px×700 px,其像元分辨率约500 m×500 m,图像采样频率为1 Hz,固定每一帧图像至多同时跟踪6个随机地标,如图5 所示,使用3 层金字塔LK 光流跟踪[12]。EKF 滤波周期为1 s,仿真时长2000 s。
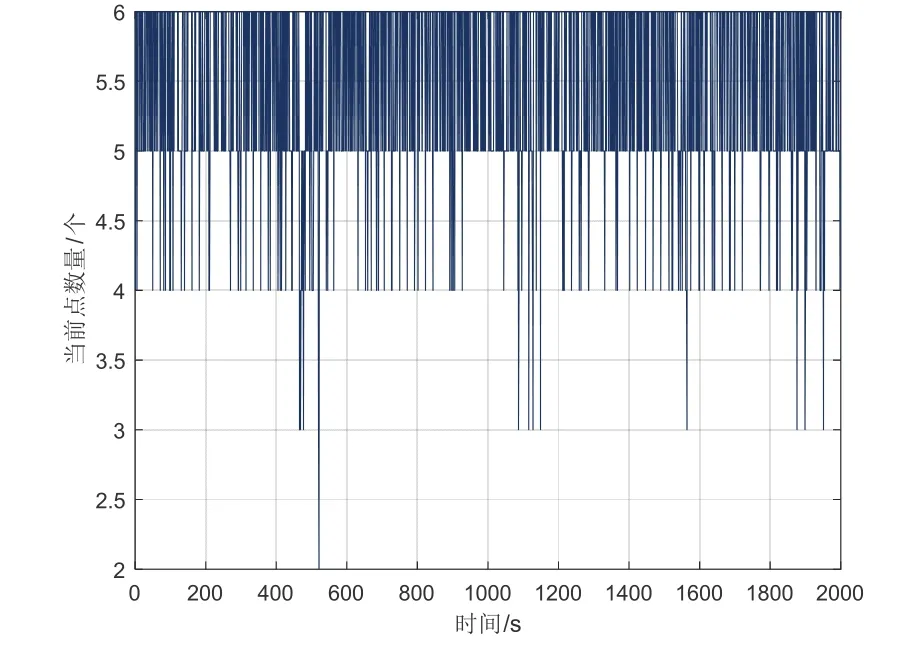
图5 跟踪地标个数Fig.5 Number of tracked landmarks
5.2 地标跟踪及跟踪精度
由于地球并不是一个平面,且卫星在轨运行时,地球也存在自转,地标点在帧序列中的瞬时速度取向并不一致,图6 为实验中某帧瞬时光流场。

图6 瞬时光流场Fig.6 Instantaneous optical flow field
为使地标点在图像中分布均匀,以提高系统可观性,限制所选角点间的欧式距离,对角点间欧式距离做阈值处理,图7 为处理后部分帧序列的光流轨迹。

图7 阈值处理后的光流轨迹Fig.7 Optical flow trajectory after thresholding
跟踪误差指当前跟踪像元与初始化像元时的偏差,将之投影到地心地固系e即为地标跟踪误差,光流跟踪误差直接导致了视线矢量的误差。本文结合STK 设计了一套使用LK 光流法进行地标跟踪的评价方案。使用卫星位置真值Si,根据式(22)计算图像中指定像元在地心地固系e上的位置真值Pe,与下一帧使用跟踪点图像坐标计算的地标位置′比较,用差值描述光流法跟踪精度。
在2000 s 仿真时长中,累积跟踪1930 个地标。针对单个地标,在其采样生命周期中,每两帧之间的跟踪误差均值为8.327 m,标准差3.633 m,投影到卫星本体系则对应均值0.0032 °的测角误差,如图8所示。

图8 帧间跟踪误差Fig.8 Interframe tracking error
显然该跟踪误差在像元分辨率为500 m 的遥感数据前是可喜的。统计所有地标的跟踪时长及对应跟踪误差,发现光流跟踪的误差随跟踪时长的增加而递增,绘制如图9 所示的地标跟踪误差曲线,在跟踪时长超过37 s 时,平均累积跟踪误差达到100 m,显然,这将直接影响到卫星的导航精度。

图9 跟踪误差累积趋势Fig.9 Track error accumulation trend
在3.1 节中提出了回溯偏差RB 的概念,设定回溯偏差阈值为0.003px 以降低跟踪误差。绘制单个地标在地心地固系e上的累积跟踪误差,地标跟踪时长及误差分布如图10 所示。相较于未设定回溯偏差阈值的跟踪方法,使用了回溯偏差阈值的方法后,地标跟踪时长主要分布从40-45 s 降低至5-23 s,累积跟踪误差均值由130.3831 m 降至41.4228 m。

图10 设定回溯偏差处理后的地标跟踪时长及误差分布Fig.10 Landmark tracking duration and error distribution after RB threshold is set
5.3 基于LK 光流法的航天器未知地标导航精度
在上述仿真条件下,设定卫星位置初值误差为15000 m,速度初值误差为5 m/s,进行导航解算的计算机仿真,图11-13 分别展示了卫星的三轴位置误差、三轴速度误差,以及地标在地心地固系e上的三轴位置误差仿真结果。
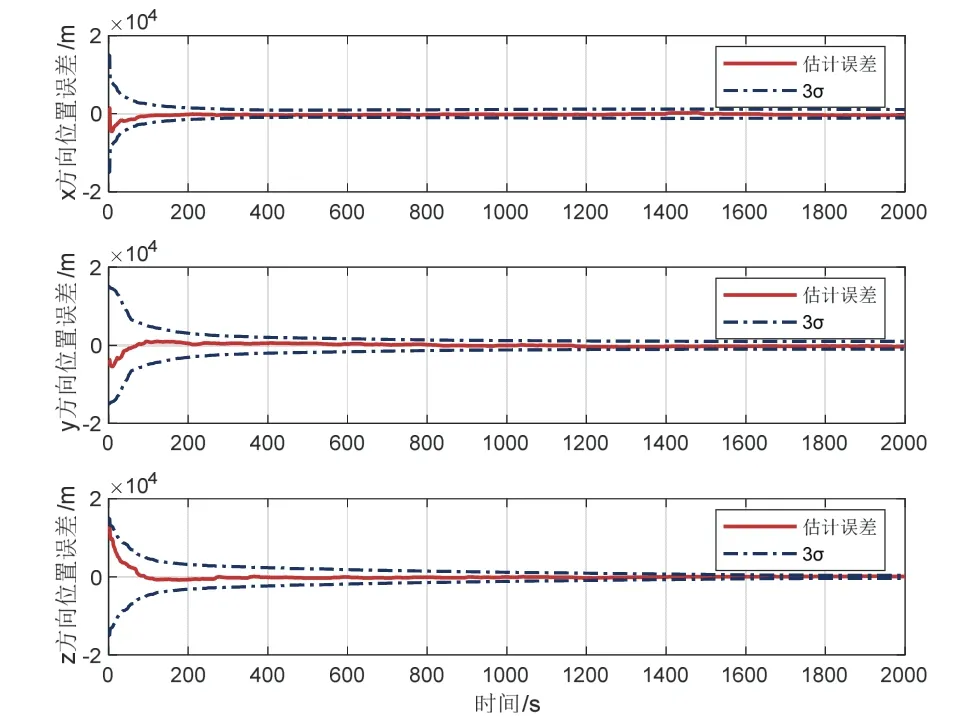
图11 卫星位置估计误差Fig.11 Satellite position estimation error
未知地标导航系统滤波300 s 收敛后,卫星位置均方差为402.67 m,速度均方差为0.481 m/s,最大速度误差为0.7737 m/s,对地标的位置估计均方差为679.88 m。
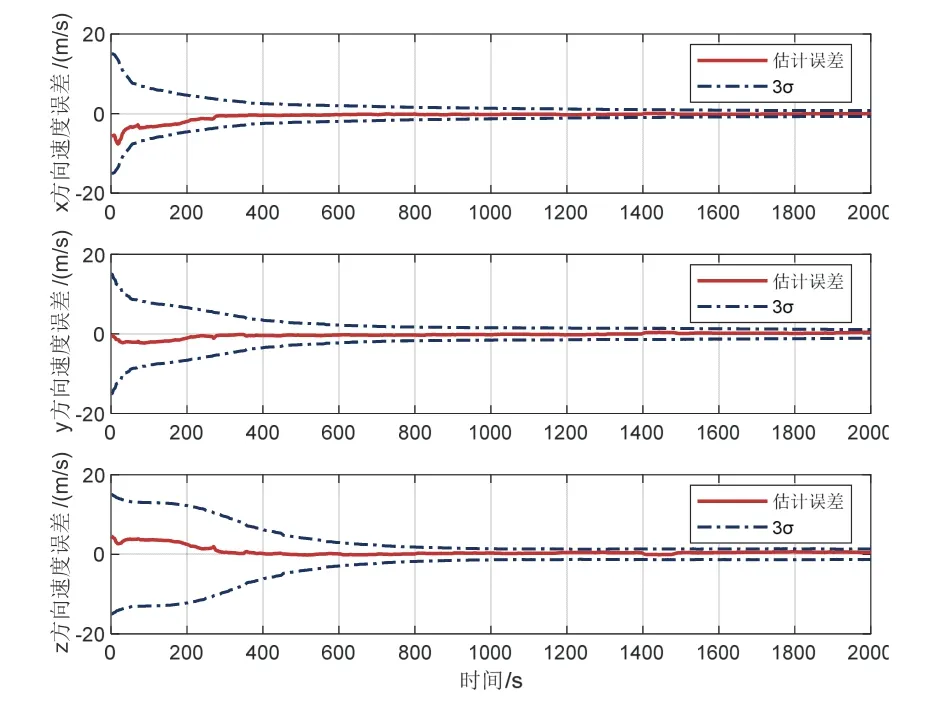
图12 卫星速度估计误差Fig.12 Satellite velocity estimation error

图13 地标位置估计误差Fig.13 Landmark position estimation error
5.4 系统可观测性分析
对于航天器未知地标导航方法,系统的状态方程和观测方程可由式(5)(11)得到,当地标数量为1 时,设在k时刻有系统状态估计值=[1648728 4206374-4.703571 727.7 -5634.1 -5376.1 -4464936 -728397-4496043],在上述仿真条件下,k时刻O的秩rank(O)=9,说明在地标数为1 时该系统即可观测,在观测过程中,整个仿真过程中系统的可观测度均值为553.53,即地标数为1 时,系统持续可观测。
图14 为在500 s 仿真过程中,同时跟踪不同数目地标时系统可观测矩阵的条件数,可见系统的可观度随着跟踪地标数目的提高而提升。
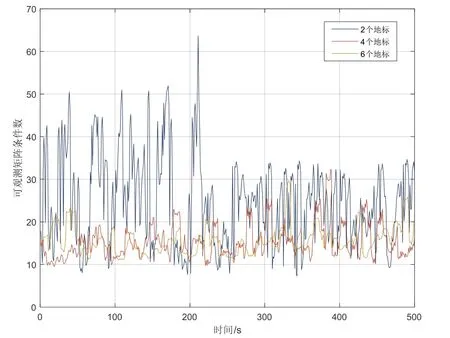
图14 跟踪不同数量地标时的系统可观测度Fig.14 The observability when tracking different number of landmarks
5.5 不同轨道高度的跟踪及定位性能对比
针对上述实验,本文做了进一步地分析和比较,分别使用轨道高度为120 km、230 km、300 km、400 km 和560 km 的卫星进行仿真验证,仿真结果如表1 所示,列出了对应的地标跟踪误差、视线矢量误差及卫星的位置、速度误差。

表1 不同轨道高度的仿真结果Tab.1 Simulation results for different orbit height
由表1 可知,依靠对地标光学跟踪的自主导航方法在低轨道体现了较大的优越性。随着轨道的升高,地标在视场中的跟踪时长也随之变长,视线矢量累积误差也随之提高,系统导航精度降低。考虑设计更先进的、不随时间增长而累积误差的光学跟踪办法,将是后续研究的重点。
5 结论
本文针对对地定向的三轴稳定卫星,使用LK 光流法对遥感图像序列进行处理,设计了一种基于未知地标的航天器自主导航系统,为使用遥感图像进行卫星自主导航提供了新思路。仿真实验结果表明,在使用较低分辨率的遥感图像(500 m×500 m)的情况下,该方案也拥有较快的收敛速度与较高的导航精度。
