高速公路封道施工路段交通流特性及通行能力分析——以杭州湾大桥内侧两条车道封道情形为例

王梓杰 ,祝会兵* ,叶岳定 ,杨 斌 ,肖 龙

（1.宁波大学 土木工程与地理环境学院,浙江 宁波 315211;2.宁波实华原油码头有限公司,浙江 宁波 315812;3.宁波杭州湾大桥发展有限公司,浙江 宁波 315001）

在高速公路中设置施工区,往往会增加车流的交织冲突,容易引发交通拥堵,甚至发生交通事故,因此高速公路施工区具有明显的瓶颈效应,对车辆正常行驶造成严重影响,也使得研究高速公路封道施工时的交通流特性及通行能力具有重要的实际意义.

交通流建模是研究交通流特性最有效的方式之一,元胞自动机交通流模型[1-5]由于其离散性的特点,可再现许多实际的交通现象,因此被广泛应用于道路交通流特性研究中.Nagel 等[1]提出的NaSch 模型是经典的元胞自动机模型之一,能够描述一些实际的交通现象,比如自发产生的拥堵以及“时走时停波”等现象.Dailisan 等[5]在NaSch 模型的基础上,建立了包含公交车和小车的混合车辆交通流模型.

正是由于元胞自动机有许多优点,因此许多学者在研究高速公路封道时也采用这种方法.Das等[6]利用元胞自动机交通流模型模拟施工区交通流,发现施工区的存在不仅造成封闭车道上的交通堵塞,而且在旁路车道上也会产生堵塞.Meng等[7]研究了施工区路段司机的加减速行为,通过建模研究了施工区的交通延误[8],同时还研究了速度与流量的关系以及车辆的合流行为[9],并且得到了交通流速度随施工区数量、长度和大型车辆比例的变化情况[10].Fei 等[11]分析了各种情况下车辆的合流概率、流量-密度关系、车辆时空演化规律以及换道率,推荐了合理的合流区长度和车辆限速值.然而,随着施工规范越来越精细,现有模型对于施工区域的划分大都不够细致,对实际建模场景中车辆的运动状态描述也不够准确,在真实再现施工区交通流特性方面还有待完善.

此外,通行能力是一个重要的交通流特性指标,在高速公路中,通行能力越大,交通运输的效率就越高.黄晓迪[12]通过提出多个指标判断高速公路拥堵状态,选取相应的权重计算综合度量指标,并确定具体的通行能力值.史盛庆等[13]根据有关规范标准,明确了高速公路实际通行能力的计算方法.此外,在进行封道施工时,道路的通行能力会有明显下降,因此封道施工时的高速公路通行能力也是众多学者的研究热点.邵长桥等[14]结合实测数据和仿真实验,量化了施工区通行能力的影响,给出了不同条件下的通行能力推荐值.陈卫霞等[15]针对四车道高速公路超车道封闭施工区的交通流特性,利用车头时距分布的Erlan 模型,发现从上游正常路段至警告区再至施工区的道路通行能力逐渐降低.熊师远等[16]分析了多种因素对施工路段的通行能力影响,确定了施工路段实际通行能力评估指标体系及评估标准.

但是,上述研究均未涉及基于交通流建模的基准通行能力计算,也没有结合道路服务水平的分析推荐合理的极限流量值,以保证施工路段的交通顺畅.

为此,本文以三车道杭州湾跨海大桥路面交通流为研究对象,建立了内侧两条车道封道时的交通流模型,分析道路施工路段对交通流造成的影响,并且在建模基础上研究道路通行能力,同时参考现有规范分析高速公路施工路段的服务水平,提出了具体的流量管控极限值,为杭州湾跨海大桥交通管理部门提供理论参考.

1 交通流实测数据统计分析

杭州湾跨海大桥连接宁波市和嘉兴市,是沈海高速(G15)的重要组成部分.交通流实测数据来自杭州湾跨海大桥上的交通摄像资料,首先选取2020 年10 月15 日7:00—19:00 无封道情况下宁波方向的视频资料进行统计分析,如图1(a)所示,I-I截面与II-II 截面相距152 m.统计I-I 截面三条车道上的车辆数,并区分大小车辆,得到各条车道的流量和大车比例.另外,可以得到车辆通过两个断面的时间,从而计算出车辆速度.统计结果表明,道路流量值随时间有一定波动,最大值为1 585 辆·h-1,三条车道流量比约为3:3:2;大车比例约为0:0.3:0.7,且道路上总大车比例在0.3 左右.大桥上限速100 km·h-1,在三条车道中,第一车道平均车速最大,为95.28 km·h-1,第三车道平均车速最小,为84.64 km·h-1.

为研究内侧两条车道封道时的交通流特性,本文选取2022 年6 月16 日9:00—20:00 内侧两条车道封道时的录像资料进行统计分析,如图1(b)所示.采取相同的方法得到流量、大车比例和车速.道路的整体大车比例仍为0.3,整体流量变化幅度不大,流量高峰为1 250 辆·h-1.此外,施工区路段的限速为60 km·h-1,大部分车辆的平均速度在限速值以内,但是仍存在超速车辆,且大部分为小车.

图1 交通流实测路段示意图

对比两种情况的交通流参数,发现道路总体的大车比例都在0.3 左右,道路流量高峰都出现在上午10 点左右.但无封道时的流量高于内侧两条车道封道时的流量,并且无封道时的平均车速明显高于封道时的平均车速.由此可见,三车道高速公路在内侧两条车道封道时,流量与速度都会受到很大影响.

实测数据可以直观展现交通流的宏观特征,但不能深层揭示交通拥堵的成因等特性,因此还需要利用交通流模型对内侧两条车道封道时的交通流展开研究.在数值模拟中,第一至第三车道的进车率比例以正常路段的流量比作为参考,设置为3:3:2,三条车道的大车比例设置为0:0.3:0.7,而总体的大车比例为0.3.

2 封道施工时交通流模型的提出

在现代交通流的研究中，许多模型都是基于实测的交通流数据[14,17-18],本文也采用相同的方法,基于实测资料建立杭州湾跨海大桥封道施工时的交通流模型.

2.1 施工路段的道路设施

以杭州湾跨海大桥内侧两条车道封道时的情形为例,道路交通如图2 所示.根据《公路养护安全作业规程》[19],封道路段除正常路段和施工路段,还设置警告区和终止区.本文为便于描述车辆的运行状况,在建立的模型中将道路划分为正常路段、警告区、合流区、施工路段和终止区.

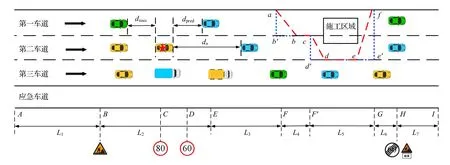
图2 杭州湾跨海大桥内侧两条车道封道时道路交通示意图

首先,车辆从左侧边界驶入,进入正常路段AB,长度为1L,正常限速要求100 km·h-1,但实际上小车限速100 km·h-1,大车限速80 km·h-1.接着是警告区BE,长度为2L,B点处有警示标志牌,下游有两次限速变换,分别在C点和D点,C点限速值为80 km·h-1,D点限速值为60 km·h-1,这样BE 段细分为三部分,即BC段、CD段和DE段,长度分别为l1、l2、l3,所以警告区BE段总长L2=l1+l2+l3.

再看施工路段.虽然真正的施工区域如图2 中的黑框区域,但在规范中第一、二车道封道形状为“阶梯”状,即长虚线abcdef所包围部分.所有车辆都需要绕过其间,从第三车道通过施工路段,限速为60 km·h-1.为便于建模,将封道路段设置成图中短虚线ab′c d′e′f形状.所以,第一车道封道长度为FG,而第二车道封道长度是F′G.本文在警告区与施工路段间设置一个合流区,第一车道的合流区是EF段,长度为L3,第二、三车道的合流区是EF′段,长度为L3+L4,车辆限速仍为60 km·h-1,该区域上的车辆会尽可能换道至第三车道,以便通过施工路段.施工路段的下游是终止区GH,长度为L6,H点为终止区终点,也是正常路段的开始点,通过该点以后,车辆恢复正常路段的限速.HI路段又恢复为正常路段.

2.2 内侧两条车道封道时的交通流模型

建立内侧两条车道封道施工时的元胞自动机交通流模型,采用开放式边界条件[20],如图3所示,即在每条道路的左侧边界设置长度为vmax+1的进车区域,这里vmax为车辆能够达到的最大速度,为无量纲数.在每个时间步内,识别道路上靠近左边界第一辆车所在位置x1,若x1＞vmax,表示进车区域无车,这时就以进车概率α进入一辆车.而当车辆行驶至右边边界时,以概率β驶出道路出口,否则以概率(1-β)在右边界停车等待,成为上游车辆的障碍;特殊地,当β=1时,即开口边界为全开放.判断车道上最前面一辆车所在位置,如果该辆车的位置大于道路系统的总长度,那么就认为该车已驶离本车道,将这辆车消除.

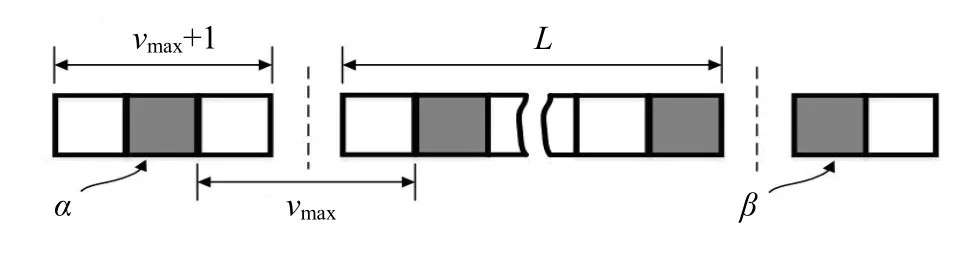
图3 开放式边界示意图

取道路总长L=4 200,每个元胞长度为1 m,则道路总长为4 200 m,同时每个时间步长取为1 s.模型中有两种车型(大车和小车),它们具有不同的最大速度、加速度和长度.同时,在模型中考虑司机性格差异,将司机分为谨慎型司机和激进型司机,其中激进型司机占25%[21].取第一车道封道路段FG总长为1 000 m,第二车道封道路段F′G总长为550 m.正常路段AB长度为1 000 m,警告区BE总长为1 000 m,其中BC为500 m,CD段为250 m,DE段为250 m.第一车道合流区EF段长度为500 m,第二、三车道合流区总长为EF和FF′段之和(L3+L4),FF′段对应规范中上游过渡区,取450 m,故EF′段总长为950 m.终止区GH段长度为50m,正常路段HI长度取为650 m.

在模拟中,每个时间步车辆位置同步更新一次,为消除暂态影响,前10 000 个时间步运算不计入计算结果,后10 000 个时间步的计算结果作为模拟结果.交通流模型包括车辆纵向前进规则和横向换道规则两个部分,分别叙述如下.

2.2.1 车辆纵向前进规则

车辆纵向位置更新规则采用DHD 单车道元胞自动机交通流模型[22]的有关规定,区分激进型司机与谨慎型司机的性格特点,分别遵循不同的前进规则.激进型司机驾驶的车辆纵向位置更新规则表达如下:

其中,vn(t)、vn(t+1)分别指当前车在t时刻和下个时刻的速度;xn(t)和xn(t+1)分别表示当前车在t时刻和下个时刻的位置;指小车所能达到的最大速度;指前车的预期速度;dn(t)是车间距,即dn(t)=xn+1-xn-l,其中,xn+1和xn分别是前车与当前车辆的位置,l是车辆长度,这里区分小车与大车的车辆长度;dn+1(t)是前车与其前面车辆的车间距;ac表示小车加速度,区分行驶状态与起步状态的加速度,分别取1 m·s-2和3 m·s-2.

谨慎型司机驾驶的车辆纵向位置更新规则表达如下:

(1)加速:vn(t+1)=min(vn(t) +a,vmax);

(2)减速:vn(t+1)=min(vn(t),dn);

(3)以延迟概率P随机慢化:vn(t+1)=max(vn(t) -a,0);

(4)位置更新:xn(t+1)=xn(t)+vn(t+1).

谨慎型司机驾驶的车辆有大车也有小车,加速度区分小车加速度和大车加速度,也区分行驶状态与起步状态的加速度,大车分别取1 m·s-2和2 m·s-2,小车加速度取值同前.vmax表示当前车辆允许达到的最大速度,区分大车与小车,小车所能达到的最大速度取28,对应杭州湾大桥上的限速值100 km·h-1,大车的最大速度取22,对应实际车速80 km·h-1.

2.2.2 车辆横向换道规则

根据车辆行驶特点,在正常路段以外,不同区域上车辆的换道行为都有所不同.这里,将每个区域的换道规则分别表述如下.

(1)正常路段车辆换道规则.正常路段是指封道作业区域以外的路段,即图2 中的AB段和HI段,车辆的换道规则采用MR-STCA 元胞自动机交通流模型[21]的换道规则,区分激进型司机与谨慎型司机的驾驶行为差异,分别表达如下:

1)激进型司机

部分驾驶小车的激进型司机通常喜欢追求理想驾驶速度,一般换道较为频繁,其换道规则为:

①换道动机:

式(1)表示车辆在下一时刻的车间距无法满足加速时需要的条件,而目标车道的驾驶条件比当前车道要好.式(2)中,dpred表示当前车辆与目标车道前车的车间距;vpred表示目标车道前车在下一时间步的预期速度.如果满足上述两个条件,激进型司机就有换道的愿望.

②安全条件:

式中:dsucc表示当前车辆与目标车道后车的车间距;vsucc表示目标车道后车在当前时间步速度;vs,max表示目标车道后车可能达到的最大速度.式(3)表示目标车道后车与本车的车间距大于后车在下一时间步可能达到的速度,这保证了车辆在换道时不会产生碰撞.

2)谨慎型司机

谨慎型司机包括所有大车司机及一部分小车司机,换道时比较保守,因此本文基于Chowdhury等[2]提出STCA 模型中的换道规则:

①换道动机:

②安全条件:

其中,加速度a和最大速度vmax根据车辆类型的不同而取不同值;dsafe表示车辆应保持的安全距离,这里是目标车道上后车可能达到的最大速度;其他参数同上面所述.

(2)警告区车辆换道规则.图2 中的BE段是警告区.该路段采用对称换道,区分激进型司机与谨慎型司机,整体的换道规则表达如下:

1)激进型司机

①换道动机:

其中,L1、L2如图2 中所示,式(7)表示车辆处于警告区;式(8)中表示第一、二车道警告区的车辆换道至目标车道所需预留的最小空间,即当前车辆与目标车道前车的车间距,本文取=14.

②安全条件:

其中,dsucc是车辆与其目标车道上后车的车间距,vsucc是目标车道上后车的速度,式(9)表示车辆与目标车道后车的距离大于其速度,保证车辆不会碰撞.

2)谨慎型司机

换道规则与正常路段谨慎型司机的换道规则相同.

(3)合流区车辆换道规则.图2 中第一车道EF段和第二、第三车道EF′段为合流区.合流区的设置是为了内侧两条车道上的车辆在施工区域前能尽快地换道至第三车道,司机会采取比警告区路段更激进的换道行为,而且是非对称换道,也就是车辆只是由第一车道向第二车道换道、第二车道向第三车道换道,换道规则表达如下:

1)激进型司机

①换道动机:

第一车道:

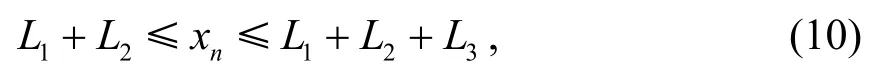
第二车道:

其中,L1、L2、L3、L4如图2 中所示,式(10)、(11)表示车辆处于两个车道各自的合流区;dpred表示车辆与目标车道前车的车间距,取=7,式(12)表示车辆有足够的换道空间.

②安全条件:

2)谨慎型司机

换道规则与正常路段谨慎型司机的换道规则相同.

(4)施工区车辆换道规则

施工区内侧两条车道封闭,即图2 中F G′ 路段,此时车辆只能行驶在第三车道,不存在换道行为.

(5)终止区车辆换道规则

在终止区,内侧两条车道解除通行限制,车辆又可以换道进入内侧两条车道行驶,此时各个车道上车辆的换道规则与正常路段相同.

3 模拟结果分析

3.1 模型验证

选取内侧两条车道封道时上午9 点到晚上8 点的交通流实测数据进行统计分析,以5 min 为单位对流量和速度值取平均,即1 h 得到12 个时段平均数据,共计11 h,得到132 个时段的流量和速度值,将其转化为小时流量和小时速度,绘制成流量—时间序列图和速度—时间序列图,分别如图4(a)、(b)所示的圆形数据点.同时,假设在施工区终点,即图2 的G断面处安装一个虚拟探测器,利用建立的交通流模型,将实测流量换算成进车率,作为模型参数,模拟每5 min 通过G断面的平均流量和平均速度,调整进车率,模拟得到从上午9 点至晚上8 点共132 组流量和速度值,同样画出流量—时间序列图和速度—时间序列图,如图4(a)、(b)中三角形数据点所示.

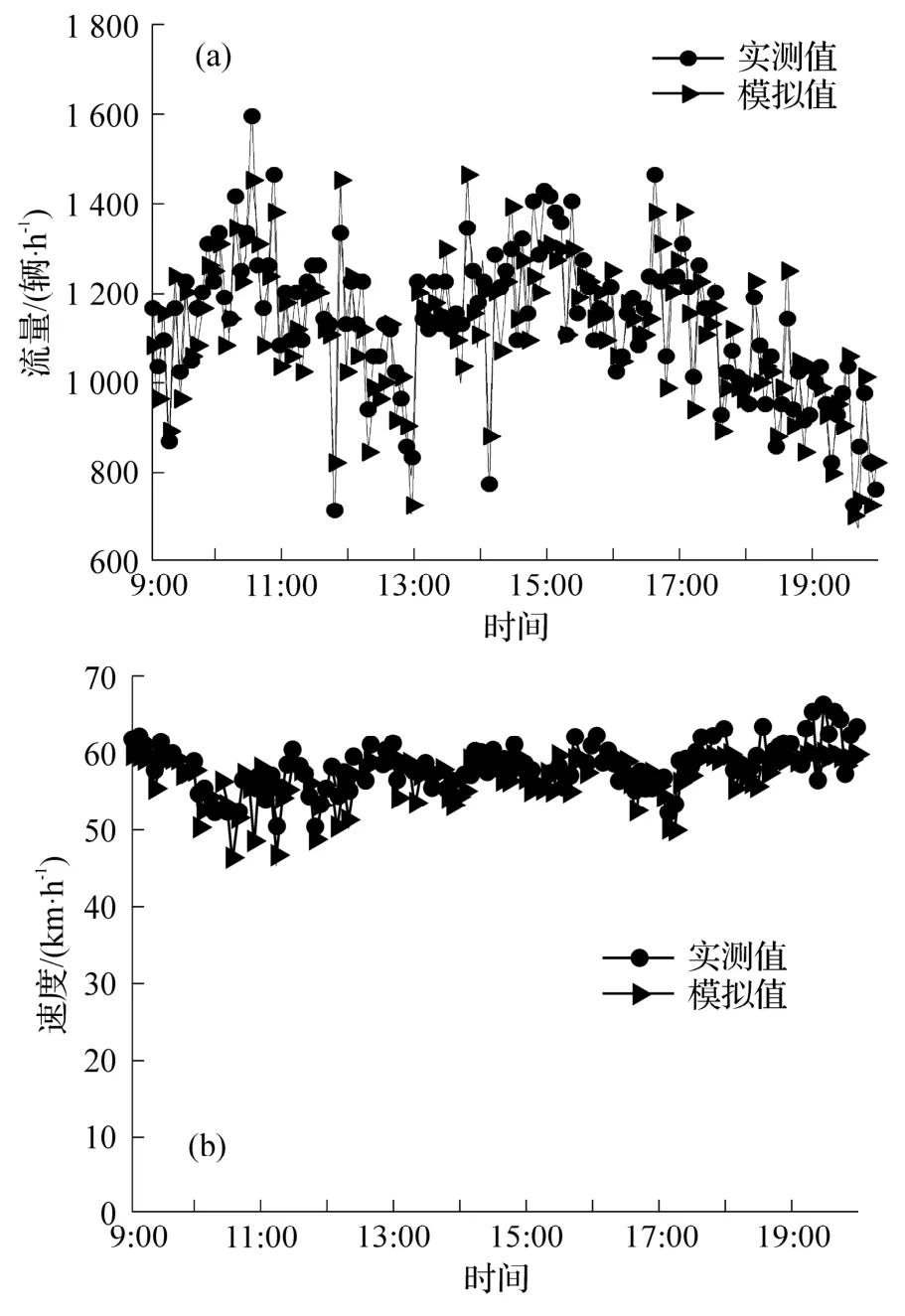
图4 模拟流量及速度值与实测数据对比图

由图4 可以看出,模拟的流量和速度值与实测数据基本吻合,只是部分实测车速有超过施工区限速60 km·h-1的超速情况,而模型中由于没有考虑超速车辆的存在,因此存在偏差.由此可以得出,模型能基本有效地再现内侧两条车道封道时,车辆通过施工区的交通流情况.

3.2 封道路段交通流特性的模拟与分析

在内侧两条车道封道时,利用提出的交通流模型计算了不同进车率情况下的车辆平均速度,结果如图5 所示,同时作为比较,计算未封道时的车辆速度.图中进车率α1是第一车道的进车率,从实测数据分析中得到第一、二、三车道的进车率关系为α1:α2:α3=2:2:3,进车率也代表了车辆密度,实际上,横坐标间接反应了全部三条车道的进车率.

图5 封道时车辆平均速度随进车率的变化图

从图5 中可以看到,由于受到封道施工期间限速60 km·h-1的影响,任何进车率下,内侧两条车道封道时,车速均低于未封道时的情形,只是在进车率α1为0.1 左右时,两者差异稍小,说明在低密度时,封道施工对车辆的正常行驶影响稍小.随着进车率的增大,封道与未封道时的速度均有所下降,但封道时速度下降幅度更大.当进车率α1≥0.7 时,此时未封道的平均速度为70 km·h-1左右,而内侧两条车道封道时的平均速度仅为35 km·h-1左右,可见,当密度较大时,内侧两条车道封道对道路交通产生了严重影响.

为了细致研究施工路段对车辆行驶带来的影响程度,通过数值模拟,得到了第一车道封道总长为1 000 m,第二车道封道总长为550 m 时的三条车道的时空演化图.如图6 所示,其中,图6(a)为进车率α1=α2=0.25,α3=0.17 时的情形,图6(b)为进车率α1=α2=0.4,α3=0.27 时的情形,分别代表施工路段流量约为900 和1 100 辆·h-1的交通状况.图中横坐标代表路段长度,纵坐标代表时间,从上到下依次代表第一车道至第三车道,一、二车道上的黑色网格代表封道区域,其中第一车道封道长度为1 000 m,第二车道封道长度为550 m.粗点(橙色)代表大车的轨迹,细点(蓝色)代表小车的轨迹.图中上方字母含义与图2 一致.出车率β设置为1.

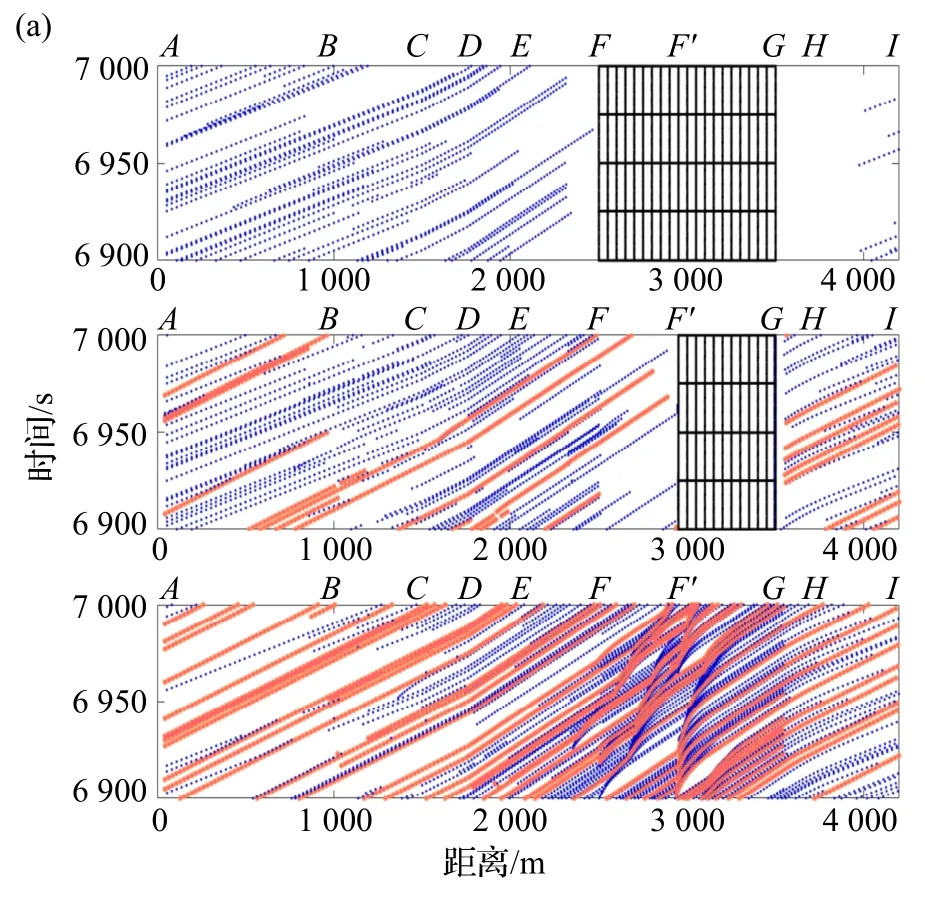
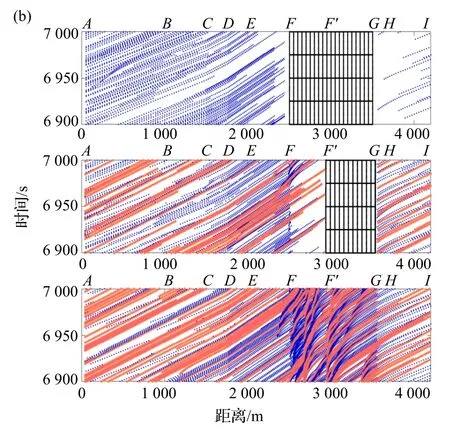
图6 内侧两条车道封道时的车辆时空演化图

可以看到,第一车道均是小车,第二、三车道为小车与大车混合通行,而第三车道大车比例更高,这与交通视频中看到的现象一致.当施工路段流量为900 辆·h-1,如图6(a)所示,时空演化图中车辆的轨迹线较为稀疏,在合流区上游(即AE路段),车辆行驶较为顺畅,没有出现拥堵;同时,第一、二车道上的车辆在合流区终点(分别为F和F′断面)前都能成功换道至第三车道,而第三车道车辆在合流区EF′路段和施工区起点F′断面都有少量时走时停波产生,存在小幅拥堵,但并未对车辆行驶造成较大影响,说明此时内侧两条车道封道对交通流的影响较小.

当施工路段流量为1 100 辆·h-1,从图6(b)可以看到,此时流量有所增加,车辆轨迹线变得更加密集,第一车道合流区EF路段和第二车道合流区EF′路段的车辆明显增多,并且由于有更多的车辆进行换道,第三车道合流区EF′路段上拥堵现象严重,同时轨迹线更陡,说明车辆速度在下降.这也可从图5 中得到印证,在α1=0.40,即流量为1100辆·h-1时,道路的平均速度已有明显下降,其通行能力受到一定影响.

那么,施工区对通行能力的影响是否会随着施工区长度的不同而不同呢？施工区长度是指实际施工区域的长度,在规范中封道长度包括上游过渡区、纵向缓冲区、施工区域和下游过渡区,其中上游过渡区、纵向缓冲区和下游过渡区的总长度有推荐值,在第一车道总长700 m,第二车道总长200 m,本文通过改变施工区域长度从而调整封道总长度.在数值模拟中,第一、二车道上的实际施工区域长度相同,由100 m 开始,并以50 m 为增量逐渐增至1 000 m,则第一车道实际封道总长为800～1 700 m,第二车道实际封道总长为300～1 200 m.通过数值模拟第三车道F G′ 路段流量随施工区域长度及进车率的变化,结果如图7 所示.图中横坐标为第一车道进车率α1,纵坐标为施工区域长度,其不同深浅颜色代表不同的流量值,颜色越浅流量越大,颜色越深流量越小.

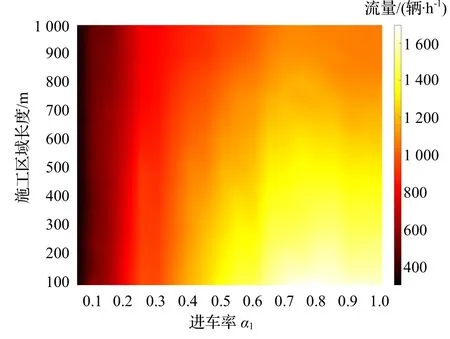
图7 流量随进车率和施工区长度的变化趋势

由图7可见,当α1≤0.2时,通过施工路段流量较小,随着施工区长度的增加,车道总流量并未有明显变化.当0.2＜α1＜0.4 时,在相同施工区域长度时,车流量逐渐增大,但对应于相同进车率,流量随着施工区域长度增大而下降.当α1≥0.4,施工区域长度小于300 m 时,流量可达到1 400 辆·h-1以上,但随着施工区域长度的增加流量逐渐减小,当施工区域长度大于700 m 时,流量会小于1 200辆·h-1.因此,内侧两条车道封道时,在进车率较小情况下,施工区域长短并不会对道路的总流量产生影响,也就不会影响车辆正常行驶.但当进车率大于0.2,即流量大于800 辆·h-1时,随着施工区域长度的增加,道路总流量逐渐减小,从而引起道路通行能力的下降.

3.3 施工区通行能力分析

综合上述研究,施工区的存在会对车辆行驶造成一定影响,如何改善施工区的道路交通状况是值得研究的问题.根据《公路工程技术标准》[23],高速公路的道路服务水平分为6 个等级: 一级和二级服务水平时,交通流处于自由流状态,驾驶员可以按照自己意愿行驶;三级服务水平时,交通流状态处于稳定流,车辆间的相互影响变大;四级服务水平时,速度和驾驶自由度都受到明显限制,流量稍有增加,服务水平就会显著降低;五级和六级服务水平时,交通流往往出现明显拥堵,车辆排队行驶,运行状态极不稳定.

通常,Q/C值是评价道路服务水平的指标,其中,C为基准通行能力,单位是pcu·(h·ln)-1,即每小时每车道的当量车流量,本文取无大车时最大流量为基准通行能力[24].在模拟时,第一车道封道总长为1 000 m,第二车道封道总长为550 m,得到基准通行能力值为1 851 pcu·(h·ln)-1.Q是服务交通量,单位pcu·(h·ln)-1,由于是大、小车辆混合通行,模拟得到的流量需按一定折算系数换算成服务交通量,其中小车折算系数为1,大车为2.5.服务水平等级与Q/C值的关系见表1[24].

表1 服务水平等级与Q/C 值关系

利用交通流模型计算出FG路段在各种进车率下的流量,进而得到各种进车率下的当量流量,即服务交通量,并绘制服务交通量—进车率关系图,如图8(a)所示.根据得到的服务交通量和基准通行能力,计算不同进车率α1时的道路服务水平指标Q/C值,从而得到Q/C值与进车率关系曲线,也绘于图8(a)中.对照表1,划分了6种道路服务水平的进车率区间.同时,计算了不同进车率下FG路段的平均速度,如图8(b)所示.

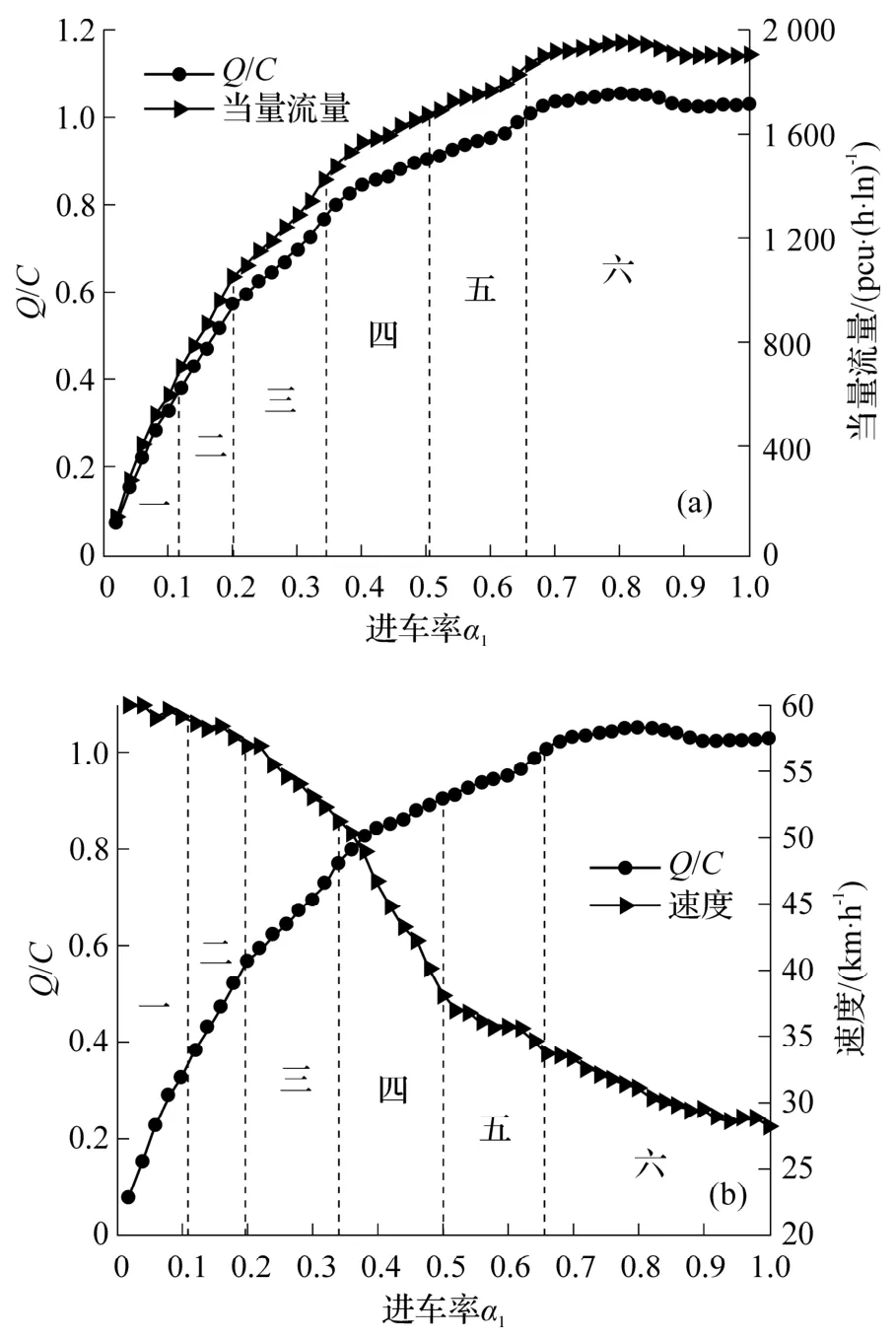
图8 不同进车率与当量流量、Q/C 值及速度的关系

当第一车道进车率α1≤0.2时,流量小于1 100 pcu·(h·ln)-1,平均车速超过55 km·h-1,Q/C≤0.55,道路服务水平在二级以上,此时交通流处于自由流状态,即使存在施工区,车辆依然可以有序行驶,不会出现拥堵.当0.2＜α1≤0.34 时,从图8(a)上可以看到,此时流量区间为1100～1 400 pcu·(h·ln)-1,Q/C值介于0.55～0.75,虽然车辆间的相互影响有所增大,从图8(b)可见此时速度有一定程度下降,但道路的服务水平达到三级,处于稳定流,图6(a)车辆时空演化图反映的是α1=0.25 时的状况,在这个区间,施工区前第三车道上虽有少量车辆集簇,但是车辆仍然可以顺畅地行驶.

当0.34＜α1≤0.5 时,算得流量区间为1 400～1 600 pcu·(h·ln)-1,从图8(a)中看,Q/C值介于0.75～0.90,道路服务水平达到四级,从图8(b)中可以看出,此时速度明显下降至约35 km·h-1,虽然仍处于稳定流,但是车辆之间的影响加剧.从图6(b)的车辆时空演化图中看到,此时α1=0.4,第三车道合流区EF′路段的车辆拥堵现象明显,所以四级服务水平时的车辆行驶受到严重阻碍.而当α1＞0.5,从图8(a)中看到,流量趋于最大值,此时Q/C＞0.90,道路服务水平为五级或六级,从图8(b)中看出,平均速度在30 km·h-1以下,已处于严重拥堵状态,车辆行驶环境较差.

根据上述分析,在高速公路内侧两条车道封道施工时,为减小施工对道路通行能力的影响,应将道路服务水平控制在三级以上.文中第一车道封道长度1 000 m,第二车道封道长度550 m,此时当进车率α1＜0.34,达到三级以上道路服务水平,从图8(a)可见,此时流量小于1 400 pcu·(h·ln)-1.因此,当第一、二车道封闭,第三车道可通行,且封道长度如上述设置值时,建议杭州湾大桥的道路流量控制在1 400 pcu·(h·ln)-1以下.并且当封道长度不同时,可以按照本文方法得到相应的基准通行能力以及不同进车率时的当量流量,从而分析得到极限流量值作为交通管理的阈值.

4 结论

(1)采用开放式边界条件,建立了三车道高速公路内侧两条车道封闭时的元胞自动机交通流模型,并验证了模型的有效性.

(2)在不同进车率时,计算了内侧两条车道封道情况下的车辆速度,并与正常情形时的车速进行比较,发现在进车率较小(即流量较小)时,车速变化不明显,但随着进车率的增大,封道时车辆的速度明显减小,说明内侧两条车道封闭会降低车辆行驶速度.

(3)在进车率较小时,施工区域长度对施工路段的流量影响较小,可忽略不计.但在进车率较大(即流量较大)时,施工区域的存在会使施工路段的流量下降,并且施工区域越长,流量下降越多.

(4)研究了内侧两条车道封道时的道路服务水平,当第一车道封道长度1 000 m,第二车道封道长度550 m 时,计算了施工区域的基准通行能力以及不同进车率时的服务交通量,并划分了六种道路服务水平下的进车率区间,得出此时流量如能控制在1 400 pcu·(h·ln)-1以下，即可保证施工区域交通的畅通.