节段胶拼箱梁静载试验研究
2023-01-26刘小林刘少成
刘小林,刘少成
(1.中铁大桥勘测设计院集团有限公司,湖北 武汉 430056;2.中铁大桥科学研究院有限公司,湖北 武汉 430034)
0 引言
桥梁结构预制节段拼装工艺施工便捷、质量可靠,且机械化程度高、对环境影响小,具有较好的经济效益和美学效果,从而逐渐得到推广。目前国内节段梁预制拼装技术在铁路桥梁中尚未得到广泛应用,已有的研究只是验证了标准预制梁的受力特征,而较少对非标准荷载、非标准节段胶拼预制梁进行研究[1-3]。本文针对某国外铁路项目,其在跨越城市区段均采用高架桥方案,桥梁结构形式为38 m预应力混凝土节段胶拼简支箱梁。这种结构形式在当地使用不多,设计、施工经验并不丰富。为测试预制节段梁在试验荷载作用下的力学性能,检验梁体的施工质量是否满足设计要求,通过在已架设梁体上施加与二期恒载和列车活载等效的荷载,验证节段梁在设计荷载作用下的刚度和抗裂性,检测桥跨挠度和底板应力并与理论计算进行比较,评价桥梁结构在设计使用荷载下的工作性能,确保箱梁结构质量和后期运营安全,为箱梁桥的竣工验收和正常使用提供可靠的技术依据。
1 节段梁基本参数
为确定桥梁在使用荷载作用下的工作性能,通过模拟实际使用状况,在已架设的节段箱梁上进行静载试验。试验梁为单线铁路梁桥,无砟轨道桥面,采用印度设计规范,铁路轨距1676 mm;设计速度为客车120 km/h,货车80 km/h;设计活载为印度32.5 t轴重活载[4]。
节段箱梁梁长37.88 m,计算跨度36.38 m,沿纵桥向划分为12个节段,如图1所示,中间10个标准节段长度为3.25 m,两侧节段长度为2.69 m。梁体截面类型为单箱单室直腹板变截面箱梁,边支座中心线至梁端0.75 m,横桥向支座中心距为3.3 m。箱梁顶板宽8.45 m,箱宽4.8 m,顶板厚22.5 cm,底板厚25 cm,腹板厚35~55 cm。

图1 节段箱梁结构图(单位:mm)
简支箱梁采用M50钢筋混凝土,箱梁钢筋均采用Grade Fe 500 d钢筋,钢绞线采用高强度低松弛钢绞线,公称直径为15.2 mm,弹性模量为195 GPa,抗拉强度标准值为1 860 MPa。
2 静载试验方案
本试验梁为预应力混凝土节段预制拼装简支梁,与国内相关试验规范中适用范围简支梁存在以下区别[5]。
(1)本试验梁为非标准轨距、非标准活载,超出规范限定范围。
(2)设计活载不同于规范附录A中“中—活载、ZK活载、ZKH活载、ZC活载”,不可采用规范中“等效荷载加载挠度修正系数”。
(3)节段预制拼装梁简支梁,由于胶接缝范围钢筋不连续,应力和强度等控制指标与非胶接连接的厂制预应力混凝土简支梁不同,试验中梁体加载标准及抗裂评定标准应与厂制简支梁不同。
(4)节段胶接连接的非标准预应力混凝土简支梁,无法采用规范附录C中“预应力混凝土静载弯曲试验加载计算”计算加载值。
虽然本节段梁静载试验缺少严格的规范依据,但鉴于本次试验目的不同于现行规范,因此针对该节段梁试验方法及加载操作流程参考上述规范进行。
2.1 加载和反力系统
模拟静荷载考虑二期恒载、列车活载,静载试验加载采用等效集中力形式,对称布置。共设置10个加载断面,每个断面2个加载点,测点布置方式为:10排×2点/排=20点。加载点施加在梁体腹板中心线上,等效集中力的施加方式如图2所示。
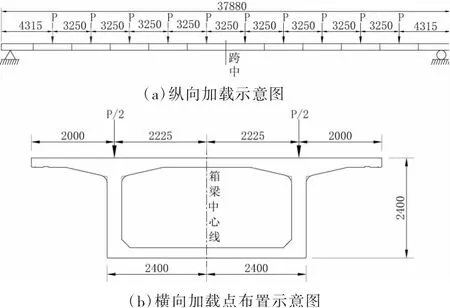
图2 等效集中荷载加载示意图(单位:mm)
开展静载试验的节段箱梁已架设到桥墩上,结合实际结构特点,加载和反力系统采用钢管桩作为地锚,为试验加载提供反力,通过梁体以上的横梁和拉杆,将千斤顶施加的力作用于梁体上,如图3所示,千斤顶沿节段梁跨中对称布置,纵向间距3.25 m,横向间距4.45 m。静载试验加载和反力系统现场布置如图4所示。

图3 加载反力装置布置示意图(单位:mm)

图4 箱梁静载试验加载和反力系统
2.2 挠度测试
梁体挠度测点布置在跨中及梁端支座中心两侧,测量挠度的基准梁与加载系统独立设置。在加载过程中,基准梁不会受到加载和其他任何扰动。整跨节段梁共布置3个监测断面,每个断面2个挠度观测点。梁体挠度测点布置如图5所示。

图5 梁体挠度测点布置
2.3 荷载测试
静载试验采用20点加载法,共配置20个标准测力计用于测试和控制相应千斤顶的试验荷载。测力计的量程为100 t,精度为0.2%F.S,外径ϕ116 mm,内径ϕ75 mm,高100 mm。
2.4 应力测试
箱梁底部应力测试参考规范要求,在跨中截面和靠近跨中区域的梁轴线方向梁底部布设测点[6-7],应变计自跨中截面向两边支座方向两侧梁体底面边缘约2.4 m范围内布置,如图6所示。同时,在跨中拼缝、跨中两侧相邻的两条拼缝处跨缝安装应变计,用于观测试验加载过程中拼缝处的应变变化情况,共安装25个应变计。采用表面式振弦应变计,其安装如图7所示。

图6 箱梁底部应变计布置方式

图7 箱梁底部应变计安装
2.5 裂缝及损伤裂纹观测
由于梁体跨中承受最大弯矩,是最危险且最有可能开裂的区段,静载试验前用放大镜在梁体跨中两侧下缘和梁底面进行外观检查,对梁体既有裂缝进行观察和标记[8]。用放大镜在梁体跨中两侧共8~12 m区段下翼缘及梁底面仔细查找裂纹,对于加载前检查发现的初始裂纹(包括表面收缩裂缝和表面损伤裂缝)及局部缺陷,按约定的方法用铅笔标记。试验过程中,每级加载后仔细检查梁体下缘和梁底有无裂缝出现,如出现裂缝或初始裂缝的延伸,应用记号笔或铅笔标注,并注明荷载等级,量测裂缝长度和宽度。
2.6 静载试验加载程序
为确保混凝土龄期、减小收缩徐变影响,选取试验节段箱梁自预应力张拉完成到开展静载试验间隔天数超过3个月。试验开展参照相关规范和设计文件执行,其中各加载点的设备重量为109 kg,静载试验的最大加载级为1.05级。节段箱梁静载试验的各加载级荷载见表1。

表1 试验各加载级荷载
试验梁的加载分两个循环进行,如图8所示,以加载系数K表示加载等级(加载系数K是加载试验中梁体跨中承受的弯距与设计弯距之比)。试验准备工作结束后梁体承受的荷载状态为初始状态;基数级下梁体跨中承受的弯距指梁体质量与二期恒载质量对跨中弯距及未完成预应力损失的补偿弯矩之和[9]。
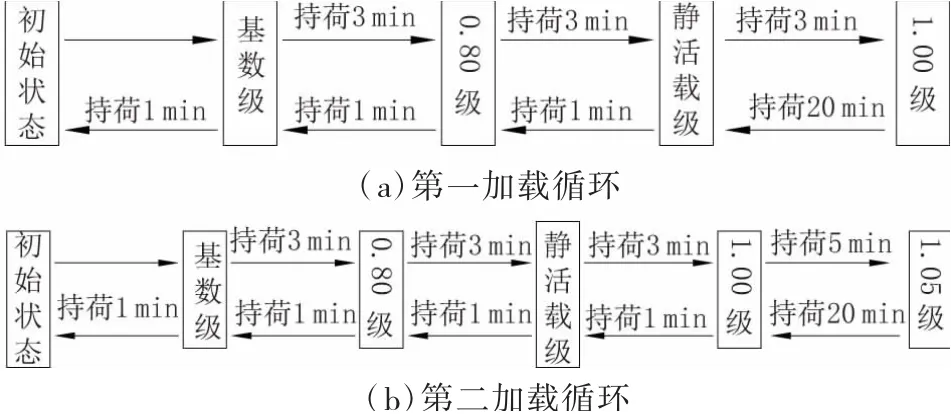
图8 加载循环及持荷时间
3 理论分析
根据节段箱梁结构尺寸和受力特点,采用桥梁有限元通用计算程序建立3D模型,如图9所示,计算桥梁在不同受力工况下的受力和变形。

图9 节段箱梁有限元模型示意图
经计算得到试验节段箱梁在各荷载等级作用下,计算挠度和跨中梁底最大计算正应力值见表2,其中挠度向下为负,正应力受压为正,受拉为负。

表2 节段箱梁计算挠度和最大梁底应力值
4 试验结果分析
4.1 挠度结果分析
每级加载后测量梁体跨中和各支座中心截面两侧竖向位移变化,以同一截面的两侧平均值分别作为相应截面的竖向位移量。跨中截面的竖向位移量减去支座沉降量即为该荷载下的实测挠度值,节段箱梁静载试验实测和计算挠度值见表3。
试验加载过程中,挠度实测值与理论计算值变化趋势基本一致,测点处计算值均大于时间测量值,说明跨中截面竖向挠度变形处于正常状态[10]。由表3实测挠度值可知,第一加载循环静活载挠度与基数级挠度之差为fkb-fka=14.88-5.69=9.19 mm;第二加载循环静活载挠度与基数级挠度之差为fkb-fka=15.45-5.38=10.07 mm。实测挠度值小于理论计算值23.6-10.3=13.3 mm。

表3 节段箱梁实测挠度与计算挠度的比较
参照《简支梁试验方法预应力混凝土梁静载弯曲试验》(TB/T 2092—2018),等效荷载加载挠度修改系数ψ按0.994 2取值,梁的设计挠跨比为1/2 640。第一加载循环静活载作用下挠跨比为f1实测/L(fkbfka)/L=(14.88-5.69)/36 380=1/395 9;第二加载循环静活载作用下挠跨比为f2实测/L(fkb-fka)/L=(15.45-5.38)/36 380=1/361 3。因此,实测挠跨比小于设计规定值1.05×(1/2 640)/0.994 2=1/2 500。
4.2 应力结果分析
根据计算结果,节段箱梁在不同荷载作用下梁底理论计算应力值见表4。应力受拉为正,受压为负。
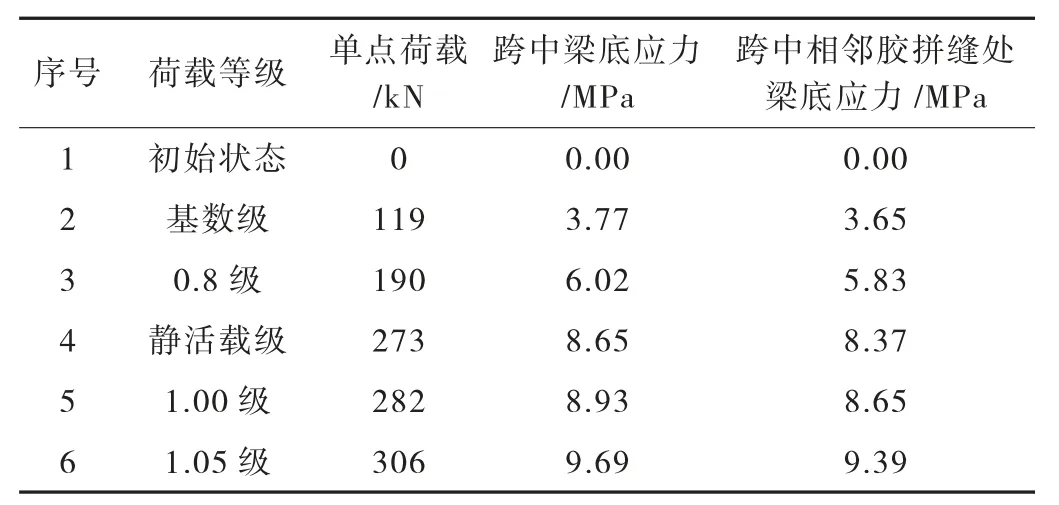
表4 节段箱梁底理论计算应力值
梁底跨中附近共布置25个应力测点,如图6所示,每荷载级加载后测量计算各测点的应力值,梁体混凝土28天抗压强度值为61 MPa,混凝土弹模按36 000 MPa取值,得到梁底各测点的应力值,A侧、C侧梁底各点实测应力值如图10所示。
由图10中的应力值可见,在最大控制荷载(1.05级)作用下,梁底实测最大压应力减小值为7.9 MPa(A6测点),小于理论计算最大压应力减小值9.69 MPa。在各加载等级下实测最大应力值均小于理论计算值,说明梁体刚度比设计值大,除了设计安全度和可靠概率的安全储备外,还在于设计中把结构空间计算的问题转化为平面计算近似求解,所采用的桥梁横向分布系数、边界条件等计算假定会直接影响到箱梁截面应力的大小,使箱梁实际受力小于理论计算值;同时,箱梁混凝土实际强度以及钢筋强度指标均高于设计选用指标,使箱梁结构设计偏于安全。
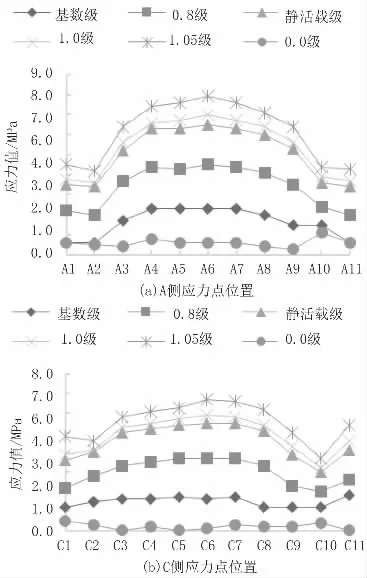
图10 梁底两侧测点实测应力值(单位:MP a)
4.3 裂纹测试结果
试验前用放大镜在梁体跨中两侧下缘和梁底面进行外观检查,采用放大镜在梁体跨中两侧共8~12 m区段下翼缘及梁底面查找裂纹,均未发现裂纹;试验最大控制荷载为1.05级,试验过程中,在各级荷载下查找裂纹,在梁体底面和底部倒角或圆弧过渡段均未发现受力裂缝,表明梁体抗裂性能满足设计要求。
5 结论
通过箱梁静载试验及理论计算分析,得到以下结论。
(1)梁体在最大控制荷载作用下,持荷20 min,梁体底面和底部倒角或圆弧过渡段均未发现受力裂缝,说明节段胶拼对梁体抗裂性影响不大,节段胶拼位置不会成为结构裂缝发展位置。
(2)在第二循环静活载作用下的挠跨比为1/3 613,小于设计规定值1/2 500;在第二循环静活载与基数级作用下的挠度差为10.07 mm,小于理论计算值13.3 mm,说明节段胶拼梁虽然对梁体刚度有一定影响,但具体折减系数尚需进一步研究。
(3)在最大控制荷载作用下,梁底实测最大压应力减小值为7.9 MPa,小于理论计算最大压应力减小值9.69 MPa,且残余应力较小,说明箱梁混凝土实际强度以及钢筋强度均高于设计选用指标,箱梁结构设计具有一定的安全度。
本节段梁在试验荷载作用下,跨中挠度、应力等试验指标均与设计期望值相符,可满足桥梁在设计荷载下的正常使用要求,通过静载试验检验了节段梁结构设计理论和计算模型的准确性,验证了施工工艺的可靠性,为节段预制胶拼箱梁设计与施工提供借鉴。
