起伏天然气掺氢管道气体静置分层过程数值研究
2023-01-26朱红钧陈俊文粟华忠唐堂何山
朱红钧 ,陈俊文,粟华忠,唐堂,何山
1.油气藏地质及开发工程国家重点实验室·西南石油大学,四川成都610500
2.中国石油工程建设有限公司西南分公司,四川成都610041
3.伊尔姆环境资源管理咨询(上海)有限公司,上海虹口200080
引言
氢能的开发利用被认为是绿色低碳转型的重要途径之一,面对石油对外依存度居高不下、能源结构高碳化的客观形势,中国的氢能发展需求尤为迫切[1-5]。利用已有天然气管网进行掺氢输送,是大规模、低成本转运氢能的有效途径[6-11]。然而,天然气管道在设计时并未考虑掺氢输送的潜在需求,在正常输运过程中,管内气体流动绝大多数为湍流,天然气与氢气在较大的湍动强度条件下得以不断掺混,不易出现分层现象,但在管道停输检修时,因密度差的存在,氢气易从天然气中分离出来而出现分层现象,若聚集于管顶的氢气浓度过高,则增加了管道氢致开裂的风险[12-16]。明晰停输后气体静置分层过程、浓度时空演变规律、稳定分层所需时长是决定掺氢输送停输检修窗口期的关键,目前国内外罕见这方面的研究报道。
关于氢气掺入天然气的混合过程,已有学者进行了实验和数值模拟研究。Marangon 等[17]实验测试了氢气-甲烷混合物自充满氧气的密闭箱体底部注入后的扩散过程,在停注0.78 h 后,箱体顶部与底部的氢气-甲烷混合物浓度相差8%,表明气体混合静置后有分层倾向。任少云[18-19]在向充满空气密闭罐体注氢扩散的模拟中也证实了这一趋势。Elaoud 等[20]建立了可压缩氢气-天然气混合物的流动控制方程,采用Hardy-cross 算法进行数值离散,分析了不同氢气浓度对管内压力的影响,指出氢气-天然气混合物的瞬态压力较纯天然气高。闫文灿等[21]以川气东送普光首站为例,采用CFD 软件模拟了不同组分天然气的掺氢混合过程,发现达到均匀掺混的位置与组分浓度密切相关。陈俊文等[22]对混氢天然气管道的分层现象进行了初步探究,模拟证实了氢气会在地势较高的管段聚集,但其研究的管道高差仅为10 m。更大落差的起伏管道内混合气体浓度的时空演化过程,以及浓度超限的临界时距与起伏高差的变化规律亟待明确。
为此,针对起伏掺氢天然气管道静置时气体分层进行了模拟,剖析了地势落差、掺氢比的影响规律,以期为山区(西部)天然气管道掺氢输送,特别是为停输检修安全窗口期的确定提供理论支撑。
1 数值模拟方法
1.1 控制方程
考虑气体的可压缩性,采用非定常雷诺时均纳维-斯托克斯(RANS)方程求解起伏管道内的混合气体分层过程[23]

利用Boussinesq 涡黏法建立雷诺应力与平均速度梯度的关系[24]

式中:

采用标准的k−ε 双方程湍流模型,使方程组封闭[25]

1.2 问题描述及网格划分
本文模拟的起伏管道模型如图1 所示,管径0.5 m,上、下游水平管长5 m,顶部水平跨长10 m,上倾、下倾管与水平面的夹角均为45◦,取10、30、50 和100 m 等4 个高差进行起伏落差敏感性分析。因而,整个管道计算域的体积与起伏高差的关系为

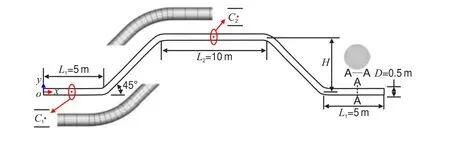
图1 起伏管模型Fig.1 Schematic diagram of the undulating pipeline
初始时刻管内压力8 MPa,温度300 K。模拟选用纯甲烷代替天然气,因为甲烷是天然气中密度较轻的组分,若氢气可以从纯甲烷中分离聚集,那么有其他重组分存在时分层现象必然更为突出。模拟采用的甲烷与氢气物性参数见表1,假设甲烷与氢气均匀掺混,选取3%、5%、10%等3 个氢气初始体积分数进行敏感性分析。在入口和顶部水平管跨中各设置1 个监测点(C1和C2),以监测氢气体积分数随时间的变化历程。计算过程中,不考虑与外界的传热,管壁为绝热壁面边界。

表1 模拟用气体介质的物性参数Tab.1 Physical parameters of the considered gas
对图1 所示的几何模型采用结构化网格划分,并对管道壁面附近网格及弯头网格进行局部加密,第一层网格高度为0.002D,Y=30。通过改变径向及轴向网格单元数,进行网格无关性测试,表2 所示为26×104s 时监测点的氢气体积分数对比结果。

表2 网格无关性验证Tab.2 Mesh independence check
由表2 可见,选择Mesh-2 的网格分辨率(网格总数398 532)已达到预期的计算精度,其横截面及弯头处的网格如图1 所示,故选用该网格分辨率进行数值计算。
1.3 数值算法验证
鉴于目前尚无氢气与甲烷混合气体的静置分层实验研究报道,选用向充满空气的密闭罐体注甲烷扩散的实验报道进行模拟验证[18],验证采用的模拟参数与实验参数完全一致,模拟结果见图2。

图2 稳定后罐内甲烷体积分数分布Fig.2 Distribute of methane volume fraction at different positions in the tank after stabilization
由图2 可见,实验测点的甲烷体积分数与模拟结果吻合较好,证明本方法可以有效模拟不同气体的混合扩散与静置分层过程。
2 数值模拟结果与分析
2.1 气体分层现象
图3 为高差10 m 的起伏管内初始氢气体积分数为3%的混合气体在1 000 s 时的流线图,此时管内有明显的流动现象,底部水平管内流线聚集于下部,且近似平行,速度小于0.04 m/s;倾斜管内流线缠绕交织,但可以辨识出回旋的大涡结构,表明存在上行和下行气流的剪切作用,且最大流速出现在壁面附近,达到0.10 m/s;顶部水平管内流线聚集于上部,也近似平行,但在跨中处有明显扰动,说明两侧气体在该处汇聚;因流动的转向,弯头处的流线较为杂乱,且下部弯头更为明显。

图3 起伏管内瞬时流线图(1 000 s)Fig.3 Instantaneous streamlines in the undulating pipeline(1 000 s)
为进一步分析倾斜管内气体的流动历程,截取高度为4~6 m 的倾斜管段,展示典型时刻该处的氢气体积分数分布与速度分布,如图4 所示。

图4 上倾段内不同时刻的氢气体积分数与速度分布Fig.4 Distribution of hydrogen volume fraction and associated velocity at representative moments in the upwardly inclined pipe segment
在100 s 在400 s 在1 000 s 在1.11 h 图5 为起伏管不同时刻的氢气体积分数云图。 图5 起伏管不同时刻的氢气体积分数云图Fig.5 Contours of hydrogen volume fraction at different moments in the undulating pipeline 由图5 可见,氢气逐渐在顶部水平管的上部聚集,且横截面上的垂向体积分数逐渐增大,在t=55.56 h 时,最大体积分数达到3.76%;与之相反,底部水平管的下部氢气体积分数逐渐减小,在t=55.56 h 时,最低体积分数降至2.36%。在达到稳定分层时,只存在垂向体积分数梯度,沿水平管管轴方向体积分数达到均匀分布。 图6 为入口及顶部水平管跨中监测点氢气体积分数随时间的变化曲线,t<1 000 s 时,监测点的氢气体积分数随时间变化波动明显,体现了管内气体剪切作用产生的影响。t≥1 000 s 时,随管内气体速度的减小与剪切作用的减弱,监测点氢气体积分数增长速度逐渐减缓,在t=55.56 h 时趋于平稳。 图6 不同位置监测点氢气体积分数随时间的变化情况Fig.6 Variation of the hydrogen volume fraction over time at different monitoring points 图7 为不同起伏高差时顶部水平管跨中监测点C2的氢气体积分数增长率随时间的变化曲线。 图7 不同起伏高差时监测点C2 的氢气体积分数增长率随时间的变化情况Fig.7 Variations of the hydrogen volume fraction growth at the monitoring point C2 over time at different undulating heights 在t≤100 s 时,该监测点未捕捉到氢气体积分数的变化,但不代表该时间段内管道垂向氢气体积分数没有变化(图4)。在100 s 在t>400 s 时,因气流剪切作用的减弱,氢气体积分数增长率明显减小,尽管仍有小幅波动,但不同高差的曲线之间没有明显区别。 图8 呈现了不同起伏高差管内气体最大流速随时间的变化历程,可见,气体流速经历了先增大后减少并逐渐趋于稳定的过程。 图8 不同起伏高差管内气体最大流速随时间的变化曲线Fig.8 Variation curve of the maximum gas velocity over time at different undulating heights 当高差超过30 m 时,气流达到最大流速所需的时间仅为高差10 m 时的一半,且高差越大,最大流速越大。高差100 m 时的最大流速为1.45 m/s,约为高差10 m 时的6.57 倍。此外,当高差超过30 m时,气流最大速度的波动历程耗时较短,表明起伏高差的增大加速了剪切过程。相应的,管内气体最大剪切应力与最大流速的变化历程一致,见图9,说明起伏高差的增大同时加剧了气体的剪切作用。但由于起伏高差越大,管内气体垂向流动的空间越大,在t=55.56 h 时,大起伏管内的气体最大流速与最大剪切应力仍大于小起伏管对应的数值。 图9 不同起伏高差管内气体最大剪切应力随时间的变化曲线Fig.9 Variation curve of the maximum shear stress over time at different undulating heights 不同初始氢气体积分数的起伏管内气体达到稳定分层后,最大氢气体积分数随起伏管高差或总容积的增加而增长,但增长率有一定的波动,见图10。 由图10 可见,初始氢气体积分数为5%和10%时,起伏高差从50 m 增至100 m 的最大氢气体积分数增长率有一定程度的下降,而初始氢气体积分数为3%时呈现相反变化趋势。此外,起伏高差或管道容积越大,气体达到稳定分层所需的时间越长,但不同初始氢气体积分数的稳定分层所需时间增长率不同,初始氢气体积分数为3%和5%时,高差30 m 起伏管出现最大的时间增长率,而初始氢气体积分数为10%时,高差50 m 起伏管出现最大的时间增长率,见图11。 图10 最大氢气体积分数增长率随起伏高差和容积的变化Fig.10 Variation of the maximum hydrogen volume fraction growth with the undulating height and total volume 图11 稳定分层所需时间增长率随高差和容积的变化Fig.11 The required time of stabilized stratification varying with the undulating height and total volume (1)静置管内气体流动经历了4 个阶段:剪切启动与增强阶段,管壁出现近似线性分布的逆增长速度梯度;剪切起旋与衰减阶段,线性速度剖面演变为对数分布,最大流速逐渐减小;旋涡消亡与流动平整阶段,最大速度进一步减小,速度剖面恢复至线性分布;流动减速与垂向分层阶段,管内气体流速整体下降,最终减小至0。 (2)起伏高差越大,管道总长度越长,管内容积也越大,氢气达到稳定分层后聚集于顶部水平管的体积分数越高,达到稳定分层所需的时间也越长。在管长和高差同时增长的条件下,初始氢气体积分数越高,稳定分层后的氢气体积分数增长越大,但稳定分层所需时间缩短。因此,实际天然气管道掺氢输送过程中,需注意气体分层带来的局部氢气体积分数过高的影响,明确增至风险体积分数的时间窗口,避免引发安全事故。本文计算结果为掺氢天然气管道停输后的静置安全时长及检修期安全窗口的确定提供了依据。

2.2 起伏高差的影响





3 结论
