基于尾流振子模型的套管涡激振动响应研究

2023-01-26赵翔谭明

西南石油大学学报(自然科学版) 2022年6期

赵翔，谭明

西南石油大学土木工程与测绘学院，四川成都610500

引言

PIP（Pipe In Pipe）系统（套管）作为一种海洋立管，主要连接海洋悬浮平台和海底井口，为海洋油气资源的开采输送提供便利。因其具有较好的减振效果，近年来得到了广泛的应用。PIP 系统通常是由外部管道、内部管道以及中间连接层3 部分构成[1]。

目前，有许多研究者通过分析或实验的方式研究了套管的静态特性和动力学问题。Alrsai 等[2]研究了套管的屈曲行为，并提出了每种模式的经验表达式；Li 等[3]开发了一种非线性有限元方法以用于确定内管和外管的碰撞位置；Doan 等[4]利用了有限差分法和尾流振子模型法对柔性立管的涡激振动问题进行了研究，提出了一种可以提供高效和稳定计算的数值模拟方法；Bi 等[5]利用了套管的特殊结构布局，设计了非常规结构TMD 系统，将优化后的弹簧和减震器安装在内外管道之间的环形空间，能够在不增加任何附加质量的情况下显著地降低内部管道的振动；Li[6]提出了一种适用于套管的非线性有限元方法，即一种新的内外管道碰撞屈曲分析算法；Wang 等[7]发现采用超轻质水泥复合材料填充系统表现出了非常好的冲击性能，并且可以有效限制局部压痕的扩展；Orynyak 等[8]提出了一种用能量法来确定海洋立管受到输送流体作用的强迫振动的频率，并通过实例证实了方法的有效性；Shahali 等[9]以欧拉-伯努利理论为基础，研究了均匀外流作用下黏弹性输流管道的非线性动力响应。研究中发现，当发生锁定现象时，内部流体速度和黏弹性阻尼对管道的振幅和锁定区域范围有重要影响；Mitsuishi等[10]考虑催化转化器中的传热增强作用，在数值模拟中发现，双涡流在增强传热方面起主导作用。

套管在受到海洋流体作用时，会在其两侧产生交替脱落的旋涡，从而引起套管发生周期性的振动，即涡激振动。当套管的振动频率接近其固有频率时，便会发生共振，产生较大振幅的涡激振动响应，从而导致结构发生损伤，降低其工作安全性。现有的涡激振动研究方法通常分为实验法[11-13]、计算流体动力学方法以及经验模型法[14-17]。实验方法具有数据可靠、现象明显易观察等优点，但其研究成本较高，并不适用于所有研究；在现有水平下，CFD方法对于模拟这种大尺寸的模型是比较困难的；经验模型法也有广泛的应用，其中，基于加速度模型来描述立管尾部流场的尾流振子模型受到国内外许多研究者的认可[18]。

本文对海洋立管的研究以横向振动为主，基于Euler-Bernoulli 双梁理论建立了套管结构振动模型，结合尾流振子模型，建立了套管在海洋流体作用下的PIP 流固耦合振动模型，并利用谐波平衡法进行求解，得到了该耦合模型中套管涡激振动的位移响应解析表达式。通过与现有研究结果进行对比，验证了本文计算模型的正确性，并分析了不同无因次波数、直径比、连接层刚度以及张力对套管响应特性的影响规律。

1 模型分析

1.1 套管系统的振动模型

图1 给出了套管系统示意图。套管通常具有很高的细长比[19-21]，从而采用Euler-Bernoulli 双梁模型，并且将中间链接层视为线性弹簧，见图2。

图1 套管系统示意图Fig.1 Schematic diagram of casing system

图2 双梁系统Fig.2 Double-beam system

计算中忽略了海洋立管的阻尼和中间连接层的阻尼与质量，考虑涡激振动下海洋立管的动力学响应，建立套管的振动方程[22-23]

1.2 尾流振子模型

采用改进的Van der pol 方程来描述套管系统尾迹的动力学问题[24-27]，其表达式为

1.3 套管和尾流振子耦合

为了方便后面计算以及分析，引入一些无因次参数

将式（7）代入式（1）、式（2）和式（6）中，得到无因次方程组

为了分析上述流固耦合问题，采用谐波平衡法进行计算，假设式（8）的解为

计算时，根据式（10）先求出ω 的值，结合式（11）就可计算出套管内、外管道的振动位移。

1.4 数值模型验证

验证过程中选取了文献[24]中的参数进行对比分析，设置中间连接层刚度为零，从而可以将本文模型退化成单管道模型，可以与文献中的剪切流实验数据进行对比验证，见图3。

计算的主要相关参数为：斯特劳哈尔数St=0.2；细长比L/D=781；质量比µ=1.75；外部管道的无因次刚度a1=0；中间连接层的刚度k=0。从图3 中可以看出，本文计算结果和文献的计算结果吻合度较好，从而验证了本文模型的正确性。

图3 计算外部管道位移与文献结果对比Fig.3 Displacement of outer pipes compared with the results of references

2 分析与讨论

分析中，为了方便分析，在没有说明的情况下，一些重要参数取值为：细长比L/D=781；外、内部管道的弹性模量相等（E1=E2）；质量比µ=1.785；内部管道的直径与海洋立管的直径比d/D=0.8；外部管道的无因次张力c1=4.0；内部管道的无因次张力c2=3.2；外部管道无因次刚度a1=1 000；与外部管道质量相关的无因次连接层刚度a2=10；内部管道无因次刚度b1=640；与内部管道质量相关的无因次连接层刚度b2=6.4。

2.1 无因次波数的影响

无因次波数n与无因次波数系数m成正比，因此，以m的变化关系来确定无因次波数n和套管频率比的关系图，如图4 所示。图4 中，计算使用的无因次管道刚度和与外部管道质量相关的无因次连接层刚度均取2。

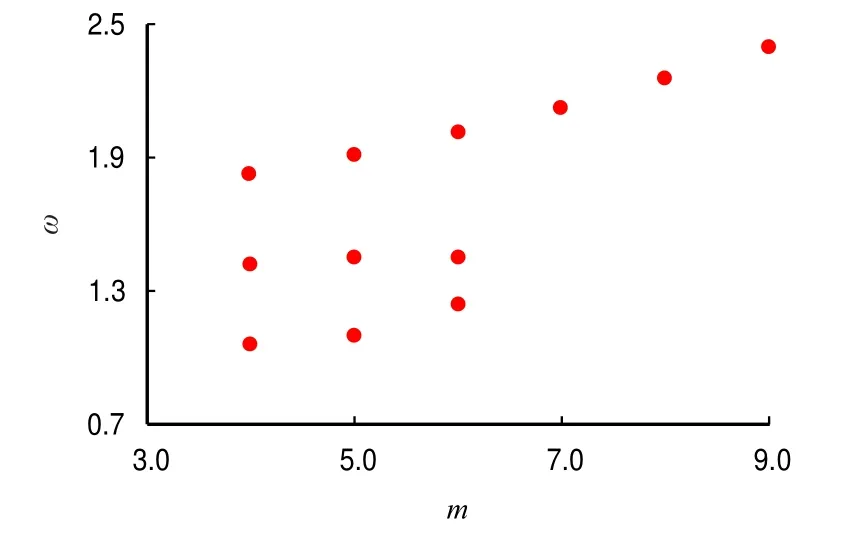
图4 不同m 的频率比Fig.4 Frequency ratio under the action of different dimensionless wave numbers coefficient

从图4 中可以看出，m不超过6.0 时，套管在同一条件下存在多个频率，即存在多频共存的情况，从而导致套管的振动不稳定；当m大于6.0 时，套管的频率出现唯一值，此时套管的振动表现为单一振动形态。

图5 中展示了在不同m时升力振子的幅值q0变化情况。

图5 不同m 的升力振子幅值Fig.5 Amplitude of lift oscillator under the action of different dimensionless wave numbers coefficient

当m在不超过6.0 时，即低频区域，随着m的增大，无因次波数增大，升力振子的幅值q0呈现先增大后减小的趋势；当m大于6.0 时，即高频区域，随着无因次波数系数的增大，升力振子的幅值q0呈现逐渐减小趋势。

图6 展示了在不同m作用下套管位移幅值变化情况。

从图6 中可以看出，m的变化对内、外管道的影响趋势基本一致。在低频区域，随着无因次波数系数的增大，管道位移幅值的绝对值呈现先增大后减小的趋势；在高频区域，随着无因次波数系数的增大，管道位移幅值的绝对值呈现逐渐减小的趋势。

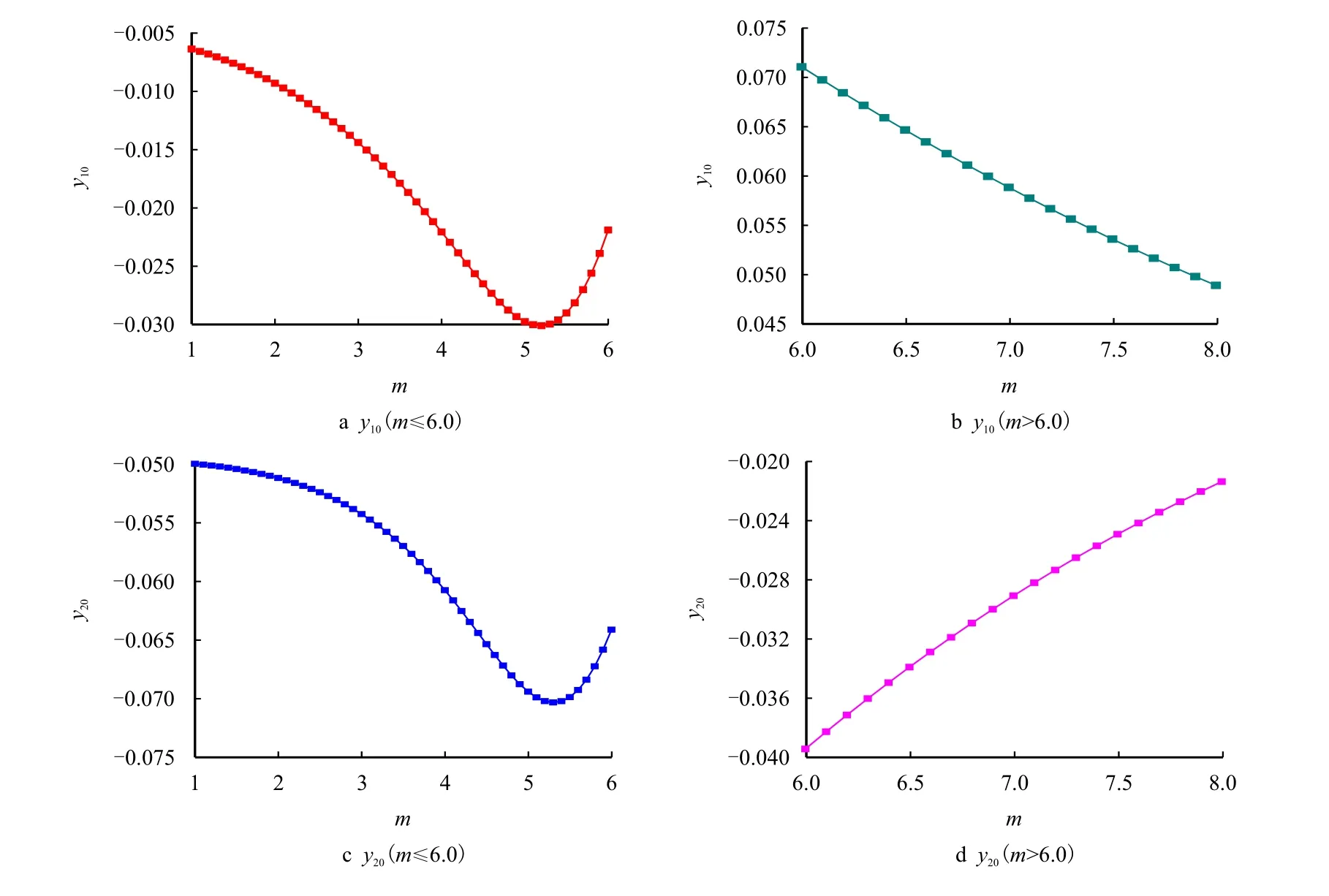
图6 不同m 作用下的套管位移幅值Fig.6 Amplitude of PIP displacement under the action of different dimensionless wave numbers coefficient

2.2 直径比的影响

分析时，无因次管道刚度和无因次连接层刚度取2，外部管道和内部管道无因次张力均取43.1，其余参数与验证部分相同。这里选取的直径比分别为0.650、0.675、0.700、0.750、0.800 和0.850，研究直径比对外管道和内管道的影响（图7，图8）。

图7 外部管道在不同直径比下的响应Fig.7 Response of outer pipes at different diameter ratios

由直径比对外部管道响应图（图7）可见，当外部管道的振动模态不同时，内外管道的直径比对其相应的影响规律不尽相同。当振动为一阶模态时，随着内外管道直径比的增大，外部管道的响应呈现先减小后增大的趋势，在直径比0.700 时出现最小值；当振动为二阶模态时，随着内外管道直径比的增大，外部管道的响应呈现逐渐增大的趋势，在直径比0.650 时出现最小值；当振动为三阶模态时，随着内外管道直径比的增大，外部管道的响应呈现先增大后减小的趋势，在直径比0.650 时出现最小值；当振动为四阶模态时，随着内外管道直径比的增大，外部管道的响应呈现逐渐减小的趋势，在直径比0.700～0.850 时产生的变化较小。

图8 给出了不同直径比对内部管道响应的影响关系图。可以看出，当内部管道的振动模态不同时，直径比对其相应的影响规律基本一致。随着直径比的增大，内部管道的响应呈现逐渐减小的趋势，减小的趋势不随着模态的改变发生改变。

图8 内部管道在不同直径比下的响应Fig.8 Response of inner pipes at different diameter ratios

图9 分别展示了套管外部管道、内部管道在不同直径比下响应的变化情况。

图9 套管在不同直径比下的响应Fig.9 Response of PIP at different diameter ratios

由图9 可见，随着直径比的增大，外部管道的振动幅值先增大后迅速减小，接着小幅度增加，逐渐趋于稳定的趋势。当直径比0.750 时，产生最小的外部管道振动位移幅值。随着直径比的增大，内部管道的振动幅值呈现先增大后减小的趋势。此外，当直径比大于0.750 时，直径比的变化对内部管道的位移幅值影响减弱。因此，在相同件下，直径比为0.750 左右的套管具有较好的抗振性能。

2.3 连接层刚度的影响

图10 给出了不同无因次连接层刚度作用下外部管道的振动均方根位移，其余参数均与上述相同，直径比取0.800，分析了无因次连接层刚度取5、10、15、20、25 和30 时外部管道的变化情况。由图10 可以发现，外部管道的振动均方根位移的变化规律具有一致性，随着无因次连接层刚度的增大，外部管道在每个振动模态下的位移均呈现增大的趋势，并且逐渐趋于稳定。

图10 外部管道在不同无因次连接层刚度下的位移Fig.10 Displacement of outer pipes at different dimensionless connection layer stiffnesses

相比于外部管道的位移变化，内部管道受到无因次连接层刚度的影响相对较小，产生的位移变化不大，如图11 所示。

图11 内部管道在不同无因次连接层刚度下的位移Fig.11 Displacement of inner pipes at different dimensionless connection layer stiffness

从图11 可以看出，随着无因次连接层刚度的增大，内部管道的位移呈现增大的趋势，增幅较小。可以推断，当振动模态大于等于三阶时，无因次连接层刚度对内部管道的位移影响更小。

图12 给出了内、外管道在七阶模态下随无因次连接层刚度变化的均方根位移变化图，即在高频区域的变化情况。随着无因次连接层刚度的增大，外部管道的位移呈现先减小后增大的趋势，并且逐渐趋于稳定，在无因次连接层刚度取10 时，外部管道的振动位移幅值最小（图12a）；而内部管道变化趋势与外部管道的变化趋势基本一致，但变化幅度存在一定差异（图12b）。

图12 套管在不同无因次连接层刚度下的位移Fig.12 Displacement of PIP at different dimensionless connection layer stiffness

2.4 张力的影响

内外管道的无因次张力存在一定差距，为方便处理，假设施加在外部管道和内部管道上的无因次张力相同，分析张力对外部和内部管道响应的影响。图13 为考虑了无因次张力取33.1、38.1、43.1、48.1 和53.1 时的外部管道无因次位移。

图13 外部管道在不同无因次张力下的位移Fig.13 Displacement of outer pipes under different dimensionless tensions

从图13 可以看出，随着无因次张力的增大，外部管道的位移呈现增大的趋势，不随模态的改变而发生变化。

图14 中展示了内部管道在不同无因次张力作用下的位移。不难发现，随着无因次张力的增大，内部管道的位移呈现逐渐增大的趋势，但变化的幅度较小。此外，随着模态的增加，张力对内部管道位移的影响逐渐增大，变化幅度逐渐增大。

图14 内部管道在不同无因次张力下的位移Fig.14 Displacement of inner pipes under different dimensionless tensions

图15 给出了套管在高阶模态下的均方根位移变化图。

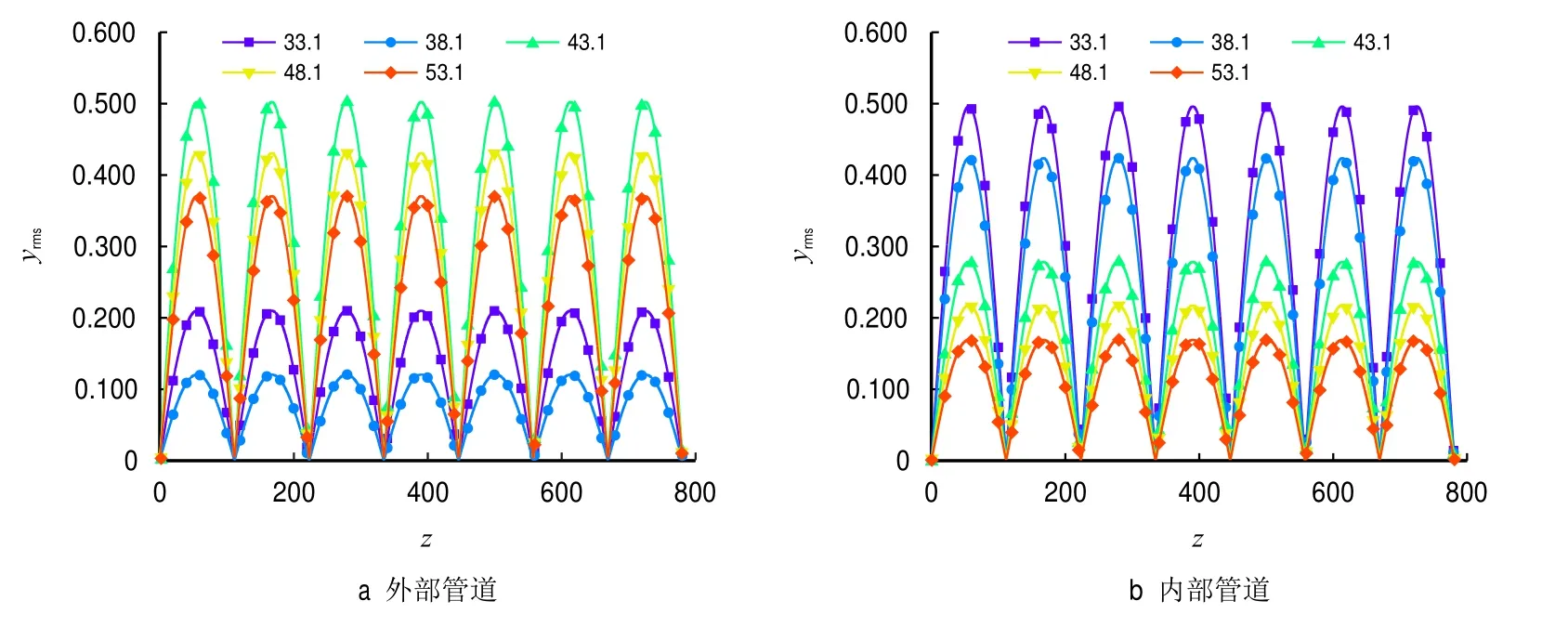
图15 套管在不同无因次张力下的位移Fig.15 Displacement of PIP under different dimensionless tensions

图15a 展示了外部管道的均方根位移变化情况，从图中可以看出，当无因次张力在33.1～38.1时，外部管道的位移呈现减小的趋势；当无因次张力在38.1～43.1 时，呈现增大的趋势；当无因次张力大于43.1 时，外部管道位移呈现减小的趋势；图15b展示了内部管道的均方根位移变化情况，从图中可以看出，随着无因次张力的增大，内部管道的位移呈现逐渐减小的趋势。

图16 中给出了在不同无因次张力作用下套管各阶模态的频率比变化情况。从图中可以看出，当模态小于3 时，随着无因次张力的不断增大，频率比呈现减小的趋势，从而导致套管的各个管道位移减小，但影响相对较小。当模态大于3 时，无因次张力对频率的影响逐渐增大。在三阶模态下，随着无因次张力的增大，频率比呈现先减小后增大的趋势；在四阶模态下，随着无因次张力的增大，频率比呈现逐渐增大的趋势，套管的涡激振动常表现出高阶模态振动以及多模态共存的状态，因此，张力对套管中内、外管道的振动具有较明显的影响，在工程中产生的影响不能忽视。。