基于同步电机等效电路的分布式可再生能源发电虚拟同步机控制

王 蔚，侯士亮，刘玉建，刘太东，邹方朔

（国网山东省电力公司超高压公司，山东 济南 250118）

0 引言

为提高发电的经济性和环保性，越来越多的新能源发电设备接入电网之中。2019年中国新能源装机容量已突破4 亿kW，占总发电容量的20.6%，新增装机容量5 610 万kW，占到新增装机容量的58%。新能源中，分布式光伏装机突破6 000万kW，成为重要的发电手段［1］。

新能源发电大多通过变流器或逆变器接入电网，由于电力电子装置的运行特性与传统的水火电机组差异较大，因此新能源容量占比高的地区往往面临频率问题和电压问题，故障工况下尤甚。针对频率问题，已有文献提出了虚拟同步电机控制策略，通过模拟同步电机的运行特性缓解新能源接入的频率问题。文献［2-7］最早提出了虚拟同步发电机的概念和模型，通过模拟同步发电机的转子摇摆方程，使得逆变器具有同步发电机的惯性运行特性，以此来缓解各种功率扰动带来的频率问题。文献［8-9］提出了自适应虚拟同步发电机控制的概念，通过各种自适应算法自动调整虚拟同步机的虚拟惯量常数和阻尼系数等参数，从而获得最佳的频率响应效果。上述研究针对逆变器接入电网产生的频率问题，已经取得了可观的进展。然而，对于故障工况下的电压问题，基于新能源发电的虚拟同步机相关研究却甚少涉及。

在目前的实际电网当中，针对故障情况下的无功和电压问题，工程上还采用配置同步调相机等方式来解决［10-15］。这是因为，相比静止无功补偿器等传统的电力电子无功补偿设备，新一代调相机在严重故障下，尤其是三相严重故障下有着更好的表现，能将电压更快速地拉回到额定值［16］。而这一现象的成因是由于同步调相机具备次暂态效应，可以增强故障工况下的电压支撑能力［15-19］。例如，在中国酒泉—湖南送端电网和华东受端电网中，新一代调相机有着较为广泛的应用，仿真结果和工程实际表明调相机对于电压稳定有较好作用［10］。而在光伏等新能源大规模接入的地区，调相机对于提升电压稳定性也有较好效果。在中国的西北地区有大量光伏和风电等新能源接入，并有750 kV 的长距离输电线路，对该算例进行的仿真研究表明调相机对于提升该地区的电压稳定性有着最佳的效果［11］。文献［12］的研究表明，在新能源大规模接入的地区当中，相比在与输电线路连接的母线场站处集中配置多台大容量调相机而言，在各个新能源场站分布式配置几十至数百兆乏容量的小型调相机能够更好地解决暂态工况下的电压稳定问题，且在经济性上更好。但采用调相机制造工艺复杂、维护费用高、噪音大，将调相机分散地布置在较为空旷的新能源发电区域将带来更高的运输和维护成本，且这种配置方式也没有充分发挥逆变器的调节能力。

针对以上问题，提出一种基于同步发电机等效电路模型的新型虚拟调相机控制策略。该策略主要针对夜间具有充足无功调节能力的光伏逆变器，可以在新能源大规模接入的区域给逆变器赋予类似于调相机的次暂态无功响应特性和惯性，以增强区域的暂态无功支撑能力和暂态电压稳定。

1 同步发电机的建模

调相机本质上仍然是一台有功出力为零的同步电机，因此虚拟调相机控制本质上是通过建立同步发电机的模型，将逆变器模拟为同步发电机。目前已有研究提出的将逆变器模拟为同步发电机的控制方法，大多是基于简化的三相对称圆形转子的同步机模型，而忽略了同步发电机的d轴和q轴效应，这将导致逆变器无法具有次暂态特性，因而无法在发生故障时通过瞬间发出无功来保证电压稳定。因此，本文采用同步发电机的完整模型，以使得逆变器具有同步发电机的次暂态效应。

1.1 同步发电机的等效电路方程和机械方程

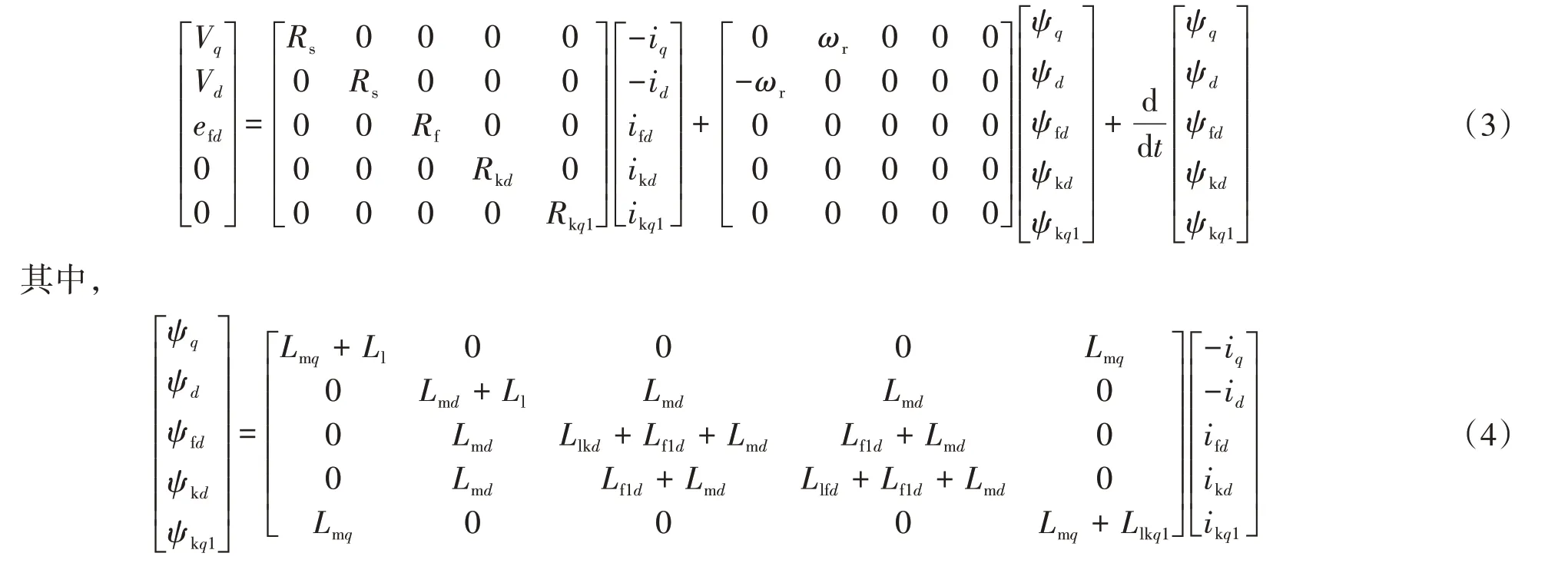
为模拟同步发电机的次暂态效应，须先对同步发电机的等效电路进行详细的建模。由文献［20-21］可知，同步发电机（隐极式）的dq轴等效电路可由图1 表示，等效电路图对应的电气方程如式（1）所示。该模型需要6 个变量来表示同步发电机的运行状态，即电枢电流id和iq，励磁支路电流ifd，d轴阻尼绕组电流ikd，以及q轴阻尼绕组电流ikq1和ikq2。Rs，Ll，Lmd和Lmq分别为定子电阻，定子漏感，d轴、q轴定子电感；Llkd和Rkd为d轴阻尼绕组电感和电阻；Llfd和Rfd为励磁绕组电感和电阻；efd为励磁绕组电动势；Llkq1，Llkq2，Rkq1，Rkq2为q轴阻尼绕组电感与电阻；Lf1d称为Canay电感。

图1 同步发电机的dq轴等效电路模型

式中：ψq为q轴磁链；ψd为d轴磁链；ψfd为励磁支路磁链；ψkd为d轴阻尼绕组磁链；ψkq1、ψkq2为q轴阻尼绕组磁链。

若为凸极机，则q轴等效电路中的最右侧q2部分会消失，q2部分为图1（b）中红色虚线框标注部分。凸极机需要5 个变量来表示等效电路方程，则在相应的矩阵和变量向量中删去q2有关的行和列即可，即：

同步发电机的机械模型如图2 所示，其中，Tm为原动机输入转矩；Te为电磁转矩；H为惯性常数；Kd为阻尼系数；ωn为额定角速度；θ和ω分别为发电机的角度和转速；s为拉普拉斯变换算符。其机械方程为

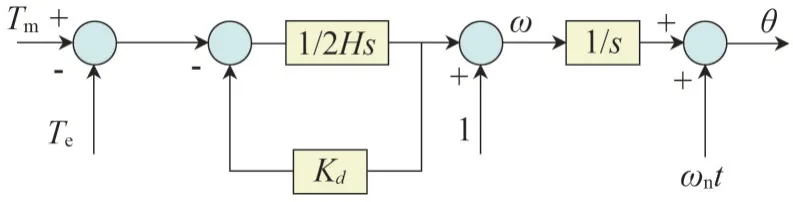
图2 同步电机的机械模型

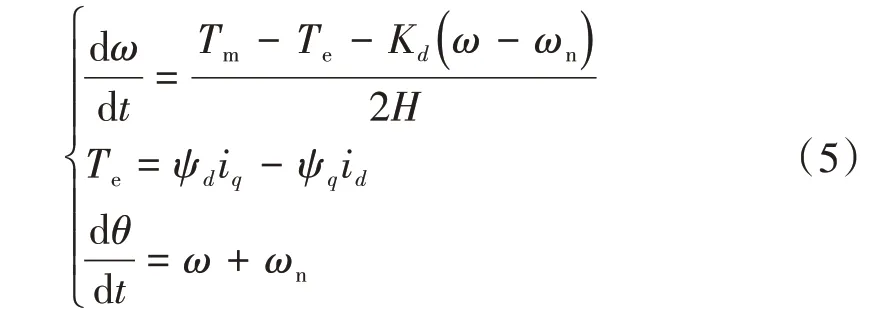
较大的惯量意味着较好的频率支撑，较大的阻尼意味着对扰动后的振荡具有较大的削减作用，但太大的数值也可能使得系统失稳。为此，应当参考实际发电机的参数，以使得其惯量和阻尼处于合理的范围内。

1.2 同步发电机的参数转换

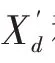
由文献［20］可知，以实验测得运行电抗，d轴短路常数以及q轴开路常数的凸极同步发电机为例，测量得到的参数分别为定子电阻和漏抗Rs和Xl，稳态电抗Xd和Xq，暂态电抗，次暂态电抗和，d轴短路常数以及，以及q轴开路常数。由于是凸极机，所以不具有q轴暂态参数，电抗和电阻单位均为标幺值，时间常数单位为秒。则标准参数和基本参数之间的转换式可按照式（6）—式（19）进行精确地转换。

1）定子参数。

首先计算定子相关的参数为

式中：Rs-fnd为等效电路定子电阻；Rs-std为标准参数定子电阻。

2）d轴阻尼和励磁绕组参数。

为了计算d轴阻尼和励磁绕组的相应参数，需要计算一些中间变量，可以由简单的代数计算得到：

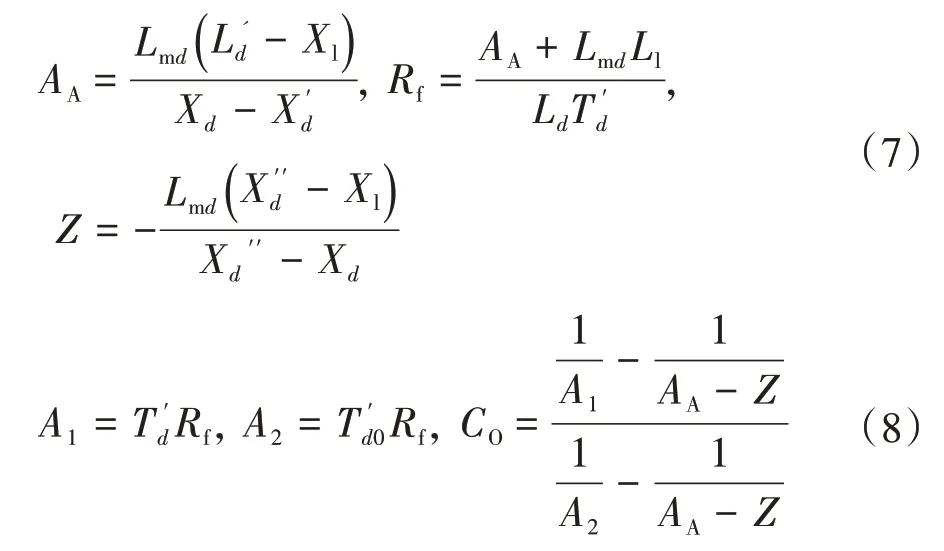
由此可以得到等效的d轴开路常数和q轴短路常数为

再由所有的等效dq轴常数得到以下的中间变量：

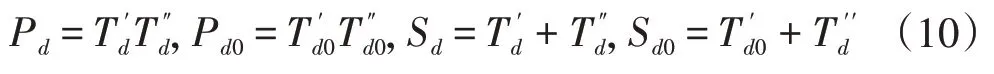
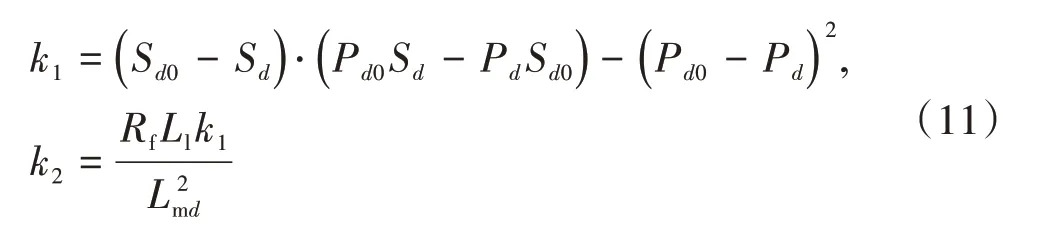
接下来计算较为复杂的中间变量。首先定义三个常数：

设x为Ax2+Bx+C=0 的所有根，则中间变量Tkd为所有根的最大绝对值。得到Tkd后，可以继续计算剩下的中间变量为

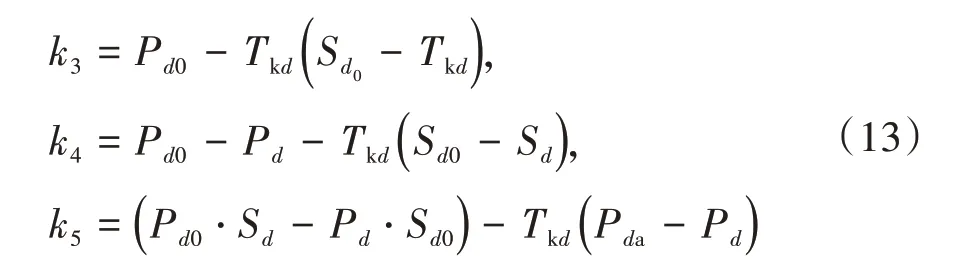
最后可以得到d轴励磁和阻尼绕组的相应参数为

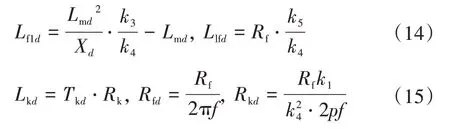
3）q轴阻尼绕组参数。

2 同步发电机的次暂态效应分析

同步发电机的次暂态效应主要取决于其次暂态参数，当同步发电机机端发生三相短路时，主要决定定子短路电流的大小；而当距离机端有一定距离的高感性线路上发生三相短路时，该参数主要决定了三相短路故障瞬间发电机机端电压的幅值和短路电流的大小［22］。下面分析次暂态效应的成因。

由文献［23］可知，当同步电机机端发生三相突然短路时，其a相短路电流瞬时值为

定子a相短路电流的交流分量Iac为

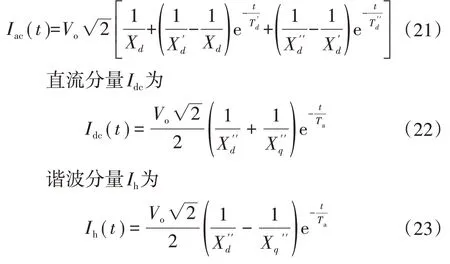
式中：Vo为短路前一瞬间端电压标幺有效值；ω为转速，在短时间的故障过程中，可以近似认为保持恒定；λ为转子角。

3 逆变器的虚拟调相机及无功控制

3.1 适用于虚拟调相机的虚拟励磁控制

和实际同步发电机的励磁控制类似，虚拟励磁控制也是为了控制虚拟调相机的虚拟励磁电压和虚拟励磁电流，以控制逆变器的实际端电压和输出的无功功率。本文的虚拟励磁控制参考了实际励磁控制系统的设计［21-22］，如图3 所示，图3 中Vref为基准电压。为模拟实际励磁系统的特性，图3 包含端电压Transducer、调压器、励磁器、超前—滞后补偿器和阻尼滤波器，这些环节均用一阶系统来模拟，Tr为端电压Transducer常数，Ka和Ta分别为调压器增益和时间常数，Ke和Te为励磁器增益和时间常数，Kf和Tf为阻尼滤波器的微分反馈增益和时间常数。虚拟励磁控制的作用在于调节无功输出，以使得逆变器并网点端电压处于额定值。

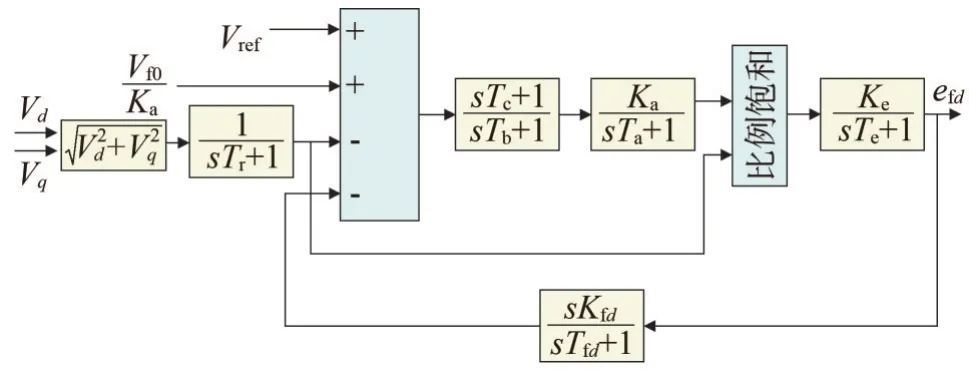
图3 虚拟励磁控制

3.2 逆变器的开关控制

按照上文的控制方式，即可最终应用于逆变器的开关控制。对于实际的逆变器来说，其并网点的电阻和电感可以等效为虚拟调相机的定子电阻和电感，而三个桥臂的中性点电压即可等效为发电机的三相内电势，即：

根据发电机建模方程以及虚拟励磁控制，可以得到最终的逆变器PWM控制策略，如图4所示。

图4 逆变器的虚拟调相机控制

4 案例研究

为了测试所提控制方法的效果，选取一典型的单机—输电线路—无穷大母线案例进行研究。该案例拓扑及参数如图5 所示，逆变器经升压变压器连接至100 km 的传输线路再连接至一无穷大母线，变压器高低压侧各有一有功负荷。在t=10.1 s时，变压器高压侧负荷与传输线之间发生三相接地故障，接地电阻和电感分别为1 mΩ 和1 mH。t=10.2 s 时，故障清除。该案例主要用于研究虚拟调相机控制的次暂态效应对故障期间的电压支撑作用，以及虚拟惯量对于频率的支撑作用。

图5 研究案例的拓扑及参数

虚拟调相机控制的参数如表1 所示，其等效电路模型为凸极机模型，电气参数均为标准参数，时间常数为d轴短路常数和q轴开路常数。除时间常数单位为秒以外，其他所有参数的单位均为标幺值。虚拟励磁控制的参数如表2所示，其中Efmin、Efmax表示虚拟励磁电压的最小值和最大值。

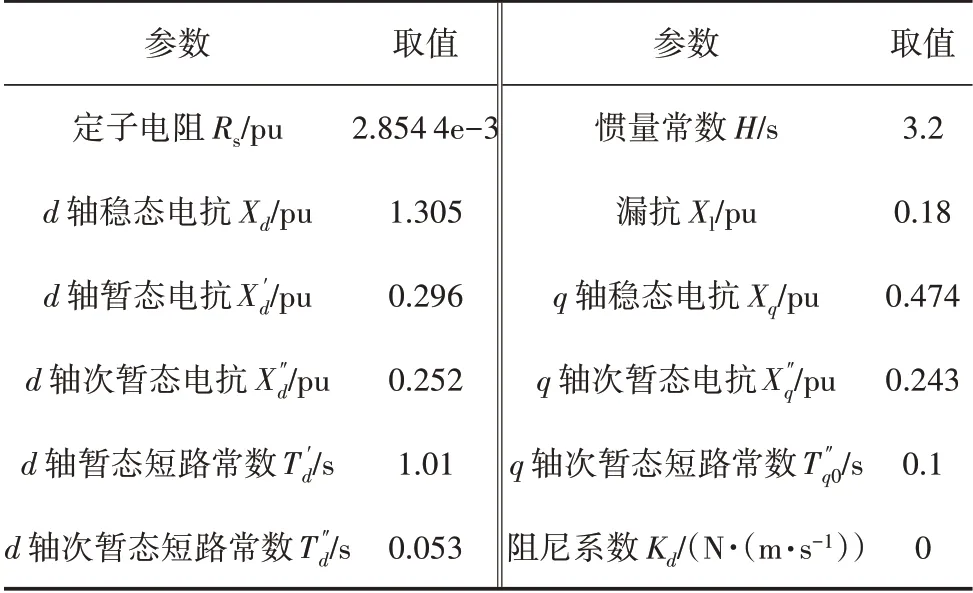
表1 虚拟调相机控制的标准电气参数及机械参数

表2 虚拟励磁控制的参数

4.1 虚拟调相机控制的次暂态效应研究

为研究其次暂态效应对电压的支撑作用，需观察不同次暂态参数下的控制效果。同步电机的次暂态电压效应主要与其次暂态电抗有关，电抗越小，故障期间对电压的支撑效果越明显。现原始的次暂态电抗分别改为0.252、0.2 和0.15，观察三种情况下对应的控制效果。按照参数转换，可以得到三种次暂态电抗参数下等效电路模型的各个参数，如表3—表5所示。

表3 =0.252 时的等效电路参数 单位：pu

表3 =0.252 时的等效电路参数 单位：pu

表4 =0.2 时的等效电路参数 单位：pu

表4 =0.2 时的等效电路参数 单位：pu

表5 =0.15 时的等效电路参数 单位：pu

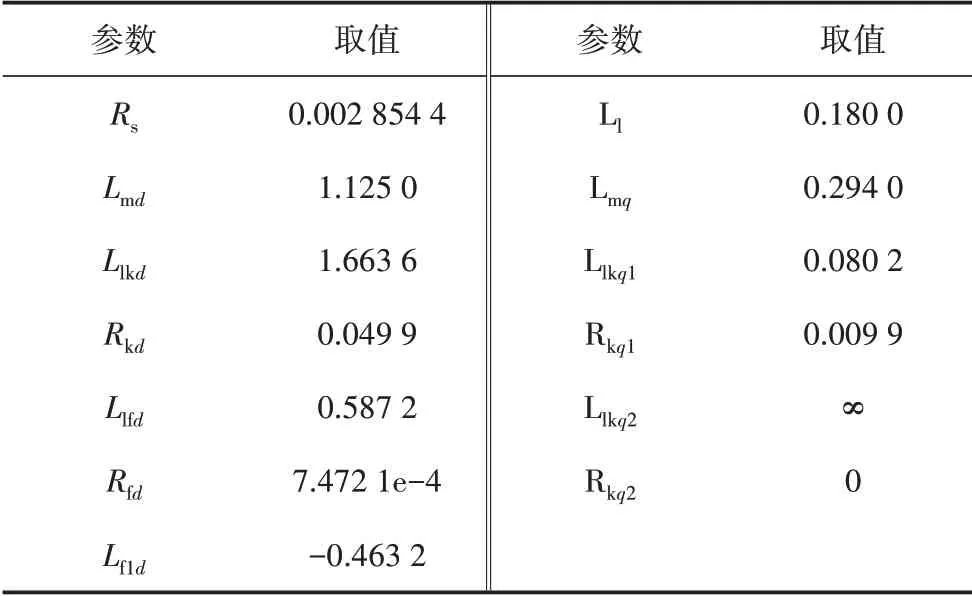
表5 =0.15 时的等效电路参数 单位：pu

在MATLAB/Simulink 软件中搭建图5 的仿真模型。其中，逆变器的建模采用平均模型［24］。三种次暂态电抗参数下的故障期间端电压（变压器低压侧）波形如图6 和图7 所示，可以看出，次暂态电抗对于稳态时的波形几乎没有任何影响，而在故障期间时，次暂态电抗减小会使得电压支撑能力加强，无论是故障瞬间还是故障持续一段时间后。当次暂态电抗为0.252 pu 时，故障瞬间电压幅值会跌至0.38 pu 左右，而当次暂态电抗为0.15 pu 时，故障瞬间的电压保持在0.5 pu 以上，故障瞬间的支撑效果大幅提升，并且在故障持续期间有明显优势。当故障恢复时，次暂态电抗的减小也对恢复期间的过电压有微小的改善作用，这是由于次暂态电抗减小后，虚拟d轴阻尼绕组的虚拟电感和电阻值改变，使得其磁链抵御故障所产生的下降趋势有更为明显的效果，从而使得d轴总磁链抵御故障的能力也更强。由于端电压主要取决于d轴磁链，因此d轴磁链的缓慢下降将会对端电压的支撑有着较强的正面影响。次暂态电抗减小后，机组吸收和发出无功的能力也相对增强。故障期间和故障恢复后，不同次暂态电抗情况下逆变器的输出无功如图8 所示。可以看出，当次暂态电抗减小时，故障瞬间和故障持续期间发出的无功会大幅提升，为电压提供强有力的支撑作用，而当故障恢复之后，较小的次暂态电抗又会使得逆变器吸收更多的无功，以缓解恢复期间的过电压现象。以上表明，较小的次暂态电抗对于电压支撑有着可观的正面作用。然而，次暂态电抗不能过小，否则系统将会无法进入初始的稳定状态。

图6 不同次暂态电抗参数下的故障期间端电压瞬时值

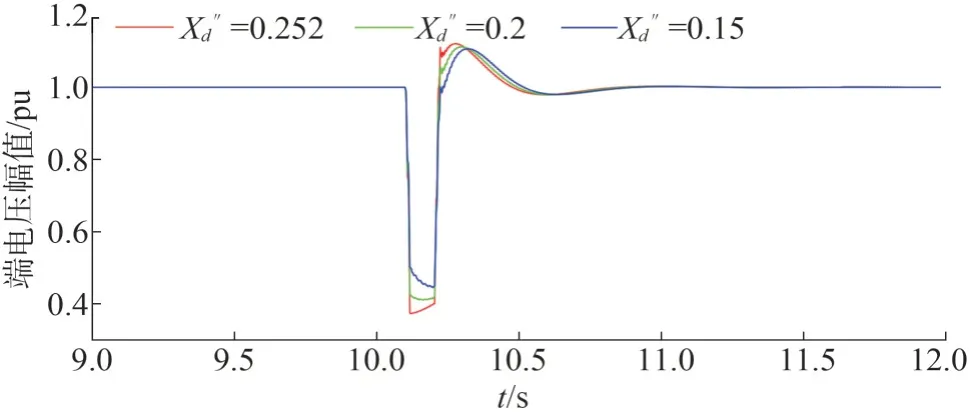
图7 不同次暂态电抗参数下的故障期间端电压幅值

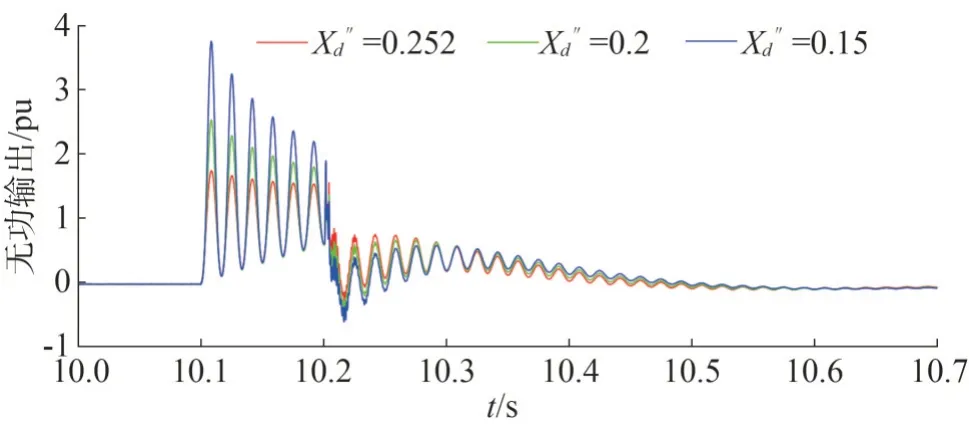
图8 无功输出

图9 故障过程中虚拟d轴磁链

图10 故障过程中虚拟q轴磁链

图11 故障过程中虚拟d轴阻尼绕组磁链

4.2 虚拟调相机控制的惯量支撑作用研究

为了研究控制策略的惯量支撑作用，需观察不同惯量时间常数下的频率响应。改变初始的惯量时间常数分别为3.2 s、2.5 s 和2 s，并观察故障期间的虚拟转速波形。不同惯量下，虽然故障持续期间有功出力不变，但较大的惯量意味着较好的稳定性，因此惯量较大的情况下故障期间虚拟转速波动较小。而在故障恢复期间，较大的惯量也对平抑功率和转速的波动有较好的抑制效果，但恢复至初始值的时间也会增加，仿真结果如图12和图13所示。实际工程中应选择合理的惯量参数，以获得最佳的频率响应效果。

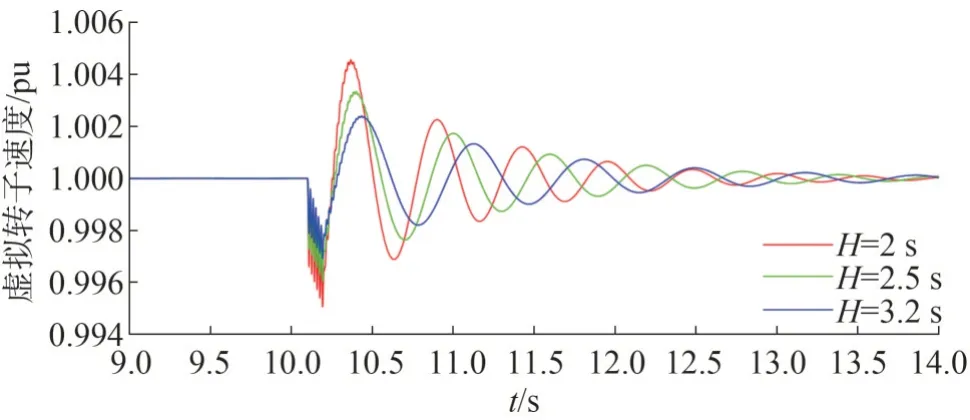
图12 不同惯量时间常数下虚拟调相机转速

图13 不同惯量时间常数下虚拟调相机有功输出

5 结语

新能源场站建设位置普遍分散，提出了一种将逆变器模拟为同步调相机的控制方式，相当于在区域中各个新能源场站附近分布式接入多台小容量调相机，因此可以比集中接入更好地解决暂态工况下的电压稳定问题，也可以一定程度上减小使用传统调相机带来的运输、维护成本以及噪音、旋转磨损等问题。不仅如此，相比于实物调相机需要在制作工艺上进行改进以优化各种参数来说，提出的虚拟调相机仅需调整一些控制参数即可，在保证对电网提供一定的电压稳定支撑和频率稳定支撑的前提下，大幅降低了成本并提高了便捷性。

所提方式通过模拟同步电机的次暂态效应和转子方程，为电网提供短路故障下的强电压支撑能力和惯量支撑。仿真结果表明，次暂态电抗的适度减小和惯性常数的增大更有利于短路故障期间的电压支撑和频率稳定。将此控制策略应用于新能源逆变器大规模接入的地区，可以赋予逆变器与同步调相机类似的电压支撑能力和频率支撑能力，以适当减少对于调相机的依赖和调相机的部署及制造成本，对于电网的经济运行和控制有着更好的作用。但是，对虚拟同步调相机控制参数的精确计算存在一定的技术难度。此外，当新能源场站进行扩建或维修更换时，如何保证虚拟同步调相机主动适应新的微电网状态并提供相应的电压、频率支撑能力仍然需要进一步研究。