巧设变式 溯知本源
——2022年全国甲卷理科第20题的变式探究与思考*
2023-01-24游金凤
游金凤
(云南师范大学数学学院 650504)
黄赛春
(云南省昆明市官渡区钟英中学 650214)
刘冰楠
(云南师范大学数学学院 650504)
1 试题再现
2022年高考数学全国甲卷理科第20题(以下简称“第20题”)表述如下:
设抛物线C:y2=2px(p>0)的焦点为F,点D(p,0),过F的直线交抛物线C于M,N两点.当直线MD垂直于x轴时,MF=3.
(1)求抛物线C的方程;
(2)设直线MD,ND与抛物线C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别为α,β,当α-β取得最大值时,求直线AB的方程.
评析该题综合考查直线、抛物线、三角函数、均值不等式的基本概念和性质,渗透数形结合、函数与方程等思想方法,着力考查学生的数学运算、逻辑推理和数学抽象等核心素养.其中,第(1)问属于圆锥曲线的常规题型,需根据已知条件列方程、解参数、得抛物线方程,注重基础知识的考查;第(2)问涉及直线、抛物线、三角函数和均值不等式等基础知识的综合考查,要求考生在较为复杂的直线与抛物线的位置关系中,抓住解决问题的本质,突出基础知识内在联系和综合运用的考查,对考生思维灵活性的要求较高,该题不仅利于数学高考选拔功能的发挥[1],也利于检验学科素养和关键能力.

图1
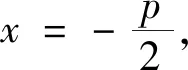





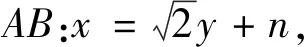
2 变式延伸
圆锥曲线的定点定值问题是高考数学的命题热点,常以函数、方程、不等式等为知识背景,以圆锥曲线和直线为桥梁,深入考查学生的运算求解能力、逻辑思维能力等关键能力.圆锥曲线的定点定值问题考查知识点范围广、运算量大、综合性强,但考查题型和解题方法有迹可循.因此,以“第20题”第(2)问为“生长点”,通过变式探究抛物线定点定值问题,既发挥一题多变的功效,也达成多题归一的成效[2].
2.1 定点问题
定点问题的数学本质是在动直线中找不动点,即定点.解决该类问题主要有两种解题思路:一是找特殊值,根据题目已知条件寻找所求直线的特殊情况后猜想定点,或结合图象的特点与性质找定点,再进行推理论证;二是通过求出直线方程,根据方程中参数之间的关系找出定点.若直线方程为斜截式y=kx+b,则需根据已知条件找k与b之间的等量关系,进而得到定点;若直线方程为点斜式y-y1=k(x-x1),根据直线方程表达式即可得出定点.在解题过程中,可通过巧设点和直线的方程来减少计算量,避免分类讨论.本文不改变“第20题”题干中的已知条件,仅对第(2)问的题设和结论进行变式.
变式1设直线MD,ND与抛物线C的另一个交点分别为A,B,证明直线AB经过定点.

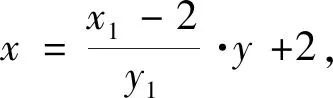


图2
变式2如图2,设直线MD,ND与抛物线C的另一个交点分别为A,B,求证:以AB为直径的圆经过定点O(坐标原点).



[y-(y1+y2)]2=16(1+4m2)·(1+m2),即[x-(8m2+4)]2+(y-4m)2=16(1+4m2)·(1+m2).
化简得x2-(16m2+8)x+y2-8my=0,由方程可知,以AB为直径的圆过定点(0,0).
评析变式1和变式2是圆锥曲线定点问题的常规考法,根据题目已知条件设点和直线方程,再将直线方程与抛物线方程联立,利用韦达定理得出y1y2,y1+y2的值,根据直线斜率公式和巧设直线MD方程得出y3,y4分别与y2,y1之间的等量关系,进而得出A,B坐标,最后根据两点式和两点间的距离公式分别得到AB的直线方程(变式1)和AB的长度(变式2),进而根据方程表达式即可判断恒过的定点.两道变式简化了原试题,降低了运算量,是定点问题的常规模型;但变式2相较于变式1,是对定点问题的进一步拓展和延伸.在常规模型的基础上适当联结直线、抛物线、圆等多方面知识,丰富题型设置,这不仅利于学生体会该类问题的通性通法和知识间的内部衔接,也利于数学运算、逻辑推理等核心素养的提升以及分析问题、解决问题能力的发展.
2.2 定值问题
定值问题就是在运动变化中寻找不变量的问题,其问题的本质是求出定值[2].常见的解题方法主要有两种:一是将题目条件的特殊值作为切入点,求出定值,再验证该值不受运动的影响;二是直接设点的参数或直线斜率的参数,通过消除变量简化运算,进而得到定值.在不改变“第20题”题干中的已知条件,仅对第(2)问的题设和结论进行变式.
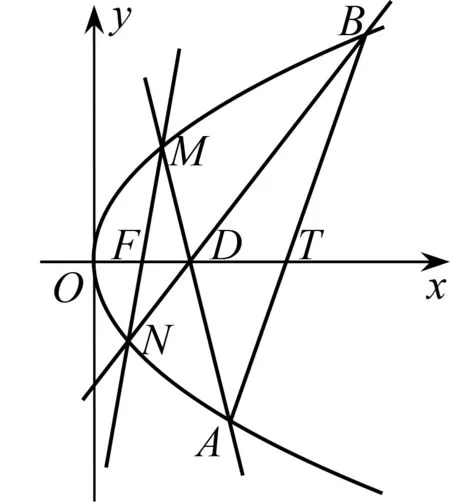
图3
变式3如图3,设直线MD,ND与抛物线C的另一个交点分别为A,B,求证:△DMN与△DAB的面积之比为定值.



图4
变式4如图4,设直线MD,ND与抛物线C的另一个交点分别为A,B,过点A,B分别作抛物线C的切线,两切线交点为P,证明点P在定直线上.


评析变式3和变式4考查圆锥曲线定值问题中的面积比、定直线问题,其前部分的解题过程与变式1相同,不同点在于求得A,B坐标之后,变式3涉及直线、抛物线、三角形面积公式、点到直线的距离公式和两点距离公式等基础知识的综合考查,既不失题型的基础性,又凸显压轴题的综合性;变式4是证明点在定直线的特殊定值问题,体现直线、圆锥曲线、导数等知识的横纵联系.该类型题目对学生思维的灵活性提出更高要求,能有效训练思维的敏捷性.对高考圆锥曲线试题进行“再创造”,进而探寻定值一类问题的解题思路与方法,回归本源命题热点,体会其中蕴含的数形结合、函数与方程等数学思想,促进数学运算、逻辑推理、数学建模和数学抽象等核心素养的提升.
3 教学建议
通过以上分析,对圆锥曲线常考题型——定点定值问题提出以下教学建议.
3.1 巧变题源,提升效能
著名数学教育家弗赖登塔尔指出:“数学教育方法的核心是学生的再创造.”[3]而一类问题通性通法的学习,利于从整体上培养学生的学科思维、能力、素养,是基本思想与活动经验的重要获取途径,是长久、可复制的学习经验[4].通过对高考圆锥曲线试题的再加工再创造,既能探寻抛物线定点定值问题的通解通法,帮助学生领悟其中蕴含的数学思想方法,提升数学运算、逻辑推理等核心素养,又能拓宽知识的网络体系,体会知识的整体性.因此,教师在教学过程中针对高考试题进行拓展变式,延伸知识,能有效探寻其数学本质,发现知识的内在联系,也能发挥高考“引导教学”功能[5]28,提升高考的教育教学效能.
3.2 多向探析,回归本源
高考试题命制强调数学内容的基础性、综合性[6],同时也强调“不同层面知识的纵向融会贯通,体现知识之间具备的内在逻辑联系”[5]30.一道高考数学试题蕴含多个知识间的横纵联系,“找出知识的源头、寻求正确的关联点是解决问题的关键”[7].圆锥曲线定点定值问题是高考命题热点,这类问题常被用来与直线、圆与方程、导数、不等式、三角函数等知识一起进行综合考查,渗透多种数学思想与方法,能有效发挥数学高考的选拔功能.因此,教师在教学中应有意识对高考题进行深入剖析,以一题为知识的衍生点,多向探析与不同知识间的内部联系,既利于帮助学生回归知识考查的数学本质,淡化解题技巧,消除解题固化思维,也利于教师把握高考命制的方向,达成触类旁通、举一反三的教学成效.
3.3 以考促思,强化素养
2022年高考数学命题坚持学科素养导向,注重基础知识、关键能力与思维品质的考查,有效落实立德树人根本任务.“第20题”圆锥曲线问题融汇多个知识点间的综合考查,对学生的数学思维、数学素养均提出了更高要求.教学中教师应深入剖析高考题的命制特点,“准确把握高考数学考查的内容和要求,灵活分析和运用不同类型的试题情境”[8],注重教学反思,把握高考试题命制新样态,以此促进教与学的不断“生长”.对高考题源进行变式延伸,探析知识考查的数学本质.这不仅利于“优化思维品质,发展创新能力”[9],也利于强化数学运算、逻辑推理、数学建模和数学抽象等核心素养的培养.
