对角修形斜齿轮高精度逆向建模

李旭东 ，魏 刚

（长安大学工程机械学院，陕西 西安 710064）

0 引言

斜齿轮因具有承载能力强、重合度大、传动平稳的特点，在农机产品、新能源汽车、风电设备等齿轮传动场合得到广泛应用。但由于安装误差和制造误差等因素影响，轮齿啮合时会产生啮入冲击，导致振动和噪声。而对角修形是实现减振降噪的有效方法。因此，完成对角修形斜齿轮的精确建模对啮入冲击力计算、齿面承载接触分析和有限元仿真分析等有重要意义。

王宪法等[1-2]最早提出对角修形方法，并通过试验证明对角修形斜齿轮相较标准齿轮具有更低的噪声。蒋进科等[3]通过仿真计算表明，对角修形相较齿廓修形在实现斜齿轮减振降噪方面效果更显著。何湘玥[4]基于Masta平台通过仿真计算发现，对角修形斜齿轮可降低电动汽车的啸叫。曾红等[5]基于CATIA逆向工程完成弧齿锥齿轮建模，并通过无缝接口导入ABAQUS完成接触应力分析，该方法可提高分析效率。高晓伟等[6]基于CATIA对弧齿锥齿轮进行了建模，并将其导入ABAQUS完成应力分析，仿真应力和Hertz接触理论计算应力基本一致，验证了建模合理性。葛德等[7]研究了基于MATLAB和CATIA完成标准斜齿轮快速精确建模的方法。唐良兵等[8]基于CATIA建立斜齿轮三维模型，并完成了应力分析，试验结果与仿真结果基本吻合，表明了建模的可靠性。金美付等[9]基于CATIA完成齿向鼓形修形斜齿轮建模，最高可达0级精度。Fuentes-Aznar等[10]提出采用Hermite插值方法实现非光滑连接齿根过渡区的几何建模。

CATIA在齿轮建模方面具有较高的精度，在实际工程中应用非常广泛。基于CATIA完成对角修形斜齿轮的精确建模，对结构设计、CAE快速分析等有重要意义。本研究首先以斜齿轮为研究对象，建立假想产形斜齿条展成斜齿轮坐标系，推导出标准工作齿面和齿根过渡齿面方程。其次，给出对角修形方法的具体过程，在标准工作齿面法矢方向叠加修形曲面建立修形齿面，并利用Hermite插值对修形齿面与齿根过渡曲面的边界处进行光滑处理。最后，借助CATIA完成对角修形斜齿轮的三维逆向建模和拟合偏差分析。

1 全齿面方程

1.1 标准渐开线

假想产形齿条展成工件右齿面的坐标变换如图1所示，建齿条刀参考坐标系St于左刀面，通过坐标变换即可得到左齿面。图中αn为法向压力角，β为分度圆螺旋角，θ1为齿轮转角，rp1为分度圆半径；am=0.25πmn/cosβ，表示1/4端面齿距；mn表示齿轮法向模数。假设齿条刀右侧刀面位矢和单位法矢分别为rt=[ut, 0,lt, 1]T，nt=[0, 1, 0]T，其中ut、lt分别为齿条刀右刀面xt轴、zt轴上的坐标参数。根据齿轮啮合原理，标准渐开线右齿面的位矢r1(ut,lt,θ1)、单位法矢n1(ut,lt,θ1)以及啮合方程[11]表示为：

图1 假想产形齿条展成工件右齿面的坐标变换

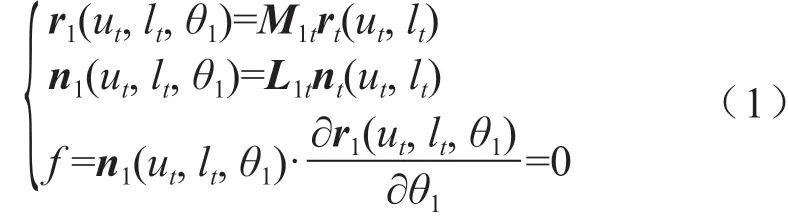
式中，M1t=M1fMfaMabMbcMcdMdt，M1t为从齿条刀参考坐标系St到工件动坐标系S1的变换矩阵，L1t为M1t去掉最后一行和最后一列的变换子矩阵。

1.2 齿根过渡曲线

假想产形齿条法向齿廓如图2所示，假设齿条过渡圆弧部分的位矢和法矢分别为r＇t=[-rwsinφtmntanαn,rwcosφt-rw,lt, 1]T，n＇t(φt,lt)，其中过渡圆弧半径rw=0.25mn/(1-sinαn)。根据齿轮啮合原理，工件右侧齿根过渡齿面的位矢r＇1(φt,lt,θ1)、法矢n＇1(φt,lt,θ1)及啮合方程为：

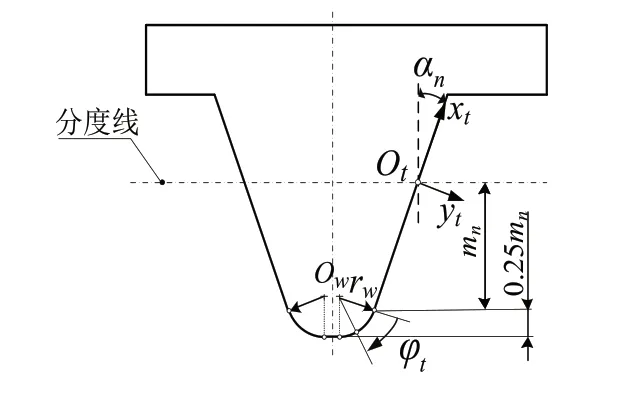
图2 假想产形齿条法向齿廓

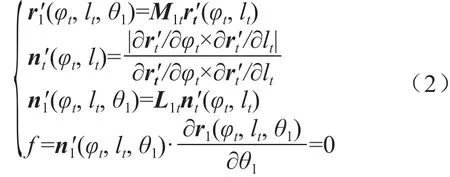
式中，φt∈[0, π/2-αn]。

2 对角修形齿面建模

对角修形是指在轮齿啮入啮出端进行修形，中间部分不修或者少修。以右旋斜齿轮左齿面为例进行分析，对角修形斜齿轮三维图如图3所示。齿顶修形终止位置为齿顶ra1，齿根修形终止位置是在保证渐开线最小啮合长度条件下的啮合起始点，其半径rk1为：

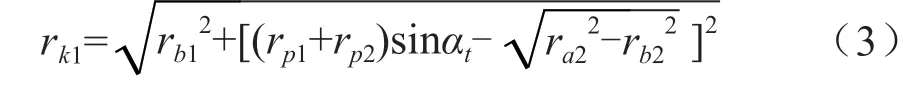
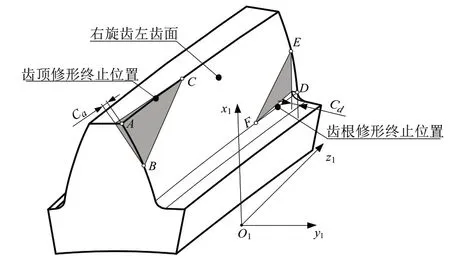
图3 对角修形斜齿轮三维图

式中，ra2为从动轮的齿顶圆半径，rb1、rb2分别为主、从动轮的基圆半径，rp1、rp2分别为主、从动轮的分度圆半径，αt为端面压力角。旋转投影面对角修形示意图如图4所示，给定修形高度AB、DE，得到旋转投影面上B点坐标（-B1/2，ra1-AB）、E点坐标（B1/2，rk1+DE），其中，B1为齿宽，可以得出：

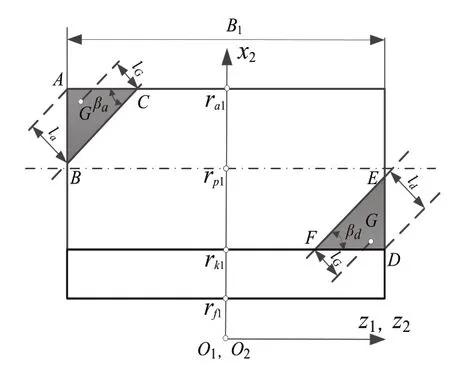
图4 旋转投影面对角修形示意图

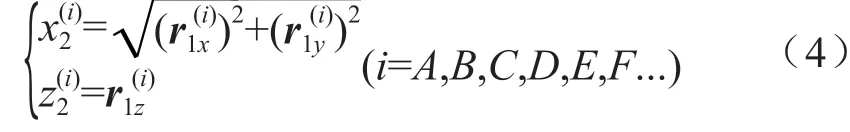
联立式（1）（3）（4）分别得到B、E点的齿轮转角根据同一齿面接触线齿轮转角相同的原理，将分别代入式（1）（3）（4）得到修形长度AC、DF。修形起始线BC、EF在旋转投影面上的投影非常接近直线，为便于修形量的计算，用直线代替曲线。齿顶、齿根修形起始线的螺旋角分别为βa=atan(AB/AC)、βd=atan(DE/DF)。假设齿顶和齿根修形区域内任意一点G到修形起始线的距离为lG，修形区域沿着lG方向的修形量可按照直线型、二次抛物线、四次抛物线增大，且平行于修形起始线的修形量相等，则点G(z2,x2)的修形量为：

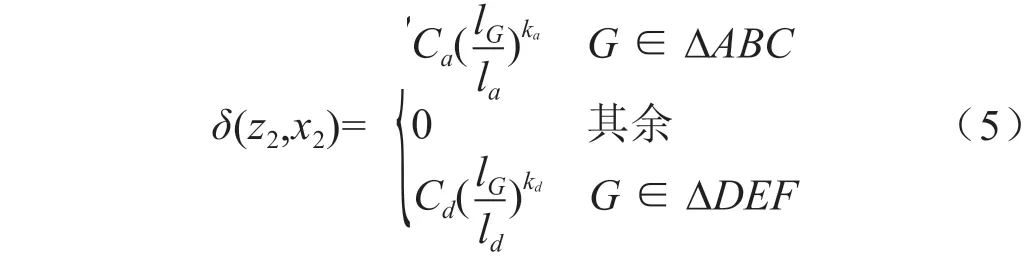
式中，Ca、Cd分别为齿顶和齿根的最大修形量；ka、kd为修形曲线次数，可取1次、2次、4次；la为A到BC的距离；ld为D到EF的距离。

修形齿面表示为标准渐开线齿面与法向修形曲面的叠加，其位矢和法矢可表示为：

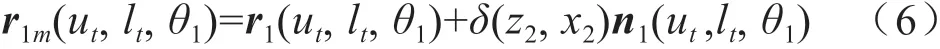
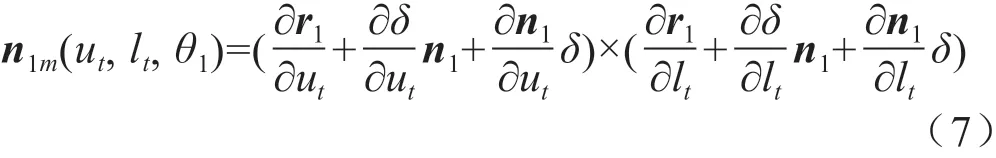
式中，r1m，n1m分别为小轮对角修形齿面的位矢和单位法矢。

图3中修形齿面与齿根过渡曲面的边界处出现不连续问题。而Hermite插值不仅可以保证在给定节点处插值多项式的函数值与原函数值相同，而且可以使其导数值也与被插函数的相应阶导数值相等，非常适合用于对不连续处进行光滑处理，如图5所示。给定位矢P0、P1以及切矢T0、T1，通过式（8）定义两点之间的Hermite曲线[10]为：

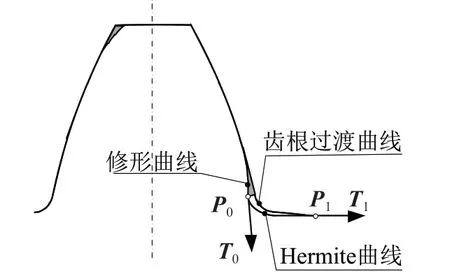
图5 Hermite插值处理修形曲线与过渡曲线分界处

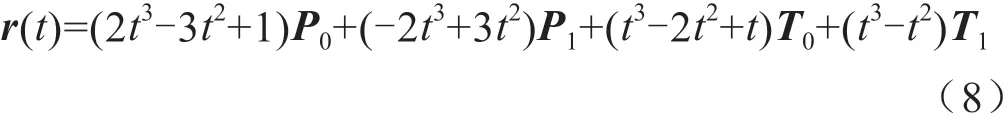
式中，t为Hermite曲线参数，t∈[0,1]。可以得出Hermite曲线的混合函数：

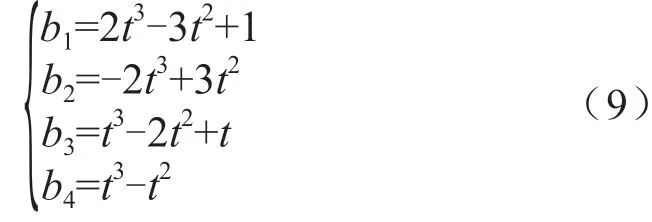
式中，b1、b2、b3和b4为权重系数。

进行修形齿轮Hermite曲面建模时，针对齿轮某一截面的过渡曲线，假设初始点位矢P0为(xP0,yP0,zP0)，最终点位矢P1为(xP1,yP1,zP1)，初始点P0的切矢T0为(xT0,yT0,zT0)，最终点P1的切矢T1为(xT1,yT1,zT1)。则Hermite曲线上一点P(xP,yP,zP)关于参数t的函数为：

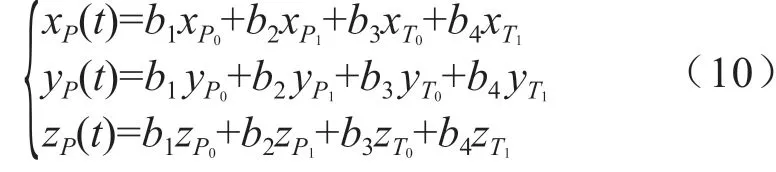
Hermite曲线曲率是变化的，需增加切向量参数th控制曲线的弧度，th的取值范围一般为0.5~1.5。对切矢T0和T1分别乘以齿轮法向模数mn以及切向量参数th，通过调整th得到满足要求的齿轮轮廓。

3 逆向建模和精度分析

斜齿轮副基本参数和对角修形基本参数分别如表1、表2所示。为保证Hermite曲面与原齿根过渡曲面较为逼近，经多次调整发现取th=0.9效果最好。通过MATLAB编程对二次抛物线对角修形斜齿轮齿面在齿高方向和齿宽方向进行数字化离散，如图6所示；其中Hermite插值处理后的斜齿轮右侧前端面曲线廓形如图7所示。

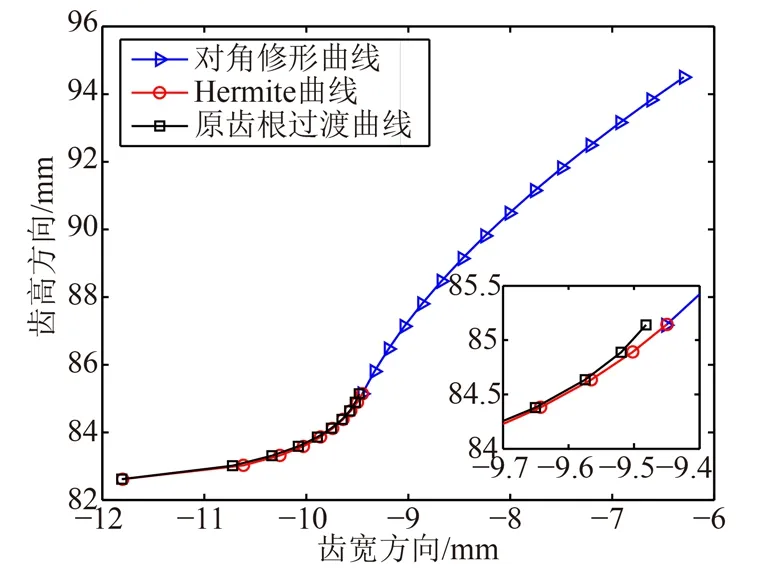
图7 斜齿轮右齿面前端面曲线廓形

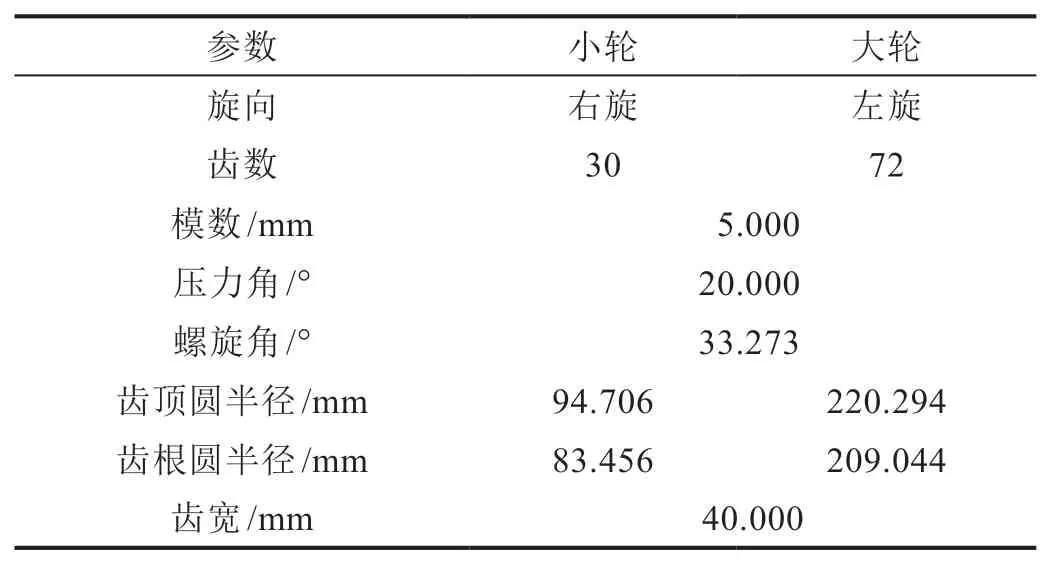
表1 斜齿轮副基本参数

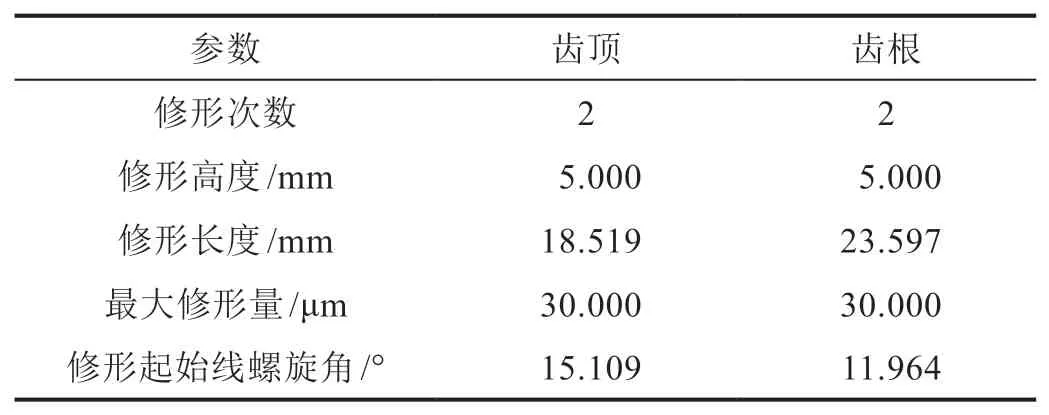
表2 对角修形基本参数

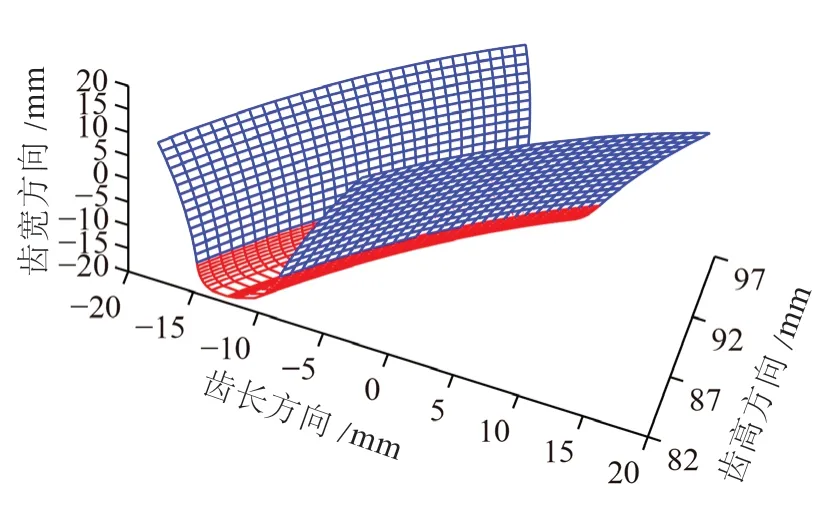
图6 二次抛物线对角修形斜齿轮齿面

利用CATIA中DES模块import命令将齿面离散坐标点数据导入形成点云，通过QSR模块的Power fit命令进行强力拟合得到单个齿槽。借助DES模块的Deviation Analysis命令[12]对修形齿面和标准齿面进行偏差分析，此命令定义左侧齿面法矢方向由标准齿面指向齿槽处，右侧齿面法矢方向由标准齿面指向实体。在齿廓方向，分别选取z1为-20 mm、0 mm、20 mm处截线每次导入50个标准齿面点计算偏差。左右齿面齿廓偏差如图8（a）、（b）所示，z1分别为-20 mm、20 mm时的截线偏差去除修形量30 μm，得到最大拟合偏差分别为0.189 μm、0.380 μm；而z1为0 mm的截线偏差，去除在齿根修形终止位置处的最大修形量为0.7 μm，齿根部分最大拟合偏差为0.636 μm，而此截线靠近齿顶部分不修形，则此截线最大拟合偏差为1.103 μm，发生在左齿面。因此，齿廓最大拟合偏差为1.103 μm。在齿向方向，分别选取半径r为85.666 mm（齿根修形终止位置）、89.706 mm（分度圆）、94.706 mm（齿顶圆）的截线每次导入100个标准齿面点计算偏差。左右齿面齿向偏差图如图8（c）、（d）所示，r分别为85.666 mm、94.706 mm的偏差去除修形量30 μm，得到最大拟合偏差分别为0.380 μm、0.189 μm，r为89.706 mm的截线偏差去除靠近齿根修形区域外端面上的修形量1.1 μm，而此截线靠近齿顶区域不修形，则此截线最大拟合偏差为0.691 μm，发生在右齿面。因此，齿向最大拟合偏差为0.691 μm。综上，左右修形齿面最大拟合偏差约为1.1 μm。

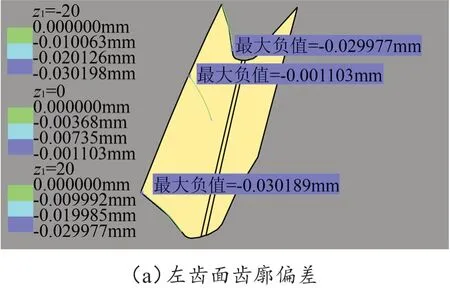
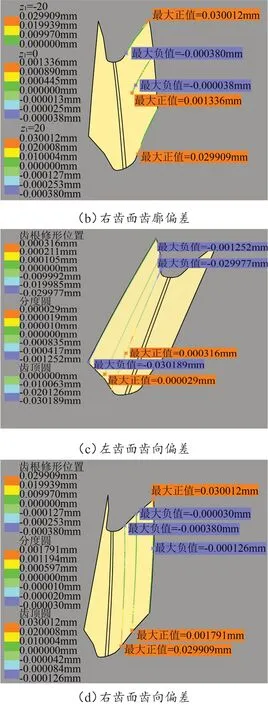
图8 二次抛物线对角修形斜齿轮偏差比较

经延伸、裁剪、封闭、旋转、阵列等命令得到二次抛物线对角修形斜齿轮三维模型，如图9所示。

图9 二次抛物线对角修形斜齿轮三维模型

4 结论

1）本文以斜齿轮为研究对象，建立假想产形斜齿条展成斜齿轮坐标系，并推导出标准工作齿面和齿根过渡齿面的齿面方程和啮合方程。

2）在标准工作齿面法矢方向叠加修形曲面建立修形齿面，并利用Hermite插值对修形齿面与齿根过渡曲面的边界处进行光滑处理。

3）借助CATIA软件完成了二次抛物线对角修形斜齿轮的精确建模，最大拟合偏差约为1.1 μm，符合设计要求。