角接触球轴承内外圈复合故障尺寸评估

陈立海，谭 奥，杨丽秀

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.中国航发哈尔滨轴承有限公司 博士后科研工作站，黑龙江 哈尔滨 150500)

0 引言

角接触球轴承故障是旋转机械重大故障的主要原因之一。为了减少轴承故障对系统造成的损害，需尽早识别故障尺寸，进而判断出故障发展到什么程度。有很多信号处理方法用来识别故障的特征频率[1]，包括小波相关滤波[2-3]、时频脊线增强[4]、固有时间尺度分解[5]、积分谱相干性[6]、谱峭度[7]以及稀疏矩阵[8]等。这些方法可以确定哪些轴承元件发生了故障，但无法反映有关故障尺寸的细节。

目前，主要有两类方法来评估故障尺寸。第一类是检测滚动体进出故障区域时产生的冲击，但是，由于振动信号存在大量噪声，这些进出冲击很难被检测到。因此，首先需要降噪处理，如预白化或最小熵反褶积(minimum entropy deconvolution,MED)[9-10]，采用小波变换方法检测进出故障区域的振动信号[11-13]。然而，虽然小波系数在某些分解水平上对脉冲信号的表征更准确，但使用它们来识别进入和退出故障区域却存在困难，因此有学者将变分模态分解(variational modal decomposition,VMD)应用于预白化后的双脉冲信号的处理，双脉冲特性用于确定滚动体进入和退出缺陷的时间，从而可以估计故障的尺寸[14]。第二类是基于振动信号统计特征参数的评估方法，认为振动信号的统计特征与故障尺寸之间存在一定的关系。例如，均方根与故障大小之间存在一定的线性关系[15-16]。文献[17]全面研究了外圈、内圈和滚动体中故障尺寸对均方根、峰值、峰值因子、峭度和电平通过率等指标的影响，并提出了故障尺寸与振动特性之间的简单联系。反向神经网络也被用于预测内圈、外圈和滚动体故障尺寸[18]。文献[19]提出了一种使用深度神经网络(deep neural networks,DNN)的高效评估方法，可以正确预测裂纹尺寸以及轴承退化水平。文献[20]提出了一种基于深度卷积网络和贝叶斯优化的诊断模型，以识别轴承故障的严重程度。文献[21]提出了一种利用离散小波包变换(discrete wavelet packet transform,DWPT)和包络分析的轴承损伤程度评估方法。上述文献中的大多数研究只关注对单个故障的定量评价，对复合故障的定量评价很少。

因此，本文采用改进的连续谐波小波包分解方法对复合故障振动信号进行分解和重构，获得与复合故障对应的内外圈单点故障信号，通过数值模拟，研究振动信号统计特征与故障尺寸之间的关系，进而获得复合故障尺寸评估方法。

1 角接触球轴承内外圈复合故障动力学模型

正常轴承动力学建模过程参照Gupta的建模方法[22]。下面重点阐述角接触球轴承内外圈复合故障的动力学建模过程。如图1所示，假设故障为圆形凹坑，内外圈故障区域直径和深度为wdi、wdo、hid、hod；θie和θoe是与内、外圈故障区域对应的中心角的一半，θid和θod分别为内、外圈受损区域中心的旋转角度，θib和θ(i+1)b分别是第i个和第i+1个球的公转角度。

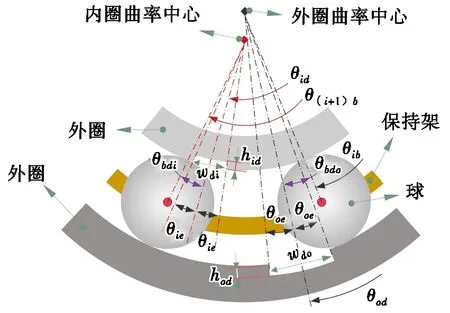
图1 球与故障区域的关系

要确定球是否进入故障区域，需计算故障区域和滚动体所对应的旋转角度[22]：

(1)

如果θbdi<θie，球进入内圈的故障区域；如果θbdo<θoe，球进入外圈的故障区域。如果球未进入故障区域，可根据文献[22]计算球与套圈的接触变形，如果进入故障区域，需要引入由故障引起的附加变形来计算接触变形，总变形量为：

(2)

接触力的方向变化如图2所示，当球进入损伤区域时，接触载荷的方向发生了变化。内圈和外圈上的接触点分别为Gi和Go，在正常轴承建模中，接触载荷的方向指向套圈的曲率中心，但是，当球进入故障区域，接触载荷方向将过Gi或Go指向球的质心。

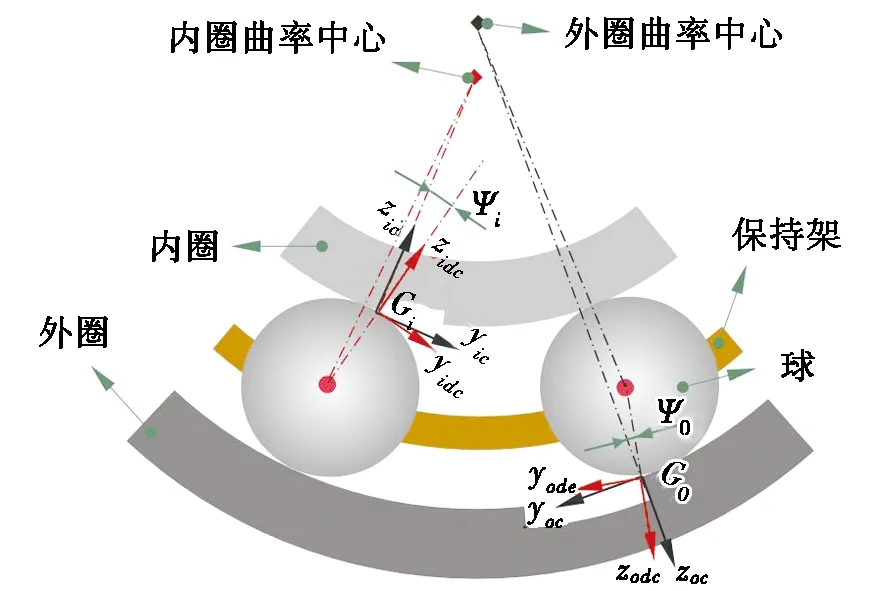
图2 接触力的方向变化

为便于描述，此处通过Gi和Go，建立故障区域接触坐标系Gi-xidc-yidc-zidc和Go-xodc-yodc-zodc，此时，接触荷载为：

(3)

进行故障动力学模型的求解过程中，需要将故障区域接触坐标系变换到正常的轴承接触坐标系。球的半径和套圈的曲率半径是已知的，轴zi(o)c和轴zi(o)dc之间角度Ψi(o)可以根据几何关系来确定，那么，该变换矩阵为：

Ai(o)dcc=A(ψi(o),0,0)。

(4)

最后采用变步长龙格库塔法对故障动力学模型进行求解，轴承的主要结构参数见表1。图3为角接触球轴承内外圈复合故障的振动信号。

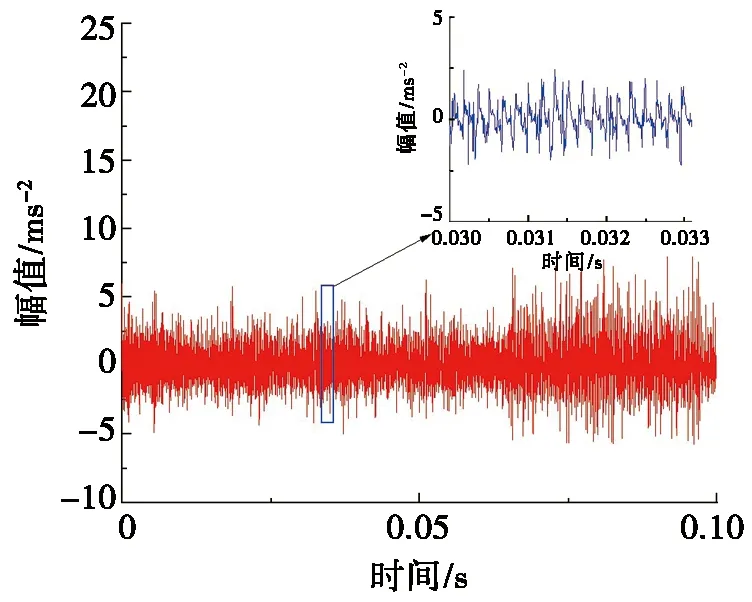
图3 内外圈复合故障振动信号

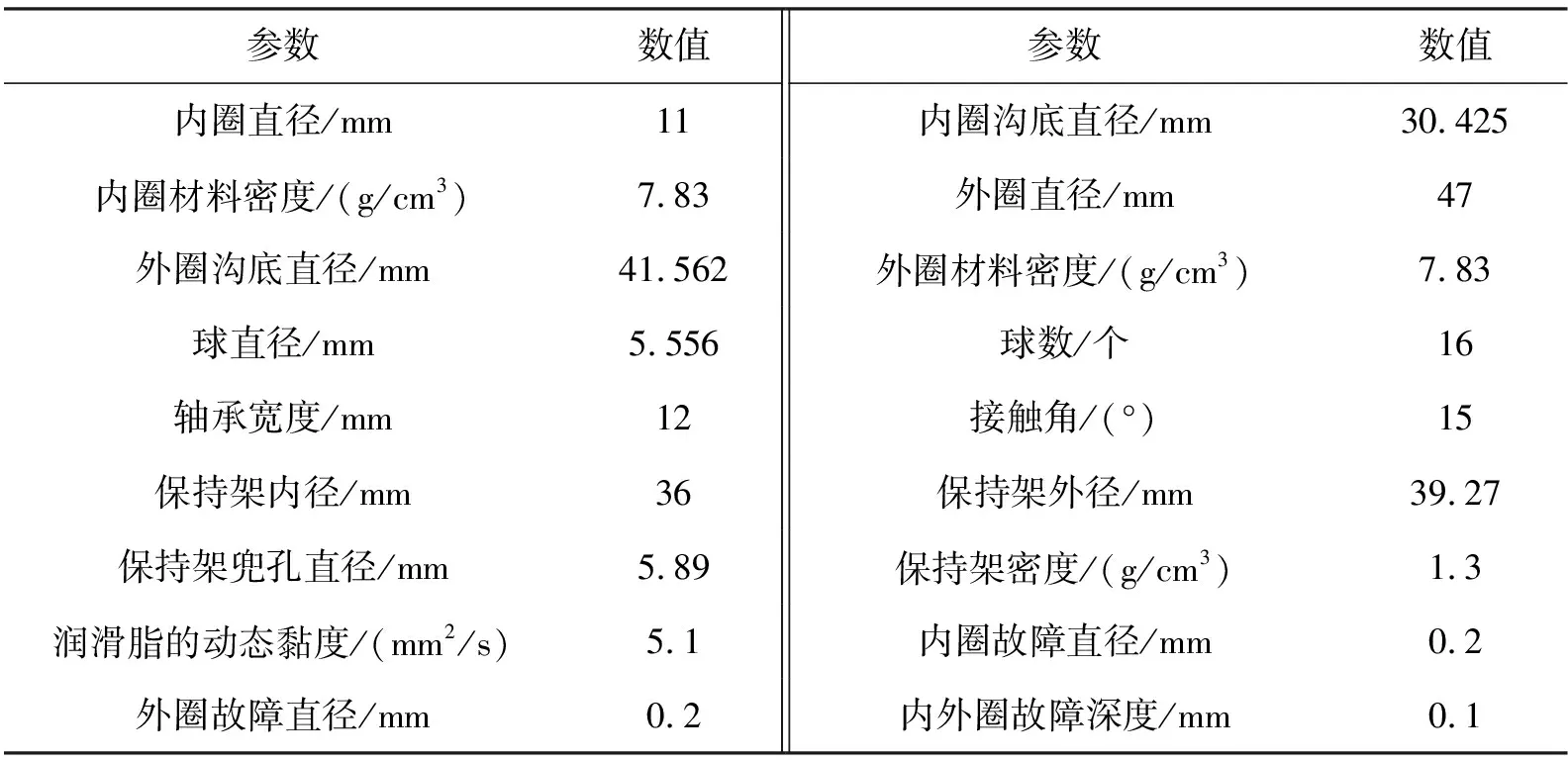
表1 轴承主要结构参数

2 轴承复合故障信号分解与重构

对复合故障信号进行分解与重构，获得与复合故障信号相对应的单点故障信号(认为复合故障信号由其所对应的单点故障信号叠加而成)，以便后续对故障尺寸进行评估。

2.1 改进的连续谐波小波包分解

在谐波小波分解中，尺度函数m和n决定了小波分解层的数量。随着分解层的增加，低频频带的细化能力得到提高，但高频频带的分辨率会降低。因此，许多研究使用二进谐波小波包分解来实现对信号频带的任意细化。

B=fh/2j,

(5)

其中：B是分析带宽；fh是该信号的最高分析频率。相应的分析频率带宽的上、下限为：

(6)

谐波小波包分解的频域分布如图4所示。随着分解层的增加，采用二进制分解方法会导致小波包分解后的子带数量和带宽范围受到限制，不能任意选择感兴趣的带宽范围。

图4 谐波小波包分解的频域分布[23]

为了消除二进制分解对子带个数和带宽范围的限制，可以通过改变m和n的值来实现信号频带的任意细分，从而得到一个有用的频带范围。图5显示了该方法的分解过程。

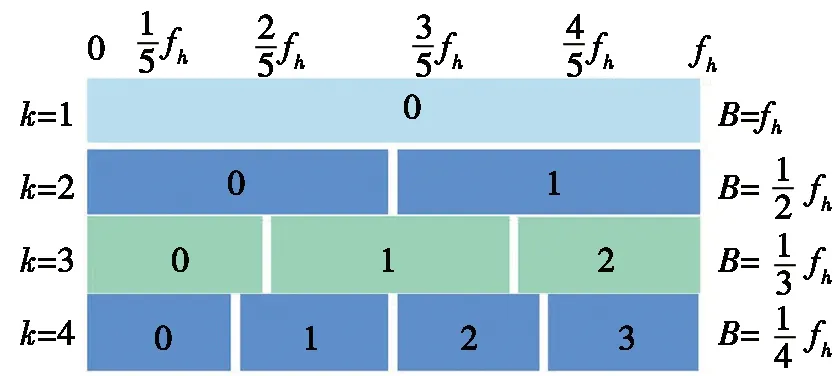
图5 改进的连续谐波小波包分解的频域分布

分解步骤如下：

根据故障频率的可能范围，确定待分解的信号x(t)的层数k，对应的子带宽为：

B=fh/k。

(7)

子带宽对应的上下限为：

(8)

各子带的谐波小波的频域表达式为：

(9)

其中:N为信号长度;fs为采样频率。

为保证分解后的谱幅与原谱的谱幅相同，定义了振幅修正系数4π(n-m)，分解后的谱为：

X′(f)=4π(n-m)X(f)Wm,n(ω)。

(10)

对方程(10)进行傅里叶反变换，得到了连续谐波小波包k层的分解子带信号。

2.2 复合故障分解与单点故障重构

角接触球轴承内外圈复合故障信号可以描述为：

(11)

其中:I为轴承故障数;si(t)为第i个故障源信号;pi为复合故障信号中第i个故障源信号的权重系数。

复合故障的谐波小波包分解步骤为：

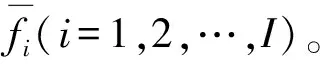
(Ⅲ)调整k层分解的谐波小波的尺度参数m和n，得到k个子带信号，表示为：

{x1(t)，x2(t)，…，xk(t)}。

(12)

经过谐波小波包分解后，第j个子带信号xj(t)可视为以下形式的调制信号：

xj(t)=aj(t)cos[φj(t)]。

(13)

那么，xj(t)的能量算子表示为：

(14)

xj(t)的瞬时振幅为：

(15)

xj(t)的瞬时幅值谱可以通过对瞬时幅值进行频谱分析得到。经能量算子解调后，可以得到各单点故障的特征频率，复合故障中每个单点故障特征频率所对应的峰值占子带整个包络谱值的比例，即该单点故障信号在这个子带信号中的权重因子，可表示为：

(16)

各子频带中的单点故障信号可以表示为：

sa,i(t)=ra,ixa(t)。

(17)

通过叠加每个子带中代表同一单点故障源的信号，可以得到单点故障信号：

(18)

采用上述方法对角接触球轴承的复合故障信号进行分解重构，得到与复合故障对应的外圈单点故障信号(如图6所示)和内圈单点故障信号(如图7所示)。

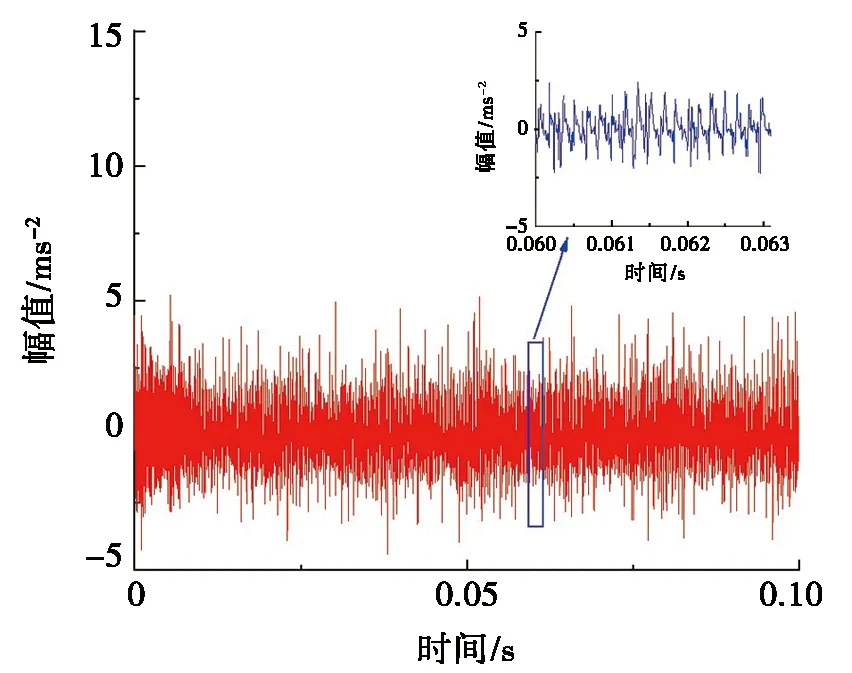
图6 重构的外圈单点故障振动信号

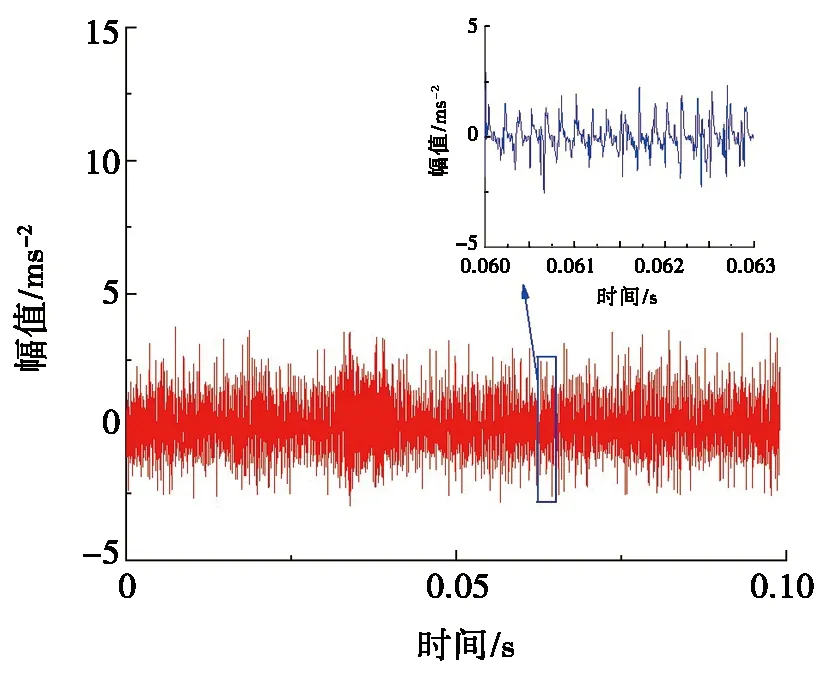
图7 重构的内圈单点故障振动信号

内外圈单点故障频率的理论值为：

(19)

其中：Z为滚动体个数；n为转速，r/min；Dw为滚动体直径,mm；dm为轴承节圆直径,mm。通过计算，内圈故障频率理论值为1 532.1 Hz，外圈故障频率理论值为1 134.6 Hz。

对重构的单点故障信号进行包络谱分析，获得了外圈和内圈故障特征频率及其倍频，如图8和图9所示，由图8和图9可以看出：故障特征频率明显，与理论计算结果基本一致，证明该方法是有效。

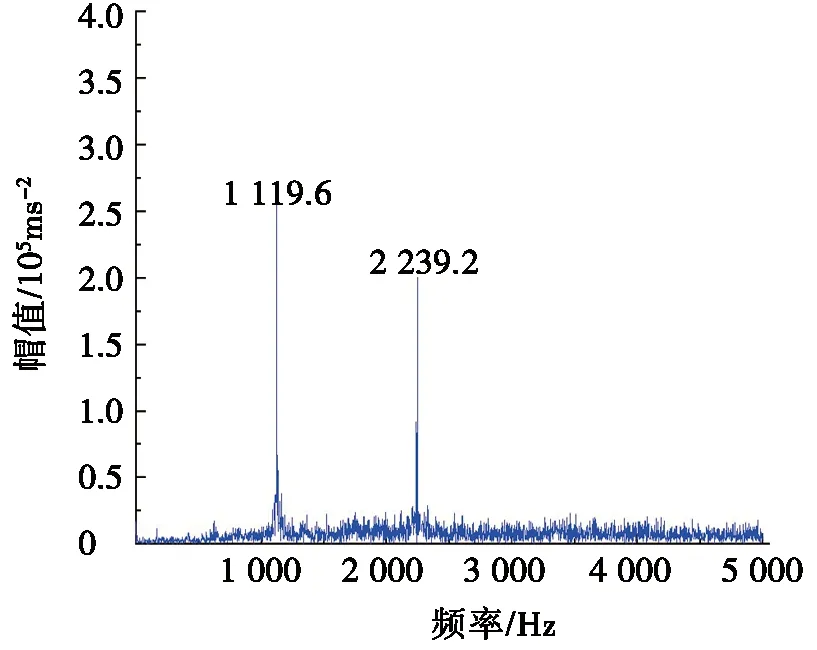
图8 外圈单点故障的包络谱

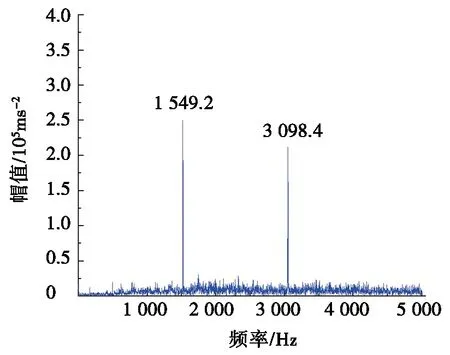
图9 内圈单点故障包络谱

3 故障尺寸评估

本节基于角接触球轴承复合故障动力学模型仿真结果和故障信号分解重构方法，探索故障尺寸由小到大(1～13 mm)过程中，故障信号统计学特征参数的演变规律，从而定量评估故障尺寸(主要讨论故障尺寸的影响)。本文研究的统计特征参数有：均方根、峭度和电平通过率。

图10为均方根随故障尺寸的变化情况。整体上均方根随着故障尺寸的增加而增加，但对于外圈故障，当故障尺寸超过6 mm时，会呈现出非线性。而对于内圈故障，变化发生在4 mm处。

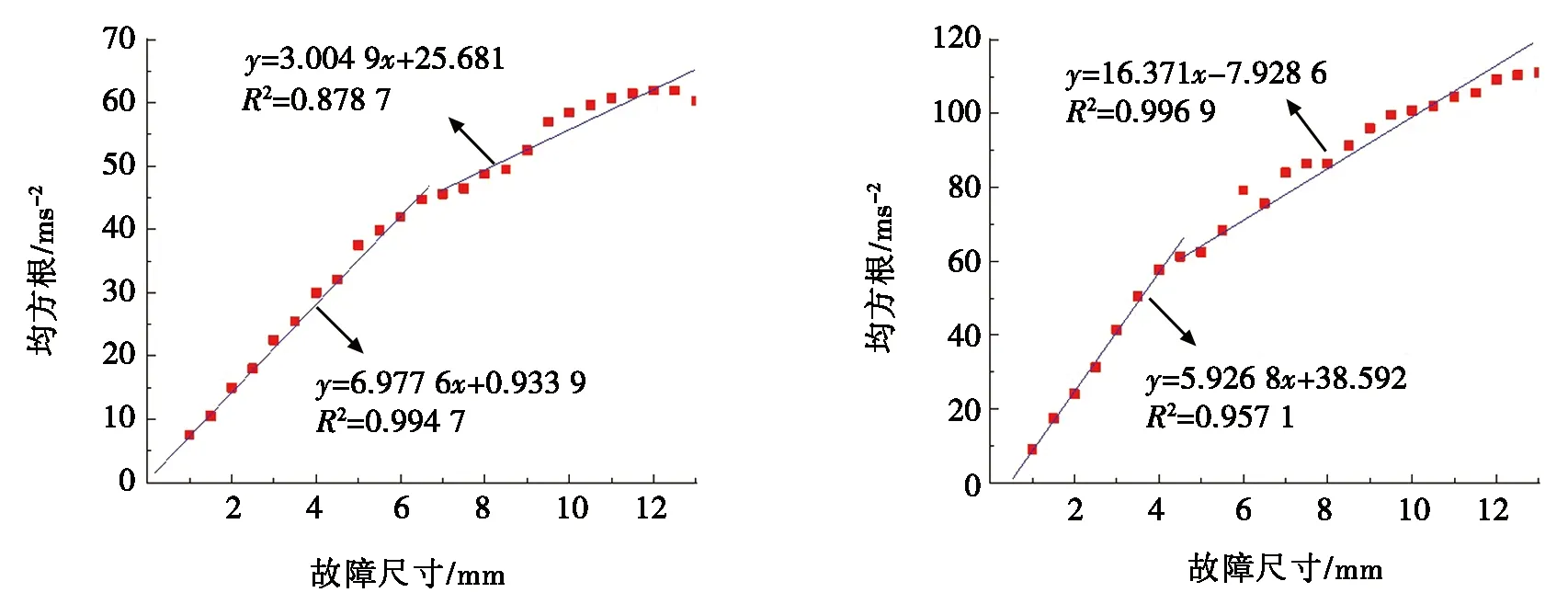
(a) 外圈缺陷 (b) 内圈缺陷

图11为峭度随故障尺寸的变化规律，一旦故障开始增长，峭度就会迅速跳跃到一个高值，而后开始下降，最后基本保持不变，线性关系不明显。外圈故障于6 mm处趋于不变的位置，内圈故障则始于4 mm处。

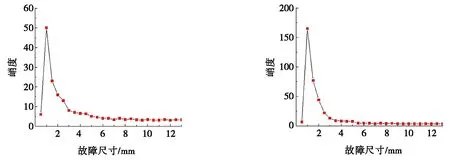
(a) 外圈缺陷 (b) 内圈缺陷

图12为电平通过率与故障尺寸之间的关系。如图12所示，电平通过率与故障尺寸之间在一定范围内存在较强的线性关系。对于外圈故障，电平通过率随故障尺寸线性增加，直到达到6 mm，电平通过率继续线性增加，但斜率较低。对于内圈故障，转折点发生在4 mm处。

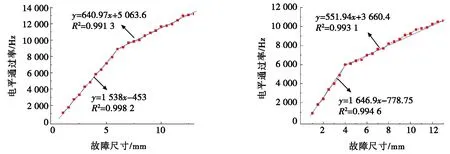
(a) 外圈缺陷 (b) 内圈缺陷

4 讨论和验证

由3个统计特征参数随故障尺寸的变化规律可知，均方根可以反映内外圈故障尺寸的变化，但超过临界点后不再适用。电平通过率能更好地反映故障尺寸的变化，表现出良好的线性关系，但要注意拐点的存在。峭度随故障尺寸的变化而剧烈振荡，线性关系不显著，但可以定性地描述故障尺寸的变化。

为了验证上述结论的有效性，进行了一系列的试验研究。图13为轴承试验台及其结构示意图，主轴支撑在两个轴承组上，试验轴承布置在一端，主轴的旋转由电机驱动，试验台还包含径向和轴向载荷施加装置，依靠液压缸来实现加载，轴承试验运行参数如表2所示。

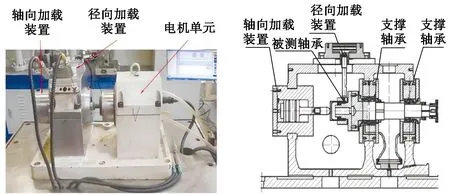
(a) 试验装置实体 (b) 试验装置结构图

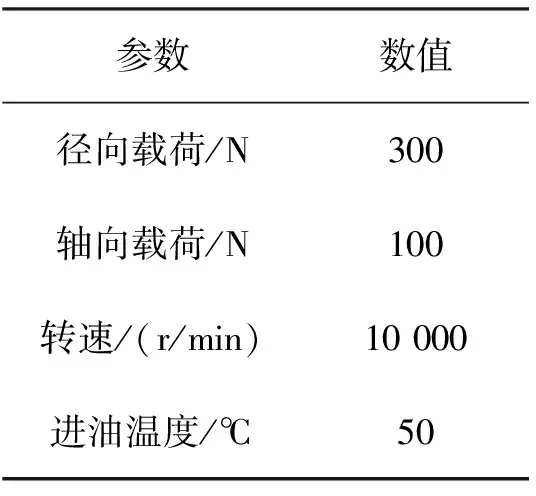
表2 轴承试验运行参数

如图14和图15所示，蓝色为试验数据点，红色为仿真数据点，试验结果与仿真结果存在一定的误差，但已相当接近，证实了均方根和电平通过率相对于内外圈故障尺寸的变化较为敏感，且在一定范围内存在线性相关，说明二者可以用于评估轴承故障尺寸的变化。

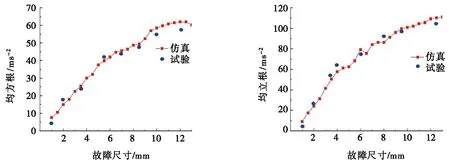
(a) 外圈缺陷 (b) 内圈缺陷

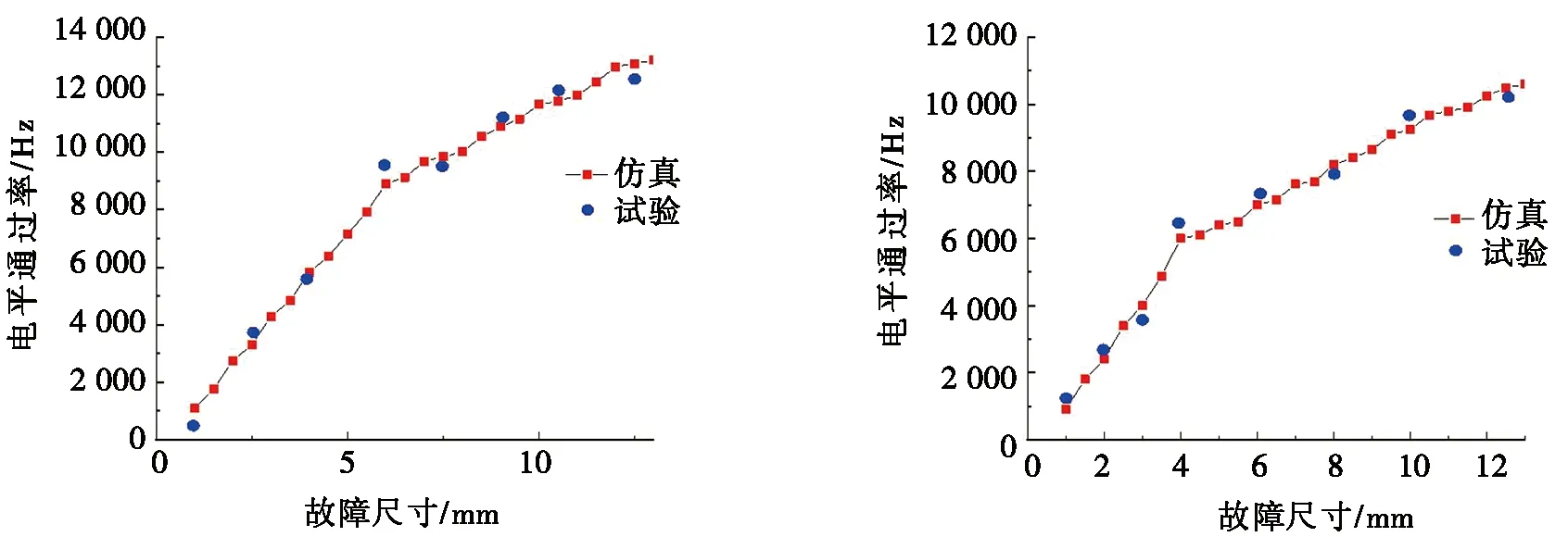
(a) 外圈缺陷 (b) 内圈缺陷

5 结束语

本文建立了角接触球轴承故障动力学模型，得到了轴承内外圈复合故障的振动信号。采用改进的连续谐波小波包分解方法对复合故障振动信号进行分解和重构，获得了复合故障特征频率，进而重构出与复合故障对应的内外圈单点故障振动信号。通过数值模拟，系统地研究了均方根、峭度和电平通过率与故障尺寸之间的关系，并通过试验进行了验证。结果表明，均方根和电平通过率可以一定程度上定量评估故障尺寸。本文所提出的角接触球轴承内外圈复合故障定量评估方法可以更方便地通过振动信号数据来预测故障尺寸，并监控轴承性能退化规律。